Extra Solved Problem
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Version 7.8-Systemd
Linux From Scratch Version 7.8-systemd Created by Gerard Beekmans Edited by Douglas R. Reno Linux From Scratch: Version 7.8-systemd by Created by Gerard Beekmans and Edited by Douglas R. Reno Copyright © 1999-2015 Gerard Beekmans Copyright © 1999-2015, Gerard Beekmans All rights reserved. This book is licensed under a Creative Commons License. Computer instructions may be extracted from the book under the MIT License. Linux® is a registered trademark of Linus Torvalds. Linux From Scratch - Version 7.8-systemd Table of Contents Preface .......................................................................................................................................................................... vii i. Foreword ............................................................................................................................................................. vii ii. Audience ............................................................................................................................................................ vii iii. LFS Target Architectures ................................................................................................................................ viii iv. LFS and Standards ............................................................................................................................................ ix v. Rationale for Packages in the Book .................................................................................................................... x vi. Prerequisites -

Other Useful Commands
Bioinformatics 101 – Lecture 2 Introduction to command line Alberto Riva ([email protected]), J. Lucas Boatwright ([email protected]) ICBR Bioinformatics Core Computing environments ▪ Standalone application – for local, interactive use; ▪ Command-line – local or remote, interactive use; ▪ Cluster oriented: remote, not interactive, highly parallelizable. Command-line basics ▪ Commands are typed at a prompt. The program that reads your commands and executes them is the shell. ▪ Interaction style originated in the 70s, with the first visual terminals (connections were slow…). ▪ A command consists of a program name followed by options and/or arguments. ▪ Syntax may be obscure and inconsistent (but efficient!). Command-line basics ▪ Example: to view the names of files in the current directory, use the “ls” command (short for “list”) ls plain list ls –l long format (size, permissions, etc) ls –l –t sort newest to oldest ls –l –t –r reverse sort (oldest to newest) ls –lrt options can be combined (in this case) ▪ Command names and options are case sensitive! File System ▪ Unix systems are centered on the file system. Huge tree of directories and subdirectories containing all files. ▪ Everything is a file. Unix provides a lot of commands to operate on files. ▪ File extensions are not necessary, and are not recognized by the system (but may still be useful). ▪ Please do not put spaces in filenames! Permissions ▪ Different privileges and permissions apply to different areas of the filesystem. ▪ Every file has an owner and a group. A user may belong to more than one group. ▪ Permissions specify read, write, and execute privileges for the owner, the group, everyone else. -

Husky: Towards a More Efficient and Expressive Distributed Computing Framework
Husky: Towards a More Efficient and Expressive Distributed Computing Framework Fan Yang Jinfeng Li James Cheng Department of Computer Science and Engineering The Chinese University of Hong Kong ffyang,jfli,[email protected] ABSTRACT tends Spark, and Gelly [3] extends Flink, to expose to programmers Finding efficient, expressive and yet intuitive programming models fine-grained control over the access patterns on vertices and their for data-parallel computing system is an important and open prob- communication patterns. lem. Systems like Hadoop and Spark have been widely adopted Over-simplified functional or declarative programming interfaces for massive data processing, as coarse-grained primitives like map with only coarse-grained primitives also limit the flexibility in de- and reduce are succinct and easy to master. However, sometimes signing efficient distributed algorithms. For instance, there is re- over-simplified API hinders programmers from more fine-grained cent interest in machine learning algorithms that compute by fre- control and designing more efficient algorithms. Developers may quently and asynchronously accessing and mutating global states have to resort to sophisticated domain-specific languages (DSLs), (e.g., some entries in a large global key-value table) in a fine-grained or even low-level layers like MPI, but this raises development cost— manner [14, 19, 24, 30]. It is not clear how to program such algo- learning many mutually exclusive systems prolongs the develop- rithms using only synchronous and coarse-grained operators (e.g., ment schedule, and the use of low-level tools may result in bug- map, reduce, and join), and even with immutable data abstraction prone programming. -
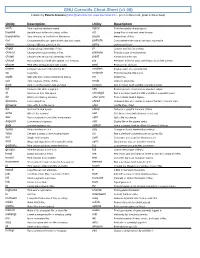
GNU Coreutils Cheat Sheet (V1.00) Created by Peteris Krumins ([email protected], -- Good Coders Code, Great Coders Reuse)
GNU Coreutils Cheat Sheet (v1.00) Created by Peteris Krumins ([email protected], www.catonmat.net -- good coders code, great coders reuse) Utility Description Utility Description arch Print machine hardware name nproc Print the number of processors base64 Base64 encode/decode strings or files od Dump files in octal and other formats basename Strip directory and suffix from file names paste Merge lines of files cat Concatenate files and print on the standard output pathchk Check whether file names are valid or portable chcon Change SELinux context of file pinky Lightweight finger chgrp Change group ownership of files pr Convert text files for printing chmod Change permission modes of files printenv Print all or part of environment chown Change user and group ownership of files printf Format and print data chroot Run command or shell with special root directory ptx Permuted index for GNU, with keywords in their context cksum Print CRC checksum and byte counts pwd Print current directory comm Compare two sorted files line by line readlink Display value of a symbolic link cp Copy files realpath Print the resolved file name csplit Split a file into context-determined pieces rm Delete files cut Remove parts of lines of files rmdir Remove directories date Print or set the system date and time runcon Run command with specified security context dd Convert a file while copying it seq Print sequence of numbers to standard output df Summarize free disk space setuidgid Run a command with the UID and GID of a specified user dir Briefly list directory -

Constraints in Dynamic Symbolic Execution: Bitvectors Or Integers?
Constraints in Dynamic Symbolic Execution: Bitvectors or Integers? Timotej Kapus, Martin Nowack, and Cristian Cadar Imperial College London, UK ft.kapus,m.nowack,[email protected] Abstract. Dynamic symbolic execution is a technique that analyses programs by gathering mathematical constraints along execution paths. To achieve bit-level precision, one must use the theory of bitvectors. However, other theories might achieve higher performance, justifying in some cases the possible loss of precision. In this paper, we explore the impact of using the theory of integers on the precision and performance of dynamic symbolic execution of C programs. In particular, we compare an implementation of the symbolic executor KLEE using a partial solver based on the theory of integers, with a standard implementation of KLEE using a solver based on the theory of bitvectors, both employing the popular SMT solver Z3. To our surprise, our evaluation on a synthetic sort benchmark, the ECA set of Test-Comp 2019 benchmarks, and GNU Coreutils revealed that for most applications the integer solver did not lead to any loss of precision, but the overall performance difference was rarely significant. 1 Introduction Dynamic symbolic execution is a popular program analysis technique that aims to systematically explore all the paths in a program. It has been very successful in bug finding and test case generation [3, 4]. The research community and industry have produced many tools performing symbolic execution, such as CREST [5], FuzzBALL [9], KLEE [2], PEX [14], and SAGE [6], among others. To illustrate how dynamic symbolic execution works, consider the program shown in Figure 1a. -

Operating Systems. Lecture 3
Operating systems. Lecture 3 Michał Goliński 2018-10-16 Introduction Recall • History – Unix – GNU – Linux • bash – man, info – cd – ls, cp, mv etc. Questions? Plan for today • VFS and filesystems overview • processing text Filesystems Empty disk A new disk (hard drive, SSD) is today an array of empty cells called sectors. Sectors are numbered with consecutive numbers. The disk can only read and write one sector at a time. Sectors used to be 512B, but more and more disks use 4kB sectors. ... Historically sectors were addressed by three numbers (cylinder, head and sector) but this is obsolete today. ... 1 Physically there is no empty space – every sector on a brand new disk would give random data when read (at least in principle). Problems To use a disk we need to solve several problems • How to store files and directories? • How to prevent one person from accessing another person’s data? • Which sectors are free and which are taken? ... Files and filesystems are the solution to these problems. Filesystem File is a logical way in which OS handles data on drives. Filesystem (or “file system”)is a logical structure that allows one to write data to disk in an organized way. Most popular filesystems allow to create directory structures, store meta- datada associated with files (ownership, timestamps) and sometimes even error correction in face of hardware errors. A good filesystem should be relatively fast, should not consume too much space in addition to file data and should gracefully handle different errors. Mounting filesystems In order to use a filesystem from a drive it has to be mounted. -

A FIRST COURSE in PROBABILITY This Page Intentionally Left Blank a FIRST COURSE in PROBABILITY
A FIRST COURSE IN PROBABILITY This page intentionally left blank A FIRST COURSE IN PROBABILITY Eighth Edition Sheldon Ross University of Southern California Upper Saddle River, New Jersey 07458 Library of Congress Cataloging-in-Publication Data Ross, Sheldon M. A first course in probability / Sheldon Ross. — 8th ed. p. cm. Includes bibliographical references and index. ISBN-13: 978-0-13-603313-4 ISBN-10: 0-13-603313-X 1. Probabilities—Textbooks. I. Title. QA273.R83 2010 519.2—dc22 2008033720 Editor in Chief, Mathematics and Statistics: Deirdre Lynch Senior Project Editor: Rachel S. Reeve Assistant Editor: Christina Lepre Editorial Assistant: Dana Jones Project Manager: Robert S. Merenoff Associate Managing Editor: Bayani Mendoza de Leon Senior Managing Editor: Linda Mihatov Behrens Senior Operations Supervisor: Diane Peirano Marketing Assistant: Kathleen DeChavez Creative Director: Jayne Conte Art Director/Designer: Bruce Kenselaar AV Project Manager: Thomas Benfatti Compositor: Integra Software Services Pvt. Ltd, Pondicherry, India Cover Image Credit: Getty Images, Inc. © 2010, 2006, 2002, 1998, 1994, 1988, 1984, 1976 by Pearson Education, Inc., Pearson Prentice Hall Pearson Education, Inc. Upper Saddle River, NJ 07458 All rights reserved. No part of this book may be reproduced, in any form or by any means, without permission in writing from the publisher. Pearson Prentice Hall™ is a trademark of Pearson Education, Inc. Printed in the United States of America 10987654321 ISBN-13: 978-0-13-603313-4 ISBN-10: 0-13-603313-X Pearson Education, Ltd., London Pearson Education Australia PTY. Limited, Sydney Pearson Education Singapore, Pte. Ltd Pearson Education North Asia Ltd, Hong Kong Pearson Education Canada, Ltd., Toronto Pearson Educacion´ de Mexico, S.A. -

Gnu Coreutils Core GNU Utilities for Version 6.9, 22 March 2007
gnu Coreutils Core GNU utilities for version 6.9, 22 March 2007 David MacKenzie et al. This manual documents version 6.9 of the gnu core utilities, including the standard pro- grams for text and file manipulation. Copyright c 1994, 1995, 1996, 2000, 2001, 2002, 2003, 2004, 2005, 2006 Free Software Foundation, Inc. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or any later version published by the Free Software Foundation; with no Invariant Sections, with no Front-Cover Texts, and with no Back-Cover Texts. A copy of the license is included in the section entitled \GNU Free Documentation License". Chapter 1: Introduction 1 1 Introduction This manual is a work in progress: many sections make no attempt to explain basic concepts in a way suitable for novices. Thus, if you are interested, please get involved in improving this manual. The entire gnu community will benefit. The gnu utilities documented here are mostly compatible with the POSIX standard. Please report bugs to [email protected]. Remember to include the version number, machine architecture, input files, and any other information needed to reproduce the bug: your input, what you expected, what you got, and why it is wrong. Diffs are welcome, but please include a description of the problem as well, since this is sometimes difficult to infer. See section \Bugs" in Using and Porting GNU CC. This manual was originally derived from the Unix man pages in the distributions, which were written by David MacKenzie and updated by Jim Meyering. -

Verifiable Shuffle of Large Size Ciphertexts
Verifiable Shuffle of Large Size Ciphertexts Jens Groth1? and Steve Lu2 1 UCLA, Computer Science Department [email protected] 2 UCLA, Math Department [email protected] Abstract. A shuffle is a permutation and rerandomization of a set of cipher- texts. Among other things, it can be used to construct mix-nets that are used in anonymization protocols and voting schemes. While shuffling is easy, it is hard for an outsider to verify that a shuffle has been performed correctly. We suggest two efficient honest verifier zero-knowledge (HVZK) arguments for correctness of a shuffle. Our goal is to minimize round-complexity and at the same time have low communicational and computational complexity. The two schemes we suggest are both 3-move HVZK arguments for correctness of a shuffle. We first suggest a HVZK argument based on homomorphic integer commitments, and improve both on round complexity, communication complex- ity and computational complexity in comparison with state of the art. The second HVZK argument is based on homomorphic commitments over finite fields. Here we improve on the computational complexity and communication complexity when shuffling large ciphertexts. Keywords: Shuffle, homomorphic commitment, homomorphic encryption, mix- net, honest verifier zero-knowledge. 1 Introduction The main motivating example for shuffling is mix-nets. Parties can encrypt messages and send them to the mix-net; the mix-net then permutes, decrypts and outputs the messages. This allows parties to submit messages anonymously, which for instance is very useful in voting. One approach to construct a mix-net is the following. The authorities, one by one, permute and rerandomize the ciphertexts. -

TIE: Principled Reverse Engineering of Types in Binary Programs
TIE: Principled Reverse Engineering of Types in Binary Programs JongHyup Lee, Thanassis Avgerinos, and David Brumley Carnegie Mellon University {jonglee, thanassis, dbrumley}@cmu.edu Abstract consider reverse engineering the binary code shown in Fig- ure 1(b) (where source operands come first), compiled from A recurring problem in security is reverse engineering the C code in Figure 1(a). In the first step, variable recov- binary code to recover high-level language data abstrac- ery should infer that (at least) two parameters are passed tions and types. High-level programming languages have and that the function has one local variable. We recover the data abstractions such as buffers, structures, and local vari- information in the typical way by looking at typical access ables that all help programmers and program analyses rea- patterns, e.g., there are two parameters because parameters son about programs in a scalable manner. During compi- are accessed via ebp offsets and there are two unique such lation, these abstractions are removed as code is translated offsets (0xc and 0x8). down to operations on registers and one globally addressed The type recovery task, which gives a high-level type to memory region. Reverse engineering consists of “undoing” each variable, is more challenging. Type recovery is chal- the compilation to recover high-level information so that lenging because high-level types are typically thrown away programmers, security professionals, and analyses can all by the compiler early on in the compilation process. Within more easily reason about the binary code. the compiled code itself we have byte-addressable memory In this paper we develop novel techniques for reverse and registers. -

Introduction to Linux/Unix
Introduction to Linux/Unix Xiaoge Wang, ICER [email protected] Feb. 4, 2016 How does this class work • We are going to cover some basics with hands on examples. • Exercises are denoted by the following icon: • Bold means commands which I expect you type on your terminal in most cases. Green and red sticky Use the sJcKy notes provided to help me help you. – No s%cky = I am worKing – Green = I am done and ready to move on (yea!) – Red = I am stucK and need more Jme and/or some help Agenda • IntroducJon • Linux – Commands • Navigaon • Get or create files • Organizing files • Closer looK into files • Search files • Distribute files • File permission • Learn new commands – Scripts • Pipeline • Make you own command • Environment of a shell • Summary Agenda • Linux – Commands • Navigaon • Get or create files • Organizing files • Closer looK into files • Search files • Distribute files • File permission • Learn new commands – Scripts • Pipeline • Make you own command • Environment of a shell • Summary Introduction • Get ready for adventure? – TicKet(account)? • Big map – Linux/Unix – Shell • Overview of the trail – Commands – Simple Shell script – Get ready for HPC. Exercise 0: Get ready • Connect to HPCC (gateway) – $ ssh [email protected] • Windows users MobaXterm • Mac users Terminal • Linux users? • Read important message – $ mod • Go to a development node – $ ssh dev-nodename Message of the day (mod) • Mac Show screen Big picture Shell Shell Big picture • Shell – CLI ✔ – GUI OS shell example Overview of the trail • Commands • Simple Shell script • Get ready for HPC Linux shell tour Ready? GO! Agenda • IntroducJon – Scripts • Pipeline • Make you own command • Environment of a shell • Summary Example 1: Navigation • TasK: Wander around on a node. -

HR72 / RMS272 CD/MP3 Player
HR72 / RMS272 CD/MP3 Player OWNERS MANUAL Rolls Corporation Salt Lake City, UT 6/06 INTRODUCTION LIMITED WARRANTY Thank you for your purchase of the Rolls RS72/RMS272 CD/MP3 Player. The RS72/RMS272 is a 1/2 rack space CD/MP3 disc Player. Intended mainly for This product is warranted to the original consumer purchaser to be free installation applications, the RS72/RMS272 plays standard audio CDs as well as from defects in materials and workmanship under normal installation, use and CDs formatted with MP3 files. The single rack space height makes it convenient service for a period of one (1) year from the date of purchase as shown on the to install in most any professional audio rack. purchaser’s receipt. FEATURES: • Plays standard CDs as well as discs with MP3 files The obligation of Rolls Corporation under this warranty shall be limited • RCA and 1/8" (3.5 mm) Outputs to repair or replacement (at our option), during the warranty period of any part • Track programming • Repeat All, 1, and Shuffle play which proves defective in material or workmanship under normal installation, • Output Level control use and service, provided the product is returned to Rolls Corporation, TRANS- PORTATION CHARGES PREPAID. Products returned to us or to an authorized INSPECTION Service Center must be accompanied by a copy of the purchase receipt. In the 1. Unpack and Inspect the HR72/RMS272 package Your HR72/RMS272 was carefully packed at the factory in a protective carton. absence of such purchase receipt, the warranty period shall be one (1) year from Nonetheless, be sure to examine the unit and the carton for any signs of damage the date of manufacture.