Neutrinos and the Stars
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Metadata of the Chapter That Will Be Visualized Online
Metadata of the chapter that will be visualized online Chapter Title Binary Systems and Their Nuclear Explosions Copyright Year 2018 Copyright Holder The Author(s) Author Family Name Isern Particle Given Name Jordi Suffix Organization Institute of Space Sciences (ICE, CSIC) Address Barcelona, Spain Organization Institut d’Estudis Espacials de Catalunya (IEEC) Address Barcelona, Spain Email [email protected] Corresponding Author Family Name Hernanz Particle Given Name Margarita Suffix Organization Institute of Space Sciences (ICE, CSIC) Address Barcelona, Spain Organization Institut d’Estudis Espacials de Catalunya (IEEC) Address Barcelona, Spain Email [email protected] Author Family Name José Particle Given Name Jordi Suffix Organization Universitat Politècnica de Catalunya (UPC) Address Barcelona, Spain Organization Institut d’Estudis Espacials de Catalunya (IEEC) Address Barcelona, Spain Email [email protected] Abstract The nuclear energy supply of a typical star like the Sun would be ∼ 1052 erg if all the hydrogen could be incinerated into iron peak elements. Chapter 5 1 Binary Systems and Their Nuclear 2 Explosions 3 Jordi Isern, Margarita Hernanz, and Jordi José 4 5.1 Accretion onto Compact Objects and Thermonuclear 5 Runaways 6 The nuclear energy supply of a typical star like the Sun would be ∼1052 erg if all 7 the hydrogen could be incinerated into iron peak elements. Since the gravitational 8 binding energy is ∼1049 erg, it is evident that the nuclear energy content is more 9 than enough to blow up the Sun. However, stars are stable thanks to the fact that their 10 matter obeys the equation of state of a classical ideal gas that acts as a thermostat: if 11 some energy is released as a consequence of a thermal fluctuation, the gas expands, 12 the temperature drops and the instability is quenched. -

Nobel Lecture: Accelerating Expansion of the Universe Through Observations of Distant Supernovae*
REVIEWS OF MODERN PHYSICS, VOLUME 84, JULY–SEPTEMBER 2012 Nobel Lecture: Accelerating expansion of the Universe through observations of distant supernovae* Brian P. Schmidt (published 13 August 2012) DOI: 10.1103/RevModPhys.84.1151 This is not just a narrative of my own scientific journey, but constant, and suggested that Hubble’s data and Slipher’s also my view of the journey made by cosmology over the data supported this conclusion (Lemaˆitre, 1927). His work, course of the 20th century that has lead to the discovery of the published in a Belgium journal, was not initially widely read, accelerating Universe. It is complete from the perspective of but it did not escape the attention of Einstein who saw the the activities and history that affected me, but I have not tried work at a conference in 1927, and commented to Lemaˆitre, to make it an unbiased account of activities that occurred ‘‘Your calculations are correct, but your grasp of physics is around the world. abominable.’’ (Gaither and Cavazos-Gaither, 2008). 20th Century Cosmological Models: In 1907 Einstein had In 1928, Robertson, at Caltech (just down the road from what he called the ‘‘wonderful thought’’ that inertial accel- Edwin Hubble’s office at the Carnegie Observatories), pre- eration and gravitational acceleration were equivalent. It took dicted the Hubble law, and claimed to see it when he com- Einstein more than 8 years to bring this thought to its fruition, pared Slipher’s redshift versus Hubble’s galaxy brightness his theory of general Relativity (Norton and Norton, 1984)in measurements, but this observation was not substantiated November, 1915. -

Type Ia Supernovaeof Are a the Outc Carbon–Oxygen White Dwarf in a Binary System
Type Ia Supernova: Observations and Theory PoS(NIC XI)066 Jordi Isern∗ Institute for Space Sciences (CSIC-IEEC) E-mail: [email protected] Eduardo Bravo Department of Nuclear Physics (UPC)/IEEC E-mail: [email protected] Alina Hirschmann Institute for Space Sciences (CSIC-IEEC) E-mail: [email protected] There is a wide consensus that Type Ia supernovae are the outcome of the thermonuclear explosion of a carbon–oxygen white dwarf in a binary system. Nevertheless, the nature of this system, the process of ignition itself and the development of the explosion continue to be a mystery despite the important improvements that both, theory and observations, have experienced during the last years. Furthermore, the discovery of new events that are challenging the classical scenario forces the exploration of new issues or, at least, to reconsider scenarios that were rejected at a given moment. 11th Symposium on Nuclei in the Cosmos 19-23 July 2010 Heidelberg, Germany. ∗Speaker. c Copyright owned by the author(s) under the terms of the Creative Commons Attribution-NonCommercial-ShareAlike Licence. http://pos.sissa.it/ Type Ia Supernova: Observations and Theory Jordi Isern 1. Introduction Supernovae are characterized by a sudden rise of their luminosity, by a steep decline after maximum light that lasts several weeks, followed by an exponential decline that can last several years. The total electromagnetic output, obtained from the light curve, is ∼ 1049 erg, while the 10 luminosity at maximum can be as high as ∼ 10 L⊙. The kinetic energy of supernovae can be estimated from the expansion velocity of the ejecta, vexp ∼ 5,000 − 10,000 km/s, and turns out to be ∼ 1051 erg. -

Aleksandar Cikota Astromundus Programme
A STUDY OF THE EFFECT OF HOST GALAXY EXTINCTION ON THE COLORS OF TYPE IA SUPERNOVAE Aleksandar Cikota Submitted to the INSTITUTE FOR ASTRO- AND PARTICLE PHYSICS of the UNIVERSITY OF INNSBRUCK AstroMundus Programme in Partial Fulfillment of the Requirements for the Degree of MAGISTER DER NATURWISSENSCHAFTEN (Master of Science, MSc) in Astronomy & Astrophysics Supervised by: Assoc. Prof. Francine Marleau, Univ. Prof. Dr. Norbert Przybilla Innsbruck, July 2015 Preface The reserch for this Master’s thesis was partially conducted at the Space Telescope Sci- ence Institute in Balimore, MD, USA, during a 15 weeks internship hosted by Dr. Susana Deustua. Also, a manuscript containing the research conducted for this master thesis, enti- tled ”Determining Type Ia Supernovae host galaxy extinction probabilities and a statistical approach to estimating the absorption-to-reddening ratio RV ” by Aleksandar Cikota, Su- sana Deustua, and Francine Marleau, was submitted to The Astrophysical Journal on May 13th, 2015. Aleksandar Cikota Baltimore, June 2015 i Abstract We aim to place limits on the extinction values of Type Ia supernovae to statistically de- termine the most probable color excess, E(B-V), with galactocentric distance, and to use these statistics to determine the absorption-to-reddening ratio, RV , for dust in the host galaxies. We determined pixel-based dust mass surface density maps for 59 galaxies from the Key Insight on Nearby Galaxies: a Far-Infrared Survey with Herschel (KINGFISH, Ken- nicutt et al. (2011)). We use Type Ia supernova spectral templates (Hsiao et al., 2007) to develop a Monte Carlo simulation of color excess E(B-V) with RV =3.1 and investigate the color excess probabilities E(B-V) with projected radial galaxy center distance. -

Cycle 20 Abstract Catalog (Based on Phase I Submissions)
Cycle 20 Abstract Catalog (Based on Phase I Submissions) Proposal Category: AR Scientific Category: STAR FORMATION ID: 12814 Program Title: Signatures of turbulence in directly imaged protoplanetary disks Principal Investigator: Philip Armitage PI Institution: University of Colorado at Boulder HST imaging of the edge-on protoplanetary disk in the HH 30 system has shown that substantial changes to the morphology of the disk occur on time scales much shorter than the local dynamical time. This may be due to time- variable obscuration of starlight by the turbulent inner disk. More recently, mid-infrared variability of protoplanetary disks has been attributed to a similar physical origin. We propose a theoretical investigation that will establish whether the optical and infrared variability is due to turbulent variations in the scale height of dust in the inner disk, and determine what observations of that variability can tell us of the nature of disk turbulence. We will use a new generation of global magnetohydrodynamic simulations to directly model the turbulence in an annulus of the inner disk, extending from the dust destruction radius out to the radius where turbulence is quenched by poor coupling of the gas to magnetic fields. We will use the output of the MHD simulations as input to Monte Carlo radiative transfer calculations of stellar irradiation of the outer disk. We will use these calculations to produce light curves that show how time variable shadowing from the inner disk affects the outer disk observables: scattered light images and the infrared spectral energy distribution. Proposal Category: GO Scientific Category: COOL STARS ID: 12815 Program Title: Photometry of the Coldest Benchmark Brown Dwarf Principal Investigator: Kevin Luhman PI Institution: The Pennsylvania State University In 2011, we used images from the Spitzer Space Telescope to discover the coldest directly imaged companion to a nearby star (300-345 K). -

Supernovae Seen Through Gravitational Telescopes
Supernovae seen through gravitational telescopes Tanja Petrushevska Academic dissertation for the Degree of Doctor of Philosophy in Physics at Stockholm University to be publicly defended on Monday 29 May 2017 at 10.15 in sal FB42, AlbaNova universitetscentrum, Roslagstullsbacken 21. Abstract Galaxies, and clusters of galaxies, can act as gravitational lenses and magnify the light of objects behind them. The effect enables observations of very distant supernovae, that otherwise would be too faint to be detected by existing telescopes, and allows studies of the frequency and properties of these rare phenomena when the universe was young. Under the right circumstances, multiple images of the lensed supernovae can be observed, and due to the variable nature of the objects, the difference between the arrival times of the images can be measured. Since the images have taken different paths through space before reaching us, the time-differences are sensitive to the expansion rate of the universe. One class of supernovae, Type Ia, are of particular interest to detect. Their well known brightness can be used to determine the magnification, which can be used to understand the lensing systems. In this thesis, galaxy clusters are used as gravitational telescopes to search for lensed supernovae at high redshift. Ground- based, near-infrared and optical search campaigns are described of the massive clusters Abell 1689 and 370, which are among the most powerful gravitational telescopes known. The search resulted in the discovery of five photometrically classified, core-collapse supernovae at redshifts of 0.671<z<1.703 with significant magnification from the cluster. Owing to the power of the lensing cluster, the volumetric core-collapse supernova rates for 0.4 ≤ z < 2.9 were calculated, and found to be in good agreement with previous estimates and predictions from cosmic star formation history. -
Stsci Newsletter: 2017 Volume 034 Issue 02
2017 - Volume 34 - Issue 02 Emerging Technologies: Bringing the James Webb Space Telescope to the World Like the rest of the Institute, excitement is building in the Office of Public Outreach (OPO) as the clock winds down for the launch of the James Webb Space Telescope. Our task is translating and sharing this excitement over groundbreaking engineering—and the scientific discoveries to come—with the public. Webb @ STScI In the lead-up to Webb’s launch in Spring 2019, the Institute continues its work as the science and operations center for the mission. The Institute has played a critical role in a number of recent Webb mission milestones. Updates on Hubble Operation at the Institute Observations with the Hubble Space Telescope continue to be in great demand. This article discusses Cycle 24 observing programs and scheduling efficiency, maintaining COS productivity into the next decade, keeping Hubble operations smooth and efficient, and ensuring the freshness of Hubble archive data. Hubble Cycle 25 Proposal Selection Hubble is in high demand and continues to add to our understanding of the universe. The peer-review proposal selection process plays a fundamental role in establishing a merit-based science program, and that is only possible thanks to the work and integrity of all the Time Allocation Committee (TAC) and review panel members, and the external reviewers. We present here the highlights of the Cycle 25 selection process. Using Gravity to Measure the Mass of a Star In a reprise of the famous 1919 solar eclipse experiment that confirmed Einstein's general relativity, the nearby white dwarf, Stein 2051 B, passed very close to a background star in March 2014. -

Nuclear Outbursts in the Centers of Galaxies
Nuclear Outbursts in the Centers of Galaxies A dissertation presented to the faculty of the College of Arts and Sciences of Ohio University In partial fulfillment of the requirements for the degree Doctor of Philosophy Reza Katebi December 2019 © 2019 Reza Katebi. All Rights Reserved. 2 This dissertation titled Nuclear Outbursts in the Centers of Galaxies by REZA KATEBI has been approved for the Department of Physics and Astronomy and the College of Arts and Sciences by Ryan Chornock Assistant Professor of Physics and Astronomy Florenz Plassmann Dean, College of Arts and Sciences 3 Abstract KATEBI, REZA, Ph.D., December 2019, Physics Nuclear Outbursts in the Centers of Galaxies (182 pp.) Director of Dissertation: Ryan Chornock This dissertation consists of two parts. In the first part, we focus on studying the nuclear outbursts in the centers of galaxies and their nature in order to better understand the behavior of central Super Massive Black Holes (SMBHs) and their interaction with the surrounding environment, and to better understand the accretion disk structure. Nuclear outbursts can be better understood by studying the changes in the broad emission lines and the underlying continuum. We quantify the properties of these nuclear outbursts using multi-wavelength observations including optical, ultraviolet, and X-rays from MDM Observatory, the Sloan Digital Sky Survey, Swift, and Magellan. Some of these nuclear outbursts are linked to Tidal Disruption Events (TDEs) and nuclear supernovae (SNs), while a number of these events are proposed to be a rare phenomenon called “changing-look” Active Galactic Nuclei (AGN). These types of AGNs have been observed to optically transition from type 1 to type 2 and vice versa on timescales of months to years, where broad emission lines such as Hα and Hβ appeared or disappeared followed by an increase or decrease in the continuum light. -

Pushing the Helium Envelope: Signatures of Normal and Unusual Supernovae from Sub-Chandrasekhar Mass White Dwarf Explosions
Pushing the Helium Envelope: Signatures of Normal and Unusual Supernovae from Sub-Chandrasekhar Mass White Dwarf Explosions by Abigail E. Polin A dissertation submitted in partial satisfaction of the requirements for the degree of Doctor of Philosophy in Physics in the Graduate Division of the University of California, Berkeley Committee in charge: Dr. Peter Nugent, Co-chair Associate Professor Daniel Kasen, Co-chair Professor Christopher McKee Professor Alexei V. Filippenko Spring 2020 Pushing the Helium Envelope: Signatures of Normal and Unusual Supernovae from Sub-Chandrasekhar Mass White Dwarf Explosions Copyright 2020 by Abigail E. Polin 1 Abstract Pushing the Helium Envelope: Signatures of Normal and Unusual Supernovae from Sub-Chandrasekhar Mass White Dwarf Explosions by Abigail E. Polin Doctor of Philosophy in Physics University of California, Berkeley Dr. Peter Nugent, Co-chair Associate Professor Daniel Kasen, Co-chair Type Ia supernovae (SNe) are among the most common astrophysical transients, yet their progenitors are still unknown. Throughout this thesis we examine a specific pathway to these explosions – the double detonation explosion mechanism. In this scenario a white dwarf (WD) is able to explode below the Chandrasekhar mass limit through the aid of an accreted helium shell. An ignition of this helium can send a shock wave into the center of the WD which, upon convergence, can ignite the core causing a thermonuclear runaway resulting in a Type Ia-like explosion. Prior to this work, the double detonation scenario was not favored as a mechanism for Type Ia SNe, as there was no strong observational evidence supporting it. The first part of this thesis is a calculation of observational predictions of double detonation explosions. -

Quark-Novae Ia in the Hubble Diagram: Implications for Dark Energy 3
Research in Astron. Astrophys. Vol.0 (200x) No.0, 000–000 Research in http://www.raa-journal.org http://www.iop.org/journals/raa Astronomy and Astrophysics Quark-Novae Ia in the Hubble diagram: Implications For Dark Energy Rachid Ouyed1, Nico Koning1, Denis Leahy1, Jan E. Staff2 and Daniel T. Cassidy3 1 Department of Physics and Astronomy, University of Calgary, 2500 University Drive NW, Calgary, Alberta, T2N 1N4 Canada; [email protected] 2 Department of Physics and Astronomy, Macquarie University NSW 2109, Australia 3 Department of Engineering Physics, McMaster University, Hamilton, Ontario, Canada L8S 4L7 Abstract The accelerated expansion of the Universe was proposed through the use of Type-Ia SNe as standard candles. The standardization depends on an empirical correlation between the stretch/color and peak luminosity of the light curves. The use of Type Ia SN as standard candles rests on the assumption that their properties (and this correlation) do not vary with red-shift. We consider the possibility that the majority of Type-Ia SNe are in fact caused by a Quark-Nova detonation in a tight neutron-star-CO-white- dwarf binary system; a Quark-Nova Ia. The spin-down energy injected by the Quark Nova remnant (the quark star) contributes to the post-peak light curve and neatly explains the observed correlation between peak luminosity and light curve shape. We demonstrate that the parameters describing Quark-Novae Ia are NOT constant in red-shift. Simulated Quark-Nova Ia light curves provide a test of the stretch/color correlation by comparing the true distance modulus with that determined using SN light curve fitters. -
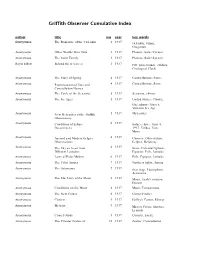
Griffith Observer Cumulative Index
Griffith Observer Cumulative Index author title mo year key words Anonymous The Romance of the Calendar 2 1937 calendar, Julian, Gregorian Anonymous Other Worlds than Ours 3 1937 Planets, Solar System Anonymous The S ola r Fa mily 3 1937 Planets, Solar System Roya l Elliott Behind the Sciences 3 1937 GO, pla ne ta rium, e xhibits , Ge ologica l Clock Anonymous The Stars of Spring 4 1937 Cons te lla tions , S ta rs , Anonymous Pronunciation of Star and 4 1937 Cons te lla tions , S ta rs Constellation Names Anonymous The Cycle of the Seasons 5 1937 Seasons, climate Anonymous The Ice Ages 5 1937 United States, Climate, Greenhouse Gases, Volcano, Ice Age Anonymous New Meteorites at the Griffith 5 1937 Meteorites Observatory Anonymous Conditions of Eclipse 6 1937 Solar eclipse, June 8, Occurrences 1937, Umbra, Sun, Moon Anonymous Ancient and Modern Eclipse 6 1937 Chinese, Observation, Observations Eclips e , Re la tivity Anonymous The Sky as Seen from 6 1937 Stars, Celestial Sphere, Different Latitudes Equator, Pole, Latitude Anonymous Laws of Polar Motion 6 1937 Pole, Equator, Latitude Anonymous The Polar Aurora 7 1937 Northern lights, Aurora Anonymous The Astrorama 7 1937 Star map, Planisphere, Astrorama Anonymous The Life Story of the Moon 8 1937 Moon, Earth's rotation, Darwin Anonymous Conditions on the Moon 8 1937 Moon, Temperature, Anonymous The New Comet 8 1937 Come t Fins le r Anonymous Comets 9 1937 Halley's Comet, Meteor Anonymous Meteors 9 1937 Meteor Crater, Shower, Leonids Anonymous Comet Orbits 9 1937 Comets, Encke Anonymous -
![Arxiv:1902.01433V1 [Astro-Ph.CO] 4 Feb 2019 Between Supernova Color and Peak Luminosity Was Also Shown to Improve Distance Estimates of Snia (Riess Et Al](https://docslib.b-cdn.net/cover/2691/arxiv-1902-01433v1-astro-ph-co-4-feb-2019-between-supernova-color-and-peak-luminosity-was-also-shown-to-improve-distance-estimates-of-snia-riess-et-al-5382691.webp)
Arxiv:1902.01433V1 [Astro-Ph.CO] 4 Feb 2019 Between Supernova Color and Peak Luminosity Was Also Shown to Improve Distance Estimates of Snia (Riess Et Al
Draft version February 6, 2019 Typeset using LATEX twocolumn style in AASTeX62 Think Global, Act Local: The Influence of Environment Age and Host Mass on Type Ia Supernova Light Curves B. M. Rose,1 P. M. Garnavich,1 and M. A. Berg1 1University of Notre Dame, Center for Astrophysics, Notre Dame, IN 46556 (Dated: February 6, 2019; Received November 12, 2018; Revised January 29, 2019; Accepted February 4, 2019) Submitted to ApJ ABSTRACT The reliability of Type Ia supernovae (SNIa) may be limited by the imprint of their galactic origins. To investigate the connection between supernovae and their host characteristics, we developed an improved method to estimate the stellar population age of the host as well as the local environment around the site of the supernova. We use a Bayesian method to estimate the star formation history and mass weighted age of a supernova's environment by matching observed spectral energy distributions to a synthesized stellar population. Applying this age estimator to both the photometrically and spectroscopically classified Sloan Digital Sky Survey II supernovae (N=103) we find a 0:114±0:039 mag \step" in the average Hubble residual at a stellar age of ∼ 8 Gyr; it is nearly twice the size of the currently popular mass step. We then apply a principal component analysis on the SALT2 parameters, host stellar mass, and local environment age. We find that a new parameter, PC1, consisting of a linear combination of stretch, host stellar mass, and local age, shows a very significant (4:7σ) correlation with Hubble residuals. There is a much broader range of PC1 values found in the Hubble flow sample when compared with the Cepheid calibration galaxies.