A Pilot-Wave Gravity and the Titius-Bode Law
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Messier Objects
Messier Objects From the Stocker Astroscience Center at Florida International University Miami Florida The Messier Project Main contributors: • Daniel Puentes • Steven Revesz • Bobby Martinez Charles Messier • Gabriel Salazar • Riya Gandhi • Dr. James Webb – Director, Stocker Astroscience center • All images reduced and combined using MIRA image processing software. (Mirametrics) What are Messier Objects? • Messier objects are a list of astronomical sources compiled by Charles Messier, an 18th and early 19th century astronomer. He created a list of distracting objects to avoid while comet hunting. This list now contains over 110 objects, many of which are the most famous astronomical bodies known. The list contains planetary nebula, star clusters, and other galaxies. - Bobby Martinez The Telescope The telescope used to take these images is an Astronomical Consultants and Equipment (ACE) 24- inch (0.61-meter) Ritchey-Chretien reflecting telescope. It has a focal ratio of F6.2 and is supported on a structure independent of the building that houses it. It is equipped with a Finger Lakes 1kx1k CCD camera cooled to -30o C at the Cassegrain focus. It is equipped with dual filter wheels, the first containing UBVRI scientific filters and the second RGBL color filters. Messier 1 Found 6,500 light years away in the constellation of Taurus, the Crab Nebula (known as M1) is a supernova remnant. The original supernova that formed the crab nebula was observed by Chinese, Japanese and Arab astronomers in 1054 AD as an incredibly bright “Guest star” which was visible for over twenty-two months. The supernova that produced the Crab Nebula is thought to have been an evolved star roughly ten times more massive than the Sun. -

Chapter Two: the Astronomers and Extraterrestrials
Warning Concerning Copyright Restrictions The Copyright Law of the United States (Title 17, United States Code) governs the making of photocopies or other reproductions of copyrighted materials, Under certain conditions specified in the law, libraries and archives are authorized to furnish a photocopy or other reproduction, One of these specified conditions is that the photocopy or reproduction is not to be used for any purpose other than private study, scholarship, or research , If electronic transmission of reserve material is used for purposes in excess of what constitutes "fair use," that user may be liable for copyright infringement. • THE EXTRATERRESTRIAL LIFE DEBATE 1750-1900 The idea of a plurality of worlds from Kant to Lowell J MICHAEL]. CROWE University of Notre Dame TII~ right 0/ ,It, U,,;v"Jily 0/ Camb,idg4' to P'''''' a"d s,1I all MO""" of oooks WM grattlrd by H,rr,y Vlf(;ff I $J4. TM U,wNn;fyltas pritr"d and pu"fisllrd rOffti",.ously sincr J5U. Cambridge University Press Cambridge London New York New Rochelle Melbourne Sydney Published by the Press Syndicate of the University of Cambridge In lovi ng The Pirr Building, Trumpingron Srreer, Cambridge CB2. I RP Claire H 32. Easr 57th Streer, New York, NY 1002.2., U SA J 0 Sramford Road, Oakleigh, Melbourne 3166, Australia and Mi ha © Cambridge Univ ersiry Press 1986 firsr published 1986 Prinred in rh e Unired Srares of America Library of Congress Cataloging in Publication Data Crowe, Michael J. The exrrarerresrriallife debare '750-1900. Bibliography: p. Includes index. I. Pluraliry of worlds - Hisrory. -

The Midnight Sky: Familiar Notes on the Stars and Planets, Edward Durkin, July 15, 1869 a Good Way to Start – Find North
The expression "dog days" refers to the period from July 3 through Aug. 11 when our brightest night star, SIRIUS (aka the dog star), rises in conjunction* with the sun. Conjunction, in astronomy, is defined as the apparent meeting or passing of two celestial bodies. TAAS Fabulous Fifty A program for those new to astronomy Friday Evening, July 20, 2018, 8:00 pm All TAAS and other new and not so new astronomers are welcome. What is the TAAS Fabulous 50 Program? It is a set of 4 meetings spread across a calendar year in which a beginner to astronomy learns to locate 50 of the most prominent night sky objects visible to the naked eye. These include stars, constellations, asterisms, and Messier objects. Methodology 1. Meeting dates for each season in year 2018 Winter Jan 19 Spring Apr 20 Summer Jul 20 Fall Oct 19 2. Locate the brightest and easiest to observe stars and associated constellations 3. Add new prominent constellations for each season Tonight’s Schedule 8:00 pm – We meet inside for a slide presentation overview of the Summer sky. 8:40 pm – View night sky outside The Midnight Sky: Familiar Notes on the Stars and Planets, Edward Durkin, July 15, 1869 A Good Way to Start – Find North Polaris North Star Polaris is about the 50th brightest star. It appears isolated making it easy to identify. Circumpolar Stars Polaris Horizon Line Albuquerque -- 35° N Circumpolar Stars Capella the Goat Star AS THE WORLD TURNS The Circle of Perpetual Apparition for Albuquerque Deneb 1 URSA MINOR 2 3 2 URSA MAJOR & Vega BIG DIPPER 1 3 Draco 4 Camelopardalis 6 4 Deneb 5 CASSIOPEIA 5 6 Cepheus Capella the Goat Star 2 3 1 Draco Ursa Minor Ursa Major 6 Camelopardalis 4 Cassiopeia 5 Cepheus Clock and Calendar A single map of the stars can show the places of the stars at different hours and months of the year in consequence of the earth’s two primary movements: Daily Clock The rotation of the earth on it's own axis amounts to 360 degrees in 24 hours, or 15 degrees per hour (360/24). -

Remembering Bill Bogardus Photographing the Moon
Published by the Astronomical League Vol. 71, No. 2 March 2019 REMEMBERING BILL BOGARDUS PHOTOGRAPHING THE MOON 7.20.69 5 YEARS TREASURES OF THE LINDA HALL LIBRARY APOLLO 11 THE COSMIC WEB ONOMY T STR O T A H G E N P I E Contents G O N P I L R E B 4 . Reflector Mail ASTRONOMY DAY Join a Tour This Year! 4 . President’s Corner May 11 & 5 . International Dark-Sky Association From 37,000 feet above the Pacific Total Eclipse Flight: Chile October 5, 2019 6 . Night Sky Network Ocean, you’ll be high above any clouds, July 2, 2019 For a FREE 76-page seeing up to 3¼ minutes of totality in a dark sky that makes the Sun’s corona look 6 . Deep-Sky Objects Astronomy Day Handbook incredibly dramatic. Our flight will de- full of ideas and suggestions, part from and return to Santiago, Chile. 9 . Remembering Bill Bogardus skyandtelescope.com/2019eclipseflight go to: 10 . From Around the League www.astroleague.org Click on "Astronomy Day” African Stargazing Safari Join astronomer Stephen James PAGE 19 13 . Observing Awards Scroll down to "Free O’Meara in wildlife-rich Botswana July 29–August 4, 2019 Astronomy Day Handbook" for evening stargazing and daytime 14 . Basic Small-Scope Lunar Imaging safari drives at three luxury field For more information, contact: camps. Only 16 spaces available! 18 . The Vault of Heaven – Gary Tomlinson Optional extension to Victoria Falls. ̨̨̨̨̨̨̨̨̨̨̨̨̨̨̨Treasures of the Linda Hall Library Astronomy Day Coordinator skyandtelescope.com/botswana2019 [email protected] 24 . The Cosmic Web Iceland Aurorae 27 . -

Self-Organizing Systems in Planetary Physics: Harmonic Resonances Of
Self-Organizing Systems in Planetary Physics : Harmonic Resonances of Planet and Moon Orbits Markus J. Aschwanden1 1) Lockheed Martin, Solar and Astrophysics Laboratory, Org. A021S, Bldg. 252, 3251 Hanover St., Palo Alto, CA 94304, USA; e-mail: [email protected] ABSTRACT The geometric arrangement of planet and moon orbits into a regularly spaced pattern of distances is the result of a self-organizing system. The positive feedback mechanism that operates a self-organizing system is accomplished by harmonic orbit resonances, leading to long-term stable planet and moon orbits in solar or stellar systems. The distance pattern of planets was originally described by the empirical Titius-Bode law, and by a generalized version with a constant geometric progression factor (corresponding to logarithmic spacing). We find that the orbital periods Ti and planet distances Ri from the Sun are not consistent with logarithmic spacing, 2/3 2/3 but rather follow the quantized scaling (Ri+1/Ri) = (Ti+1/Ti) = (Hi+1/Hi) , where the harmonic ratios are given by five dominant resonances, namely (Hi+1 : Hi)=(3:2), (5 : 3), (2 : 1), (5 : 2), (3 : 1). We find that the orbital period ratios tend to follow the quantized harmonic ratios in increasing order. We apply this harmonic orbit resonance model to the planets and moons in our solar system, and to the exo-planets of 55 Cnc and HD 10180 planetary systems. The model allows us a prediction of missing planets in each planetary system, based on the quasi- regular self-organizing pattern of harmonic orbit resonance zones. We predict 7 (and 4) missing exo-planets around the star 55 Cnc (and HD 10180). -

The Astronomical Work of Carl Friedrich Gauss
View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Elsevier - Publisher Connector HISTORIA MATHEMATICA 5 (1978), 167-181 THE ASTRONOMICALWORK OF CARL FRIEDRICH GAUSS(17774855) BY ERIC G, FORBES, UNIVERSITY OF EDINBURGH, EDINBURGH EH8 9JY This paper was presented on 3 June 1977 at the Royal Society of Canada's Gauss Symposium at the Ontario Science Centre in Toronto [lj. SUMMARIES Gauss's interest in astronomy dates from his student-days in Gattingen, and was stimulated by his reading of Franz Xavier von Zach's Monatliche Correspondenz... where he first read about Giuseppe Piazzi's discovery of the minor planet Ceres on 1 January 1801. He quickly produced a theory of orbital motion which enabled that faint star-like object to be rediscovered by von Zach and others after it emerged from the rays of the Sun. Von Zach continued to supply him with the observations of contemporary European astronomers from which he was able to improve his theory to such an extent that he could detect the effects of planetary perturbations in distorting the orbit from an elliptical form. To cope with the complexities which these introduced into the calculations of Ceres and more especially the other minor planet Pallas, discovered by Wilhelm Olbers in 1802, Gauss developed a new and more rigorous numerical approach by making use of his mathematical theory of interpolation and his method of least-squares analysis, which was embodied in his famous Theoria motus of 1809. His laborious researches on the theory of Pallas's motion, in whi::h he enlisted the help of several former students, provided the framework of a new mathematical formu- lation of the problem whose solution can now be easily effected thanks to modern computational techniques. -

Caput Medusae
john c. barentine ASTERISMS, SINGLE-SOURCE AND REBRANDS Uncharted Constellations Asterisms, Single-Source and Rebrands John C. Barentine Uncharted Constellations Asterisms, Single-Source and Rebrands 123 John C. Barentine TUCSON, AZ, USA SPRINGER PRAXIS BOOKS IN POPULAR ASTRONOMY Springer Praxis Books ISBN 978-3-319-27618-2 ISBN 978-3-319-27619-9 (eBook) DOI 10.1007/978-3-319-27619-9 Library of Congress Control Number: 2015958891 Springer Cham Heidelberg New York Dordrecht London © Springer International Publishing Switzerland 2016 This work is subject to copyright. All rights are reserved by the Publisher, whether the whole or part of the material is concerned, specifically the rights of translation, reprinting, reuse of illustrations, recitation, broadcasting, reproduction on microfilms or in any other physical way, and transmission or information storage and retrieval, electronic adaptation, computer software, or by similar or dissimilar methodology now known or hereafter developed. The use of general descriptive names, registered names, trademarks, service marks, etc. in this publication does not imply, even in the absence of a specific statement, that such names are exempt from the relevant protective laws and regulations and therefore free for general use. The publisher, the authors and the editors are safe to assume that the advice and information in this book are believed to be true and accurate at the date of publication. Neither the publisher nor the authors or the editors give a warranty, express or implied, with respect to the material contained herein or for any errors or omissions that may have been made. Cover illustration: “Lacerta, Cygnus, Lyra, Vulpecula and Anser”, plate 14 in Urania’s Mirror, a set of celestial cards accompanied by A familiar treatise on astronomy...byJehoshaphatAspin.London. -

Barry Lawrence Ruderman Antique Maps Inc
Barry Lawrence Ruderman Antique Maps Inc. 7407 La Jolla Boulevard www.raremaps.com (858) 551-8500 La Jolla, CA 92037 [email protected] Orion and Haase (Lepus the Rabbit) Stock#: 56255 Map Maker: Bode Date: 1805 Place: Berlin Color: Hand Colored Condition: VG+ Size: 9 x 7 inches Price: SOLD Description: Striking star chart centered the constellations Orion and Lepus, published by Johann Elert Bode (1747-1826), in his Vorstellung der Gestirne auf XXXIV Tafeln, 1805. Shows the featured constellations in color with neighboring stars and constellations without color or in much lighter colors. Bode was born in Hamburg. His first publication was on the solar eclipse, August 5, 1766. This was followed by an elementary treatise on astronomy entitled Anleitung zur Kenntniss des gestirnten Himmels, the success of which led to his being summoned to Berlin in 1772 for the purpose of computing ephemerides on an improved plan. In 1774, Bode started the well-known Astronomisches Jahrbuch, a journal which ran to 51 yearly volumes. Bode became director of the Berlin Observatory in 1786, where he remained until 1825. There he published the Uranographia in 1801, a celestial atlas that aimed both at scientific accuracy in showing the positions of stars and other astronomical objects, as well as the artistic interpretation of the stellar constellation figures. The Uranographia marks the climax of an epoch of artistic representation of the constellations. Later atlases showed fewer and fewer elaborate figures until they were no longer printed on such tables. Bode also published a small star atlas, intended for astronomical amateurs ( Vorstellung der Gestirne). -

The Milky Way the Milky Way's Neighbourhood
The Milky Way What Is The Milky Way Galaxy? The.Milky.Way.is.the.galaxy.we.live.in..It.contains.the.Sun.and.at.least.one.hundred.billion.other.stars..Some.modern. measurements.suggest.there.may.be.up.to.500.billion.stars.in.the.galaxy..The.Milky.Way.also.contains.more.than.a.billion. solar.masses’.worth.of.free-floating.clouds.of.interstellar.gas.sprinkled.with.dust,.and.several.hundred.star.clusters.that. contain.anywhere.from.a.few.hundred.to.a.few.million.stars.each. What Kind Of Galaxy Is The Milky Way? Figuring.out.the.shape.of.the.Milky.Way.is,.for.us,.somewhat.like.a.fish.trying.to.figure.out.the.shape.of.the.ocean.. Based.on.careful.observations.and.calculations,.though,.it.appears.that.the.Milky.Way.is.a.barred.spiral.galaxy,.probably. classified.as.a.SBb.or.SBc.on.the.Hubble.tuning.fork.diagram. Where Is The Milky Way In Our Universe’! The.Milky.Way.sits.on.the.outskirts.of.the.Virgo.supercluster..(The.centre.of.the.Virgo.cluster,.the.largest.concentrated. collection.of.matter.in.the.supercluster,.is.about.50.million.light-years.away.).In.a.larger.sense,.the.Milky.Way.is.at.the. centre.of.the.observable.universe..This.is.of.course.nothing.special,.since,.on.the.largest.size.scales,.every.point.in.space. is.expanding.away.from.every.other.point;.every.object.in.the.cosmos.is.at.the.centre.of.its.own.observable.universe.. Within The Milky Way Galaxy, Where Is Earth Located’? Earth.orbits.the.Sun,.which.is.situated.in.the.Orion.Arm,.one.of.the.Milky.Way’s.66.spiral.arms..(Even.though.the.spiral. -

Aerospace Engineering Uranus
Virtual Learning Aerospace Engineering Uranus May 13, 2020 Aerospace Engineering Lesson: May 13, 2020 Objective/Learning Target: Students will learn about Uranus by exploring various aspects of planet. Bell Work: How far away is Uranus from Earth? 3 Let’s Get Started: Watch Videos: ● Uranus 101 | National Geographic ● Uranus & Neptune: Crash Course Astronomy #19 4 Uranus 5 6 Uranus is the seventh planet from the Sun and has the third largest diameter in our solar system. Uranus is very cold and windy. It is surrounded by 13 faint rings and 27 small moons as it rotates at a nearly 90-degree angle from the plane of its orbit. This unique tilt makes Uranus appear to spin on its side, orbiting the Sun like a rolling ball. Uranus was the first planet found with the aid of a telescope, it was discovered in 1781 by astronomer William Herschel, although he originally thought it was either a comet or a star. It was two years later that Uranus was universally accepted as a new planet, because of observations by astronomer Johann Elert Bode. William Herschel tried unsuccessfully to name his discovery Georgium Sidus after King George III. Instead the planet was named for Uranus, after the Greek god of the sky, as requested by Johann Bode. 7 Uranus has a radius of 15,759.2 miles and is 4 times wider than Earth. Uranus is 19.8 astronomical units (AU) away from the Sun. One astronomical unit is the distance from the Sun to Earth. It takes sunlight 2 hours and 40 minutes to travel from the Sun to Uranus. -
Reflections the Titius-Bode Rule, Part 2: Science Or Numerology?
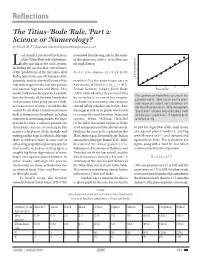
Reflections The Titius-Bode Rule, Part 2: Science or Numerology? by David M. F. Chapman ([email protected]) ast month, I presented the history postulated the following rule for the radius of the Titius-Bode rule of planetary of the planetary orbits: from Mercury Lorbit spacing in the solar system, through Saturn, including the spectacular concordance of the “predictions” of the rule (also called D = 0.4 + 0.3 n, where n = {0, 1, 2, 4, 8, 16, 32} Bode’s law) in the case of Uranus and the asteroids, and the abysmal failure of the in which D is the semi-major axis in rule with respect to the last two planets Astronomical Units (i.e. DEarth=1 AU). discovered: Neptune and Pluto. This Fellow German Johann Elert Bode month, I will review the quest for a scientific (1747–1826) liked the idea so much that The approximate logarithmic spacing of the basis to this rule. At the time I made this he included it in one of his popular planetary orbits. Filled circles are the exact rash promise, I was going out on a limb, textbooks on astronomy, and everyone semi-major axis values; open diamonds are as I was unsure of what I would be able started calling it Bode’s Law. In fact, there the Titius-Bode law results. Note the excellent to find. To my relief, I found an extensive was a gap at n=8, as no planet was known “predictions” of Ceres (k=5) and Uranus (k=8) body of literature on the subject, including to occupy the zone between Mars and and the poor “predictions” of Neptune (k=9) some recent interesting studies. -

Star Tales 2018
CHAPTER ONE Stars and storytellers VERY NIGHT a pageant of Greek mythology circles overhead. Perseus flies to the rescue of Andromeda, Orion faces the charge of the snorting Ebull, Boötes herds the bears around the pole, and the ship of the Argo - nauts sails in search of the golden fleece. These legends, along with many others, are depicted in the star patterns that astronomers term constellations. Constellations are the invention of human imagination, not of nature. They are an expression of the human desire to impress its own order upon the appar- ent chaos of the night sky. For navigators beyond sight of land or for travellers in the trackless desert who wanted signposts, for farmers who wanted a calendar and for shepherds who wanted a nightly clock, the division of the sky into recognizable star groupings had practical purposes. But perhaps the earliest motivation was to humanize the forbidding blackness of night. Newcomers to astronomy are soon disappointed to find that the great majority of constellations bear little, if any, resemblance to the figures whose names they carry; but to expect such a resemblance is to misunderstand their true meaning. The constellation figures are not intended to be taken literally. Rather, they are symbolic, a celestial allegory. The night sky was a screen on which human imaginationSAMPLE could project the deeds and personifications of deities, sacred animals, and moral tales. It was a picture book in the days before writing. Each evening the stars emerge like magic spirits as the Sun descends to its nocturnal lair. Modern science has told us that those twinkling points scattered across the sky are actually glowing balls of gas similar to our own Sun, immensely far away.