Identification of Putative Causal Loci in Whole-Genome
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Genetic and Epigenetic Variation in the Human Genome
Digital Comprehensive Summaries of Uppsala Dissertations from the Faculty of Medicine 122 Genetic and Epigenetic Variation in the Human Genome Analysis of Phenotypically Normal Individuals and Patients Affected with Brain Tumors CECILIA DE BUSTOS ACTA UNIVERSITATIS UPSALIENSIS ISSN 1651-6206 UPPSALA ISBN 91-554-6490-4 2006 urn:nbn:se:uu:diva-6629 !" #$ % &' !""( ")*&+ , $ , , -$ $ ./ , 0 12 #$ 3 4 $2 5 62 !""(2 7 4 8 $ 7 2 % , -$ 9 : - %,, 3 $ 5 # 2 % 2 &!!2 (; 2 2 :<59 )&=++>=(>)"=>2 7 , $ $ 2 < $ .<9-1 $ .69-1 $ , , 2 #$ $ $ , = $ 2 6 , , $ 3 $ 2 : : 3 ,, $ , -7/? ,, 3 $ $ @ $ $ $ 2 % , = , $ .!A1 3 , , $ B9/&>;C-7/? $3 $ $ 2 : :: +" 3 @ , 9% 3 $ $ !! 2 D$ !"E , !! ,, , $ !! 3 , &>E , 2 #$ $ , !!F2 - ::: $ , , 'G $ 2 D +&2+E , $ 2 : 3 , 3 , !2! 0 '!" . $ 4 69-12 : 3$ $ 4 69- 3 $ $ $ 3 $ 3 $$= -6 = $ . :812 / $ 3 ! 3$$ $ , 2 #$ $ 3 , 3 $ , 2 H $ 3 @ !)" 2 #$, :=:8 $ <9- 69- = $2 / 8 , 9% $ , ,, I)E , $ $ 2 0 $ $ $ 3 , 3 9% $ , 2 "# $ =67 $ % & & -

Supplementary Table 1: Genes Affected by Anoikis. A, Ratio of Signal
Supplementary Table 1: Genes affected by anoikis. a, ratio of signal intensity of nonanchored cells anchorage dependent cells (CasKoSrc) over anchored cells; b, induced by Src transformation of Cx43KO cells; c, decreased by Src transformation of Cx43Ko cells; *, induced by normalization of Src transformed cells by neighboring nontransformed cells. Gene Symbol Probe Set Fold Changea Gene Name increased Selenbp1 1450699_at 23.22 selenium binding protein 1 Dscr1l1 1450243_a_at 10.77 Down syndrome critical region gene 1-like 1 Dscr1l1 1421425_a_at 4.29 Down syndrome critical region gene 1-like 1 Ttyh1 1426617_a_at 6.70 tweety homolog 1 (Drosophila) 5730521E12Rik 1419065_at 6.16 RIKEN cDNA 5730521E12 gene c 6330406I15Rik 1452244_at 5.87 RIKEN cDNA 6330406I15 gene AF067063 1425160_at 5.73 clone L2 uniform group of 2-cell-stage gene family mRNA Morc 1419418_a_at 5.55 microrchidia c Gpr56 1421118_a_at 5.43 G protein-coupled receptor 56 Pax6 1452526_a_at 5.06 paired box gene 6 Tgfbi 1415871_at 3.73 transforming growth factor beta induced Adarb1 1434932_at 3.70 adenosine deaminase RNA-specific B1 Ddx3y 1452077_at 3.30 DEAD (Asp-Glu-Ala-Asp) box polypeptide 3 Y-linked b Ampd3 1422573_at 3.20 AMP deaminase 3 Gli2 1459211_at 3.07 GLI-Kruppel family member GLI2 Selenbp2 1417580_s_at 2.96 selenium binding protein 2 Adamts1 1450716_at 2.80 a disintegrin-like and metalloprotease with thrombospondin type 1 motif 1 Dusp15 1426189_at 2.70 dual specificity phosphatase-like 15 Dpep3 1429035_at 2.60 dipeptidase 3 Sepp1 1452141_a_at 2.57 selenoprotein P plasma -

Rabbit Anti-FAM19A1/FITC Conjugated Antibody-SL14779R
SunLong Biotech Co.,LTD Tel: 0086-571- 56623320 Fax:0086-571- 56623318 E-mail:[email protected] www.sunlongbiotech.com Rabbit Anti-FAM19A1/FITC Conjugated antibody SL14779R-FITC Product Name: Anti-FAM19A1/FITC Chinese Name: FITC标记的FAM19A1蛋白抗体 C630007B19Rik,; Chemokine-like protein TAFA-1; F19A1_HUMAN; Fam19a1; Alias: Family with sequence similarity 19 (chemokine (C-C motif) like), member A1; Protein FAM19A1; RGD1563030; TAFA 1; TAFA1. Organism Species: Rabbit Clonality: Polyclonal React Species: Human,Mouse,Rat,Chicken,Dog,Pig,Cow, ICC=1:50-200IF=1:50-200 Applications: not yet tested in other applications. optimal dilutions/concentrations should be determined by the end user. Molecular weight: 13kDa Form: Lyophilized or Liquid Concentration: 1mg/ml immunogen: KLH conjugated synthetic peptide derived from human FAM19A1 Lsotype: IgG Purification: affinity purified by Protein A Storage Buffer: 0.01Mwww.sunlongbiotech.com TBS(pH7.4) with 1% BSA, 0.03% Proclin300 and 50% Glycerol. Store at -20 °C for one year. Avoid repeated freeze/thaw cycles. The lyophilized antibody is stable at room temperature for at least one month and for greater than a year Storage: when kept at -20°C. When reconstituted in sterile pH 7.4 0.01M PBS or diluent of antibody the antibody is stable for at least two weeks at 2-4 °C. background: A group of small secreted proteins known as the TAFA family consists of five highly homologous genes: TAFA1, TAFA2, TAFA3, TAFA4 and TAFA5. Members of the TAFA family contain conserved cysteine residues at fixed positions and are highly Product Detail: expressed in brain. The TAFA family may be distantly related to a member of the CC- chemokine family known as MIP-1A, and have been postulated to regulate nervous and immune cells of the brain as neurokines or chemokines. -

A B-Catenin-Driven Switch in TCF/LEF Transcription Factor Binding To
RESEARCH ARTICLE A b-catenin-driven switch in TCF/LEF transcription factor binding to DNA target sites promotes commitment of mammalian nephron progenitor cells Qiuyu Guo1, Albert Kim1, Bin Li2, Andrew Ransick1, Helena Bugacov1, Xi Chen1, Nils Lindstro¨ m1, Aaron Brown3, Leif Oxburgh2, Bing Ren4, Andrew P McMahon1* 1Department of Stem Cell Biology and Regenerative Medicine, Eli and Edythe Broad-CIRM Center for Regenerative Medicine and Stem Cell Research, Keck School of Medicine of the University of Southern California, Los Angeles, United States; 2The Rogosin Institute, New York, United States; 3Center for Molecular Medicine, Maine Medical Center Research Institute, Scarborough, United States; 4Ludwig Institute for Cancer Research, Department of Cellular and Molecular Medicine, Institute of Genomic Medicine, Moores Cancer Center, University of California San Diego, San Diego, United States Abstract The canonical Wnt pathway transcriptional co-activator b-catenin regulates self-renewal and differentiation of mammalian nephron progenitor cells (NPCs). We modulated b-catenin levels in NPC cultures using the GSK3 inhibitor CHIR99021 (CHIR) to examine opposing developmental actions of b-catenin. Low CHIR-mediated maintenance and expansion of NPCs are independent of direct engagement of TCF/LEF/b-catenin transcriptional complexes at low CHIR-dependent cell- cycle targets. In contrast, in high CHIR, TCF7/LEF1/b-catenin complexes replaced TCF7L1/TCF7L2 binding on enhancers of differentiation-promoting target genes. Chromosome confirmation studies -

TAFA5 Lentiviral Activation Particles (H): Sc-411807-LAC
SANTA CRUZ BIOTECHNOLOGY, INC. TAFA5 Lentiviral Activation Particles (h): sc-411807-LAC BACKGROUND APPLICATIONS The Clustered Regularly Interspaced Short Palindromic Repeats (CRISPR) and Either TAFA5 Lentiviral Activation Particles (h) or TAFA5 Lentiviral Activation CRISPR-associated protein (Cas9) system is an adaptive immune response Particles (h2) is recommended for gene activation in human cells. defense mechanism used by archea and bacteria for the degradation of for- eign genetic material. This mechanism can be repurposed for other functions, SUPPORT REAGENTS including genomic engineering for mammalian systems, such as gene knock- For optimal reaction efficiency with Lentiviral Activation Particle products, out (KO) (1,2) and gene activation (3-5). CRISPR Activation Plasmid products Polybrene®: sc-134220 (10 mg/ml) is recommended. Hygromycin B solution: enable the identification and upregulation of specific genes by utilizing a sc-29067 (1 g), Blasticidin S HCl solution: sc-495389 (1 ml) and Puromycin D10A and N863A deactivated Cas9 (dCas9) nuclease fused to a VP64 acti- dihydrochloride: sc-108071 (25 mg) are recommended for selection. Control vation domain, in conjunction with sgRNA (MS2), a target-specific sgRNA Lentiviral Activation Particles: sc-437282 (200 µl) negative control is also engineered to bind the MS2-P65-HSF1 fusion protein (5). This synergistic available. activation mediator (SAM) transcription activation system* provides a robust system to maximize the activation of endogenous gene expression (5). BIOSAFETY REFERENCES Lentiviral particles can be employed in standard Biosafety Level 2 tissue cul- ture facilities (and should be treated with the same level of caution as with 1. Cong, L., et al. 2013. Multiplex genome engineering using CRISPR/Cas any other potentially infectious reagent). -

WO 2019/003162 Al 03 January 2019 (03.01.2019) W !P O PCT
(12) INTERNATIONAL APPLICATION PUBLISHED UNDER THE PATENT COOPERATION TREATY (PCT) (19) World Intellectual Property Organization International Bureau (10) International Publication Number (43) International Publication Date WO 2019/003162 Al 03 January 2019 (03.01.2019) W !P O PCT (51) International Patent Classification: Published: A61K 39/395 (2006.01) A61P 29/00 (2006.01) — with international search report (Art. 21(3)) A61P 27/06 (2006.01) A61K 39/00 (2006.01) — before the expiration of the time limit for amending the (21) International Application Number: claims and to be republished in the event of receipt of PCT/IB20 18/054782 amendments (Rule 48.2(h)) — with sequence listing part of description (Rule 5.2(a)) (22) International Filing Date: — in black and white; the international application as filed 27 June 2018 (27.06.2018) contained color or greyscale and is availablefor download (25) Filing Language: English from PATENTSCOPE (26) Publication Language: English (30) Priority Data: 62/525,639 27 June 2017 (27.06.2017) US 62/582,889 07 November 2017 (07. 11.20 17) US (71) Applicant: NEURACLE SCIENCE CO., LTD. [KR/KR]; Anam-ro 145, 702-2ho, Seongbuk-Gu, Seoul 136-713 (KR). (72) Inventors: KIM, BongCheol; 155, Dongpangyo-ro, Bun- dang-gu, Seongnam-Si, Gyeonggi-do 13525 (KR). KIM, Dong Sik; Doosan-Apt 114-1301, Bongcheon-ro 387, Gwanak-Gu, Seoul (KR). KWON, Soon-gu; Gwanak Dreamtown APT 132-2703, Seonghyeon-ro 80, Gwanak- Gu, Seoul (KR). (81) Designated States (unless otherwise indicated, for every kind of national protection available): AE, AG, AL, AM, AO, AT, AU, AZ, BA, BB, BG, BH, BN, BR, BW, BY, BZ, CA, CH, CL, CN, CO, CR, CU, CZ, DE, DJ, DK, DM, DO, DZ, EC, EE, EG, ES, FI, GB, GD, GE, GH, GM, GT, HN, HR, HU, ID, IL, IN, IR, IS, JO, JP, KE, KG, KH, KN, KP, KR, KW, KZ, LA, LC, LK, LR, LS, LU, LY, MA, MD, ME, MG, MK, MN, MW, MX, MY, MZ, NA, NG, NI, NO, NZ, OM, PA, PE, PG, PH, PL, PT, QA, RO, RS, RU, RW, SA, SC, SD, SE, SG, SK, SL, SM, ST, SV, SY, TH, TJ, TM, TN, TR, TT, TZ, UA, UG, US, UZ, VC, VN, ZA, ZM, ZW. -
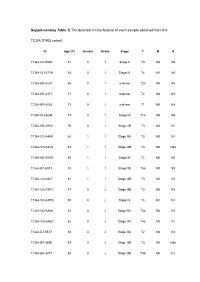
Supplementary Table 1| the Detailed Clinical Feature of Each Sample Obtained from The
Supplementary Table 1| The detailed clinical feature of each sample obtained from the TCGA STAD cohort. ID Age (Y) Gender Grade Stage T M N TCGA-CD-5800 51 0 1 Stage II T3 M0 N0 TCGA-CG-5719 54 0 1 Stage IV T4 M1 N0 TCGA-BR-4201 66 0 1 unknow T2a M0 NX TCGA-BR-4371 71 0 1 unknow T2 M0 NX TCGA-BR-4292 73 0 1 unknow T1 M0 NX TCGA-HU-8244 77 0 1 Stage IA T1a M0 N0 TCGA-KB-A93H 79 0 1 Stage IIB T3 M0 N1 TCGA-CD-A4MI 62 1 1 Stage IIIA T3 M0 N1 TCGA-VQ-A91A 67 1 1 Stage IIIB T3 M0 N3a TCGA-KB-A93G 68 1 1 Stage IB T2 M0 N0 TCGA-B7-A5TJ 74 1 1 Stage IIB T4a M0 NX TCGA-VQ-A927 81 1 1 Stage IIIB T3 M0 N3 TCGA-VQ-A8PY 47 0 2 Stage IIIB T3 M0 N2 TCGA-VQ-A8PQ 50 0 2 Stage IV T4 M1 N1 TCGA-VQ-AA68 52 0 2 Stage IIIC T4a M0 N3 TCGA-VQ-AA6D 52 0 2 Stage IIIA T4a M0 N1 TCGA-D7-5577 53 0 2 Stage IIIA T2 M0 N3 TCGA-BR-8690 54 0 2 Stage IIIB T3 M0 N3a TCGA-BR-8077 58 0 2 Stage IIIB T4b M0 N1 TCGA-HU-A4H2 58 0 2 Stage IIIB T3 M0 N3b TCGA-VQ-A91N 59 0 2 Stage IV T4 M0 N3 TCGA-D7-A74A 61 0 2 Stage IIIA T3 M0 N2 TCGA-HU-A4GP 62 0 2 Stage IIA T2 M0 N1 TCGA-BR-7716 62 0 2 Stage IIB T3 M0 N1 TCGA-BR-8679 63 0 2 Stage IB T2 M0 N0 TCGA-BR-8373 65 0 2 Stage IIIA T4a M0 N1 TCGA-VQ-A8PB 65 0 2 Stage II T3 M0 N0 TCGA-R5-A7ZF 65 0 2 Stage IV T4a M1 N1 TCGA-CG-4460 66 0 2 Stage IV T4 M1 N1 TCGA-D7-8579 66 0 2 Stage IIB T2 M0 N2 TCGA-R5-A7ZE 66 0 2 Stage IIIA T3 M0 N2 TCGA-VQ-A91Z 67 0 2 Stage IIIA T3 M0 N1 TCGA-HU-A4G9 67 0 2 Stage IA T1a M0 N0 TCGA-D7-6526 67 0 2 Stage IIIA T3 M0 N2 TCGA-BR-A4PE 68 0 2 Stage IB T2 M0 N0 TCGA-VQ-A8DL 69 0 2 Stage IIA T3 M0 N0 TCGA-BR-A4J6 -

Is FAM19A5 an Adipokine? Peripheral FAM19A5 in Wild-Type, FAM19A5 Knock-Out, and Lacz Knock-In Mice
bioRxiv preprint doi: https://doi.org/10.1101/2020.02.19.955351; this version posted February 20, 2020. The copyright holder for this preprint (which was not certified by peer review) is the author/funder, who has granted bioRxiv a license to display the preprint in perpetuity. It is made available under aCC-BY-ND 4.0 International license. Is FAM19A5 an adipokine? Peripheral FAM19A5 in wild-type, FAM19A5 knock-out, and LacZ knock-in mice Hoyun Kwak1§, Eun-Ho Cho1§, Eun Bee Cho1, Yoo-Na Lee2, Anu Shahapal2, Hyo Jeong Yong2, Arfaxad Reyes-Alcaraz3, Yongwoo Jeong1, Yerim Lee1, Minhyeok Lee1, Nui Ha1, Sitaek Oh1, Jae Keun Lee1, Won Suk Lee1, Wonkyum Kim1, Jong-Ik Hwang2, and Jae Young Seong2* 1Neuracle Science Co. Ltd., Seoul 02841, Republic of Korea 2Graduate School of Biomedical Sciences, Korea University College of Medicine, Seoul 02841, Republic of Korea 3College of Pharmacy, University of Houston, Texas, United States of America §H.K. and E-HC contributed equally to this work. *Correspondence: Jae Young Seong, Ph. D Graduate School of Biomedical Sciences, Korea University College of Medicine, Seoul 02841, Republic of Korea Tel: +82-2-2286-1090; Fax: +82-2-921-4355 [email protected] Short title: FAM19A5 in peripheral tissues Keywords: FAM19A5, peripheral expression, brain, adipose tissue, qRT-PCR, ELISA, Western blot Abstract FAM19A5 (also called TAFA5) is a novel secretory protein that is primarily expressed in the brain. However, a recent study reported that FAM19A5 is an adipocyte-derived adipokine that regulates vascular smooth muscle function. Furthermore, genome-wide association study (GWAS) and RNA-seq analyses revealed that the FAM19A5 was associated with a variety of diseases and tumorigenesis in peripheral tissues. -

Gene Networks Constructed Through Simulated Treatment Learning Can Predict Proteasome Inhibitor Benefit in Multiple Myeloma
Published OnlineFirst September 10, 2020; DOI: 10.1158/1078-0432.CCR-20-0742 CLINICAL CANCER RESEARCH | PRECISION MEDICINE AND IMAGING Gene Networks Constructed Through Simulated Treatment Learning can Predict Proteasome Inhibitor Benefit in Multiple Myeloma A C Joske Ubels1,2,3,4, Pieter Sonneveld3, Martin H. van Vliet4, and Jeroen de Ridder1,2 ABSTRACT ◥ Purpose: Proteasome inhibitors are widely used in treating we found an HR of 0.47 (P ¼ 0.04) in favor of bortezomib, while in multiple myeloma, but can cause serious side effects and response class “no benefit,” the HR was 0.91 (P ¼ 0.68). Importantly, we varies among patients. It is, therefore, important to gain more observed a similar performance (HR class benefit, 0.46; P ¼ 0.04) in insight into which patients will benefit from proteasome inhibitors. an independent patient cohort. Moreover, this signature also pre- Experimental Design: We introduce simulated treatment dicts benefit for the proteasome inhibitor, carfilzomib, indicating it learned signatures (STLsig), a machine learning method to identify is not specific to bortezomib. No equivalent signature can be found predictive gene expression signatures. STLsig uses genetically sim- when the genes in the signature are excluded from the analysis, ilar patients who have received an alternative treatment to model indicating that they are essential. Multiple genes in the signature are which patients will benefit more from proteasome inhibitors than linked to working mechanisms of proteasome inhibitors or multiple from an alternative treatment. STLsig constructs gene networks by myeloma disease progression. linking genes that are synergistic in their ability to predict benefit. Conclusions: STLsig can identify gene signatures that could aid Results: In a dataset of 910 patients with multiple myeloma, in treatment decisions for patients with multiple myeloma and STLsig identified two gene networks that together can predict provide insight into the biological mechanism behind treatment benefit to the proteasome inhibitor, bortezomib. -

TAFA5 CRISPR/Cas9 KO Plasmid (M): Sc-430632
SANTA CRUZ BIOTECHNOLOGY, INC. TAFA5 CRISPR/Cas9 KO Plasmid (m): sc-430632 BACKGROUND APPLICATIONS The Clustered Regularly Interspaced Short Palindromic Repeats (CRISPR) and TAFA5 CRISPR/Cas9 KO Plasmid (m) is recommended for the disruption of CRISPR-associated protein (Cas9) system is an adaptive immune response gene expression in mouse cells. defense mechanism used by archea and bacteria for the degradation of foreign genetic material (4,6). This mechanism can be repurposed for other 20 nt non-coding RNA sequence: guides Cas9 functions, including genomic engineering for mammalian systems, such as to a specific target location in the genomic DNA gene knockout (KO) (1,2,3,5). CRISPR/Cas9 KO Plasmid products enable the U6 promoter: drives gRNA scaffold: helps Cas9 identification and cleavage of specific genes by utilizing guide RNA (gRNA) expression of gRNA bind to target DNA sequences derived from the Genome-scale CRISPR Knock-Out (GeCKO) v2 library developed in the Zhang Laboratory at the Broad Institute (3,5). Termination signal Green Fluorescent Protein: to visually REFERENCES verify transfection CRISPR/Cas9 Knockout Plasmid CBh (chicken β-Actin 1. Cong, L., et al. 2013. Multiplex genome engineering using CRISPR/Cas hybrid) promoter: drives systems. Science 339: 819-823. 2A peptide: expression of Cas9 allows production of both Cas9 and GFP from the 2. Mali, P., et al. 2013. RNA-guided human genome engineering via Cas9. same CBh promoter Science 339: 823-826. Nuclear localization signal 3. Ran, F.A., et al. 2013. Genome engineering using the CRISPR-Cas9 system. Nuclear localization signal SpCas9 ribonuclease Nat. Protoc. 8: 2281-2308. -
Gene Networks Constructed Through Simulated Treatment Learning Can
Author Manuscript Published OnlineFirst on September 10, 2020; DOI: 10.1158/1078-0432.CCR-20-0742 Author manuscripts have been peer reviewed and accepted for publication but have not yet been edited. Gene networks constructed through simulated treatment learning can predict proteasome inhibitor benefit in Multiple Myeloma Joske Ubels1,2,3,4, Pieter Sonneveld3, Martin H. van Vliet4 and Jeroen de Ridder1,2* 1. Center for Molecular Medicine, University Medical Center Utrecht, Universiteitsweg 100, 3584 CG, Utrecht, The Netherlands 2. Oncode Institute, Utrecht, The Netherlands 3. Department of Hematology, Erasmus MC Cancer Institute, Wytemaweg 80, 3015 CN, Rotterdam, The Netherlands 4. SkylineDx, Lichtenauerlaan 40, 3062 ME, Rotterdam, The Netherlands *corresponding author Running title: Gene networks can predict proteasome inhibitor benefit Corresponding author: Jeroen de Ridder Universiteitsweg 100, STR 1.305 3584 CG Utrecht, The Netherlands +31 (0)88 7550406 Conflict of interests J.U. and M.H.v.V are employed by SkylineDx. J.d.R. is co-founder of Cyclomics B.V. P.S served on an advisory board to SkylineDx. Translational relevance Proteasome inhibitors play an important part in the treatment of Multiple Myeloma, but response varies widely between patients. As proteasome inhibitors are associated with serious side effects and alternative treatments are available, there is a clinical need for a tool that can aid in treatment decision at the moment of diagnosis. We here present a gene expression signature that can identify patients that will benefit more from a proteasome inhibitor than an alternative treatment. We validate the signature in an independent dataset representing current clinical practice in Multiple Myeloma. -
Mouse Fam19a5 Knockout Project (CRISPR/Cas9)
https://www.alphaknockout.com Mouse Fam19a5 Knockout Project (CRISPR/Cas9) Objective: To create a Fam19a5 knockout Mouse model (C57BL/6N) by CRISPR/Cas-mediated genome engineering. Strategy summary: The Fam19a5 gene (NCBI Reference Sequence: NM_001252310 ; Ensembl: ENSMUSG00000054863 ) is located on Mouse chromosome 15. 4 exons are identified, with the ATG start codon in exon 1 and the TGA stop codon in exon 4 (Transcript: ENSMUST00000230414). Exon 2 will be selected as target site. Cas9 and gRNA will be co-injected into fertilized eggs for KO Mouse production. The pups will be genotyped by PCR followed by sequencing analysis. Note: Exon 2 starts from about 28.54% of the coding region. Exon 2 covers 37.88% of the coding region. The size of effective KO region: ~150 bp. The KO region does not have any other known gene. Page 1 of 8 https://www.alphaknockout.com Overview of the Targeting Strategy Wildtype allele gRNA region 5' gRNA region 3' 1 2 4 Legends Exon of mouse Fam19a5 Knockout region Page 2 of 8 https://www.alphaknockout.com Overview of the Dot Plot (up) Window size: 15 bp Forward Reverse Complement Sequence 12 Note: The 150 bp section of Exon 2 is aligned with itself to determine if there are tandem repeats. No significant tandem repeat is found in the dot plot matrix. So this region is suitable for PCR screening or sequencing analysis. Overview of the Dot Plot (down) Window size: 15 bp Forward Reverse Complement Sequence 12 Note: The 150 bp section of Exon 2 is aligned with itself to determine if there are tandem repeats.