DOCSLIB.ORG

Investigating the Beehive Cluster with Gaia Blaise Whitesell — Astronomy Capstone 2019

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Investigating the Beehive Cluster with Gaia Blaise Whitesell — Astronomy Capstone 2019 Investigating the Beehive Cluster with Gaia Blaise Whitesell — Astronomy Capstone 2019 In this problem set, we will explore the capabilities of the publicly available data from Gaia DR2, which can be found at http://gea.esac.esa.int/archive/ or queried directly from within Python. We will focus on a single target: the Beehive cluster (M44, also known as Praesepe or NGC 2632). This open cluster is located at a distance of roughly 200 pc in the constellation Cancer with coordinates (α; δ) = (130:1°; 19:67°). We will download Gaia data in the vicinity of the cluster, select only the stars belonging to the cluster, and then characterize the properties of those stars in the cluster. 1. Getting Data For our analysis we need these columns from the Gaia DR2 database gaiadr2.gaia_source: source_id A numeric identifier for the object ra Right ascension (degrees) dec Declination (degrees) parallax Parallax (mas) pmra Proper motion in right ascension (mas/yr) pmdec Proper motion in declination (mas/yr) phot_g_mean_mag Magnitude in Gaia G band (mags) bp_rp Gaia BP–RP color (mags) Select objects within 4 degrees of the cluster center. At the rough distance of the Beehive cluster, how many parsecs does that correspond to? We want to include objects at least that far in front and behind the cluster. Since we don’t know distances as precisely, we should expand the range by a factor of 3 or 4 to avoid missing cluster stars. What parallaxes (in mas) does this distance range correspond to? Use those parallax values as conditions to exclude objects far away from the cluster. Also add some conditions to select only good quality data. Let’s say less than 5% parallax error, and less than 0.05 mags uncertainty in the faintest band BP. (Within these constraints, the uncertainties in position and proper motion will also be low.) At the cluster distance, what does a 5% parallax uncertainty correspond to? Here is a sample SQL query including these conditions that can be executed in Python: 1 import os 2 from astropy.table import Table 3 from astroquery.gaia import Gaia 4 5 query= """ 6 SELECT source_id,ra,dec,parallax,pmra,pmdec,phot_g_mean_mag,bp_rp 7 FROM gaiadr2.gaia_source 8 WHERE 1 = CONTAINS(POINT('ICRS', ra, dec), 1 2 9 CIRCLE('ICRS', 130.1, 19.67, 4.0)) 10 AND parallax > 4 11 AND parallax < 7 12 AND parallax_over_error > 20 13 AND phot_bp_mean_flux_over_error > 20; 14 """ 15 filename= 'beehive.dat' 16 if not os.path.isfile(filename): 17 Gaia.launch_job_async(query, output_file=filename, 18 dump_to_file=True, verbose=True) 19 results= Table.read(filename) Hints: Depending on server demand, the query may take several minutes to complete. This implementation only launches the query if the filename doesn’t exist, so you can rerun the code and use data already downloaded. The columns of the table can be accessed like so: results['source_id']. • How many objects did your query return? 2. Determining Cluster Membership Plot a sky projection of the points in your data sample, with right ascension on the x-axis and declination on the y-axis. Hints: The distribution should be circular. If yours is not, make sure you have an equal aspect ratio on your plot (e.g. .set_aspect('equal')). Reduce the size of the points (e.g. s=1) so it is possible to see where they are denser. Finally, reverse the x-axis (e.g. .invert_xaxis()) to match how the cluster appears on the sky. • Are there more stars at the center? p Now we want to slice our data by angular distance from the center. Calculate r = x2 + y2, where x and y are the offsets from the center in α and δ. Hints: Remember the cos(δ) term! Also remember that NumPy trig functions take arguments in radians (e.g. np.cos(np.radians(dec)) if you have dec in degrees). Try three slices: (r < 1°), (1° < r < 3°), and (3° < r < 4°). For each of these slices, make a histogram of the distances to the stars in the slice. You will need to calculate distance from parallax. Hints: Use an appropriate number of bins; ten is certainly too few. Also ensure that all three histograms use the same bins. If you plot the histograms separately, make sure the axis limits are the same on each. If you plot the histograms on the same axis, be careful that one doesn’t get lost behind another. • Does the histogram of the central field look different from that of the outer field? • How does the middle region compare? • Based on the distribution of stars in the center region, calculate an estimate of the distance to the cluster. 3 Make a scatter plot of the α and δ components of proper motion, displaying your slices in different colors. Hints: You will probably need to zoom in to see structure. Choose appropriate axis limits. It may be helpful to make a second plot on a smaller scale. • Do the stars at the center have a distribution different from that of the field? Explain why. Choose reasonable upper and lower bounds for each component to select stars most likely to be part of the cluster. To determine the spatial extent of the cluster, we will make a projected density profile. (The parallax uncertainties are not low enough to compare line-of-sight distances from the center with projected distances from the center on the scale of the cluster.) Convert your angular distance from the cluster center to a physical distance in parsecs, and bin the data into 0:5 pc bins. Plot the resulting density profile, with projected radius on the x-axis and number of stars per square parsec on the y-axis. Hints: To find the number density, calculate the number of stars in each bin as well as the volume of each bin. Remember to slice the data to only include objects with proper motions within the bounds you determined. Are linear or logarithmic axes appropriate for this plot? Based on your plot, estimate a reasonable cutoff value in projected distance corresponding to the radius of the cluster. Slice your dataset to include only objects within this projected radius. We can’t directly slice to include only objects with parallaxes placing them within this distance from the center, because the parallax errors are higher. A typical parallax error is about 3 pc. To avoid excluding too many cluster stars due to parallax error, use a line-of-sight distance cutoff 3 pc greater than your projected distance cutoff. Slice your dataset to include only objects within that parallax range. Now you have conditions for cluster membership in projected distance, line-of-sight distance, and proper motion. • How many stars do you find to be part of the cluster? Go back and make another plot of the sky projection, this time highlighting the cluster stars. Compare the density of cluster objects to background objects in the center of the sample and on the edges of the sample. Do your results make sense? Does the background density appear uniform? Also make another distance histogram. Do the objects you found to be part of the cluster follow a Gaussian distribution along the line of sight? Hint: If your distribution has fat tails, you might be including too many background objects. Conversely, if the distribution looks like the tails have been chopped off, you might be excluding too many cluster objects. Adjust your radius cutoff value accordingly. • Describe the radius cutoff you used and how you chose it. 4 3. Cluster Properties Once you are satisfied with your chosen conditions, use the resulting sample of cluster stars to determine properties of the cluster. • What is the center of your cluster sample? How does it compare to the given value of (α; δ) = (130:1°; 19:67°)? • Refine your estimate of the cluster distance. Is it similar to your first estimate? Do you think repeating the analysis with the new value would affect your results? • Calculate the mean proper motion (in mas=yr) and transverse spatial velocity of the cluster (in km=s), in (α; δ) components. Now construct a color-magnitude diagram of the cluster, calculating the absolute magnitude of each star from its parallax. You will also need to correct G magnitude for extinction and BP–RP color for reddening. In the vicinity of the Beehive cluster, E(B–V) = 0.027 mags. The extinction coefficients for the Gaia bandpasses are AG = 2:74 E(B–V), ABP = 3:374 E(B–V), and ARP = 2:035 E(B–V). These offsets will not change the shape of the CMD, but will allow accurate comparison to theoretical stellar populations so we can determine properties of the cluster. Also plot where the Sun would fall with MG; = 4:67, (BP–RP) = 0:82. • Describe what types of stars you see in the different parts of the color-magnitude diagram. • Compare to a published color-magnitude diagram such as Figure 2 on page 4 of Yang, Chen, & Zhao 2015. https://ui.adsabs.harvard.edu/abs/2015AJ....150..158Y/abstract Isochrones are provided for a range of possible ages and metallicities of the cluster. The necessary columns in the datafiles are G, G_BP, and G_RP, which are the magnitudes in each band. Overplot isochrones for young, 100 Myr populations of metallicities Z = 0:005, Z = 0:01, and Z = 0:02. • What is the approximate metallicity of the cluster? Overplot isochrones of your chosen metallicity for populations of ages 300 Myr, 1 Gyr, 3 Gyr, and 10 Gyr. • Approximately how old do you think the cluster is? Plot the cumulative luminosity profile L(R) for the cluster.
Load more

Recommended publications
  • Messier Objects
    Messier Objects From the Stocker Astroscience Center at Florida International University Miami Florida The Messier Project Main contributors: • Daniel Puentes • Steven Revesz • Bobby Martinez Charles Messier • Gabriel Salazar • Riya Gandhi • Dr. James Webb – Director, Stocker Astroscience center • All images reduced and combined using MIRA image processing software. (Mirametrics) What are Messier Objects? • Messier objects are a list of astronomical sources compiled by Charles Messier, an 18th and early 19th century astronomer. He created a list of distracting objects to avoid while comet hunting. This list now contains over 110 objects, many of which are the most famous astronomical bodies known. The list contains planetary nebula, star clusters, and other galaxies. - Bobby Martinez The Telescope The telescope used to take these images is an Astronomical Consultants and Equipment (ACE) 24- inch (0.61-meter) Ritchey-Chretien reflecting telescope. It has a focal ratio of F6.2 and is supported on a structure independent of the building that houses it. It is equipped with a Finger Lakes 1kx1k CCD camera cooled to -30o C at the Cassegrain focus. It is equipped with dual filter wheels, the first containing UBVRI scientific filters and the second RGBL color filters. Messier 1 Found 6,500 light years away in the constellation of Taurus, the Crab Nebula (known as M1) is a supernova remnant. The original supernova that formed the crab nebula was observed by Chinese, Japanese and Arab astronomers in 1054 AD as an incredibly bright “Guest star” which was visible for over twenty-two months. The supernova that produced the Crab Nebula is thought to have been an evolved star roughly ten times more massive than the Sun.
    [Show full text]
  • 2020 Observatory Schedule
    Astronomy Club of Akron 2020 Observatory Schedule 5031 Manchester Road, Akron, OH www.acaoh.org – The following events are open to the public. Please join us for stargazing and educational activities. Please arrive on time to avoid headlight distraction. – For notice of “impromptu star parties” not listed, send e-mail to [email protected] to request e-mail notification of unscheduled observing sessions. – Events will be cancelled if skies are cloudy. Always check website for star party status two hours before event. – This is an outdoor activity in an unheated environment. Nighttime temperatures drop rapidly, even during summer. A general rule of thumb is to dress for 15 degrees cooler than predicted nighttime low temperature. – Please respect those who set up their telescopes. Children should be supervised at all times. The observatory grounds are no place for toys or tomfoolery. – Please, No Smoking on observatory grounds. Smoke reacts with optical surfaces, damaging optical coatings. – Please, no use of cell phones or tablets in observatory (to preserve night vision). April 18 – 8:15pm July 18 – 9:00pm Venus is well placed for observing early, and then we’ll view Come out to view open cluster NGC6633, Wild Duck Ghost of Jupiter and the beautiful star cluster M37 through Cluster, Ring Nebula, M26 Star Cloud, and Swan Nebula the 16” observatory telescope and view Beehive Cluster using an OIII filter. through the 100mm wide field telescope. July 25 – 9:00pm April 25 – 8:30pm We’ll be observing a 5-day old Moon. This is a great Special Event: Messier Marathon – stay all night to observe opportunity to see crater central peaks lit up by the grazing all 110 Messier objects with ACA members.
    [Show full text]
  • PUBLIC OBSERVING NIGHTS the William D. Mcdowell Observatory
    THE WilliamPUBLIC D. OBSERVING mcDowell NIGHTS Observatory FREE PUBLIC OBSERVING NIGHTS WINTER Schedule 2019 December 2018 (7PM-10PM) 5th Mars, Uranus, Neptune, Almach (double star), Pleiades (M45), Andromeda Galaxy (M31), Oribion Nebula (M42), Beehive Cluster (M44), Double Cluster (NGC 869 & 884) 12th Mars, Uranus, Neptune, Almach (double star), Pleiades (M45), Andromeda Galaxy (M31), Oribion Nebula (M42), Beehive Cluster (M44), Double Cluster (NGC 869 & 884) 19th Moon, Mars, Uranus, Neptune, Almach (double star), Pleiades (M45), Andromeda Galaxy (M31), Oribion Nebula (M42), Beehive Cluster (M44), Double Cluster (NGC 869 & 884) 26th Moon, Mars, Uranus, Neptune, Almach (double star), Pleiades (M45), Andromeda Galaxy (M31), Oribion Nebula (M42), Beehive Cluster (M44), Double Cluster (NGC 869 & 884)? January 2019 (7PM-10PM) 2nd Moon, Mars, Uranus, Neptune, Sirius, Almach (double star), Pleiades (M45), Orion Nebula (M42), Open Cluster (M35) 9th Mars, Uranus, Neptune, Sirius, Almach (double star), Pleiades (M45), Orion Nebula (M42), Open Cluster (M35) 16 Mars, Uranus, Neptune, Sirius, Almach (double star), Pleiades (M45), Orion Nebula (M42), Open Cluster (M35) 23rd, Moon, Mars, Uranus, Neptune, Sirius, Almach (double star), Pleiades (M45), Andromeda Galaxy (M31), Orion Nebula (M42), Beehive Cluster (M44), Double Cluster (NGC 869 & 884) 30th Moon, Mars, Uranus, Neptune, Sirius, Almach (double star), Pleiades (M45), Andromeda Galaxy (M31), Orion Nebula (M42), Beehive Cluster (M44), Double Cluster (NGC 869 & 884) February 2019 (7PM-10PM) 6th
    [Show full text]
  • March 2021 These Pages Are Intended to Help You Find Your Way Around the Sky
    WHAT'S UP THIS MONTH – MARCH 2021 THESE PAGES ARE INTENDED TO HELP YOU FIND YOUR WAY AROUND THE SKY The chart above shows the whole night sky as it appears on 15th March at 21:00 (9 o’clock) Greenwich Mean Time (GMT). As the Earth orbits the Sun and we look out into space each night the stars will appear to have moved across the sky by a small amount. Every month Earth moves one twelfth of its circuit around the Sun, this amounts to 30 degrees each month. There are about 30 days in each month so each night the stars appear to move about 1 degree. The sky will therefore appear the same as shown on the chart above at 8 o’clock GMT at the beginning of the month and at 10 o’clock GMT at the end of the month. The stars also appear to move 15º (360º divided by 24) each hour from east to west, due to the Earth rotating once every 24 hours. The centre of the chart will be the position in the sky directly overhead, called the Zenith. First we need to find some familiar objects so we can get our bearings. The Pole Star Polaris can be easily found by first finding the familiar shape of the Great Bear ‘Ursa Major’ that is also sometimes called the Plough or even the Big Dipper by the Americans. Ursa Major is visible throughout the year from Britain and is always quite easy to find. This month it is high in the North East.
    [Show full text]
  • MESSIER 15 RA(2000) : 21H 29M 58S DEC(2000): +12° 10'
    MESSIER 15 RA(2000) : 21h 29m 58s DEC(2000): +12° 10’ 01” BASIC INFORMATION OBJECT TYPE: Globular Cluster CONSTELLATION: Pegasus BEST VIEW: Late October DISCOVERY: Jean-Dominique Maraldi, 1746 DISTANCE: 33,600 ly DIAMETER: 175 ly APPARENT MAGNITUDE: +6.2 APPARENT DIMENSIONS: 18’ FOV:Starry 1.00Night FOV: 60.00 Vulpecula Sagitta Pegasus NGC 7009 (THE SATURN NEBULA) Delphinus NGC 7009 RA(2000) : 21h 04m 10.8s DEC(2000): -11° 21’ 48.6” Equuleus Pisces Aquila NGC 7009 FOV: 5.00 Aquarius Telrad Capricornus Sagittarius Cetus Piscis Austrinus NGC 7009 Microscopium BASIC INFORMATION OBJECT TYPE: Planetary Nebula CONSTELLATION: Aquarius Sculptor BEST VIEW: Early November DISCOVERY: William Herschel, 1782 DISTANCE: 2000 - 4000 ly DIAMETER: 0.4 - 0.8 ly Grus APPARENT MAGNITUDE: +8.0 APPARENT DIMENSIONS: 41” x 35” Telescopium Telrad Indus NGC 7662 (THE BLUE SNOWBALL) RA(2000) : 23h 25m 53.6s DEC(2000): +42° 32’ 06” BASIC INFORMATION OBJECT TYPE: Planetary Nebula CONSTELLATION: Andromeda BEST VIEW: Late November DISCOVERY: William Herschel, 1784 DISTANCE: 1800 – 6400 ly DIAMETER: 0.3 – 1.1 ly APPARENT MAGNITUDE: +8.6 APPARENT DIMENSIONS: 37” MESSIER 52 RA(2000) : 23h 24m 48s DEC(2000): +61° 35’ 36” BASIC INFORMATION OBJECT TYPE: Open Cluster CONSTELLATION: Cassiopeia BEST VIEW: December DISCOVERY: Charles Messier, 1774 DISTANCE: ~5000 ly DIAMETER: 19 ly APPARENT MAGNITUDE: +7.3 APPARENT DIMENSIONS: 13’ AGE: 50 million years FOV:Starry 1.00Night FOV: 60.00 Auriga Cepheus Andromeda MESSIER 31 (THE ANDROMEDA GALAXY) M 31 RA(2000) : 00h 42m 44.3Cassiopeias DEC(2000): +41° 16’ 07.5” Perseus Lacerta AndromedaM 31 FOV: 5.00 Telrad Triangulum Taurus Orion Aries Andromeda M 31 Pegasus Pisces BASIC INFORMATION OBJECT TYPE: Galaxy CONSTELLATION: Andromeda Telrad BEST VIEW: December DISCOVERY: Abd al-Rahman al-Sufi, 964 Eridanus CetusDISTANCE: 2.5 million ly DIAMETER: ~250,000 ly* APPARENT MAGNITUDE: +3.4 APPARENT DIMENSIONS: 178’ x 63’ (3° x 1°) *This value represents the total diameter of the disk, based on multi-wavelength measurements.
    [Show full text]
  • The Messier Catalog
    The Messier Catalog Messier 1 Messier 2 Messier 3 Messier 4 Messier 5 Crab Nebula globular cluster globular cluster globular cluster globular cluster Messier 6 Messier 7 Messier 8 Messier 9 Messier 10 open cluster open cluster Lagoon Nebula globular cluster globular cluster Butterfly Cluster Ptolemy's Cluster Messier 11 Messier 12 Messier 13 Messier 14 Messier 15 Wild Duck Cluster globular cluster Hercules glob luster globular cluster globular cluster Messier 16 Messier 17 Messier 18 Messier 19 Messier 20 Eagle Nebula The Omega, Swan, open cluster globular cluster Trifid Nebula or Horseshoe Nebula Messier 21 Messier 22 Messier 23 Messier 24 Messier 25 open cluster globular cluster open cluster Milky Way Patch open cluster Messier 26 Messier 27 Messier 28 Messier 29 Messier 30 open cluster Dumbbell Nebula globular cluster open cluster globular cluster Messier 31 Messier 32 Messier 33 Messier 34 Messier 35 Andromeda dwarf Andromeda Galaxy Triangulum Galaxy open cluster open cluster elliptical galaxy Messier 36 Messier 37 Messier 38 Messier 39 Messier 40 open cluster open cluster open cluster open cluster double star Winecke 4 Messier 41 Messier 42/43 Messier 44 Messier 45 Messier 46 open cluster Orion Nebula Praesepe Pleiades open cluster Beehive Cluster Suburu Messier 47 Messier 48 Messier 49 Messier 50 Messier 51 open cluster open cluster elliptical galaxy open cluster Whirlpool Galaxy Messier 52 Messier 53 Messier 54 Messier 55 Messier 56 open cluster globular cluster globular cluster globular cluster globular cluster Messier 57 Messier
    [Show full text]
  • Atlas Menor Was Objects to Slowly Change Over Time
    C h a r t Atlas Charts s O b by j Objects e c t Constellation s Objects by Number 64 Objects by Type 71 Objects by Name 76 Messier Objects 78 Caldwell Objects 81 Orion & Stars by Name 84 Lepus, circa , Brightest Stars 86 1720 , Closest Stars 87 Mythology 88 Bimonthly Sky Charts 92 Meteor Showers 105 Sun, Moon and Planets 106 Observing Considerations 113 Expanded Glossary 115 Th e 88 Constellations, plus 126 Chart Reference BACK PAGE Introduction he night sky was charted by western civilization a few thou - N 1,370 deep sky objects and 360 double stars (two stars—one sands years ago to bring order to the random splatter of stars, often orbits the other) plotted with observing information for T and in the hopes, as a piece of the puzzle, to help “understand” every object. the forces of nature. The stars and their constellations were imbued with N Inclusion of many “famous” celestial objects, even though the beliefs of those times, which have become mythology. they are beyond the reach of a 6 to 8-inch diameter telescope. The oldest known celestial atlas is in the book, Almagest , by N Expanded glossary to define and/or explain terms and Claudius Ptolemy, a Greco-Egyptian with Roman citizenship who lived concepts. in Alexandria from 90 to 160 AD. The Almagest is the earliest surviving astronomical treatise—a 600-page tome. The star charts are in tabular N Black stars on a white background, a preferred format for star form, by constellation, and the locations of the stars are described by charts.
    [Show full text]
  • 00E the Construction of the Universe Symphony
    The basic construction of the Universe Symphony. There are 30 asterisms (Suites) in the Universe Symphony. I divided the asterisms into 15 groups. The asterisms in the same group, lay close to each other. Asterisms!! in Constellation!Stars!Objects nearby 01 The W!!!Cassiopeia!!Segin !!!!!!!Ruchbah !!!!!!!Marj !!!!!!!Schedar !!!!!!!Caph !!!!!!!!!Sailboat Cluster !!!!!!!!!Gamma Cassiopeia Nebula !!!!!!!!!NGC 129 !!!!!!!!!M 103 !!!!!!!!!NGC 637 !!!!!!!!!NGC 654 !!!!!!!!!NGC 659 !!!!!!!!!PacMan Nebula !!!!!!!!!Owl Cluster !!!!!!!!!NGC 663 Asterisms!! in Constellation!Stars!!Objects nearby 02 Northern Fly!!Aries!!!41 Arietis !!!!!!!39 Arietis!!! !!!!!!!35 Arietis !!!!!!!!!!NGC 1056 02 Whale’s Head!!Cetus!! ! Menkar !!!!!!!Lambda Ceti! !!!!!!!Mu Ceti !!!!!!!Xi2 Ceti !!!!!!!Kaffalijidhma !!!!!!!!!!IC 302 !!!!!!!!!!NGC 990 !!!!!!!!!!NGC 1024 !!!!!!!!!!NGC 1026 !!!!!!!!!!NGC 1070 !!!!!!!!!!NGC 1085 !!!!!!!!!!NGC 1107 !!!!!!!!!!NGC 1137 !!!!!!!!!!NGC 1143 !!!!!!!!!!NGC 1144 !!!!!!!!!!NGC 1153 Asterisms!! in Constellation Stars!!Objects nearby 03 Hyades!!!Taurus! Aldebaran !!!!!! Theta 2 Tauri !!!!!! Gamma Tauri !!!!!! Delta 1 Tauri !!!!!! Epsilon Tauri !!!!!!!!!Struve’s Lost Nebula !!!!!!!!!Hind’s Variable Nebula !!!!!!!!!IC 374 03 Kids!!!Auriga! Almaaz !!!!!! Hoedus II !!!!!! Hoedus I !!!!!!!!!The Kite Cluster !!!!!!!!!IC 397 03 Pleiades!! ! Taurus! Pleione (Seven Sisters)!! ! ! Atlas !!!!!! Alcyone !!!!!! Merope !!!!!! Electra !!!!!! Celaeno !!!!!! Taygeta !!!!!! Asterope !!!!!! Maia !!!!!!!!!Maia Nebula !!!!!!!!!Merope Nebula !!!!!!!!!Merope
    [Show full text]
  • The Evening Sky Map
    I N E D R I A C A S T N E O D I T A C L E O R N I G D S T S H A E P H M O O R C I . Z N O p l f e i n h d o P t O o N ) l h a r g Z i u s , o I l C t P h R I r e o R N ( O o r C r H e t L p h p E E i s t D H a ( r g T F i . O B NORTH D R e N M h t E A X O e s A H U M C T . I P N S L E E P Z “ E A N H O NORTHERN HEMISPHERE M T R T Y N H E ” K E η ) W S . T T E W U B R N W D E T T W T H h A The Evening Sky Map e MAY 2021 E . C ) Cluster O N FREE* EACH MONTH FOR YOU TO EXPLORE, LEARN & ENJOY THE NIGHT SKY r S L a o K e Double r Y E t B h R M t e PERSEUS A a A r CASSIOPEIA n e S SKY MAP SHOWS HOW Get Sky Calendar on Twitter P δ r T C G C A CEPHEUS r E o R e J s O h Sky Calendar – May 2021 http://twitter.com/skymaps M39 s B THE NIGHT SKY LOOKS T U ( O i N s r L D o a j A NE I I a μ p T EARLY MAY PM T 10 r 61 M S o S 3 Last Quarter Moon at 19:51 UT.
    [Show full text]
  • The Messier Marathon Search Sequence
    2/28/2020 Messier Marathon Search Sequence List This file presents the Messier objects in the order of the Marathon Search Sequence given by Don Machholz in his Messier Marathon Observer's Guide. The Messier Marathon Search Sequence compiled online by Hartmut Frommert, using work of Don Machholz. Depending on geographic location, it may be impossible to find them all, and may be better to slightly modify this list. In case of doubt consult Don Machholz's book. This list should be good for northern latitudes 20 to 40. 1. M77 spiral galaxy in Cetus 2. M74 spiral galaxy in Pisces 3. M33 The Triangulum Galaxy (also Pinwheel) spiral galaxy in Triangulum 4. M31 The Andromeda Galaxy spiral galaxy in Andromeda 5. M32 Satellite galaxy of M31 elliptical galaxy in Andromeda 6. M110 Satellite galaxy of M31 elliptical galaxy in Andromeda 7. M52 open cluster in Cassiopeia 8. M103 open cluster in Cassiopeia 9. M76 The Little Dumbell, Cork, or Butterfly planetary nebula in Perseus 10. M34 open cluster in Perseus 11. M45 Subaru, the Pleiades--the Seven Sisters open cluster in Taurus 12. M79 globular cluster in Lepus 13. M42 The Great Orion Nebula diffuse nebula in Orion 14. M43 part of the Orion Nebula (de Mairan's Nebula) diffuse nebula in Orion 15. M78 diffuse reflection nebula in Orion 16. M1 The Crab Nebula supernova remnant in Taurus 17. M35 open cluster in Gemini 18. M37 open cluster in Auriga 19. M36 open cluster in Auriga 20. M38 open cluster in Auriga 21. M41 open cluster in Canis Major 22.
    [Show full text]
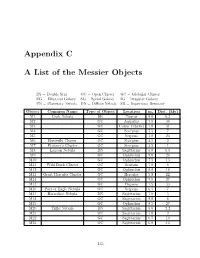
  • Appendix C a List of the Messier Objects
    Appendix C A List of the Messier Objects DS=DoubleStar OC=OpenCluster GC=GlobularCluster EG = Elliptical Galaxy SG = Spiral Galaxy IG = Irregular Galaxy PN = Planetary Nebula DN = Diffuse Nebula SR = Supernova Remnant Object Common Name Type of Object Location mv Dist. (kly) M1 Crab Nebula SR Taurus 9.0 6.3 M2 GC Aquarius 7.5 36 M3 GC Canes Venatici 7.0 31 M4 GC Scorpius 7.5 7 M5 GC Serpens 7.0 23 M6 Butterfly Cluster OC Scorpius 4.5 2 M7 Ptolemy’s Cluster OC Scorpius 3.5 1 M8 Lagoon Nebula DN Sagittarius 5.0 6.5 M9 GC Ophiuchus 9.0 26 M10 GC Ophiuchus 7.5 13 M11 Wild Duck Cluster OC Scutum 7.0 6 M12 GC Ophiuchus 8.0 18 M13 Great Hercules Cluster GC Hercules 5.8 22 M14 GC Ophiuchus 9.5 27 M15 GC Pegasus 7.5 33 M16 Part of Eagle Nebula OC Serpens 6.5 7 M17 Horseshoe Nebula DN Sagittarius 7.0 5 M18 OC Sagittarius 8.0 6 M19 GC Ophiuchus 8.5 27 M20 Trifid Nebula DN Sagittarius 5.0 2.2 M21 OC Sagittarius 7.0 3 M22 GC Sagittarius 6.5 10 M23 OC Sagittarius 6.0 4.5 135 Object Common Name Type of Object Location mv Dist. (kly) M24 Milky Way Patch Star cloud Sagittarius 11.5 10 M25 OC Sagittarius 4.9 2 M26 OC Scutum 9.5 5 M27 Dumbbell Nebula PN Vulpecula 7.5 1.25 M28 GC Sagittarius 8.5 18 M29 OC Cygnus 9.0 7.2 M30 GC Capricornus 8.5 25 M31 Andromeda Galaxy SG Andromeda 3.5 2500 M32 Satellite galaxy of M31 EG Andromeda 10.0 2900 M33 Triangulum Galaxy SG Triangulum 7.0 2590 M34 OC Perseus 6.0 1.4 M35 OC Gemini 5.5 2.8 M36 OC Auriga 6.5 4.1 M37 OC Auriga 6.0 4.6 M38 OC Auriga 7.0 4.2 M39 OC Cygnus 5.5 0.3 M40 Winnecke 4 DS Ursa Major 9.0 M41 OC Canis
    [Show full text]
  • Making a Sky Atlas
    Appendix A Making a Sky Atlas Although a number of very advanced sky atlases are now available in print, none is likely to be ideal for any given task. Published atlases will probably have too few or too many guide stars, too few or too many deep-sky objects plotted in them, wrong- size charts, etc. I found that with MegaStar I could design and make, specifically for my survey, a “just right” personalized atlas. My atlas consists of 108 charts, each about twenty square degrees in size, with guide stars down to magnitude 8.9. I used only the northernmost 78 charts, since I observed the sky only down to –35°. On the charts I plotted only the objects I wanted to observe. In addition I made enlargements of small, overcrowded areas (“quad charts”) as well as separate large-scale charts for the Virgo Galaxy Cluster, the latter with guide stars down to magnitude 11.4. I put the charts in plastic sheet protectors in a three-ring binder, taking them out and plac- ing them on my telescope mount’s clipboard as needed. To find an object I would use the 35 mm finder (except in the Virgo Cluster, where I used the 60 mm as the finder) to point the ensemble of telescopes at the indicated spot among the guide stars. If the object was not seen in the 35 mm, as it usually was not, I would then look in the larger telescopes. If the object was not immediately visible even in the primary telescope – a not uncommon occur- rence due to inexact initial pointing – I would then scan around for it.
    [Show full text]