DOCSLIB.ORG

UI) Existential Instantiation (EI

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
UI) Existential Instantiation (EI Existential instantiation (EI) For any sentence α, variable v, and constant symbol k that does not appear elsewhere in the knowledge base: Inference in first-order logic ∃ v α Subst({v/k}, α) E.g., ∃ x Crown(x) ∧ OnHead(x, John) yields Chapter 9 Crown(C1) ∧ OnHead(C1, John) provided C1 is a new constant symbol, called a Skolem constant Another example: from ∃ x d(xy)/dy = xy we obtain d(ey)/dy = ey provided e is a new constant symbol Chapter 9 1 Chapter 9 4 Outline Existential instantiation contd. ♦ Reducing first-order inference to propositional inference UI can be applied several times to add new sentences; the new KB is logically equivalent to the old ♦ Unification EI can be applied once to replace the existential sentence; ♦ Generalized Modus Ponens the new KB is not equivalent to the old, ♦ Forward and backward chaining but is satisfiable iff the old KB was satisfiable ♦ Resolution Chapter 9 2 Chapter 9 5 Universal instantiation (UI) Reduction to propositional inference Every instantiation of a universally quantified sentence is entailed by it: Suppose the KB contains just the following: ∀ v α ∀ x King(x) ∧ Greedy(x) ⇒ Evil(x) Subst({v/g}, α) King(John) Greedy(John) for any variable v and ground term g Brother(Richard,John) E.g., ∀ x King(x) ∧ Greedy(x) ⇒ Evil(x) yields Instantiating the universal sentence in all possible ways, we have King(John) ∧ Greedy(John) ⇒ Evil(John) King(John) ∧ Greedy(John) ⇒ Evil(John) King(Richard) ∧ Greedy(Richard) ⇒ Evil(Richard) King(Richard) ∧ Greedy(Richard) ⇒ Evil(Richard) King(F ather(John)) ∧ Greedy(F ather(John)) ⇒ Evil(F ather(John)) King(John) . Greedy(John) Brother(Richard,John) The new KB is propositionalized: proposition symbols are King(John), Greedy(John), Evil(John),King(Richard) etc. Chapter 9 3 Chapter 9 6 Reduction contd. Unification Claim: a ground sentence∗ is entailed by new KB iff entailed by original KB We can get the inference immediately if we can find a substitution θ such that King(x) and Greedy(x) match King(John) and Greedy(y) Claim: every FOL KB can be propositionalized so as to preserve entailment θ = {x/John, y/John} works Idea: propositionalize KB and query, apply resolution, return result Unify(α, β)= θ if αθ = βθ Problem: with function symbols, there are infinitely many ground terms, e.g., F ather(F ather(F ather(John))) Theorem: Herbrand (1930). If a sentence α is entailed by an FOL KB, p q θ it is entailed by a finite subset of the propositional KB Knows(John, x) Knows(John, Jane) {x/Jane} Knows(John, x) Knows(y,OJ) Idea: For n = 0 to ∞ do Knows(John, x) Knows(y, Mother(y)) create a propositional KB by instantiating with depth-n terms Knows(John, x) Knows(x,OJ) see if α is entailed by this KB Problem: works if α is entailed, loops if α is not entailed Theorem: Turing (1936), Church (1936), entailment in FOL is semidecidable Chapter 9 7 Chapter 9 10 Problems with propositionalization Unification Propositionalization seems to generate lots of irrelevant sentences. We can get the inference immediately if we can find a substitution θ E.g., from such that King(x) and Greedy(x) match King(John) and Greedy(y) ∀ x King(x) ∧ Greedy(x) ⇒ Evil(x) θ = {x/John, y/John} works King(John) Unify ∀ y Greedy(y) (α, β)= θ if αθ = βθ Brother(Richard,John) it seems obvious that Evil(John), but propositionalization produces lots of p q θ facts such as Greedy(Richard) that are irrelevant Knows(John, x) Knows(John, Jane) {x/Jane} Knows(John, x) Knows(y,OJ) {x/OJ, y/John} Knows(John, x) Knows(y, Mother(y)) Knows(John, x) Knows(x,OJ) Chapter 9 8 Chapter 9 11 Unification Unification We can get the inference immediately if we can find a substitution θ We can get the inference immediately if we can find a substitution θ such that King(x) and Greedy(x) match King(John) and Greedy(y) such that King(x) and Greedy(x) match King(John) and Greedy(y) θ = {x/John, y/John} works θ = {x/John, y/John} works Unify(α, β)= θ if αθ = βθ Unify(α, β)= θ if αθ = βθ p q θ p q θ Knows(John, x) Knows(John, Jane) Knows(John, x) Knows(John, Jane) {x/Jane} Knows(John, x) Knows(y,OJ) Knows(John, x) Knows(y,OJ) {x/OJ, y/John} Knows(John, x) Knows(y, Mother(y)) Knows(John, x) Knows(y, Mother(y)) {y/John, x/Mother(John)} Knows(John, x) Knows(x,OJ) Knows(John, x) Knows(x,OJ) Chapter 9 9 Chapter 9 12 Unification Example knowledge base contd. We can get the inference immediately if we can find a substitution θ ... it is a crime for an American to sell weapons to hostile nations: such that King(x) and Greedy(x) match King(John) and Greedy(y) θ = {x/John, y/John} works Unify(α, β)= θ if αθ = βθ p q θ Knows(John, x) Knows(John, Jane) {x/Jane} Knows(John, x) Knows(y,OJ) {x/OJ, y/John} Knows(John, x) Knows(y, Mother(y)) {y/John, x/Mother(John)} Knows(John, x) Knows(x,OJ) fail Standardizing apart eliminates overlap of variables, e.g., Knows(z17, OJ) Chapter 9 13 Chapter 9 16 Generalized Modus Ponens (GMP) Example knowledge base contd. ... it is a crime for an American to sell weapons to hostile nations: ′ ′ ′ p1 , p2 , ..., p , (p1 ∧ p2 ∧ ... ∧ p ⇒ q) American(x)∧W eapon(y)∧Sells(x,y,z)∧Hostile(z) ⇒ Criminal(x) n n where p ′θ = p θ for all i qθ i i Nono ... has some missiles ′ p1 is King(John) p1 is King(x) ′ p2 is Greedy(y) p2 is Greedy(x) θ is {x/John, y/John} q is Evil(x) qθ is Evil(John) GMP used with KB of definite clauses (exactly one positive literal) All variables assumed universally quantified Chapter 9 14 Chapter 9 17 Example knowledge base Example knowledge base contd. The law says that it is a crime for an American to sell weapons to hostile ... it is a crime for an American to sell weapons to hostile nations: nations. The country Nono, an enemy of America, has some missiles, and American(x)∧W eapon(y)∧Sells(x,y,z)∧Hostile(z) ⇒ Criminal(x) all of its missiles were sold to it by Colonel West, who is American. Nono ... has some missiles, i.e., ∃ x Owns(Nono, x) ∧ Missile(x): Owns(Nono, M1) and Missile(M1) Prove that Col. West is a criminal ... all of its missiles were sold to it by Colonel West Chapter 9 15 Chapter 9 18 Example knowledge base contd. Forward chaining algorithm ... it is a crime for an American to sell weapons to hostile nations: function FOL-FC-Ask(KB, α) returns a substitution or false American(x)∧W eapon(y)∧Sells(x,y,z)∧Hostile(z) ⇒ Criminal(x) Nono ... has some missiles, i.e., ∃ x Owns(Nono, x) ∧ Missile(x): repeat until new is empty new ←{} Owns(Nono, M1) and Missile(M1) for each sentence r in KB do ... all of its missiles were sold to it by Colonel West ( p1 ∧ . ∧ pn ⇒ q) ← Standardize-Apart(r) ′ ′ Missile(x) ∧ Owns(Nono, x) ⇒ Sells(W est, x, Nono) for each θ such that (p1 ∧ . ∧ pn)θ = (p1 ∧ . ∧ pn)θ ′ ′ Missiles are weapons: for some p1,..., pn in KB q′ ← Subst(θ, q) if q′ is not a renaming of a sentence already in KB or new then do add q′ to new φ ← Unify(q ′, α) if φ is not fail then return φ add new to KB return false Chapter 9 19 Chapter 9 22 Example knowledge base contd. Forward chaining proof ... it is a crime for an American to sell weapons to hostile nations: American(x)∧W eapon(y)∧Sells(x,y,z)∧Hostile(z) ⇒ Criminal(x) Nono ... has some missiles, i.e., ∃ x Owns(Nono, x) ∧ Missile(x): Owns(Nono, M1) and Missile(M1) ... all of its missiles were sold to it by Colonel West Missile(x) ∧ Owns(Nono, x) ⇒ Sells(W est, x, Nono) Missiles are weapons: Missile(x) ⇒ W eapon(x) An enemy of America counts as “hostile”: American(West) Missile(M1) Owns(Nono,M1) Enemy(Nono,America) Chapter 9 20 Chapter 9 23 Example knowledge base contd. Forward chaining proof ... it is a crime for an American to sell weapons to hostile nations: American(x)∧W eapon(y)∧Sells(x,y,z)∧Hostile(z) ⇒ Criminal(x) Nono ... has some missiles, i.e., ∃ x Owns(Nono, x) ∧ Missile(x): Owns(Nono, M1) and Missile(M1) ... all of its missiles were sold to it by Colonel West Missile(x) ∧ Owns(Nono, x) ⇒ Sells(W est, x, Nono) Weapon(M1) Sells(West,M1,Nono) Hostile(Nono) Missiles are weapons: Missile(x) ⇒ W eapon(x) An enemy of America counts as “hostile”: Enemy(x, America) ⇒ Hostile(x) West, who is American ... American(West) Missile(M1) Owns(Nono,M1) Enemy(Nono,America) American(W est) The country Nono, an enemy of America ... Enemy(Nono, America) Chapter 9 21 Chapter 9 24 Forward chaining proof Backward chaining example Criminal(West) Criminal(West) Weapon(M1) Sells(West,M1,Nono) Hostile(Nono) American(West) Missile(M1) Owns(Nono,M1) Enemy(Nono,America) Chapter 9 25 Chapter 9 28 Properties of forward chaining Backward chaining example Sound and complete for first-order definite clauses Criminal(West) {x/West} (proof similar to propositional proof) Datalog = first-order definite clauses + no functions (e.g., crime KB) FC terminates for Datalog in poly iterations: at most p · nk literals May not terminate in general (with functions) if α is not entailed American(x) Weapon(y) Sells(x,y,z) Hostile(z) This is unavoidable: entailment with definite clauses is semidecidable Chapter 9 26 Chapter 9 29 Backward chaining algorithm Backward chaining example function FOL-BC-Ask(KB, goals, θ) returns a set of substitutions Criminal(West) {x/West} inputs: KB, a knowledge base goals, a list of conjuncts forming a query (θ already applied) θ, the current substitution, initially the empty substitution {} local variables: answers, a set of substitutions, initially empty if goals is empty then return {θ} American(West) Weapon(y) Sells(x,y,z) Hostile(z) ′ Subst First q ← (θ, (goals)) { } for each sentence r in KB where Standardize-Apart(r) = ( p1 ∧ .
Load more

Recommended publications
  • Section 1.4: Predicate Logic
    Section 1.4: Predicate Logic January 22, 2021 Abstract We now consider the logic associated with predicate wffs, including a new set of derivation rules for demonstrating validity (the analogue of tautology in the propositional calculus) – that is, for proving theorems! 1 Derivation rules • First of all, all the rules of propositional logic still hold. Whew! Propositional wffs are simply boring, variable-less predicate wffs. • Our author suggests the following “general plan of attack”: – strip off the quantifiers – work with the separate wffs – insert quantifiers as necessary Now, how may we legitimately do so? Consider the classic syllo- gism: a. (All) Humans are mortal. b. Socrates is human. Therefore Socrates is mortal. The way we reason is that the rule “Humans are mortal” applies to the specific example “Socrates”; hence this Socrates is mortal. We might write this as a. (∀x)(H(x) → M(x)) b. H(s) Therefore M(s). It seems so obvious! But how do we justify that in a proof se- quence? • New rules for predicate logic: in the following, you should un- derstand by the symbol x in P (x) an expression with free variable x, possibly containing other (quantified) variables: e.g. P (x) ≡ (∀y)(∃z)Q(x,y,z) (1) – Universal Instantiation: from (∀x)P (x) deduce P (t). Caveat: t must not already appear as a variable in the ex- pression for P (x): in the equation above, (1), it would not do to deduce P (y) or P (z), as those variables appear in the expression (in a quantified fashion) already.
    [Show full text]
  • Logic and Proof
    CS2209A 2017 Applied Logic for Computer Science Lecture 11, 12 Logic and Proof Instructor: Yu Zhen Xie 1 Proofs • What is a theorem? – Lemma, claim, etc • What is a proof? – Where do we start? – Where do we stop? – What steps do we take? – How much detail is needed? 2 The truth 3 Theories and theorems • Theory: axioms + everything derived from them using rules of inference – Euclidean geometry, set theory, theory of reals, theory of integers, Boolean algebra… – In verification: theory of arrays. • Theorem: a true statement in a theory – Proved from axioms (usually, from already proven theorems) Pythagorean theorem • A statement can be a theorem in one theory and false in another! – Between any two numbers there is another number. • A theorem for real numbers. False for integers! 4 Axioms example: Euclid’s postulates I. Through 2 points a line segment can be drawn II. A line segment can be extended to a straight line indefinitely III. Given a line segment, a circle can be drawn with it as a radius and one endpoint as a centre IV. All right angles are congruent V. Parallel postulate 5 Some axioms for propositional logic • For any formulas A, B, C: – A ∨ ¬ – . – . – A • Also, like in arithmetic (with as +, as *) – , – Same holds for ∧. – Also, • And unlike arithmetic – ( ) 6 Counterexamples • To disprove a statement, enough to give a counterexample: a scenario where it is false – To disprove that • Take = ", = #, • Then is false, but B is true. – To disprove that if %& '( ) &, ( , then '( %& ) &, ( , • Set the domain of x and y to be {0,1} • Set P(0,0) and P(1,1) to true, and P(0,1), P(1,0) to false.
    [Show full text]
  • Philosophy 109, Modern Logic Russell Marcus
    Philosophy 240: Symbolic Logic Hamilton College Fall 2014 Russell Marcus Reference Sheeet for What Follows Names of Languages PL: Propositional Logic M: Monadic (First-Order) Predicate Logic F: Full (First-Order) Predicate Logic FF: Full (First-Order) Predicate Logic with functors S: Second-Order Predicate Logic Basic Truth Tables - á á @ â á w â á e â á / â 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 0 0 1 1 0 1 0 0 1 0 0 0 0 1 0 1 1 0 1 1 0 0 1 0 0 0 0 0 0 0 1 0 0 1 0 Rules of Inference Modus Ponens (MP) Conjunction (Conj) á e â á á / â â / á A â Modus Tollens (MT) Addition (Add) á e â á / á w â -â / -á Simplification (Simp) Disjunctive Syllogism (DS) á A â / á á w â -á / â Constructive Dilemma (CD) (á e â) Hypothetical Syllogism (HS) (ã e ä) á e â á w ã / â w ä â e ã / á e ã Philosophy 240: Symbolic Logic, Prof. Marcus; Reference Sheet for What Follows, page 2 Rules of Equivalence DeMorgan’s Laws (DM) Contraposition (Cont) -(á A â) W -á w -â á e â W -â e -á -(á w â) W -á A -â Material Implication (Impl) Association (Assoc) á e â W -á w â á w (â w ã) W (á w â) w ã á A (â A ã) W (á A â) A ã Material Equivalence (Equiv) á / â W (á e â) A (â e á) Distribution (Dist) á / â W (á A â) w (-á A -â) á A (â w ã) W (á A â) w (á A ã) á w (â A ã) W (á w â) A (á w ã) Exportation (Exp) á e (â e ã) W (á A â) e ã Commutativity (Com) á w â W â w á Tautology (Taut) á A â W â A á á W á A á á W á w á Double Negation (DN) á W --á Six Derived Rules for the Biconditional Rules of Inference Rules of Equivalence Biconditional Modus Ponens (BMP) Biconditional DeMorgan’s Law (BDM) á / â -(á / â) W -á / â á / â Biconditional Modus Tollens (BMT) Biconditional Commutativity (BCom) á / â á / â W â / á -á / -â Biconditional Hypothetical Syllogism (BHS) Biconditional Contraposition (BCont) á / â á / â W -á / -â â / ã / á / ã Philosophy 240: Symbolic Logic, Prof.
    [Show full text]
  • Predicate Logic
    Predicate Logic Andreas Klappenecker Predicates A function P from a set D to the set Prop of propositions is called a predicate. The set D is called the domain of P. Example Let D=Z be the set of integers. Let a predicate P: Z -> Prop be given by P(x) = x>3. The predicate itself is neither true or false. However, for any given integer the predicate evaluates to a truth value. For example, P(4) is true and P(2) is false Universal Quantifier (1) Let P be a predicate with domain D. The statement “P(x) holds for all x in D” can be written shortly as ∀xP(x). Universal Quantifier (2) Suppose that P(x) is a predicate over a finite domain, say D={1,2,3}. Then ∀xP(x) is equivalent to P(1)⋀P(2)⋀P(3). Universal Quantifier (3) Let P be a predicate with domain D. ∀xP(x) is true if and only if P(x) is true for all x in D. Put differently, ∀xP(x) is false if and only if P(x) is false for some x in D. Existential Quantifier The statement P(x) holds for some x in the domain D can be written as ∃x P(x) Example: ∃x (x>0 ⋀ x2 = 2) is true if the domain is the real numbers but false if the domain is the rational numbers. Logical Equivalence (1) Two statements involving quantifiers and predicates are logically equivalent if and only if they have the same truth values no matter which predicates are substituted into these statements and which domain is used.
    [Show full text]
  • Chapter 4, Propositional Calculus
    ECS 20 Chapter 4, Logic using Propositional Calculus 0. Introduction to Discrete Mathematics. 0.1. Discrete = Individually separate and distinct as opposed to continuous and capable of infinitesimal change. Integers vs. real numbers, or digital sound vs. analog sound. 0.2. Discrete structures include sets, permutations, graphs, trees, variables in computer programs, and finite-state machines. 0.3. Five themes: logic and proofs, discrete structures, combinatorial analysis, induction and recursion, algorithmic thinking, and applications and modeling. 1. Introduction to Logic using Propositional Calculus and Proof 1.1. “Logic” is “the study of the principles of reasoning, especially of the structure of propositions as distinguished from their content and of method and validity in deductive reasoning.” (thefreedictionary.com) 2. Propositions and Compound Propositions 2.1. Proposition (or statement) = a declarative statement (in contrast to a command, a question, or an exclamation) which is true or false, but not both. 2.1.1. Examples: “Obama is president.” is a proposition. “Obama will be re-elected.” is not a proposition. 2.1.2. “This statement is false.” is a paradox that many would not consider a proposition. 2.1.3. For ECS 20, we will use p, q, and r to symbolize propositions, subpropositions, or logical variables which take true or false values. 2.2. Compound Proposition = a proposition that has its truth value completely determined by the truth values of two or more subpropositions and the operators (also called connectives) connecting them. 3. Basic Logical Operations 3.1. Conjunction = = “and.” If both p and q are true, then p q is true, otherwise p q is false.
    [Show full text]
  • Formal Logic: Quantifiers, Predicates, and Validity
    Formal Logic: Quantifiers, Predicates, and Validity CS 130 – Discrete Structures Variables and Statements • Variables: A variable is a symbol that stands for an individual in a collection or set. For example, the variable x may stand for one of the days. We may let x = Monday, x = Tuesday, etc. • We normally use letters at the end of the alphabet as variables, such as x, y, z. • A collection of objects is called the domain of objects. For the above example, the days in the week is the domain of variable x. CS 130 – Discrete Structures 55 Quantifiers • Propositional wffs have rather limited expressive power. E.g., “For every x, x > 0”. • Quantifiers: Quantifiers are phrases that refer to given quantities, such as "for some" or "for all" or "for every", indicating how many objects have a certain property. • Two kinds of quantifiers: – Universal Quantifier: represented by , “for all”, “for every”, “for each”, or “for any”. – Existential Quantifier: represented by , “for some”, “there exists”, “there is a”, or “for at least one”. CS 130 – Discrete Structures 56 Predicates • Predicate: It is the verbal statement which describes the property of a variable. Usually represented by the letter P, the notation P(x) is used to represent some unspecified property or predicate that x may have. – P(x) = x has 30 days. – P(April) = April has 30 days. – What is the truth value of (x)P(x) where x is all the months and P(x) = x has less than 32 days • Combining the quantifier and the predicate, we get a complete statement of the form (x)P(x) or (x)P(x) • The collection of objects is called the domain of interpretation, and it must contain at least one object.
    [Show full text]
  • How to Adopt a Logic
    How to adopt a logic Daniel Cohnitz1 & Carlo Nicolai2 1Utrecht University 2King’s College London Abstract What is commonly referred to as the Adoption Problem is a challenge to the idea that the principles of logic can be rationally revised. The argument is based on a reconstruction of unpublished work by Saul Kripke. As the reconstruction has it, Kripke essentially extends the scope of Willard van Orman Quine’s regress argument against conventionalism to the possibility of adopting new logical principles. In this paper we want to discuss the scope of this challenge. Are all revisions of logic subject to the regress problem? If not, are there interesting cases of logical revision that are subject to the regress problem? We will argue that both questions should be answered negatively. 1 Introduction What is commonly referred to as the Adoption Problem1 is often considered a challenge to the idea that the principles for logic can be rationally revised. The argument is based on a reconstruction of unpublished work by Saul Kripke.2 As the reconstruction has it, Kripke essentially extends the scope of William van Orman Quine’s regress argument (Quine, 1976) against conventionalism to the possibility of adopting new logical principles or rules. According to the reconstruction, the Adoption Problem is that new logical rules cannot be adopted unless one already can infer with these rules, in which case the adoption of the rules is unnecessary (Padro, 2015, 18). In this paper we want to discuss the scope of this challenge. Are all revisions of logic subject to the regress problem? If not, are there interesting cases of logical revision that are subject to the regress problem? We will argue that both questions should be answered negatively.
    [Show full text]
  • The Logic of Quantified Statements the Logic of Quantified Statements
    CHAPTER 3 THE LOGIC OF QUANTIFIED STATEMENTS Copyright © Cengage Learning. All rights reserved. SECTION 3.4 Arguments with Quantified Statements Copyright © Cengage Learning. All rights reserved. Arguments with Quantified Statements The rule of universal instantiation (in-stan-she-AY-shun) says the following: Universal instantiation is the fundamental tool of deductive reasoning. Mathematical formulas, definitions, and theorems are like general templates that are used over and over in a wide variety of particular situations. 3 Arguments with Quantified Statements A given theorem says that such and such is true for all things of a certain type. If, in a given situation, you have a particular object of that type, then by universal instantiation, you conclude that such and such is true for that particular object. You may repeat this process 10, 20, or more times in a single proof or problem solution. 4 Universal Modus Ponens 5 Universal Modus Ponens The rule of universal instantiation can be combined with modus ponens to obtain the valid form of argument called universal modus ponens . 6 Universal Modus Ponens Note that the first, or major, premise of universal modus ponens could be written “All things that make P(x) true make Q(x) true,” in which case the conclusion would follow by universal instantiation alone. However, the if-then form is more natural to use in the majority of mathematical situations. 7 Example 1 – Recognizing Universal Modus Ponens Rewrite the following argument using quantifiers, variables, and predicate symbols. Is this argument valid? Why? If an integer is even, then its square is even.
    [Show full text]
  • A Concise Introduction to Logic Craig Delancey SUNY Oswego
    SUNY Geneseo KnightScholar Open SUNY Textbooks Open Educational Resources 2017 A Concise Introduction to Logic Craig DeLancey SUNY Oswego Follow this and additional works at: https://knightscholar.geneseo.edu/oer-ost Part of the Philosophy Commons This work is licensed under a Creative Commons Attribution-Noncommercial-Share Alike 4.0 License. Recommended Citation DeLancey, Craig, "A Concise Introduction to Logic" (2017). Open SUNY Textbooks. 4. https://knightscholar.geneseo.edu/oer-ost/4 This Book is brought to you for free and open access by the Open Educational Resources at KnightScholar. It has been accepted for inclusion in Open SUNY Textbooks by an authorized administrator of KnightScholar. For more information, please contact [email protected]. A Concise Introduction to Logic A Concise Introduction to Logic Craig DeLancey Open SUNY Textbooks © 2017 Craig DeLancey ISBN: 978-1-942341-42-0 ebook 978-1-942341-43-7 print This publication was made possible by a SUNY Innovative Instruction Technology Grant (IITG). IITG is a competitive grants program open to SUNY faculty and support staff across all disciplines. IITG encourages development of innovations that meet the Power of SUNY’s transformative vision. Published by Open SUNY Textbooks Milne Library State University of New York at Geneseo Geneseo, NY 14454 This book was produced using Pressbooks.com, and PDF rendering was done by PrinceXML. A Concise Introduction to Logic by Craig DeLancey is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted. Dedication For my mother Contents About the Textbook Reviewer's Notes Adam Kovach 0. Introduction 1 Part I: Propositional Logic 1.
    [Show full text]
  • Vagueness and the Logic of the World
    University of Nebraska - Lincoln DigitalCommons@University of Nebraska - Lincoln Philosophy Dissertations, Theses, & Student Research Philosophy, Department of Spring 4-19-2020 Vagueness and the Logic of the World Zack Garrett University of Nebraska - Lincoln, [email protected] Follow this and additional works at: https://digitalcommons.unl.edu/philosophydiss Part of the Metaphysics Commons, and the Philosophy of Language Commons Garrett, Zack, "Vagueness and the Logic of the World" (2020). Philosophy Dissertations, Theses, & Student Research. 13. https://digitalcommons.unl.edu/philosophydiss/13 This Article is brought to you for free and open access by the Philosophy, Department of at DigitalCommons@University of Nebraska - Lincoln. It has been accepted for inclusion in Philosophy Dissertations, Theses, & Student Research by an authorized administrator of DigitalCommons@University of Nebraska - Lincoln. VAGUENESS AND THE LOGIC OF THE WORLD by Zack Garrett A DISSERTATION Presented to the Faculty of The Graduate College at the University of Nebraska In Partial Fulfillment of Requirements For the Degree of Doctor of Philosophy Major: Philosophy Under the Supervision of Professor Reina Hayaki Lincoln, Nebraska May, 2020 VAGUENESS AND THE LOGIC OF THE WORLD Zack Garrett, Ph.D. University of Nebraska, 2020 Advisor: Reina Hayaki In this dissertation, I argue that vagueness is a metaphysical phenomenon—that properties and objects can be vague—and propose a trivalent theory of vagueness meant to account for the vagueness in the world. In the first half, I argue against the theories that preserve classical logic. These theories include epistemicism, con- textualism, and semantic nihilism. My objections to these theories are independent of considerations of the possibility that vagueness is a metaphysical phenomenon.
    [Show full text]
  • Nested Quantifiers and Rules of Inference
    PK 1.5 & 1.6 Nested Quantifiers and Rules of Inference By: Emily B and David R What Are Nested ● They are quantifiers within the scope of another quantifier. Quantifiers?? ● ∀x∃y(x + y = 0) ⇔ ∀xQ(x), where Q(x) = ∃y(x + y = 0). ● They come, but are not limited, in the following flavors: ○ ∀x ∀yQ(x,y) ○ ∀x ∃yQ(x,y) ○ ∃x ∀yQ(x,y) ○ ∃x ∃yQ(x,y) ○ ∀x ∀y ∃zQ(x,y,z) ○ Yada yada yada Order Matters! ● In all cases unless the type of quantification are the same ○ ∀x ∀yQ(x,y) ⇔ ∀y ∀xQ(x,y) ○ ∃x ∃yQ(x,y) ⇔ ∃y ∃xQ(x,y) ● Other than that, the order of quantifiers will affect the truth of the quantification ○ ∀x ∃yQ(x,y) != ∃y ∀xQ(x,y) ● Can be thought of as loops with the left most quantifier being the outer loop until the rightmost inner loop. ○ For example, in ∀x∃y(x + y = 0), you would loop through ALL the elements in the domain for x, searching for AT LEAST one element for y that satisfies the statement. ○ In ∃x∀yQ(x,y), you would loop through the domain, testing Work? every x until you find ONE x that satisfies the statement for ALL y How Do They A neat observation: ● After going through some observations, the book concludes that: ○ if ∃y∀xP(x, y) is true, then ∀x∃yP(x, y) must also be true ○ However, if ∀x∃yP(x, y) is true, it is not necessary for ∃y∀xP(x, y) to be true Table on how to read these quantifications Turning Sentences into Logical Expressions ● “The sum of two positive integers is always positive” x & y ϵ Z.
    [Show full text]
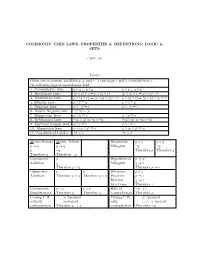
  • Commonly Used Laws, Properties & Definitions
    COMMONLY USED LAWS, PROPERTIES & DEFINITIONS: LOGIC & SETS CMSC 250 Logic Given any statement variables p, q, and r, a tautology t and a contradiction c, the following logical equivalences hold: 1. Commutative laws: p ^ q ≡ q ^ p p _ q ≡ q _ p 2. Associative laws: (p ^ q) ^ r ≡ p ^ (q ^ r) (p _ q) _ r ≡ p _ (q _ r) 3. Distributive laws: p ^ (q _ r) ≡ (p ^ q) _ (p ^ r) p _ (q ^ r) ≡ (p _ q) ^ (p _ r) 4. Identity laws: p ^ t ≡ p p _ c ≡ p 5. Negation laws: p _:p ≡ t p ^ :p ≡ c 6. Double Negative law: :(:p) ≡ p 7. Idempotent laws: p ^ p ≡ p p _ p ≡ p 8. DeMorgan's laws: :(p ^ q) ≡ :p _:q :(p _ q) ≡ :p ^ :q 9. Universal bounds laws: p _ t ≡ t p ^ c ≡ c 10. Absorption laws: p _ (p ^ q) ≡ p p ^ (p _ q) ≡ p 11. Negations of t and c: :t ≡ c :c ≡ t Modus Ponens Modus Tollens Disjunctive p _ q p _ q p ! q p ! q Syllogism :q :p p :q Therefore p Therefore q Therefore q Therefore :p Conjunctive p Hypothetical p ! q Addition q Syllogism q ! r Therefore p ^ q Therefore p ! r Disjunctive p q Dilemma: p _ q Addition Therefore p _ q Therefore p _ q Proof by p ! r Division q ! r into Cases Therefore r Conjunctive p ^ q p ^ q Rule of :p ! c Simplification Therefore p Therefore q Contradiction Therefore p Closing C.W. jp Assumed Closing C.W.
    [Show full text]