DOCSLIB.ORG

Symbol Index

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Symbol Index Cambridge University Press 978-0-521-13170-4 - Fundamentals of Error-Correcting Codes W. Cary Huffman and Vera Pless Index More information Symbol index ⊥,5,275 Aq (n, d,w), 60 n ⊥H ,7 A (F), 517 , 165 Aut(P, B), 292 , 533 Bi (C), 75 a , p , 219 B(n d), 48 (g(x)), 125 Bq (n, d), 48 g(x) , 125, 481 B(G), 564 x, y ,7 B(t, m), 439 x, y T , 383 C1 ⊕ C2,18 αq (δ), 89, 541 C1 C2, 368 Aut(C), 26, 384 Ci /C j , 353 AutPr(C), 28 Ci ⊥C j , 353 (L, G), 521 C∗,13 μ, 187 C| , 116 Fq (n, k), 567 Cc, 145 (q), 426 C,14 2, 423 C(L), 565 ⊥ 24, 429 C ,5,469 ∗ ⊥ , 424 C H ,7 C ⊥ ( ), 427 C T , 384 C 4( ), 503 Cq (A), 308 x, y ( ), 196 Cs , 114, 122 λ i , 293 CT ,14 λ j i , 295 CT ,16 λ i (x), 609 C(X , P, D), 535 μ a , 138 d2m , 367 ν C ( ), 465 d free, 563 ν P ( ), 584 dr (C), 283 ν s , s ( i j ), 584 Dq (A), 309 π (n) C, i (x), 608, 610 d( x), 65 ρ(C), 50, 432 d(x, y), 7 , ρBCH(t, m), 440 dE (x y), 470 , ρRM(r, m), 437 dH (x y), 470 , σp, 111 dL (x y), 470 σ (x), 181 deg f (x), 101 σ (μ)(x), 187 det , 423 Dext φs , 164 , 249 φs : Fq [I] → I, 164 e7, 367 ω(x), 190 e8, 367 A , 309 E8, 428 T A ,4 Eb, 577 E Ai (C), 8, 252 n, 209 A(n, d), 48 Es , 573 Aq (n, d), 48 evP , 534 © in this web service Cambridge University Press www.cambridge.org Cambridge University Press 978-0-521-13170-4 - Fundamentals of Error-Correcting Codes W. Cary Huffman and Vera Pless Index More information 631 Symbol index extdeg G, 558 mC, 368 F2,3 N0, 575 F3,3 N 16,68 F4,3 na (x), 470 k F9, 243 (n, 2 , d), 383 F16, 184 (n, c, r), 598 Fq ,2,100 (n, k, m), 561 Fn , , , q ,3 (n k m d), 563 Fq [x], 101 (n, M, d), 53 F[x1,...,xn], 519 N p, 237 H f , 519 Ns (δ), 195 fn, 373 N(v), 426 f (x) | g(x), 102 ordn(q), 122 G6,7 PAut(C), 22, 469 G11,33 (P, B), 291 G12,32 Pb, 578 G23,32 Perr,46 s G24,31 PG(2, 2 ), 319 g24, 374 PG(r − 1, q), 29 GA1(I), 165 PGL2(q), 422 GA3(2), 368 Pk , 174 Gal(Fq ), 112 P(r + 1), 515 Gal(Fq : Fpr ), 112 prob(E1), 39 G(C), 371 prob(E1 | E2), 39 G0(C), 372 Pr(v), 407 G1(C), 372 PSL2(7), 22, 368 G2(C), 371 PSL2(23), 402 G(C), 472 Qp, 237 gcd( f (x), g(x)), 102 Res(C), 496 GF(q), 2, 100 Res(C, c), 80 r GR(4 ), 505 Resγi f , 524 GRSk (γ, v), 176, 196, 520 Rn, 121, 124, 209 H3,5 Rn, 480 H3,6 R(r, m), 34 Hr ,29 Rq (r, m), 524 H2,r ,29 Rt , 577 H3,2,6 span{x, y}, 275 Hq,r ,29 S(q), 420 Hq (x), 90 S(r,ν), 256 HamC (x, y), 470 Sr (u), 40 i2, 367 S(t, k,v), 291 I (C, t), 203 supp(c), 120 intdeg G, 559 supp(D), 283 Jv, 309 Symn,21 j(x), 209 tq (n, k), 447 K(r + 1), 509 Tor(C), 496 n,q T R Kk (x), 75, 256 ( ), 506 L(D), 534 TRr , 508 Lk−1, 520 Trt , 119 q (m, r), 447 Trt (C), 119 LeeC (x,y), 448 Vq (n, a), 74 M12, 419 WC (x), 255 M23, 402 WC (x, y), 255 M24, 402 wt(x), 8 MAut(C), 26, 469 wtE (x), 470 MAutPr(C), 28 wtH (x), 470 © in this web service Cambridge University Press www.cambridge.org Cambridge University Press 978-0-521-13170-4 - Fundamentals of Error-Correcting Codes W. Cary Huffman and Vera Pless Index More information 632 Symbol index wtL (x), 470 x⊥y, 275 X 1 ∩ X 2, 531 x ∩ y,8 X f (F), 526 x · y,6,469 x j (i), 587 Zq ,76 © in this web service Cambridge University Press www.cambridge.org Cambridge University Press 978-0-521-13170-4 - Fundamentals of Error-Correcting Codes W. Cary Huffman and Vera Pless Index More information Subject index a priori term, 609 Meggitt Decoding, 158–160 α notation, 608 Message Passing Decoding, 595 A-plane, 275 Permutation Decoding, 402, 403 acceptable coordinate, 451 Peterson–Gorenstein–Zierler Decoding, 179, 182 Adams Bound, 455 Soft Decision Viterbi Decoding, 580, 581, 612 additive code over F4, 383 Sudan–Guruswami Decoding, 195, 196 automorphism group, 384 Sugiyama Decoding, 190, 191 Balance Principle, 387 Sum-Product Decoding, 602 dodecacode, 388 Syndrome Decoding, 42, 43 equivalent, 384 Turbo Decoding, 610 generator matrix, 383 Two-Way a Posteriori Probability (APP) Decoding, hexacode, 383 587, 592 mass formula, 386 Viterbi Decoding, 551, 556 trace dual, 384 amalgamated direct sum (ADS), 452 trace inner product, 383 ancestor, 460 trace self-dual, 384 APP, 587 trace self-orthogonal, 384 Assmus–Mattson Theorem, 303 Type I, 385 asymptotic bound, 88 extremal, 386 Elias, 93 Type II, 385 First MRRW, 94 extremal, 386 Gilbert–Varshamov, 94, 541 Gleason’s Theorem, 385 exceeded by algebraic geometry codes, 544 additive white Gaussian noise (AWGN), 575 met by Goppa codes, 542 adjoining a root, 108 Hamming, 92 affine group, 165, 251, 366, 368 Plotkin, 89 affine plane curve, 526 Second MRRW, 94 affine space, 517 Singleton, 89 affine-invariant code, 162, 165 Tsfasman–Vl˘adut¸–Zink, 544 extended BCH, 172 asymptotically bad code, 173, 541 AG, 535 asymptotically good code, 173, 542 algebraic geometry (AG) code C(X , P, D), 535 automorphism group, 22, 26, 384 dimension, 535 monomial, 26, 469 dual, 541 of a design, 292 exceed Asymptotic Gilbert–Varshamov Bound, 544 permutation, 22, 469 generalized Reed–Solomon code as, 537 transitive, 23, 28, 271, 308 generator matrix, 535 automorphism of a design, 292 minimum distance, 535 automorphism of a field, 111 Reed–Solomon code as, 536 fixed element, 112 algorithm Frobenius, 112 Berlekamp–Massey Decoding, 186, 188 Galois group, 112 Classification, 366 AWGN, 575 Division, 102 Euclidean, 102 Balance Principle, 351, 379, 387 Gallager Hard Decision Decoding, 599 bandwidth, 577 General Viterbi, 584, 586 basic generator matrix, 559 © in this web service Cambridge University Press www.cambridge.org Cambridge University Press 978-0-521-13170-4 - Fundamentals of Error-Correcting Codes W. Cary Huffman and Vera Pless Index More information 634 Subject index basis of minimum weight codewords, 83, 85 Plotkin, 58 BCH Bound, 151 Redundancy, 433 BCH code, 168 Singleton, 71 Berlekamp–Massey Decoding Algorithm, 186, 188 Sphere Covering, 434 Bose distance, 171 Sphere Packing, 48, 59, 74 covering radius, 440, 441, 443, 444 Square Root, 230 designed distance, 168 Supercode Lemma, 434 dimension, 170 van Lint–Wilson Bounding Technique, 154 minimum distance, 171 Varshamov, 88 narrow-sense, 168, 521 BPSK, 573 nested, 169 Bruck–Ryser–Chowla Theorem, 319 Peterson–Gorenstein–Zierler Decoding Algorithm, BSC, 39 179, 182 burst, 202 primitive, 168 byte, 202 affine-invariant extension, 172 Reed–Solomon code, see Reed–Solomon code Calderbank Bound, 457 Sugiyama Decoding Algorithm, 190, 191 canonical generator matrix, 558 BER, 578 Cassini, 602, 614 Berlekamp–Massey Decoding Algorithm, 186, 188 catastrophic generator matrix, 569 B´ezout’s Theorem, 531 CCSDS, 612 Big Viterbi Decoder, 613 CD, 203 binary adder, 129 Challenger, 613 binary field, 3 channel, 1, 573 binary phase-shift keying (BPSK), 573 binary symmetric, 39, 583 binary symmetric channel (BSC), 39, 583 capacity of, 1, 47, 577 crossover probability of, 39, 583 discrete memoryless, 39 bit, 202 noisy, 1 bit error rate (BER), 578 statistics, 576, 587 block, 291 channel capacity, 1, 47, 577 bordered circulant matrix, 31, 376 characteristic, 100 bordered reverse circulant matrix, 377 child, 358, 375, 460 bound, 48 CIRC, 204 Aq (n, d), 48 circulant matrix, 376 Aq (n, d,w), 60 Classification Algorithm, 366 Bq (n, d), 48 classification problem, 365 Adams, 455 clock cycle, 129, 549, 573 asymptotic, see asymptotic bound code, 3 BCH, 151 additive, see additive code over F4 Calderbank, 457 affine-invariant, see affine-invariant code Delsarte, 440 algebraic geometry, see algebraic geometry (AG) Elias, 74 code Generalized Griesmer, 287 asymptotically bad, 173, 541 Generalized Singleton, 286 asymptotically good, 173, 542 Gilbert, 86 automorphism group, 26 Griesmer, 81 BCH, see BCH code Hamming, 48 binary, 3 Hartmann–Tzeng, 153 block, 546 Hou, 458 bordered double circulant construction, 376 Johnson, 65, 74 bordered double circulant generator matrix, 376 restricted, 61 bordered reverse circulant construction, 377 unrestricted, 63 bordered reverse circulant generator matrix, 377 Linear Programming, 78 burst error-correcting, 202 meet, 53 complement of, 145 MRRW, 94 component, 370 Norse, 435 concatenated, 201 on maximum distance separable code, 264 constant weight, 60, 282 © in this web service Cambridge University Press www.cambridge.org Cambridge University Press 978-0-521-13170-4 - Fundamentals of Error-Correcting Codes W. Cary Huffman and Vera Pless Index More information 635 Subject index convolutional, see convolutional code normal, 452 covering radius of, see covering radius odd-like, 12, 210 cyclic, see cyclic code optimal, 53 decomposable, 368 orthogonal, 5 direct sum, 18 orthogonal sum, 276 weight enumerator of, 255 outer, 201 divisible, 11 packing radius of, 41 divisor of, 11, 86, 157 parallel concatenated convolutional, 604 double circulant construction, 376 parity check matrix, 4 double circulant generator matrix, 132, 376 perfect, 48, 49 doubly-even, 12, 150, 361 permutation automorphism group, 22 duadic, see duadic code permutation equivalent, 20 dual, 5, 469 Pless symmetry, see Pless symmetry code equivalent, 25 Preparata, see Preparata code even, 11 punctured, 13 even-like, 12, 210 quadratic residue, see quadratic residue code extended, 14 quasi-cyclic, 131 extremal, 346 quasi-perfect, 50 formally self-dual, see formally self-dual code quaternary, 3 generalized Hamming weight, see generalized quick-look-in, 612 Hamming weight rate of, 47 generator matrix, 4 redundancy set, 4 standard form of, 4, 21 Reed–Muller, see Reed–Muller code Golay, binary, see Golay codes, binary Reed–Solomon, see Reed–Solomon code Golay, ternary, see Golay codes, ternary repetition, 4 Goppa, see Goppa code replicated, 390 Hamming, see Hamming code residual, 80 Hermitian self-dual, see Hermitian self-dual
Load more

Recommended publications
  • Scribe Notes
    6.440 Essential Coding Theory Feb 19, 2008 Lecture 4 Lecturer: Madhu Sudan Scribe: Ning Xie Today we are going to discuss limitations of codes. More specifically, we will see rate upper bounds of codes, including Singleton bound, Hamming bound, Plotkin bound, Elias bound and Johnson bound. 1 Review of last lecture n k Let C Σ be an error correcting code. We say C is an (n, k, d)q code if Σ = q, C q and ∆(C) d, ⊆ | | | | ≥ ≥ where ∆(C) denotes the minimum distance of C. We write C as [n, k, d]q code if furthermore the code is a F k linear subspace over q (i.e., C is a linear code). Define the rate of code C as R := n and relative distance d as δ := n . Usually we fix q and study the asymptotic behaviors of R and δ as n . Recall last time we gave an existence result, namely the Gilbert-Varshamov(GV)→ ∞ bound constructed by greedy codes (Varshamov bound corresponds to greedy linear codes). For q = 2, GV bound gives codes with k n log2 Vol(n, d 2). Asymptotically this shows the existence of codes with R 1 H(δ), which is similar≥ to− Shannon’s result.− Today we are going to see some upper bound results, that≥ is,− code beyond certain bounds does not exist. 2 Singleton bound Theorem 1 (Singleton bound) For any code with any alphabet size q, R + δ 1. ≤ Proof Let C Σn be a code with C Σ k. The main idea is to project the code C on to the first k 1 ⊆ | | ≥ | | n k−1 − coordinates.
    [Show full text]
  • Fundamentals of Error-Correcting Codes W
    Cambridge University Press 978-0-521-13170-4 - Fundamentals of Error-Correcting Codes W. Cary Huffman and Vera Pless Frontmatter More information Fundamentals of Error-Correcting Codes Fundamentals of Error-Correcting Codes is an in-depth introduction to coding theory from both an engineering and mathematical viewpoint. As well as covering classical topics, much coverage is included of recent techniques that until now could only be found in special- ist journals and book publications. Numerous exercises and examples and an accessible writing style make this a lucid and effective introduction to coding theory for advanced undergraduate and graduate students, researchers and engineers, whether approaching the subject from a mathematical, engineering, or computer science background. Professor W. Cary Huffman graduated with a PhD in mathematics from the California Institute of Technology in 1974. He taught at Dartmouth College and Union College until he joined the Department of Mathematics and Statistics at Loyola in 1978, serving as chair of the department from 1986 through 1992. He is an author of approximately 40 research papers in finite group theory, combinatorics, and coding theory, which have appeared in journals such as the Journal of Algebra, IEEE Transactions on Information Theory, and the Journal of Combinatorial Theory. Professor Vera Pless was an undergraduate at the University of Chicago and received her PhD from Northwestern in 1957. After ten years at the Air Force Cambridge Research Laboratory, she spent a few years at MIT’s project MAC. She joined the University of Illinois-Chicago’s Department of Mathematics, Statistics, and Computer Science as a full professor in 1975 and has been there ever since.
    [Show full text]
  • Optimal Codes and Entropy Extractors
    Department of Mathematics Ph.D. Programme in Mathematics XXIX cycle Optimal Codes and Entropy Extractors Alessio Meneghetti 2017 University of Trento Ph.D. Programme in Mathematics Doctoral thesis in Mathematics OPTIMAL CODES AND ENTROPY EXTRACTORS Alessio Meneghetti Advisor: Prof. Massimiliano Sala Head of the School: Prof. Valter Moretti Academic years: 2013{2016 XXIX cycle { January 2017 Acknowledgements I thank Dr. Eleonora Guerrini, whose Ph.D. Thesis inspired me and whose help was crucial for my research on Coding Theory. I also thank Dr. Alessandro Tomasi, without whose cooperation this work on Entropy Extraction would not have come in the present form. Finally, I sincerely thank Prof. Massimiliano Sala for his guidance and useful advice over the past few years. This research was funded by the Autonomous Province of Trento, Call \Grandi Progetti 2012", project On silicon quantum optics for quantum computing and secure communications - SiQuro. i Contents List of Figures......................v List of Tables....................... vii Introduction1 I Codes and Random Number Generation7 1 Introduction to Coding Theory9 1.1 Definition of systematic codes.............. 16 1.2 Puncturing, shortening and extending......... 18 2 Bounds on code parameters 27 2.1 Sphere packing bound.................. 29 2.2 Gilbert bound....................... 29 2.3 Varshamov bound.................... 30 2.4 Singleton bound..................... 31 2.5 Griesmer bound...................... 33 2.6 Plotkin bound....................... 34 2.7 Johnson bounds...................... 36 2.8 Elias bound........................ 40 2.9 Zinoviev-Litsyn-Laihonen bound............ 42 2.10 Bellini-Guerrini-Sala bounds............... 43 iii 3 Hadamard Matrices and Codes 49 3.1 Hadamard matrices.................... 50 3.2 Hadamard codes..................... 53 4 Introduction to Random Number Generation 59 4.1 Entropy extractors...................
    [Show full text]
  • Study of Some Bounds on Binary Codes
    5 X October 2017 http://doi.org/10.22214/ijraset.2017.10004 International Journal for Research in Applied Science & Engineering Technology (IJRASET) ISSN: 2321-9653; IC Value: 45.98; SJ Impact Factor:6.887 Volume 5 Issue X, October 2017- Available at www.ijraset.com Study of Some Bounds on Binary Codes Rajiv Jain1, Jaskarn Singh Bhullar2 1,2Department of Applied Sciences, MIMIT, Malout Punjab Abstract: In this paper, various bounds on maximum number of codeword’s for a given size and minimum distance is discussed. Then these bounds are studied with example and various types of upper bounds are calculated for size and distance. The comparison of these bounds have been done and the tighter bounds for (,) is discussed. Keywords: Error Correction, Binary Codes, Bounds, Hamming Bound, Plot kin Bound, Elias Bound I. INTRODUCTION For a given q-ary (n, M, d) error correcting code, n is the size of code, d is the minimum distance between codewords of the code and M is the maximum number of codewords in the code. The efficiency of error correcting code is measured by number of codewords M in the code and the d is the error correcting capability of the code[1, 5]. It is necessary to have maximum number of codewords M in code with minimum distance d as high as possible for a good error correcting code. But in practice, for a code of given size n and minimum distance d, it is not always possible to obtain large M. So for given n, one has to negotiate between number of codewords M and Minimum distance d.
    [Show full text]
  • Super-Visible Codes
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Elsevier - Publisher Connector Discrete Mathematics 110 (1992) 119-134 119 North-Holland Super-visible codes J. Francke and J.J.H. Meijers Department of Mathematics and Computing Science, Eindhouen University of Technology, Eindhoven, Netherlands Received 14 August 1990 Abstract Francke, J. and J.J.H. Meijers, Super-visible codes, Discrete Mathematics 110 (1992) 119-134. Upper bounds and constructions are given for super-visible codes. These are linear codes with the property that all words of minimum weight form a basis of the code. Optimal super-visible codes are summarized for small lengths and minimum distances. 1. Introduction It is well know that the weight of a nonzero codeword in any Reed-Muller code is at least equal to the weight of the lowest-weight row of the standard generator matrix for that code. This recently led Ward [8] to study general linear codes with the same property, i.e. codes for which there exists a generator matrix G such that no nonzero codeword has smaller weight than the lowest-weight row of G. He called such codes visible. In a similar vein is the remarkable fact that the rows of the incidence matrix of a projective plane of order n =2 (mod4) generate a code of dimension $(n’+ it + 2) in which the plane is still ‘visible’ as the collection of minimum- weight codewords [l]. In general we can consider binary codes for which the words of minimum weight contain a basis of the code.
    [Show full text]
  • On the Griesmer Bound for Nonlinear Codes Emanuele Bellini, Alessio Meneghetti
    On the Griesmer bound for nonlinear codes Emanuele Bellini, Alessio Meneghetti To cite this version: Emanuele Bellini, Alessio Meneghetti. On the Griesmer bound for nonlinear codes. WCC2015 - 9th International Workshop on Coding and Cryptography 2015, Anne Canteaut, Gaëtan Leurent, Maria Naya-Plasencia, Apr 2015, Paris, France. hal-01276224 HAL Id: hal-01276224 https://hal.inria.fr/hal-01276224 Submitted on 19 Feb 2016 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. On the Griesmer bound for nonlinear codes Emanuele Bellini1 and Alessio Meneghetti2 1 Telsy S.p.A., Italy [email protected] 2 University of Trento, Italy [email protected] Abstract. Most bounds on the size of codes hold for any code, whether linear or nonlinear. Notably, the Griesmer bound holds only in the linear case. In this paper we identify code parameters (q; d; k) for which the Griesmer bound holds also in the (systematic) nonlinear case. Moreover, we show that the Griesmer bound does not necessarily hold for a systematic code by showing explicit counterexamples. On the other hand, we are also able to provide some versions of the Griesmer bound holding for all systematic codes.
    [Show full text]
  • Introduction to Coding Theory Ron M
    Cambridge University Press 978-0-521-84504-5 - Introduction to Coding Theory Ron M. Roth Index More information Index adjacency matrix block code, 5 of digraphs, 486 Blokh–Zyablov bound, 393 of graphs, 398 bound Lee, 325 BCH, 253 alphabet, 3 Bhattacharyya, 21, 25, 493 alternant code, 70, 157, 179 Blokh–Zyablov, 393 decoding of, 197, 204 Carlitz–Uchiyama, 179 Lee-metric, 306 Chernoff, 139 list, 280, 328 decoding-radius, 290 designed minimum distance of, 157, Elias, 108 250 Lee-metric, 332 dual code of, 175, 180 Gilbert–Varshamov, 97, 137, 176, 181, Lee-metric, 302 393 list decoding of, 280, 328 asymptotic, 107, 372 over Z, 328 Lee-metric, 320, 330 aperiodic irreducible digraph, 455 Griesmer, 120, 136 aperiodic irreducible matrix, 445 Hamming, see bound, sphere-packing arc (in projective geometry), 361 Hartmann–Tzeng, 265 complete, 363 Johnson, 107, 128, 139, 289 autocorrelation Lee-metric, 330 of Legendre sequences, 80 linear programming, 103, 110, 138 of maximal-length sequences, 87 MDS code length, 338 AWGN channel, 17 MRRW, 110 Plotkin, 37, 127, 131, 139, 294 basis Lee-metric, 326, 330 complementary, 85 Reiger, 122 dual, 85 Roos, 265 see normal, 240 Singleton, Singleton bound BCH bound, 253 sphere-covering, 123 BCH code, 162, 181, 244, 250 sphere-packing, 95, 122, 136 consecutive root sequence of, 163 asymptotic, 107 decoding of, see alternant code, decod- Lee-metric, 318, 330 ing of union, 137 designed minimum distance of, 163, Zyablov, 373, 392, 413, 422, 438, 440 250 burst, 45, 122, 137, 257 excess root of, 251 root of, 163, 250 cap
    [Show full text]
  • Lecture 5 1 Recap
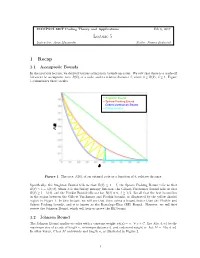
    COMPSCI 690T Coding Theory and Applications Feb 6, 2017 Lecture 5 Instructor: Arya Mazumdar Scribe: Names Redacted 1 Recap 1.1 Asymptotic Bounds In the previous lecture, we derived various asymptotic bounds on codes. We saw that there is a trade-off between the asymptotic rate, R(δ), of a code, and its relative distance δ, where 0 ≤ R(δ); δ ≤ 1. Figure 1 summarizes these results. －Singleton Bound －Sphere Packing Bound －Gilbert-Varshamov Bound －Plotkin Bound ) R( Figure 1: The rate, R(δ), of an optimal code as a function of δ, relative distance. Specifically, the Singleton Bound tells us that R(δ) ≤ 1 − δ, the Sphere Packing Bound tells us that R(δ) ≤ 1 − h(δ=2), where h is the binary entropy function, the Gilbert-Varshamov Bound tells us that R(δ) ≥ 1 − h(δ), and the Plotkin Bound tells us that R(δ) = 0; δ ≥ 1=2. Recall that the best bound lies in the region between the Gilbert-Varshamov and Plotkin bounds, as illustrated by the yellow shaded region in Figure 1. In this lecture, we will see that there exists a bound better than the Plotkin and Sphere Packing bounds, and it is known as the Bassalygo-Elias (BE) Bound. However, we will first review the Johnson Bound, which will help us prove the BE bound. 1.2 Johnson Bound The Johnson Bound applies to codes with a constant weight wt(x) = w; 8 x 2 C. Let A(n; d; w) be the maximum size of a code of length n, minimum distance d, and codeword weight w.
    [Show full text]
  • Some Bounds on the Size of Codes
    Some bounds on the size of codes Emanuele Bellini ([email protected]) Department of Mathematics, University of Trento, Italy. Eleonora Guerrini ([email protected]) LIRMM, UniversitA˜ c de Montpellier 2, France. Massimiliano Sala ([email protected]) Department of Mathematics, University of Trento, Italy. Abstract We present some upper bounds on the size of non-linear codes and their restriction to systematic codes and linear codes. These bounds are independent of other known theoretical bounds, e.g. the Griesmer bound, the Johnson bound or the Plotkin bound, and one of these is actually an improvement of a bound by Litsyn and Laihonen. Our experiments show that in some cases (the majority of cases for some q) our bounds provide the best value, compared to all other theoretical bounds. Keywords: Hamming distance, linear code, systematic code, non-linear code, upper bound. arXiv:1206.6006v2 [cs.IT] 27 Dec 2012 1 Introduction The problem of bounding the size of a code depends heavily on the code family that we are considering. In this paper we are interested in three types of codes: linear codes, systematic codes and non-linear codes. Referring to the subsequent section for rigorous definitions, with linear codes we mean n linear subspaces of (Fq) , while with non-linear codes we mean (following consolidated tradition) codes that are not necessarily linear. In this sense, a linear code is always a non-linear code, while a non-linear code may be a linear code, although it is unlikely. Systematic codes form a less-studied family of codes, whose definition is given in the next section.
    [Show full text]
  • Notes 4: Elementary Bounds on Codes 1 Singleton Bound
    Introduction to Coding Theory CMU: Spring 2010 Notes 4: Elementary bounds on codes January 2010 Lecturer: Venkatesan Guruswami Scribe: Venkatesan Guruswami We now turn to limitations of codes, in the form upper bounds on the rate of codes as a function of their relative distance. We will typically give concrete bounds on the size of codes, and then infer as corollaries the asymptotic statement for code families relating rate and relative distance. All the bounds apply for general codes and they do not take advantage of linearity. However, for the most sophisticated of our bounds, the linear programming bound, which we discuss in the next set of notes, we will present the proof only for linear codes as it is simpler in this case. We recall the two bounds we have already seen. The Gilbert-Varshamov bound asserted the ex- n istence of (linear) q-ary codes of block length n, distance at least d, and size at least q . Volq(n;d−1) Or in asymptotic form, the existence of codes of rate approaching 1 − hq(δ) and relative distance δ. The Hamming or sphere-packing bound gave an upper bound on the size (or rate) of codes, which is our focus in these notes. The Hamming bound says that a q-ary code of block length n n and distance d can have at most q codewords. Or in asymptotic form, a q-ary code Volq(n;b(d−1)=2c) of relative distance δ can have rate at most 1 − hq(δ=2) + o(1). As remarked in our discussion on Shannon's theorem for the binary symmetric channel, if the Hamming bound could be attained, that would imply that we can correct all (as opposed to most) error patterns of weight pn with rate approaching 1 − h(p).
    [Show full text]
  • Comparing Bounds on Binary Error-Correcting Codes
    Comparing bounds on binary error-correcting codes S.L.F.van Alebeek Delft University of Technology Delft University of Technology Faculty of Electrical Engineering, Mathematics and Computer Science Delft Institute of Applied Mathematics Comparing bounds on binary error-correcting codes (Dutch title: Vergelijken van grenzen voor binaire foutverbeterende codes) A thesis submitted to the Delft Institute of Applied Mathematics in partial fulfillment of the requirements for the degree BACHELOR OF SCIENCE in APPLIED MATHEMATICS by Sanne van Alebeek Delft, Nederland Maart, 2017 Copyright © 2017 by Sanne van Alebeek. All rights reserved. BSc THESIS APPLIED MATHEMATICS “Comparing bounds on binary error-correcting codes” (Dutch title: “Vergelijken van grenzen voor binaire foutverbeterende codes”) Sanne van Alebeek Delft University of Technology Supervisor Dr.ir. J.H. Weber Thesis committee Dr. D. C. Gijswijt Drs. E.M. van Elderen Dr. D. Kurowicka March, 2017 Delft PREFACE Delft, March 2017 My first encounter with error-correcting codes was already during high school, when I was working on a school project ("profielwerkstuk"). In particular I was intrigued by the special characteristics of a Hamming code. During my studies I also followed the course "Toegepaste algebra, codes en cryptosystemen", where we dove deeper into this subject. One of the lecturers, Joost de Groot, made the suggestion of bounds on error-correcting codes as a subject for a bachelor thesis, where as a result this report now lies in front of you. I would like to extend my gratitude to my thesis supervisor, Jos Weber, for his patience, guidance and support, and his critical questions and remarks. Also I would like to thank my thesis committee for taking the time to read and critically review my thesis.
    [Show full text]
  • Some Bounds on the Size of Codes
    Noname manuscript No. (will be inserted by the editor) Some bounds on the size of codes Emanuele Bellini · Eleonora Guerrini · Massimiliano Sala Received: date / Accepted: date Abstract We present some upper bounds on the size of non-linear codes and their restriction to systematic codes and linear codes. These bounds are independent of other known theoretical bounds, e.g. the Griesmer bound, the Johnson bound or the Plotkin bound, and one of these is actually an improvement of a bound by Zinoviev, Litsyn and Laihonen. Our experiments show that in some cases (the majority of cases for some q) our bounds provide the best value, compared to all other theoretical bounds. Keywords Hamming distance · linear code · systematic code · non-linear code · upper bound 1 Introduction The problem of bounding the size of a code depends heavily on the code family that we are considering. In this paper we are interested in three types of codes: linear codes, systematic codes and non-linear codes. Referring to the subsequent section for rigorous definitions, with linear codes we mean linear subspaces of n (Fq) , while with non-linear codes we mean (following consolidated tradition) codes that are not necessarily linear. Systematic codes form a less-studied family of codes, whose definition is given in the next section. The size of a systematic code is directly comparable with that of a linear code, since it is a power of the field size. E. Bellini University of Trento E-mail: [email protected] E. Guerrini LIRMM, University of Montpellier 2, France. E-mail: [email protected] M.
    [Show full text]