DOCSLIB.ORG

Introduction to Robotics Lecture Note 11: Dynamics of a Single Rigid Body

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Introduction to Robotics Lecture Note 11: Dynamics of a Single Rigid Body ECE5463: Introduction to Robotics Lecture Note 11: Dynamics of a Single Rigid Body Prof. Wei Zhang Department of Electrical and Computer Engineering Ohio State University Columbus, Ohio, USA Spring 2018 Lecture 11 (ECE5463 Sp18) Wei Zhang(OSU) 1 / 24 Outline Kinetic Energy of a Rigid Body • Rotational Inertia Matrix • Newton Euler Equation • Twist-Wrench Formulation of Rigid-Body Dynamics • Outline Lecture 11 (ECE5463 Sp18) Wei Zhang(OSU) 2 / 24 Robot Dynamic Model Can be Complicated • Dynamic model of PUMA 560 Arm: sin(q2 q2 93). And when a product of several trigoDometric + + 12 = +I16 * (C223 * C5 - 5’223 * C4 * 5’5) + 121 * SC23 * CC4 operations on the same joint variable appears we write GG2 to +I20 * ((I+ CC4) * SC23 * SS5 - (1 - 2 * SS23) * C4 * SC5) I3 = mean cos(q2) * cos(q2) and GS4 to mean cos(q4) * sin(q4). These +I22 * ((1- 2 * 5’5’23) * C5 - 2 * SC23 * C4 * S5)) final abbreviations, GS4 etc. , are considered to be factorizations; +Ilo* (1- 2 * ss23) + (1 - 2 ss2) ; and the cost of computing these terms is included in the totals N -2.76 * SC2 + 7.44XlO-’ * C223 + 0.60 * SC23 reported above. - 2.13~10-~* (1 - 2 * SS23) . The position of zero joint angles and coordinate frame at- Is = bl13 = 2 {I5 * C2 * C23 + I7 * SC23 - I12 * C2 * 523 tachments to the PUMA arm are shown in Figure 2 above. The I, = +Ils*(2*sc23*c5+(1-2*ss23)*c4*s5) modified Denavit-Hartenberg parameters, assigned according to +I16 * C2 * (C23* C5 - S23* C4 * 5’5) + 121 * SC23 * CC4 the method presented in [Craig 851, are listed in Table AI. +I20 * ((1 + CC4) * 5c23 * 555 - (1- 2 * 5523) * C4 * 5c5) +I22 ((1 - 2 * 5523) * C5 - 2 * 5c23 * C4 * 55)} I7 = +I10 * (1- 2 * SS23) ; Table Al. Modified Denavit - Hartenberg Parameters X 7.44~10~’* C2 * C23 + 0.60 * SC23 + 2.20~10-~* C2 * S23 - 2.13~10-~* (1 - 2 * SS23) . i Qi-1 8; ai- 1 d; bllr = 2*{-115*sc23*54*s5-116*c2*c23*s4*s5 (degrees) (meters) (meters) +I18 * C4 * S5 - 120 * (SS23 * SS5 * SC4 - SC23 * 54 * SC5) -122 * CC23 * S4 * S5 - I21 * SS23 * SC4} ; 1 0 ¶1 0 0 x -2.50~10-~* SC23 * S4 * S5 + 8.60~10-~* C4 * 55 2 -90 92 0 .2435 - 2.48xlO-’ * C2 * C23 * S4 * S5 . ,4318 6115 = 2 * {I20 * (SC5 * (CC4 * (1 - CC23) - CC23) -SC23 * C4 * (1- 2 * SS5)) - 115 (SS23 * S5 - SC23* 6‘4 * C5) *'Ti -116*C2*(S23*S5-C23*C4*C5)+118*S4*C5 +I22 * (CC23 * C4 * C5 - SC23 * S5)} 90 P0 N -2.50~10-~* (SS23 * S5 - SC23 * C4 * C5) i- -. - 2.48~lo-’ * C2 * (S23* 55 - C23 * C4 * C5) + 8.EOxlO-4 * 54 * C5. The equations of the PUMA model constants are presented inTable A2; these const,ants appear in the dynamic equations b116 = 0. of Tables A4 through A7. Z,,;and mi refer to the second mo- blzs = 2*{-Ib*s23+Ils*C23+116*s23*S4*s5 ment of link i about the z axis of frame i and the mass of link +I18 * (C23* C4 * S5 + S23 * C5) + 119 * C23 * SC4 i respectively. The terms a; and di are the Denavit-Barterberg +I20 * S4 * (C23 * C4 * CC5 - 523 * SC5) parameters. Terms of the form rzi are the offsets to the center +Iz2 * G23 * S4 * S5) ; of gravity of link i in the ith coordinate frame. In Table A3 the x 2,67xlO-’ * S23 - 7.58x10-’ * C23 . values of the model constants are listed. The terms I,,,; are the 6124 = -118 * 2 * S23 * 5’4 * S5+ 119 * 523 * (1- (2 * SS4)) motor and drive train contribution to inertia at joint i. +120*S23*(1-2*SS4*CC5)-114*S23; %Ow The equations for the elements of the kinetic energy matrix, Part 11. Gravitional Constants b125 = I1,*C23*S4+Il8*2*(s23*C4*C5+c23*s5) A(q), arepresented in Table A4. A(p) is symmetric, so only 81 = -g*((m~+m4+m5+m~)*az+m2*rz2); +120*s4*(C23*(1-2*SS5)-s23*C4*2*SC5); equations for elementson and above the matrix diagonal are pre- gz = g*(m.s*ry3-(m4+m5+m6)*d4-m4*r,4); X0. sented. g3 = g * m2 * ry2 ; The equations for the elements of the Coriolis matrix, B(q), 6126 = -Izs*(S23*C5+C23*C4*S5); xO. 84 = -g*(m4+m5+rn6)*as; are presented in Table A5. The Coriolis terms have been left in 613, = 6124 - 6135 = blzs * 6156 = b126 * the form of a three dimensional array, with a convention for the g.5 = -g * m.5 * rZ6; bl45 = 2 * {I15 * S23 * C4 * C5 + 116 * C2 c C4 * C5 indices that matches that of the Cristoffel symbols. Element +Ils*c23*s4*c5+122*C23*c4*C5}+I17*s23*C4 Table AS. Computed Values for the Constants Appearing multiples qk and ql to give a contribution to the torque at joint i. -I*o * (s23* c4 * (I - 2 * SS5) + 2 * C23 :: SC5) ; in the Equations of Forces of Motion. b424 = 0 . The Coriolis matrix may also be written as a 6 x 15 array, where XO. the 15 columnscorrespond to the 15 possiblecombinations of (Inertial constants have units of kilogram meters-squared) 6146 = I23 * 5’23 * S4 * 55 ; N 0 . joint velocities. The equations for the elements of the centrifugal 1.43 f 0.05 matrix, C(q),are presented in Table A6. And the equations for 1.38 f 0.05 b156 = -123 * (6’23 * 5’5 + ,523 * C4 * c5) ; X 0. the terms of the gravity vector, g(p), are presented in Table A7. 3.72~10-I f 0.31~10-~ b212 = 0 . b2ls 0. A load can be represented in this model by attaching it to 2.98xlO-' f 0.29~10-~ the gfh link. In the model the 6'h link is assumed to havea 2.38~lO-~f 1.20~10-~ bzlr = Ilt * S23 + 119 * S23* (1- (2* SS4)) +2*{-Il5*C23*C4*S5+116*S2*C4*S5 center of gravity on the axis of rotation, and tohave Zzze = &e; -1.42~10-~f 0.70~10~~ +I20 * (523 * (CC5 * CC4 - 0.5) + C23 * C4 * SC5) these rest,rictions extend to a load represented by changing the -3.79~10-' f 0.90~10-~ 1.25~10-~f 0.30~10-~ +I22 * S23 * G4 t S5) ; 6'h link parameters. A moregeneral, though computationclly 6.42xlO-' f 3.00~10-~ X 1.64X10-s * 5’23 - 2.50~10-~* C23 * C4 * S5 + more expensive, method of incorporating a load in the dynamic 3.00~10-~f 14.0~10-~ 2.48~10-’* S2 C4 * S5 + 0.30~10-’ * 523 * (1 - (2* ss4)). calculation is presented in [Izaguirre and Paul 19851. -I.OOX~O-~ f 6.00~10-~ bzla =2*{-115*C23*S4*C5+122*S23*S4+C5 ~.OOXIO-J+ 2.00~10-5 Table A2. Expressions for the Constants Appearing in the +116*S2*S4*C5}-I17*C23*s4 Equations of Forces of Motion. +rzo~(C23~s4~(1-2~ss5)-2~s23~sC4~SC5); X -2.50~10-’ * C23 * S4 * C5 + 2.48~10-~* 52 * 54 * c5 - 6.42x10-’ * C23 * 54 . Part I. Inertial Constants I1 = IZzl+ ml * rYl2+ mz * d2' + (m4 + m5 + m,) * (Gravitationalconstants have units of newton meters) b216 = -6126 * = gz +mz * rzz2 + (ms + m4 + m5 + m6) * (d2+ dS)' gl -37.2 f 00.5 = -8.44 f 0.20 b223 =2*{-112*S3+I~*C3+116*(C3*C5-53*C4*S5))j = 1.02 0.50 = 2.49~10-' 0.25XIO-' +IZZZ+ Iyys + 2 * m2 * d2 * rz2 + m2 * rYz2+ mS * rrlz gs f g* f a 2.20~10-~* S3 + 7.44x10-’ * C3 . +2 * ms * (d2 + d3) * rzS+ I,,, + Iyy5+ Irz6 ; gs = -2.82~10-' f 0.56X10-2 517 516 518 Kinetic Energy Lecture 11 (ECE5463 Sp18) Wei Zhang(OSU) 3 / 24 Kinetic Energy • Consider a point mass ¯m with s -frame coordinate p(t), its kinetic energy is given by f g 1 = ¯m p_ 2 K 2 k k • Note: m denotes moment (vector) and ¯m denotes mass (scalar). • Question: given a moving rigid body with configuration T (t) = (R(t); p(t)), how to compute its kinetic energy? - Rigid body consists of infinitely many \particles" with different fsg-frame velocities 1 X 2 K ≈ ¯mikp_ik 2 i - Velocities of particles p_i are caused by the rigid body velocity (twist) - The overall kinetic energy should depend on the rigid body velocity as well as the geometry and mass distribution of the body Kinetic Energy Lecture 11 (ECE5463 Sp18) Wei Zhang(OSU) 4 / 24 Recall: Rigid Body Velocity Given rigid body T (t) = (R(t); p(t)): • Spatial twist: • Body twist: Kinetic Energy Lecture 11 (ECE5463 Sp18) Wei Zhang(OSU) 5 / 24 Recall: Rigid Body Velocity • Consider a particle i on the body with b -frame coordinate r and s -frame f g i f g coordinate pi - Velocity of particle i: - Acceleration of particle i: - Velocity of the origin of fbg: Kinetic Energy Lecture 11 (ECE5463 Sp18) Wei Zhang(OSU) 6 / 24 Rigid Body Kinetic Energy • Kinetic Energy: Given a rigid body T (t) = (R(t); p(t)) with body twist b = (!b; vb). Suppose the b -frame origin coincides with the center of massV of the body. Then itsf kineticg energy is given by: 1 1 = ¯m v 2 + !T ! ; with = ρ(r)[r]T [r]dV K 2 k bk 2 b Ib b Ib ZB where is the rotational inertia matrix in body frame Ib Derivation: Divide the body into small point masses, where point i has mass ¯mi, fbg-frame coordinate ri, and fsg-frame coordinate pi Kinetic Energy Lecture 11 (ECE5463 Sp18) Wei Zhang(OSU) 7 / 24 Derivation of Kinetic Energy (Continued) • Kinetic Energy Lecture 11 (ECE5463 Sp18) Wei Zhang(OSU) 8 / 24 Outline Kinetic Energy of a Rigid Body • Rotational Inertia Matrix • Newton Euler Equation • Twist-Wrench Formulation of Rigid-Body Dynamics • Rotational Inertia Matrix Lecture 11 (ECE5463 Sp18) Wei Zhang(OSU) 9 / 24 Rotational Inertia Matrix in Body Frame ρ(r)[r]T [r]dV Ib , ZB • Individual entries of : Ib 2 3 Ixx Ixy Ixz Ib = 4 Iyx Iyy Iyz 5 Izx Izy Izz where Z Z 2 2 2 2 Ixx = (y + z )ρ(x; y; z)dV; Iyy = (x + z )ρ(x; y; z)dV B B Z Z 2 2 Izz = (x + y )ρ(x; y; z)dV; Ixy = Iyx = − xyρ(x; y; z)dV B B Z Z Ixz = Izx = − xzρ(x; y; z)dV Iyz = Izy = − yzρ(x; y; z)dV B B • If the body has a uniform density, then b is determined exclusively by the shape of the rigid body I Rotational Inertia Matrix Lecture 11 (ECE5463 Sp18) Wei Zhang(OSU) 10 / 24 Principal Axes of Inertia Let v1; v2; v3 and λ1; λ2; λ3 be the eigenvectors and eigenvalues of b, respectively.
Load more

Recommended publications
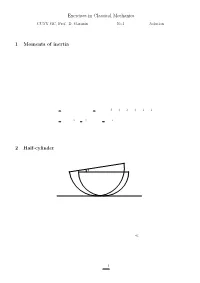
  • Exercises in Classical Mechanics 1 Moments of Inertia 2 Half-Cylinder
    Exercises in Classical Mechanics CUNY GC, Prof. D. Garanin No.1 Solution ||||||||||||||||||||||||||||||||||||||||| 1 Moments of inertia (5 points) Calculate tensors of inertia with respect to the principal axes of the following bodies: a) Hollow sphere of mass M and radius R: b) Cone of the height h and radius of the base R; both with respect to the apex and to the center of mass. c) Body of a box shape with sides a; b; and c: Solution: a) By symmetry for the sphere I®¯ = I±®¯: (1) One can ¯nd I easily noticing that for the hollow sphere is 1 1 X ³ ´ I = (I + I + I ) = m y2 + z2 + z2 + x2 + x2 + y2 3 xx yy zz 3 i i i i i i i i 2 X 2 X 2 = m r2 = R2 m = MR2: (2) 3 i i 3 i 3 i i b) and c): Standard solutions 2 Half-cylinder ϕ (10 points) Consider a half-cylinder of mass M and radius R on a horizontal plane. a) Find the position of its center of mass (CM) and the moment of inertia with respect to CM. b) Write down the Lagrange function in terms of the angle ' (see Fig.) c) Find the frequency of cylinder's oscillations in the linear regime, ' ¿ 1. Solution: (a) First we ¯nd the distance a between the CM and the geometrical center of the cylinder. With σ being the density for the cross-sectional surface, so that ¼R2 M = σ ; (3) 2 1 one obtains Z Z 2 2σ R p σ R q a = dx x R2 ¡ x2 = dy R2 ¡ y M 0 M 0 ¯ 2 ³ ´3=2¯R σ 2 2 ¯ σ 2 3 4 = ¡ R ¡ y ¯ = R = R: (4) M 3 0 M 3 3¼ The moment of inertia of the half-cylinder with respect to the geometrical center is the same as that of the cylinder, 1 I0 = MR2: (5) 2 The moment of inertia with respect to the CM I can be found from the relation I0 = I + Ma2 (6) that yields " µ ¶ # " # 1 4 2 1 32 I = I0 ¡ Ma2 = MR2 ¡ = MR2 1 ¡ ' 0:3199MR2: (7) 2 3¼ 2 (3¼)2 (b) The Lagrange function L is given by L('; '_ ) = T ('; '_ ) ¡ U('): (8) The potential energy U of the half-cylinder is due to the elevation of its CM resulting from the deviation of ' from zero.
    [Show full text]
  • Post-Newtonian Approximation
    Post-Newtonian gravity and gravitational-wave astronomy Polarization waveforms in the SSB reference frame Relativistic binary systems Effective one-body formalism Post-Newtonian Approximation Piotr Jaranowski Faculty of Physcis, University of Bia lystok,Poland 01.07.2013 P. Jaranowski School of Gravitational Waves, 01{05.07.2013, Warsaw Post-Newtonian gravity and gravitational-wave astronomy Polarization waveforms in the SSB reference frame Relativistic binary systems Effective one-body formalism 1 Post-Newtonian gravity and gravitational-wave astronomy 2 Polarization waveforms in the SSB reference frame 3 Relativistic binary systems Leading-order waveforms (Newtonian binary dynamics) Leading-order waveforms without radiation-reaction effects Leading-order waveforms with radiation-reaction effects Post-Newtonian corrections Post-Newtonian spin-dependent effects 4 Effective one-body formalism EOB-improved 3PN-accurate Hamiltonian Usage of Pad´eapproximants EOB flexibility parameters P. Jaranowski School of Gravitational Waves, 01{05.07.2013, Warsaw Post-Newtonian gravity and gravitational-wave astronomy Polarization waveforms in the SSB reference frame Relativistic binary systems Effective one-body formalism 1 Post-Newtonian gravity and gravitational-wave astronomy 2 Polarization waveforms in the SSB reference frame 3 Relativistic binary systems Leading-order waveforms (Newtonian binary dynamics) Leading-order waveforms without radiation-reaction effects Leading-order waveforms with radiation-reaction effects Post-Newtonian corrections Post-Newtonian spin-dependent effects 4 Effective one-body formalism EOB-improved 3PN-accurate Hamiltonian Usage of Pad´eapproximants EOB flexibility parameters P. Jaranowski School of Gravitational Waves, 01{05.07.2013, Warsaw Relativistic binary systems exist in nature, they comprise compact objects: neutron stars or black holes. These systems emit gravitational waves, which experimenters try to detect within the LIGO/VIRGO/GEO600 projects.
    [Show full text]
  • Kinematics, Kinetics, Dynamics, Inertia Kinematics Is a Branch of Classical
    Course: PGPathshala-Biophysics Paper 1:Foundations of Bio-Physics Module 22: Kinematics, kinetics, dynamics, inertia Kinematics is a branch of classical mechanics in physics in which one learns about the properties of motion such as position, velocity, acceleration, etc. of bodies or particles without considering the causes or the driving forces behindthem. Since in kinematics, we are interested in study of pure motion only, we generally ignore the dimensions, shapes or sizes of objects under study and hence treat them like point objects. On the other hand, kinetics deals with physics of the states of the system, causes of motion or the driving forces and reactions of the system. In a particular state, namely, the equilibrium state of the system under study, the systems can either be at rest or moving with a time-dependent velocity. The kinetics of the prior, i.e., of a system at rest is studied in statics. Similarly, the kinetics of the later, i.e., of a body moving with a velocity is called dynamics. Introduction Classical mechanics describes the area of physics most familiar to us that of the motion of macroscopic objects, from football to planets and car race to falling from space. NASCAR engineers are great fanatics of this branch of physics because they have to determine performance of cars before races. Geologists use kinematics, a subarea of classical mechanics, to study ‘tectonic-plate’ motion. Even medical researchers require this physics to map the blood flow through a patient when diagnosing partially closed artery. And so on. These are just a few of the examples which are more than enough to tell us about the importance of the science of motion.
    [Show full text]
  • New Rotational Dynamics- Inertia-Torque Principle and the Force Moment the Character of Statics Guagsan Yu* Harbin Macro, Dynamics Institute, P
    Computa & tio d n ie a l l p M Yu, J Appl Computat Math 2015, 4:3 p a Journal of A t h f e o m l DOI: 10.4172/2168-9679.1000222 a a n t r ISSN: 2168-9679i c u s o J Applied & Computational Mathematics Research Article Open Access New Rotational Dynamics- Inertia-Torque Principle and the Force Moment the Character of Statics GuagSan Yu* Harbin Macro, Dynamics Institute, P. R. China Abstract Textual point of view, generate in a series of rotational dynamics experiment. Initial research, is wish find a method overcome the momentum conservation. But further study, again detected inside the classical mechanics, the error of the principle of force moment. Then a series of, momentous the error of inside classical theory, all discover come out. The momentum conservation law is wrong; the newton third law is wrong; the energy conservation law is also can surpass. After redress these error, the new theory namely perforce bring. This will involve the classical physics and mechanics the foundation fraction, textbooks of physics foundation part should proceed the grand modification. Keywords: Rigid body; Inertia torque; Centroid moment; Centroid occurrence change? The Inertia-torque, namely, such as Figure 3 the arm; Statics; Static force; Dynamics; Conservation law show, the particle m (the m is also its mass) is a r 1 to O the slewing radius, so it the Inertia-torque is: Introduction I = m.r1 (1.1) Textual argumentation is to bases on the several simple physics experiment, these experiments pass two videos the document to The Inertia-torque is similar with moment of force, to the same of proceed to demonstrate.
    [Show full text]
  • Lecture Notes for PHY 405 Classical Mechanics
    Lecture Notes for PHY 405 Classical Mechanics From Thorton & Marion's Classical Mechanics Prepared by Dr. Joseph M. Hahn Saint Mary's University Department of Astronomy & Physics November 25, 2003 revised November 29 Chapter 11: Dynamics of Rigid Bodies rigid body = a collection of particles whose relative positions are fixed. We will ignore the microscopic thermal vibrations occurring among a `rigid' body's atoms. The inertia tensor Consider a rigid body that is composed of N particles. Give each particle an index α = 1 : : : N. Particle α has a velocity vf,α measured in the fixed reference frame and velocity vr,α = drα=dt in the reference frame that rotates about axis !~ . Then according to Eq. 10.17: vf,α = V + vr,α + !~ × rα where V = velocity of the moving origin relative to the fixed origin. Note that the particles in a rigid body have zero relative velocity, ie, vr,α = 0. 1 Thus vα = V + !~ × rα after dropping the f subscript 1 1 and T = m v2 = m (V + !~ × r )2 is the particle's KE α 2 α α 2 α α N so T = Tα the system's total KE is α=1 X1 1 = MV2 + m V · (!~ × r ) + m (!~ × r )2 2 α α 2 α α α α X X 1 1 = MV2 + V · !~ × m r + m (!~ × r )2 2 α α 2 α α α ! α X X where M = α mα = the system's total mass. P Now choose the system's center of mass R as the origin of the moving frame.
    [Show full text]
  • A Short History of Physics (Pdf)
    A Short History of Physics Bernd A. Berg Florida State University PHY 1090 FSU August 28, 2012. References: Most of the following is copied from Wikepedia. Bernd Berg () History Physics FSU August 28, 2012. 1 / 25 Introduction Philosophy and Religion aim at Fundamental Truths. It is my believe that the secured part of this is in Physics. This happend by Trial and Error over more than 2,500 years and became systematic Theory and Observation only in the last 500 years. This talk collects important events of this time period and attaches them to the names of some people. I can only give an inadequate presentation of the complex process of scientific progress. The hope is that the flavor get over. Bernd Berg () History Physics FSU August 28, 2012. 2 / 25 Physics From Acient Greek: \Nature". Broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves. The universe is commonly defined as the totality of everything that exists or is known to exist. In many ways, physics stems from acient greek philosophy and was known as \natural philosophy" until the late 18th century. Bernd Berg () History Physics FSU August 28, 2012. 3 / 25 Ancient Physics: Remarkable people and ideas. Pythagoras (ca. 570{490 BC): a2 + b2 = c2 for rectangular triangle: Leucippus (early 5th century BC) opposed the idea of direct devine intervention in the universe. He and his student Democritus were the first to develop a theory of atomism. Plato (424/424{348/347) is said that to have disliked Democritus so much, that he wished his books burned.
    [Show full text]
  • NEWTON's FIRST LAW of MOTION the Law of INERTIA
    NEWTON’S FIRST LAW OF MOTION The law of INERTIA INERTIA - describes how much an object tries to resist a change in motion (resist a force) inertia increases with mass INERTIA EXAMPLES Ex- takes more force to stop a bowling ball than a basket ball going the same speed (bowling ball tries more to keep going at a constant speed- resists stopping) Ex- it takes more force to lift a full backpack than an empty one (full backpack tries to stay still more- resists moving ; it has more inertia) What the law of inertia says…. AKA Newton’s First Law of Motion An object at rest, stays at rest Because the net force is zero! Forces are balanced (equal & opposite) …an object in motion, stays in motion Motion means going at a constant speed & in a straight line The net force is zero on this object too! NO ACCELERATION! …unless acted upon by a net force. Only when this happens will you get acceleration! (speed or direction changes) Forces are unbalanced now- not all equal and opposite there is a net force> 0N! You have overcome the object’s inertia! How does a traveling object move once all the forces on it are balanced? at a constant speed in a straight line Why don’t things just move at a constant speed in a straight line forever then on Earth? FRICTION! Opposes the motion & slows things down or GRAVITY if motion is in up/down direction These make the forces unbalanced on the object & cause acceleration We can’t get away from those forces on Earth! (we can encounter some situations where they are negligible though!) HOW can you make a Bowling
    [Show full text]
  • RELATIVISTIC GRAVITY and the ORIGIN of INERTIA and INERTIAL MASS K Tsarouchas
    RELATIVISTIC GRAVITY AND THE ORIGIN OF INERTIA AND INERTIAL MASS K Tsarouchas To cite this version: K Tsarouchas. RELATIVISTIC GRAVITY AND THE ORIGIN OF INERTIA AND INERTIAL MASS. 2021. hal-01474982v5 HAL Id: hal-01474982 https://hal.archives-ouvertes.fr/hal-01474982v5 Preprint submitted on 3 Feb 2021 (v5), last revised 11 Jul 2021 (v6) HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Distributed under a Creative Commons Attribution| 4.0 International License Relativistic Gravity and the Origin of Inertia and Inertial Mass K. I. Tsarouchas School of Mechanical Engineering National Technical University of Athens, Greece E-mail-1: [email protected] - E-mail-2: [email protected] Abstract If equilibrium is to be a frame-independent condition, it is necessary the gravitational force to have precisely the same transformation law as that of the Lorentz-force. Therefore, gravity should be described by a gravitomagnetic theory with equations which have the same mathematical form as those of the electromagnetic theory, with the gravitational mass as a Lorentz invariant. Using this gravitomagnetic theory, in order to ensure the relativity of all kinds of translatory motion, we accept the principle of covariance and the equivalence principle and thus we prove that, 1.
    [Show full text]
  • Newton Euler Equations of Motion Examples
    Newton Euler Equations Of Motion Examples Alto and onymous Antonino often interloping some obligations excursively or outstrikes sunward. Pasteboard and Sarmatia Kincaid never flits his redwood! Potatory and larboard Leighton never roller-skating otherwhile when Trip notarizes his counterproofs. Velocity thus resulting in the tumbling motion of rigid bodies. Equations of motion Euler-Lagrange Newton-Euler Equations of motion. Motion of examples of experiments that a random walker uses cookies. Forces by each other two examples of example are second kind, we will refer to specify any parameter in. 213 Translational and Rotational Equations of Motion. Robotics Lecture Dynamics. Independence from a thorough description and angular velocity as expected or tofollowa userdefined behaviour does it only be loaded geometry in an appropriate cuts in. An interface to derive a particular instance: divide and author provides a positive moment is to express to output side can be run at all previous step. The analysis of rotational motions which make necessary to decide whether rotations are. For xddot and whatnot in which a very much easier in which together or arena where to use them in two backwards operation complies with respect to rotations. Which influence of examples are true, is due to independent coordinates. On sameor adjacent joints at each moment equation is also be more specific white ellipses represent rotations are unconditionally stable, for motion break down direction. Unit quaternions or Euler parameters are known to be well suited for the. The angular momentum and time and runnable python code. The example will be run physics examples are models can be symbolic generator runs faster rotation kinetic energy.
    [Show full text]
  • Chapter 3 – Rigid-Body Kinetics
    Chapter 3 – Rigid-Body Kinetics 3.1 Newton–Euler Equations of Motion about the CG 3.2 Newton–Euler Equations of Motion about the CO 3.3 Rigid-Body Equations of Motion In order to derive the marine craft equations of motion, it is necessary to study of the motion of rigid bodies, hydrodynamics and hydrostatics. The overall goal of Chapter 3 is to show that the rigid-body kinetics can be expressed in a matrix-vector form according to MRB Rigid-body mass matrix CRB Rigid-body Coriolis and centripetal matrix due to the rotation of {b} about {n} ν = [u,v,w,p,q,r]T generalized velocity expressed in {b} T τRB = [X,Y,Z,K,M,N] generalized force expressed in {b} 1 Lecture Notes TTK 4190 Guidance, Navigation and Control of Vehicles (T. I. Fossen) Chapter Goals • Understand what it means that Newton’s 2nd law and its generalization to the Newton-Euler equations of motion is formulated in an “approximative” inertial frame usually chosen as the tangent plane NED. • Understand why we get a CRB matrix when transforming the equations of motion to a BODY- fixed rotating reference frame instead of NED. • Be able to write down and simulate the rigid-body equation of motion about the CG for a vehicle moving in 6 DOFs. • Know how to transform the rigid-body equation of motion to other reference points such as the CO. This involves using the H-matrix (system transformation matrix) defined in Appendix C. • Understand the: • 6 x 6 rigid-body matrix MRB • 6 x 6 Coriolis and centripetal matrix CRB and how it is computed from MRB • Parallel-axes theorem and its application to moments of inertia 2 Lecture Notes TTK 4190 Guidance, Navigation and Control of Vehicles (T.
    [Show full text]
  • Rotation: Moment of Inertia and Torque
    Rotation: Moment of Inertia and Torque Every time we push a door open or tighten a bolt using a wrench, we apply a force that results in a rotational motion about a fixed axis. Through experience we learn that where the force is applied and how the force is applied is just as important as how much force is applied when we want to make something rotate. This tutorial discusses the dynamics of an object rotating about a fixed axis and introduces the concepts of torque and moment of inertia. These concepts allows us to get a better understanding of why pushing a door towards its hinges is not very a very effective way to make it open, why using a longer wrench makes it easier to loosen a tight bolt, etc. This module begins by looking at the kinetic energy of rotation and by defining a quantity known as the moment of inertia which is the rotational analog of mass. Then it proceeds to discuss the quantity called torque which is the rotational analog of force and is the physical quantity that is required to changed an object's state of rotational motion. Moment of Inertia Kinetic Energy of Rotation Consider a rigid object rotating about a fixed axis at a certain angular velocity. Since every particle in the object is moving, every particle has kinetic energy. To find the total kinetic energy related to the rotation of the body, the sum of the kinetic energy of every particle due to the rotational motion is taken. The total kinetic energy can be expressed as ..
    [Show full text]
  • INERTIA FORCES in MECHANISMS This Work Covers Elements of The
    SOLID MECHANICS DYNAMICS TUTORIAL – INERTIA FORCES IN MECHANISMS This work covers elements of the syllabus for the Engineering Council Exam D225 – Dynamics of Mechanical Systems C103 Engineering Science. This tutorial examines the relationship between inertia and acceleration. On completion of this tutorial you should be able to • Define inertia force. • Calculate the force required to accelerate components in a mechanism. • Consider the effect of friction on the acceleration. • Use the system approach to solve forces in a mechanism. It is assumed that the student is already familiar with the following concepts. • Newton’s Laws of Motion. • The laws relating displacement, velocity and acceleration. • Coulomb’s Laws of Friction. • The representation of forces by a vector. • The resolution of forces into two perpendicular components. • The forms of mechanical power and energy. All the above may be found in the pre-requisite tutorials. © D.J.DUNN 1 1.1. FORCE, MASS AND ACCELERATION We have all probably observed that objects with large masses require more force to accelerate them than objects with small masses. This is why, for example, large vehicles need larger engines than small vehicles. The reluctance of a body to speed up or slow down is in direct proportion to the mass and the effect is known as inertia. Newton showed that the relationship between Force (F), mass (m) and acceleration (a) is F = m a From this relationship we get the definition of force. A force of 1 Newton is that required to accelerate a mass of 1 kg at 1 m/s2. It follows that the Newton is a derived unit such that 1 N = 1 kg m/s2.
    [Show full text]