Prepared by Dr.P.Sumathi COLOR MODELS
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Color Models
Color Models Jian Huang CS456 Main Color Spaces • CIE XYZ, xyY • RGB, CMYK • HSV (Munsell, HSL, IHS) • Lab, UVW, YUV, YCrCb, Luv, Differences in Color Spaces • What is the use? For display, editing, computation, compression, …? • Several key (very often conflicting) features may be sought after: – Additive (RGB) or subtractive (CMYK) – Separation of luminance and chromaticity – Equal distance between colors are equally perceivable CIE Standard • CIE: International Commission on Illumination (Comission Internationale de l’Eclairage). • Human perception based standard (1931), established with color matching experiment • Standard observer: a composite of a group of 15 to 20 people CIE Experiment CIE Experiment Result • Three pure light source: R = 700 nm, G = 546 nm, B = 436 nm. CIE Color Space • 3 hypothetical light sources, X, Y, and Z, which yield positive matching curves • Y: roughly corresponds to luminous efficiency characteristic of human eye CIE Color Space CIE xyY Space • Irregular 3D volume shape is difficult to understand • Chromaticity diagram (the same color of the varying intensity, Y, should all end up at the same point) Color Gamut • The range of color representation of a display device RGB (monitors) • The de facto standard The RGB Cube • RGB color space is perceptually non-linear • RGB space is a subset of the colors human can perceive • Con: what is ‘bloody red’ in RGB? CMY(K): printing • Cyan, Magenta, Yellow (Black) – CMY(K) • A subtractive color model dye color absorbs reflects cyan red blue and green magenta green blue and red yellow blue red and green black all none RGB and CMY • Converting between RGB and CMY RGB and CMY HSV • This color model is based on polar coordinates, not Cartesian coordinates. -

Chapter 6 : Color Image Processing
Chapter 6 : Color Image Processing CCU, Taiwan Wen-Nung Lie Color Fundamentals Spectrum that covers visible colors : 400 ~ 700 nm Three basic quantities Radiance : energy that flows from the light source (measured in Watts) Luminance : a measure of energy an observer perceives from a light source (in lumens) Brightness : a subjective descriptor difficult to measure CCU, Taiwan Wen-Nung Lie 6-1 About human eyes Primary colors for standardization blue : 435.8 nm, green : 546.1 nm, red : 700 nm Not all visible colors can be produced by mixing these three primaries in various intensity proportions Cones in human eyes are divided into three sensing categories 65% are sensitive to red light, 33% sensitive to green light, 2% sensitive to blue (but most sensitive) The R, G, and B colors perceived by CCU, Taiwan human eyes cover a range of spectrum Wen-Nung Lie 6-2 Primary and secondary colors of light and pigments Secondary colors of light magenta (R+B), cyan (G+B), yellow (R+G) R+G+B=white Primary colors of pigments magenta, cyan, and yellow M+C+Y=black CCU, Taiwan Wen-Nung Lie 6-3 Chromaticity Hue + saturation = chromaticity hue : an attribute associated with the dominant wavelength or dominant colors perceived by an observer saturation : relative purity or the amount of white light mixed with a hue (the degree of saturation is inversely proportional to the amount of added white light) Color = brightness + chromaticity Tristimulus values (the amount of R, G, and B needed to form any particular color : X, Y, Z trichromatic -

Pale Intrusions Into Blue: the Development of a Color Hannah Rose Mendoza
Florida State University Libraries Electronic Theses, Treatises and Dissertations The Graduate School 2004 Pale Intrusions into Blue: The Development of a Color Hannah Rose Mendoza Follow this and additional works at the FSU Digital Library. For more information, please contact [email protected] THE FLORIDA STATE UNIVERSITY SCHOOL OF VISUAL ARTS AND DANCE PALE INTRUSIONS INTO BLUE: THE DEVELOPMENT OF A COLOR By HANNAH ROSE MENDOZA A Thesis submitted to the Department of Interior Design in partial fulfillment of the requirements for the degree of Master of Fine Arts Degree Awarded: Fall Semester, 2004 The members of the Committee approve the thesis of Hannah Rose Mendoza defended on October 21, 2004. _________________________ Lisa Waxman Professor Directing Thesis _________________________ Peter Munton Committee Member _________________________ Ricardo Navarro Committee Member Approved: ______________________________________ Eric Wiedegreen, Chair, Department of Interior Design ______________________________________ Sally Mcrorie, Dean, School of Visual Arts & Dance The Office of Graduate Studies has verified and approved the above named committee members. ii To Pepe, te amo y gracias. iii ACKNOWLEDGMENTS I want to express my gratitude to Lisa Waxman for her unflagging enthusiasm and sharp attention to detail. I also wish to thank the other members of my committee, Peter Munton and Rick Navarro for taking the time to read my thesis and offer a very helpful critique. I want to acknowledge the support received from my Mom and Dad, whose faith in me helped me get through this. Finally, I want to thank my son Jack, who despite being born as my thesis was nearing completion, saw fit to spit up on the manuscript only once. -
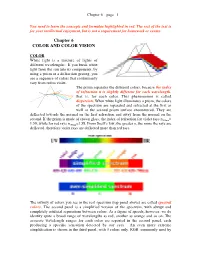
Chapter 6 COLOR and COLOR VISION
Chapter 6 – page 1 You need to learn the concepts and formulae highlighted in red. The rest of the text is for your intellectual enjoyment, but is not a requirement for homework or exams. Chapter 6 COLOR AND COLOR VISION COLOR White light is a mixture of lights of different wavelengths. If you break white light from the sun into its components, by using a prism or a diffraction grating, you see a sequence of colors that continuously vary from red to violet. The prism separates the different colors, because the index of refraction n is slightly different for each wavelength, that is, for each color. This phenomenon is called dispersion. When white light illuminates a prism, the colors of the spectrum are separated and refracted at the first as well as the second prism surface encountered. They are deflected towards the normal on the first refraction and away from the normal on the second. If the prism is made of crown glass, the index of refraction for violet rays n400nm= 1.59, while for red rays n700nm=1.58. From Snell’s law, the greater n, the more the rays are deflected, therefore violet rays are deflected more than red rays. The infinity of colors you see in the real spectrum (top panel above) are called spectral colors. The second panel is a simplified version of the spectrum, with abrupt and completely artificial separations between colors. As a figure of speech, however, we do identify quite a broad range of wavelengths as red, another as orange and so on. -

Computer Graphicsgraphics -- Weekweek 1212
ComputerComputer GraphicsGraphics -- WeekWeek 1212 Bengt-Olaf Schneider IBM T.J. Watson Research Center Questions about Last Week ? Computer Graphics – Week 12 © Bengt-Olaf Schneider, 1999 Overview of Week 12 Graphics Hardware Output devices (CRT and LCD) Graphics architectures Performance modeling Color Color theory Color gamuts Gamut matching Color spaces (next week) Computer Graphics – Week 12 © Bengt-Olaf Schneider, 1999 Graphics Hardware: Overview Display technologies Graphics architecture fundamentals Many of the general techniques discussed earlier in the semester were developed with hardware in mind Close similarity between software and hardware architectures Computer Graphics – Week 12 © Bengt-Olaf Schneider, 1999 Display Technologies CRT (Cathode Ray Tube) LCD (Liquid Crystal Display) Computer Graphics – Week 12 © Bengt-Olaf Schneider, 1999 CRT: Basic Structure (1) Top View Vertical Deflection Collector Control Grid System Electrode Phosphor Electron Beam Cathode Electron Lens Horizontal Deflection System Computer Graphics – Week 12 © Bengt-Olaf Schneider, 1999 CRT: Basic Structure (2) Deflection System Typically magnetic and not electrostatic Reduces the length of the tube and allows wider Vertical Deflection Collector deflection angles Control Grid System Electrode Phosphor Phospor Electron Beam Cathode Electron Lens Horizontal Fluorescence: Light emitted Deflection System after impact of electrons Persistence: Duration of emission after beam is turned off. Determines flicker properties of the CRT. Computer Graphics – Week -

Chapter 2 Fundamentals of Digital Imaging
Chapter 2 Fundamentals of Digital Imaging Part 4 Color Representation © 2016 Pearson Education, Inc., Hoboken, 1 NJ. All rights reserved. In this lecture, you will find answers to these questions • What is RGB color model and how does it represent colors? • What is CMY color model and how does it represent colors? • What is HSB color model and how does it represent colors? • What is color gamut? What does out-of-gamut mean? • Why can't the colors on a printout match exactly what you see on screen? © 2016 Pearson Education, Inc., Hoboken, 2 NJ. All rights reserved. Color Models • Used to describe colors numerically, usually in terms of varying amounts of primary colors. • Common color models: – RGB – CMYK – HSB – CIE and their variants. © 2016 Pearson Education, Inc., Hoboken, 3 NJ. All rights reserved. RGB Color Model • Primary colors: – red – green – blue • Additive Color System © 2016 Pearson Education, Inc., Hoboken, 4 NJ. All rights reserved. Additive Color System © 2016 Pearson Education, Inc., Hoboken, 5 NJ. All rights reserved. Additive Color System of RGB • Full intensities of red + green + blue = white • Full intensities of red + green = yellow • Full intensities of green + blue = cyan • Full intensities of red + blue = magenta • Zero intensities of red , green , and blue = black • Same intensities of red , green , and blue = some kind of gray © 2016 Pearson Education, Inc., Hoboken, 6 NJ. All rights reserved. Color Display From a standard CRT monitor screen © 2016 Pearson Education, Inc., Hoboken, 7 NJ. All rights reserved. Color Display From a SONY Trinitron monitor screen © 2016 Pearson Education, Inc., Hoboken, 8 NJ. -

Computational RYB Color Model and Its Applications
IIEEJ Transactions on Image Electronics and Visual Computing Vol.5 No.2 (2017) -- Special Issue on Application-Based Image Processing Technologies -- Computational RYB Color Model and its Applications Junichi SUGITA† (Member), Tokiichiro TAKAHASHI†† (Member) †Tokyo Healthcare University, ††Tokyo Denki University/UEI Research <Summary> The red-yellow-blue (RYB) color model is a subtractive model based on pigment color mixing and is widely used in art education. In the RYB color model, red, yellow, and blue are defined as the primary colors. In this study, we apply this model to computers by formulating a conversion between the red-green-blue (RGB) and RYB color spaces. In addition, we present a class of compositing methods in the RYB color space. Moreover, we prescribe the appropriate uses of these compo- siting methods in different situations. By using RYB color compositing, paint-like compositing can be easily achieved. We also verified the effectiveness of our proposed method by using several experiments and demonstrated its application on the basis of RYB color compositing. Keywords: RYB, RGB, CMY(K), color model, color space, color compositing man perception system and computer displays, most com- 1. Introduction puter applications use the red-green-blue (RGB) color mod- Most people have had the experience of creating an arbi- el3); however, this model is not comprehensible for many trary color by mixing different color pigments on a palette or people who not trained in the RGB color model because of a canvas. The red-yellow-blue (RYB) color model proposed its use of additive color mixing. As shown in Fig. -

Switchable Primaries Using Shiftable Layers of Color Filter Arrays
Switchable Primaries Using Shiftable Layers of Color Filter Arrays Behzad Sajadi ∗ Kazuhiro Hiwadaz Atsuto Makix Ramesh Raskar{ Aditi Majumdery Toshiba Corporation Toshiba Research Europe Camera Culture Group University of California, Irvine Cambridge Laboratory MIT Media Lab RGB Camera Our Camera Ground Truth Our Camera CMY Camera RGB Camera 8.14 15.87 Dark Scene sRGB Image 17.57 21.49 ∆E Difference ∆E Bright Scene CMY Camera Our Camera (2.36, 9.26, 1.96) (8.12, 29.30, 4.93) (7.51, 22.78, 4.39) Figure 1: Left: The CMY mode of our camera provides a superior SNR over a RGB camera when capturing a dark scene (top) and the RGB mode provides superior SNR over CMY camera when capturing a lighted scene. To demonstrate this, each image is marked with its quantitative SNR on the top left. Right: The RGBCY mode of our camera provides better color fidelity than a RGB or CMY camera for colorful scene (top). The DE deviation in CIELAB space of each of these images from a ground truth (captured using SOC-730 hyperspectral camera) is encoded as grayscale images with error statistics (mean, maximum and standard deviation) provided at the bottom of each image. Note the close match between the image captured with our camera and the ground truth. Abstract ment of the primaries in the CFA) to provide an optimal solution. We present a camera with switchable primaries using shiftable lay- We investigate practical design options for shiftable layering of the ers of color filter arrays (CFAs). By layering a pair of CMY CFAs in CFAs. -

Primary Color | 23
BRAND Style GuiDe PriMary Color | 23 PRIMARY COLOR The primary color for Brandeis IBS is Brandeis IBS Blue, which is also the color of Brandeis University. Brandeis IBS Blue is BrandeiS iBS BLUE to be used as the prominent color in all communications. The PANTONE 294 C primary color is ideal for use in: CMYK 100 | 86 | 14 | 24 • Headlines • Large areas of text RGB 0 | 46 | 108 • Large background shapes HEX #002E6C Always use the designated color values for physical and digital Brandeis IBS communications. WEB HEX for use with white backgrounds #002E6C DO NOT use a tint of the primary color. Always use the primary color at 100% saturation. PANTONE color is used in physical applications whenever possible to reinforce the visual brand identity. CMYK designation is used for physical applications as an alternative to PANTONE (with the exception of any Microsoft Office documents, which use RGB). RGB values are used for any digital communications (excluding websites and e-communications), and all Microsoft Office documents (physical or digital). HEX values are used for any digital communications (excluding websites and e-communications). The value is an exact match to RGB. WEB HEX values are designated so websites and e-communica- tions can meet accessibility requirements. This compliance will ensure that people with disabilities can use Brandeis IBS online communications. For more about accessibility, visit http://www.brandeis.edu/acserv/disabilities/index.html. For examples of how the primary color should be applied across communications, please see pages 30-44. BRAND Style GuiDe SeCondary Color | 24 SeCondary Color The secondary color for Brandeis IBS is Brandeis IBS Teal, which is to be used strongly throughout Brandeis IBS com- BrandeiS iBS teal munications. -

Visualizing the Novel Clinton Mullins Connecticut College, [email protected]
Connecticut College Digital Commons @ Connecticut College Computer Science Honors Papers Computer Science Department 2013 Visualizing the Novel Clinton Mullins Connecticut College, [email protected] Follow this and additional works at: http://digitalcommons.conncoll.edu/comscihp Part of the Computer Sciences Commons Recommended Citation Mullins, Clinton, "Visualizing the Novel" (2013). Computer Science Honors Papers. 4. http://digitalcommons.conncoll.edu/comscihp/4 This Honors Paper is brought to you for free and open access by the Computer Science Department at Digital Commons @ Connecticut College. It has been accepted for inclusion in Computer Science Honors Papers by an authorized administrator of Digital Commons @ Connecticut College. For more information, please contact [email protected]. The views expressed in this paper are solely those of the author. Visualizing Novelthe kiss me please Thesis and code written by Clint Mullins with Professor Bridget Baird as the project's faculty advisor. 1. Data Visualization Discussion of data visualization. 2. Visualizing the Novel Introduction to our problem and execution overview. 3. Related Works Technologies and libraries used for the project. .1 Semantic Meaning .2 Parsing Text .3 Topic Modeling .4 Other Visualizations 4. Methods Specific algorithms and execution details. .1 Gunning FOG Index .2 Character Extraction .3 Character Shaping .4 Gender Detection .5 Related Word Extraction .6 Moments / Emotion Spectrum / DISCO 5. The Visual Our visual model from conception to completion. .1 Concept Process .2 Current Visual Model .3 Java2D .4 Generalizing the Visual Model 6. Results Judging output on known texts. .1 Text One – Eternally .2 Text Two – Love is Better the Second Time Around .3 How Successful is This? 7. -

Color Appearance Models Today's Topic
Color Appearance Models Arjun Satish Mitsunobu Sugimoto 1 Today's topic Color Appearance Models CIELAB The Nayatani et al. Model The Hunt Model The RLAB Model 2 1 Terminology recap Color Hue Brightness/Lightness Colorfulness/Chroma Saturation 3 Color Attribute of visual perception consisting of any combination of chromatic and achromatic content. Chromatic name Achromatic name others 4 2 Hue Attribute of a visual sensation according to which an area appears to be similar to one of the perceived colors Often refers red, green, blue, and yellow 5 Brightness Attribute of a visual sensation according to which an area appears to emit more or less light. Absolute level of the perception 6 3 Lightness The brightness of an area judged as a ratio to the brightness of a similarly illuminated area that appears to be white Relative amount of light reflected, or relative brightness normalized for changes in the illumination and view conditions 7 Colorfulness Attribute of a visual sensation according to which the perceived color of an area appears to be more or less chromatic 8 4 Chroma Colorfulness of an area judged as a ratio of the brightness of a similarly illuminated area that appears white Relationship between colorfulness and chroma is similar to relationship between brightness and lightness 9 Saturation Colorfulness of an area judged as a ratio to its brightness Chroma – ratio to white Saturation – ratio to its brightness 10 5 Definition of Color Appearance Model so much description of color such as: wavelength, cone response, tristimulus values, chromaticity coordinates, color spaces, … it is difficult to distinguish them correctly We need a model which makes them straightforward 11 Definition of Color Appearance Model CIE Technical Committee 1-34 (TC1-34) (Comission Internationale de l'Eclairage) They agreed on the following definition: A color appearance model is any model that includes predictors of at least the relative color-appearance attributes of lightness, chroma, and hue. -

ARC Laboratory Handbook. Vol. 5 Colour: Specification and Measurement
Andrea Urland CONSERVATION OF ARCHITECTURAL HERITAGE, OFARCHITECTURALHERITAGE, CONSERVATION Colour Specification andmeasurement HISTORIC STRUCTURESANDMATERIALS UNESCO ICCROM WHC VOLUME ARC 5 /99 LABORATCOROY HLANODBOUOKR The ICCROM ARC Laboratory Handbook is intended to assist professionals working in the field of conserva- tion of architectural heritage and historic structures. It has been prepared mainly for architects and engineers, but may also be relevant for conservator-restorers or archaeologists. It aims to: - offer an overview of each problem area combined with laboratory practicals and case studies; - describe some of the most widely used practices and illustrate the various approaches to the analysis of materials and their deterioration; - facilitate interdisciplinary teamwork among scientists and other professionals involved in the conservation process. The Handbook has evolved from lecture and laboratory handouts that have been developed for the ICCROM training programmes. It has been devised within the framework of the current courses, principally the International Refresher Course on Conservation of Architectural Heritage and Historic Structures (ARC). The general layout of each volume is as follows: introductory information, explanations of scientific termi- nology, the most common problems met, types of analysis, laboratory tests, case studies and bibliography. The concept behind the Handbook is modular and it has been purposely structured as a series of independent volumes to allow: - authors to periodically update the