People and Events Behind the Fractal Images
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Stone Soup Spring 2019
Spring 2019 & Spring Classes Catalogue The Journal of the San Geronimo Valley Community Center Rolling Stones St. Patrick’s Day by Dave Cort, Executive Director Youth Talent Show By Howie Cort Community Center “We Have a Really Big Shew Tonight” - Ed Sullivan th 50 Anniversary Year First there was The Ed Sullivan Show on Sunday nights. Then there was America’s Got Talent, followed by American Idol, but none of these shows can compare to our sweet, down-home, annual St. Patrick’s Day Talent Show. If you have been to this event you know what I’m talking about. Our Valley kids get up on the stage and open themselves Honoring The Past and their hearts to the audience by singing, dancing, reciting poetry, telling stories, jokes, and playing their instruments. It is an evening where our community of family and friends gather together to celebrate what’s really important: the children and youth Embracing The Present of our Valley. The evening is set up in three parts. The younger kids, between the ages of 5 to 10, will perform in the first act that will start at 4 p.m. and last until 5 p.m. We will take a break and, for an additional fee, you can enjoy a delicious dinner, along with Planning For The Future beverages and sweets. At 6 p.m., the second half will begin with the older kids. Instead of Ed Sullivan, we have MC extraordinaire Jasper Thelin and his amazing assistant Alexander McQuilkin who will entertain the audience and introduce the acts for the It is such an honor for me to be serving as Executive Director of the San Geronimo Valley show. -

GOAL Global Opportunity Asset Locator Outlook for 2021 Rotation
20 November 2020 | 5:46PM GMT GOAL: Global Opportunity Asset Locator Outlook for 2021: Rotation inoculation — remain pro-risk Christian Mueller-Glissmann, CFA +44(20)7774-1714 | christian.mueller- [email protected] Goldman Sachs International Alessio Rizzi n We are pro-risk for 2021 and expect the pro-cyclical rotation across and within +44(20)7552-3976 | [email protected] assets to continue, supported by a strong economic recovery from the COVID-19 Goldman Sachs International Cecilia Mariotti shock. With a favourable growth/inflation mix and still elevated equity risk premia +44(20)7552-0450 | [email protected] we are OW equities and UW bonds. With tighter credit spreads we are N credit Goldman Sachs International but still see opportunities to move down in quality. Over a 12m horizon we are Andrea Ferrario +44(20)7552-4353 | OW commodities (N for 3m), supported in particular by a bullish oil view. [email protected] Goldman Sachs International n While absolute equity valuations are high after the sharp recovery, they remain Peter Oppenheimer +44(20)7552-5782 | attractive vs. bonds. And equities should be able to digest a gradual increase in [email protected] bond yields better than fixed income as long as they come alongside better Goldman Sachs International David J. Kostin growth. We expect more rotation within equities – the leadership in regions, +1(212)902-6781 | [email protected] sectors and styles has been unusually defensive in the recovery. Goldman Sachs & Co. LLC Kathy Matsui n Our Risk Appetite Indicator (RAI) has turned positive, which alone is not a +81(3)6437-9950 | [email protected] Goldman Sachs Japan Co., Ltd. -

Rich Corporations Poor Societies
Rich corporations, poor societies: The financialisation of Apple By Rodrigo Fernandez (SOMO) and Reijer Hendrikse October 2015 Contents 1 Introduction ..................................................................................................... 3 2 Corporate financialisation .................................................................................. 5 3 The financialisation of Apple ............................................................................10 3.1 A short overview ......................................................................................10 3.2 Offshoring/outsourcing production ...............................................................12 3.3 Offshoring paper trails ...............................................................................13 3.4 Apple’s cash pile ......................................................................................15 3.5 A corporate cash machine .........................................................................17 4 Conclusion .....................................................................................................19 Glossary .............................................................................................................21 Colophon ............................................................................................................22 1 Introduction At the dawn of the new millennium, Apple Inc. stands as the epitome of a digitalised and globalised economy shaped by information and communication technologies. A world -

HUL, HUL.U Harvest US Equity Plus Income
Harvest US Equity Plus Income ETF HUL, HUL.U Meeting Date Range: 01-Jul-2019 - 30-Jun-2020 Proxy Voting Report APPLE INC. Security: 037833100 Agenda Number: 935121563 Ticker: AAPL Meeting Type: Annual ISIN: US0378331005 Meeting Date: 2/26/2020 Prop. # Proposal Proposed by Proposal Vote For/Against Management's Recommendation 1A. Election of Director: James Bell Mgmt For For 1B. Election of Director: Tim Cook Mgmt For For 1C. Election of Director: Al Gore Mgmt For For 1D. Election of Director: Andrea Jung Mgmt For For 1E. Election of Director: Art Levinson Mgmt For For 1F. Election of Director: Ron Sugar Mgmt For For 1G. Election of Director: Sue Wagner Mgmt For For 2. Ratification of the appointment of Ernst & Mgmt For For Young LLP as Apple's independent registered public accounting firm for 2020 3. Advisory vote to approve executive Mgmt For For compensation 4. A shareholder proposal entitled "Shareholder Shr Against For Proxy Access Amendments" 5. A shareholder proposal relating to Shr Against For sustainability and executive compensation 6. A shareholder proposal relating to policies on Shr Against For freedom of expression APPLIED MATERIALS, INC. Security: 038222105 Agenda Number: 935126258 Ticker: AMAT Meeting Type: Annual ISIN: US0382221051 Meeting Date: 3/12/2020 Prop. # Proposal Proposed by Proposal Vote For/Against Management's Recommendation 1A. Election of Director: Judy Bruner Mgmt For For 1B. Election of Director: Xun (Eric) Chen Mgmt For For 1C. Election of Director: Aart J. de Geus Mgmt For For 1D. Election of Director: Gary E. Dickerson Mgmt For For 1E. Election of Director: Stephen R. -

Apple Finance Chief Retiring (Update) 4 March 2014
Apple finance chief retiring (Update) 4 March 2014 Maestri joined Apple in March of last year and was said to already be managing most of the California- based company's financial matters. Maestri's professional background spans more than 25 years and includes stints as chief financial officer at Xerox and Nokia Siemens Networks, now called Nokia Solutions and Networks, according to Apple. "I am confident he will be a great CFO at Apple," Cook said of Maestri. "When we were recruiting for a corporate controller, we met Luca and knew he would become Peter's In this Tuesday, May 21, 2013, file photo, Apple chief successor." financial officer Peter Oppenheimer, testifies on Capitol Hill in Washington. Oppenheimer will retire in September Oppenheimer said in a release that after 18 years 2014 and will be replaced by the company's corporate working at Apple, he was going to take time for controller. The announcement Tuesday, March 4, 2014, himself and his family. His stated plans for the comes one day after Goldman Sachs named future included traveling the world and completing Oppenheimer as one of its 13 board members. (AP the requirements for a pilot's license. Photo/J. Scott Applewhite, File) © 2014 AFP Apple on Tuesday announced that the chief finance officer who served during the company's meteoric rise over the past decade is retiring later this year. Peter Oppenheimer will leave in September, turning the position over to Luca Maestri, according to the maker of iPhones, iPads, iPods and Macintosh computers. "Peter has served as our CFO for the past decade as Apple's annual revenue grew from $8 billion to $171 billion and our global footprint expanded dramatically," Apple chief executive Tim Cook said in a release. -

Case Study: Where Have All the Processors Gone?
The Synergist: How to Lead Your Team to Predictable Success Case Study: Where Have All The Processors Gone? It’s hard to find a good, single, stand alone case study for a Processor. It’s not that they are less common than Visionaries or Operators. It’s just that by the very nature of who they are, they eschew the limelight. They prefer to work behind the scenes making sure the systems and processes are in place to allow good organizations to become great organizations. They care little about seeking public praise or adulation. You don’t often see a Processor striding up and down the stage at the annual company retreat, representing the business at a charity event or giving interviews to the local news station. Instead you’ll be more likely to find them making sure that what the company does today is repeatable, consistent and scalable tomorrow and into the future. In many ways they are the unsung hero of our three natural styles. That’s not to say there aren’t examples of them out in the wild. And it’s not to say that at times we wouldn’t want a Processor in charge. We shouldn’t conflate the cult of the Visionary or the get it done mentality of the Operator with good leadership. Yes, quite often, particularly during the early stages of a company’s growth we need a good V or O in charge. But there are occasions when we need the structured, methodical thinking of a P to put in place the systems and processes needed to stable the ship and get us sailing in the right direction again. -

Another Giant Mining Fortune Represented in the Pilgrims Society (History’S Biggest Pandora’S Box!)
ANOTHER GIANT MINING FORTUNE REPRESENTED IN THE PILGRIMS SOCIETY (HISTORY’S BIGGEST PANDORA’S BOX!) Presented October 2017 by Charles Savoie Refused coverage by Dave Janda, Greg Hunter, And dozens of “alt media” You Tube channels! Refused coverage by 24 Hour Gold, Silver Seek, And the rest of the “Ha-Ha” Parade! (Save this in your Downloads File; read in several sessions.) In April we reviewed details on James Ben Ali Haggin (1827- 1914, Episcopalian; Pilgrims Society member known as “the greatest mine owner on earth”) in “Silver Mining Kingpin Opposed Silver Money.” In August we reviewed the Guggenheim mining dynasty in “Vast Mining Fortune Represented in Pilgrims Society World Money Trust.” This item will be about the South Africa Oppenheimer mining fortune (diamonds, gold, platinum, uranium, titanium, zinc, copper, cobalt, coal, chemicals, manganese, rhodium, nickel, iron etc.) and there was a marriage in 1660 between the Guggenheims and Oppenheimers, back in the Old World. Not only that, but Jakob Oppenheimer ran a bank at Hanover, Germany, where the first Rothschild was an apprentice during 1757-1763! Samuel Oppenheimer (1630-1703) was military supplier to King Leopold I of Hungary, Croatia and Bohemia. The Guggenheims appear to have mostly died out and those still bearing that name being of lesser influence, the fortune shifting into Episcopalian hands (The Lawson-Johnstons, Episcopalians and Pilgrims Society members). I realize those releases were way longer than most metals investors are used to reading (539 pages together) but the background on Haggin, the Guggenheims and the Lawson-Johnstons is extensive, and in fact, I only provided a basic outline on both. -

Halaman Judul Halaman Pengesahan Pembimbing
PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI HALAMAN JUDUL PENGARUH KUALITAS PRODUK, HARGA, DAN PROMOSI TERHADAP KEPUTUSAN PEMBELIAN SMARTPHONE IPHONE (studi kasus konsumen Iphone di kampus 1 Universitas Sanata Dharma) Skripsi Diajukan dalam Rangka Menulis Skripsi Program Studi Manajemen, Jurusan Manajemen Fakultas Ekonomi Universitas Sanata Dharma Oleh : Leonardus Niko Andira NIM: 152214089 PROGRAM STUDI MANAJEMEN JURUSAN MANAJEMEN FAKULTAS EKONOMI UNIVERSITAS SANATA DHARMA YOGYAKARTA 2019 HALAMAN PENGESAHAN PEMBIMBING PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI HALAMAN JUDUL PENGARUH KUALITAS PRODUK, HARGA, DAN PROMOSI TERHADAP KEPUTUSAN PEMBELIAN SMARTPHONE IPHONE (studi kasus konsumen Iphone di kampus 1 Universitas Sanata Dharma) Skripsi Diajukan dalam Rangka Menulis Skripsi Program Studi Manajemen, Jurusan Manajemen Fakultas Ekonomi Universitas Sanata Dharma Oleh : Leonardus Niko Andira NIM: 152214089 PROGRAM STUDI MANAJEMEN JURUSAN MANAJEMEN FAKULTAS EKONOMI UNIVERSITAS SANATA DHARMA YOGYAKARTA 2019 HALAMAN PENGESAHAN PEMBIMBING i PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI Moto dan Persembahan “Kamu harus bisa menghibur dirimu, karena kebahagian tidak datang dari manapun melainkan dari dalam dirimu sendiri” (CakNun) “Apa yang membuatmu bahagia lakukanlah dan apa yang membuatmu bersedih tinggalkan” Skripsi ini saya persembahkan untuk : Tuhan Yesus Kristus dan Bunda Maria yang selalu memberkati saya dalam mengerjakan skripsi dari awal hingga selesai. Ayah dan -

Oxford Magazine, Unacceptable to It”, with the Result That the Original Mo- No 384, 2Nd Week, TT 2017)
OXFORDmagazine No. 397 Fifth Week Trinity Term 2018 Congregation has been unusually in our much-esteemed ‘self-govern- active over the last three years, but ance’. not notably effective. In February The question has gained height- 2015 there was an impasssioned de- ened relevance in light of the last bate on the Castle Mill graduate flats minute formal, e-mailed cancellation on Port Meadow, which included of a Congregation meeting scheduled an admission of, and apology for, Meaningful for 15th May (4th week). The intended inadequacies in planning from the motion, announced in good time in Registrar. Then there were a series the Gazette of 26th April, sought to of principled debates on what might self-governance include specially elected members of have seemed a matter of limited in- Congregation, drawn from constitu- terest or concern for most Congre- encies whose interests are insuffi- gation members, the EJRA. Council ciently represented by Council, in the arranged the sequence of events in membership of Council’s self-review, such a way that an extra – and in effect pointless – Con- due to take place over the summer. As announced in the gregation meeting had to be called: moreover, contrary Gazette of 26th April, Council at its meeting on 23rd April to normal practice amendments had to be announced took the position that it “regarded the resolution to be electronically rather than in print (see Oxford Magazine, unacceptable to it”, with the result that the original mo- No 384, 2nd Week, TT 2017). At the end of TT 2017 tion would be opposed and voted upon. -

Global Macro Research Top of Mind March 11, 2014 Issue 21
Global Macro Research Top of Mind March 11, 2014 Issue 21 All About Bitcoin From the editor: News about Bitcoin seems to be everywhere. So what is it? The short answer is that Bitcoin with a capital “B” is a peer-to-peer network that allows for the proof and transfer of ownership without the need for a trusted third party. The unit of that network is bitcoin with a little “b”. But agreement on the topic seems to end there; indeed, there is a deep divide between true Bitcoin believers and serious skeptics. We look at the range of wildly diverging views. So where does that leave us? With the conclusion that bitcoin likely can’t work as a currency, but some sense that the ledger- based technology that underlies it could hold promise. Inside Interview with Eric Posner 4 Professor of Law, University of Chicago Is bitcoin a currency? No. 6 Dominic Wilson /Jose Ursua, GS Markets Research Bullion bests bitcoin, not Bitcoin 7 Jeff Currie, GS Commodities Research Interview with Fred Ehrsam 8 Co-Founder, Coinbase Interview with Ken Hess 10 IT specialist and author, ZD-net.com Interview with Dmitry Dain 14 CTO and Founder, Betalabs LLC Interview with Perkins Coie 16 Dax Hansen, Partner; Jacob Farber, Senior Counsel Is Bitcoin the future of payments? 18 Roman Leal, GS IT Services Equity Research Interview with Daniel Masters 20 Co-Principal, Global Advisors Source: www.istockphoto.com There is no question that the The core technological [Bitcoin] would not be a most vulnerable point of the problem that [Bitcoin] has solved good substitute [for fiat -
A Forest of Cactus: the Dunlap Collection
LOTUSLAND NEWSLETTER VOLUME 26 NO. 3SUMMER 2017 A Forest of Cactus: The Dunlap Collection BY PAUL MILLS I have received many strange letters at one time or another from all over the world but yours, I am sure, was the strangest of all. —Ganna Walska, August 1, 1966 OUR DAYS PRIOR, Merritt “Sigs” Dunlap sat at his typewriter and Fcrafted this “strange” letter to Madame Ganna Walska that would set in motion the creation of one of the great displays of cacti in a public garden and one of the most dramatic gardens at Lotusland—The Dunlap Cactus Garden. The letter stated that he wanted to be- queath his cactus collection to Lotusland. In 1966, Merritt Dunlap, or “Sigs” to his friends, had been developing his cactus collection for 37 years, which was near its peak with “approximately 1200 plants, of 880 species and varieties.” Sigs got his first plant in 1929 and his last in 1999—70 years of The Cactus Garden at Lotusland embodies the collaborative genius of a devoted collector, a visionary horticultural history. His passion was designer, numerous botanical experts and imaginative donors all coming together to create an iconic Continued on page 2 garden that could only exist at Ganna Walska Lotusland. IN THIS ISSUE A Forest of Cactus: The Dunlap 1 Forces of Nature 9 Fall Harvest Dinner 15 A Lotusland Food and Wine Fête Collection Benefit Shopping Extravaganza9 Exceptional Plants 15 Director’s Letter 4 Honoring Members of 10 Lotusland Auction and Sale C Magazine Features Lotusland 4 The Lotus Society The Spirit of Lotusland 15 Horticultural Happenings -
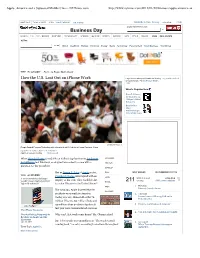
Apple, America and a Squeezed Middle Class - Nytimes.Com
Apple, America and a Squeezed Middle Class - NYTimes.com http://www.nytimes.com/2012/01/22/business/apple-america-an... HOME PAGE TODAY'S PAPER VIDEO MOST POPULAR U.S. Edition Subscribe to Home Delivery erika.allen... Help Search All NYTimes.com Business Day WORLD U.S. N.Y. / REGION BUSINESS TECHNOLOGY SCIENCE HEALTH SPORTS OPINION ARTS STYLE TRAVEL JOBS REAL ESTATE AUTOS Global DealBook Markets Economy Energy Media Technology Personal Tech Small Business Your Money THE iECONOMY Part 1: An Empire Built Abroad How the U.S. Lost Out on iPhone Work Log in to see what your friends are sharing Log In With Facebook on nytimes.com. Privacy Policy | What’s This? What’s Popular Now Russell Johnson, the Professor on ‘Gilligan’s Island,’ Dies at 89 Baryshnikov Plans Fund-Raising to Give Artists Space Donald Chan/Reuters People flooded Foxconn Technology with résumés at a 2010 job fair in Henan Province, China. By CHARLES DUHIGG and KEITH BRADSHER Published: January 21, 2012 778 Comments When Barack Obama joined Silicon Valley’s top luminaries for dinner FACEBOOK in California last February, each guest was asked to come with a TWITTER question for the president. GOOGLE+ But as Steven P. Jobs of Apple spoke, SAVE MOST EMAILED RECOMMENDED FOR YOU THE iECONOMY President Obama interrupted with an EMAIL A series examining challenges articles viewed erika.allen inquiry of his own: what would it take recently All Recommendations posed by increasingly globalized SHARE 211 high-tech industries. to make iPhones in the United States? PRINT 1. EDITORIAL Dissent, Guns & Ammo Not long ago, Apple boasted that its REPRINTS products were made in America.