Approximate Solutions for HBV Infection with Stability Analysis Using LHAM During Antiviral Therapy
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
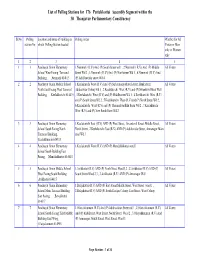
List of Polling Stations for 176 Pattukkottai Assembly Segment Within the 30 Thanjavur Parliamentary Constituency
List of Polling Stations for 176 Pattukkottai Assembly Segment within the 30 Thanjavur Parliamentary Constituency Sl.No Polling Location and name of building in Polling Areas Whether for All station No. which Polling Station located Voters or Men only or Women only 12 3 4 5 1 1 Panchayat Union Elementary 1.Nemmeli ( R.V) And (P) South Street wd 1 , 2.Nemmeli ( R.V) And (P) Middle All Voters School West Facing Terraced Street Wd 2 , 3.Nemmeli ( R.V) And (P) Northstreet Wd 3 , 4.Nemmeli ( R.V) And Building, ,Nemmeli 614015 (P) Adi Dravidar street Wd 4 2 2 Panchayat Union Middle School 1.Keelakurichi West (R.V) And (P) Subramaniyarkovil street, Bank street, All Voters North East Facing West Terraced Adidravidar Colony wd 1 , 2.Keelakurichi West (R.V) and (P) Sivankovil Steet Wd 1 Building, ,Keelakkurichi 614015 , 3.Keelakurichi West (R.V) and (P) Middlestreet Wd 1 , 4.Keelakurichi West (R.V) and (P) South Street Wd 2 , 5.Keelakurichi West (R.V) and (P) North Street Wd 2 , 6.Keelakurichi West (R.V) and (P) Thenmelavadkku theru Wd 2 , 7.Keelakurichi West (R.V) and (P) New South Steet Wd 2 3 3 Panchayat Union Elementay 1.Keelakurichi East (R.V) AND (P) West Street, Sivankovil Street, Middle Street, All Voters School South Facing North North Street , 2.Keelakurichi East (R.V) AND (P) Adidravidar Street, Annanagar Main Terrraced Building, road Wd 3 ,Keelakkurichi 614015 4 4 Panchayat Union Elementary 1.Keelakurichi West (R.V) AND (P) Mandalakkottai ward 1 All Voters School South Building East Facing, ,Mandalakkottai 614015 5 5 Panchayat Union -

University Departments
LIST OF COLLEGES TNEA Page S.No. Code Name of the College No. No UNIVERSITY DEPARTMENTS University Departments of Anna University, Chennai - CEG 1 0001 Campus, Sardar Patel Road, Guindy, Chennai 600 025 1 University Departments of Anna University, Chennai - ACT 2 0002 Campus, Sardar Patel Road, Guindy, Chennai 600 025 2 University Departments of Anna University, Chennai - SAP 3 0003 Campus, Sardar Patel Road, Guindy, Chennai 600 025 3 University Departments of Anna University, Chennai - MIT 4 0004 Campus, Chrompet, Tambaram Taluk, Kancheepuram District 600 4 044 Faculty of Engineering, Annamalai University, Annamalai Nagar, 5 0005 Chidamparam 608002 5 CONSTITUENT COLLEGES University College of Engineering, Villupuram, Kakuppam, 6 1013 Villupuram District 605103 6 University College of Engineering, Tindivanam, Melpakkam, 7 1014 Tindivanam, Villupuram District 604001 7 University College of Engineering, Arni, Arni to Devikapuram 8 1015 Road, Thatchur, Arni, Thiruvannamalai District 632326 8 University College of Engineering, Kancheepuram, Ponnerikarai 9 1026 Campus, NH4, Chennai-Bangalore Highway, Karaipettai Village 9 & Post, Kancheepuram District 631552 Anna University Regional Campus - Coimbatore, Maruthamalai 10 2025 Main Road, Navavoor Bharathiyar University Post, 105 Somayampalayam, Coimbatore District 641046 University College of Engineering, BIT Campus, Anna University, 11 3011 Tiruchirappalli District 620024 200 University College of Engineering, Ariyalur, Kathankudikadu 12 3016 Village, Thelur Post, Ariyalur District 621704 201 -

2020 Directorate of Technical Education, Chennai -25 Initial Vacancy Position - Academic
TAMILNADU ENGINEERING ADMISSIONS (TNEA) 2020 DIRECTORATE OF TECHNICAL EDUCATION, CHENNAI -25 INITIAL VACANCY POSITION - ACADEMIC COLLEGE NAME OF INSTITUTIONS BRANCH BRANCH NAME OC BC BCM MBC SC SCA ST Total CODE University Departments of Anna University, Chennai - CEG Campus, 1 BY Bio- Medical Engineering (SS) 17 15 2 12 8 2 1 57 Sardar Patel Road, Guindy, Chennai 600 025 University Departments of Anna University, Chennai - CEG Campus, 1 CE Civil Engineering 19 15 2 11 8 1 1 57 Sardar Patel Road, Guindy, Chennai 600 025 University Departments of Anna University, Chennai - CEG Campus, Computer Science and Engineering 1 CM 35 28 4 24 18 3 1 113 Sardar Patel Road, Guindy, Chennai 600 025 (SS) University Departments of Anna University, Chennai - CEG Campus, 1 CS Computer Science and Engineering 17 14 2 11 9 1 1 55 Sardar Patel Road, Guindy, Chennai 600 025 University Departments of Anna University, Chennai - CEG Campus, Electronics and Communication 1 EC 17 16 2 10 8 2 1 56 Sardar Patel Road, Guindy, Chennai 600 025 Engineering University Departments of Anna University, Chennai - CEG Campus, Electrical and Electronics 1 EE 18 15 2 11 9 2 1 58 Sardar Patel Road, Guindy, Chennai 600 025 Engineering University Departments of Anna University, Chennai - CEG Campus, Electronics and Communication 1 EM 34 31 4 24 17 4 1 115 Sardar Patel Road, Guindy, Chennai 600 025 Engg. (SS) University Departments of Anna University, Chennai - CEG Campus, 1 GI Geo-Informatics 10 10 1 8 6 1 1 37 Sardar Patel Road, Guindy, Chennai 600 025 University Departments of Anna University, Chennai - CEG Campus, 1 IE Industrial Engineering 11 9 1 8 6 1 0 36 Sardar Patel Road, Guindy, Chennai 600 025 University Departments of Anna University, Chennai - CEG Campus, 1 IM Information Tech. -

Private Schools Fee Determination Committee Chennai-600 006 - Fees Fixed for the Year 2013-2016 - District: Thanjavur Sl
PRIVATE SCHOOLS FEE DETERMINATION COMMITTEE CHENNAI-600 006 - FEES FIXED FOR THE YEAR 2013-2016 - DISTRICT: THANJAVUR SL. SCHOOL HEARING SCHOOL NAME & ADDRESS YEAR LKG UKG I II III IV V VI VII VIII IX X XI XII NO. CODE DATE Anuradha Mahavidyalaya 2013 - 14 5500 5500 6500 6500 6500 6500 6500 7200 7200 7200 8000 8000 - - Mat School Nalur, 1 230002 07-05-2013 2014 - 15 6050 6050 7150 7150 7150 7150 7150 7920 7920 7920 8800 8800 - - Thirucherai Post, Kumbakonam Tk, Thanjavur - 612 605. 2015 - 16 6655 6655 7865 7865 7865 7865 7865 8712 8712 8712 9680 9680 - - 2013 - 14 4500 4500 5000 5000 5000 5500 5500 5700 5700 5700 10000 10500 - - Royal Matriculatioon School, 2 230006 No.1,SNM Rahman Nagar, 19-03-2013 2014 - 15 4950 4950 5500 5500 5500 6050 6050 6270 6270 6270 11000 11550 - - East Gate, Thanjavur Dt-613 001 2015 - 16 5445 5445 6050 6050 6050 6655 6655 6897 6897 6897 12100 12705 - - Sri Venkateswara Vidiya 2013 - 14 5500 5500 7000 7000 7000 7000 7000 - - - - - - - Mandir Nursery & Primary School 3 230007 Thalikkottai, 12-03-13 2014 - 15 6050 6050 7700 7700 7700 7700 7700 - - - - - - - Nattuchalai Post Thanjavur Distirct - 614 906 2015 - 16 6655 6655 8470 8470 8470 8470 8470 - - - - - - - 2013 - 14 5200 5200 6000 6000 6000 6000 6000 - - - - - - - SWAMI DAYANANDA NURSERY & PRIMARY SCHOOL 4 23001 30-4-13 2014 - 15 5720 5720 6600 6600 6600 6600 6600 - - - - - - - PILLAIYARPATTI THANJAVUR 2015 - 16 6292 6292 7260 7260 7260 7260 7260 - - - - - - - 2013 - 14 5515 5515 6700 6700 6700 6700 6700 - - - - - - - AR- Rahman Nursery & Primary School, 5 230010 Periyar Nagar, 12-03-13 2014 - 15 6067 6067 7370 7370 7370 7370 7370 - - - - - - - Madukkur - 614 903 Thanja 2015 - 16 6674 6674 8107 8107 8107 8107 8107 - - - - - - - 2013 - 14 3400 3400 4450 4450 4450 4450 4450 - - - - - - - Imayam Nursery & Primary School 6 230017 Kanjha Nagar, 12-03-2013 2014 - 15 3740 3740 4895 4895 4895 4895 4895 - - - - - - - Rajagiri, Thanjavur - 614 207. -

Mint Building S.O Chennai TAMIL NADU
pincode officename districtname statename 600001 Flower Bazaar S.O Chennai TAMIL NADU 600001 Chennai G.P.O. Chennai TAMIL NADU 600001 Govt Stanley Hospital S.O Chennai TAMIL NADU 600001 Mannady S.O (Chennai) Chennai TAMIL NADU 600001 Mint Building S.O Chennai TAMIL NADU 600001 Sowcarpet S.O Chennai TAMIL NADU 600002 Anna Road H.O Chennai TAMIL NADU 600002 Chintadripet S.O Chennai TAMIL NADU 600002 Madras Electricity System S.O Chennai TAMIL NADU 600003 Park Town H.O Chennai TAMIL NADU 600003 Edapalayam S.O Chennai TAMIL NADU 600003 Madras Medical College S.O Chennai TAMIL NADU 600003 Ripon Buildings S.O Chennai TAMIL NADU 600004 Mandaveli S.O Chennai TAMIL NADU 600004 Vivekananda College Madras S.O Chennai TAMIL NADU 600004 Mylapore H.O Chennai TAMIL NADU 600005 Tiruvallikkeni S.O Chennai TAMIL NADU 600005 Chepauk S.O Chennai TAMIL NADU 600005 Madras University S.O Chennai TAMIL NADU 600005 Parthasarathy Koil S.O Chennai TAMIL NADU 600006 Greams Road S.O Chennai TAMIL NADU 600006 DPI S.O Chennai TAMIL NADU 600006 Shastri Bhavan S.O Chennai TAMIL NADU 600006 Teynampet West S.O Chennai TAMIL NADU 600007 Vepery S.O Chennai TAMIL NADU 600008 Ethiraj Salai S.O Chennai TAMIL NADU 600008 Egmore S.O Chennai TAMIL NADU 600008 Egmore ND S.O Chennai TAMIL NADU 600009 Fort St George S.O Chennai TAMIL NADU 600010 Kilpauk S.O Chennai TAMIL NADU 600010 Kilpauk Medical College S.O Chennai TAMIL NADU 600011 Perambur S.O Chennai TAMIL NADU 600011 Perambur North S.O Chennai TAMIL NADU 600011 Sembiam S.O Chennai TAMIL NADU 600012 Perambur Barracks S.O Chennai -

Localizing the Sustainable Development Goals of the Rajamadam Coastal Panchayat of the Pattukkottai Block, Thanjavur District
© 2020 IJRTI | Volume 5, Issue 2 | ISSN: 2456-3315 Localizing the Sustainable Development Goals of the Rajamadam Coastal Panchayat of the Pattukkottai Block, Thanjavur District 1T. Saravana Kumar 1Post Graduate student in 2 years Diploma on Development Management. B.Sc., Computer Science, Post Graduate Diploma in Development Management The DHAN Academy, Madurai, Tamil Nadu, India Abstract: Sustainable development goals (SDG) are universal agenda to make the world a better place to live. There are 17 goals and each goal have its own indicators. These SDGs were agreed by 193 countries in the world. The 193 countries are having its own unique characteristics, thus fixing the same indicators for all the goals may not help in achieving what is expected. Therefore, each country is expected to frame their goals regarding to their respective contexts. This is called as localization of the SDGs. In this study, 59 samples were assessed on eight goals of SDGs along with the indicators of Human Development report. From these indicators it was found that 26% of the families are extremely poor and 37% of the families are above the poverty. Health and concern regarding to the health is also poor, 66% of the families are having at least one person addicted to alcohol. Only 29% of the families are having good health practices. All the students (random sample) were in low BMI which shows malnutrition. Only those who have education could perform very well and were able to get out of the glitch of poverty. The education provided is also in bad shape. Out of 50 respondent families, 30% of children are dropouts. -

District Census Handbook, Thanjavur, Part X-A, Series-19
CENSUS OF INDIA, 1971 SERIES 19 TAMIL NADU PART X-A DISTRICT CENSUS HANDBOOK village and Town Directory THANJAVUR K. C HOC K A II N GAM of the Indian Administratire Service DIRECTOR OF CENSUS OPERATIONS. TAMIL NADU AND PONDICHERRY. 1972 jo Ang o 0 I I oj (/) L __________ -- o~~ ~ .., ~• II II II I .... ,: I·0 - -----_-----""- _...;.. -- CONTENTS Page No. Preface ... v Part-A VILLA GE AND TOWN DIRECTORY Introductory Note: vii-xiii (I) Village Directory ••• Amenities and land use Appendix-I Land use particulars of NOD - city urban area (Non-Municipal area) Appendix-II Abstr<lct showing Educationa), Medica1 aad other amenities available in Taluks. Alphabetical Jist of Villages. 1. Sirkali Taluk ... 2 -13 2. Mayuram ,. 14:- 35 S. Kumbakonam ,. 36 - 54 4:. Nannilam .. 55 - 84 5. Papanasam .. ... 85 -108 6. Thanjavur .. 109-134: 7. Orthanad 135-152 " ... 153 -172 8. Mannargudi .. '" 9. Nagapattinam .. - 173-190 191-210 10. Thiruthuraipundi " 11. Pattukkottai '0 211-234 12. Peravurani .. - 235-251 13. Arantangi ,. - 252-282 iv Page No. (II) Town Directory Statement: I - Status. Growth History and FunctIOnal Category of Tov.ns. 286 - 291 II - PhysIcal Aspects and Location of Towns, 1969. 292-297 lIt - Municipal Finance, 1968- 69 298-30:1 IV - Civic and other amenitle", 1969 304-309 , , V- Medical, Educational. Recreational and Cultural Facll.t1es in Towns. 1969 310 315 .. VI - Trade. Commerce. Industry and Banking, 1969 316- 321 ,. V/I- Population by rehgion. 1971 322-327 Maps f'i!'.trict map of Thanjavur Frontispiece PRf:FAGE It has been the practice since 1951 to publish for each District a Census Hand book, contaming the Census Statistics for each village and town in the Distnct together wIth certain administrative statistics collected from the various Departments of the State Government. -

Geography in Hong Kong (2012-16)
HONG KONG GEOGRAPHICAL ASSOCIATION 香 港 地 理 學 會 GEOGRAPHY IN HONG KONG (2012-16) A PROFILE OF GEOGRAPHY INSTITUTES, RESEARCHERS, KEY PUBLICATIONS AND OTHER GEOGRAPHY-RELATED ACTIVITIES June 2016 P.O. BOX 97553, TSIM SHA TSUI POST O FFICE KOWLOON, HONG KONG 1 WWW. HKGA.ORG Hong Kong Geographical Association 香 港 地 理 學 會 EXECUTIVE SUMMARY Hong Kong Geographical Association The Hong Kong Geographical Association Institutes & People (HKGA) was founded in 1969 with the aims of promoting interest in, stimulating teaching There are currently three departmental units of, and cultivating research about Geography. specialized in geography research and HKGA is led by an Executive Committee education in the tertiary institutes of Hong with honorary representatives from the Kong. In total, our community has over 70 tertiary institutions in Hong Kong. The teaching and research staff. They are recruited Association is the Hong Kong Sectional locally and internationally with diverse member of the International Geographical backgrounds. They are fully committed to Union. quality research and teaching, which are exemplified by their research outputs Over the years, HKGA has been promoting published in top ISI journals, professional geography education and research through a services offered in different institutional wide range of activities and services. Hong positions, and awards received. Kong Geography Day is the signature event for the Association, which aims to foster Research Excellence academic exchange and collaboration between geography-related faculty members and Geographers in Hong Kong are pursuing high postgraduate students, and to promote quality research in all directions and with local geography education in secondary schools. -

Journal of Pharmaceutical and Pharmacological Sciences Samuel P, Et Al., J Pharma Pharma Sci 02: JPPS-138
Journal of Pharmaceutical and Pharmacological Sciences Samuel P, et al., J Pharma Pharma Sci 02: JPPS-138. Research Article DOI: 10.29011/2574-7711.100038 Bioprospecting of Salicornia europaeaL. a Marine Halophyte and Evaluation of Its Biological Potential with Special Refer- ence to Anticancer Activity Samuel P1*, Vijaya J Kumar1, Deena R Dhayalan1, Amirtharaj K1, Sudarmani DNP2 1Department of Biotechnology, Ayya Nadar Janaki Ammal College(Autonomous), Sivakasi, TN, India 2Department of Zoology (PG), Ayya Nadar Janaki Ammal College (Autonomous), Sivakasi, TN, India *Corresponding author: Samuel P, Assistant Professor, Department of Biotechnology, Ayya Nadar Janaki Ammal College (Autono- mous), Sivakasi, TN, India. Tel: +919025559994; Email: [email protected] Citation: Samuel P, Kumar VJ, Dhayalan DR, Amirtharaj K, Sudarmani DNP (2017) Bioprospecting of Salicornia europaea L. a Marine Halophyte and Evaluation of Its Biological Potential with Special Reference to Anticancer Activity. J Pharma Pharma Sci 02: 138. DOI: 10.29011/2574-7711.100038 Received Date: 02 August, 2017; Accepted Date: 25 August, 2017; Published Date: 02 September, 2017 Abstract The present study was initiated with an intention to bring outthe phytochemical profile of the marine halophyte Salicornia europaeaL., the chemical finger print of the halophyte was made by GC-MS.The phytochemicalsin the crude extract was evalu- ated for cytotoxic study against MCF7. The marine halophytes were collected, washedand chopped in to 5cm long and shade dried for 20-25 days in a dark room. The dried and grounded plant materials were subjected to Soxhlet extraction.Two solvents vizmethanol and ethyl acetate were used to prepare decoction of the plant.The extracts were screened using GC-MS and dried us- ing rotary vacuum evaporator. -

Thanjavur District Date :13-07-2021 Local Body : Vaccination Proposal Nodel Nodel Actua Nodal PC 1435 Total TR
Statement 2 (LocalBody wise, Camp Wise) Thanjavur District Date :13-07-2021 Local Body : Vaccination Proposal Nodel Nodel Actua Nodal PC 1435 Total TR. Nodal NGO/ Assosi Assosi l Allotted Nodal Doctor Doctors S.No Local Body Camp Location Benefic SUNDARES Official Phone ation ation Achie Revenue Staff Police Doses Name Phone iery AN Number Perso Phone veme number 763914634 n No nt 3 PC 1435 TR. SUNDARESAN 7639146343 Thiruvaiyaru Naducauvery PHC Mrs. Shanthi (RI) 1 9442829979 Mohammed Pandhar Thiruvaiyaru Mrs.Manju (RI) PC 1160 TR.KRISHNAN 6379993079 2 (Thiruvalampozhil PHC) Mrs.Nandhi 9840217941 Vellamperambur Aided Middle ni BDO(VP) Thiruvaiyaru 7402607363 Mrs.Manju (RI) PC 1160 TR.KRISHNAN 6379993079 School (Thiruvalampozhil PHC) 3 600 600 Dr.Selvakumar 9.656E+09 9840217941 GRI 1035 TR. ASHOKKUMAR Arulprakasa Mrs.Manju (RI) Thiruvaiyaru Valapakudi VP (Senthalai PHC) 9486155611 9498112101 4 m SPL Tah. 9840217941 SSS GRI 1035 TR. ASHOKKUMAR Mrs.Manju (RI) Thiruvaiyaru Achanur (Senthalai PHC) 9498112101 5 9840217941 Thiruvaiyaru Kalyanapuram 1 Sethi Mrs.Manju (RI) PC 1160 TR.KRISHNAN 6379993079 6 (Thiruvalampozhil PHC) 9840217941 WPC 1078 John Sabeena 88707 Mrs.Amutha (RI) Thirupananthal 34615 7 Konullampallam PHC 1.Mr.Sivaku 9976430147 mar 7402607368 Pc 1673 Prabakaran 94981 21049 Thirupananthal Mrs.Amutha (RI) 8 Pandhanallur PHC BDO(VP) 9976430147 WPC 1110 suruthi915501 83118 Thirupananthal 730 730 Dr.A.Abinesh 8.668E+09 Mrs.Amutha (RI) 9 Keelakattur PHC 2.Mrs 9976430147 R.chitra WPC 545 Kiruthika 86750 03048 Thirupananthal Mr.Kumaraguru -

Choultries (Chattrams) Under the Marathas Rulers of Thanjavur Region
The International journal of analytical and experimental modal analysis ISSN NO: 0886-9367 Choultries (Chattrams) under the Marathas Rulers of Thanjavur Region T. SATHIYABAMA Ph.D. Research scholar Department of History Annamalai University Annamalai Nagar-608002 Tamil Nadu Cell : 9994878348 Historical Background in Thanjavur Region:- Thanjavur the Royal City of the Great Cholas, the Nayakas and Marathas which is one of the big towns in the State of Tamil Nadu and is situated on the main road of the Southern Railways, 351 K.m. South of Chennai. It considered being one of the oldest towns in the country having more than 200 years of its historical background. It is situated amidst the vast deltaic tract of the Cauvery known as the granary of South India. As the capital of the successive ancient Hindu Dynasties and in all ages one of the Chief Political, Literary and Religious Centre of South India this town is full of interesting associations. During the Nayakas period, the Kumbakonam region including Darassuram was considered as an important area . In the middle of the 17th century availing of the internal feuds between the Nayakas of Thanjavur and Madurai Venkanna, the Rayasam of Alagri sought the help of the Sultan of Bijapur for placing Sengamaladas at Nayak of Thanjavur.1The sultan sent Ekoji, son of Shahji, who had been stationed at Bangalore to proceed against Thanjavur, Ekoji defeated Alagiri and installed Sengamaladas as a ruler of Thanjavur. For that he Ekoji got revenues of following taluks namely Kumbakonam including Darasuram Papanasam and Mannarkudi .The nayakas of Thanjavur were succeeded by the Volume XI, Issue XI, November/2019 Page No:950 The International journal of analytical and experimental modal analysis ISSN NO: 0886-9367 marathas of Thanjavur. -

Influence of Seasons on Copepods of Agniyar Estuary, Palk Strait, Tamil Nadu, India J
International Journal of Zoology and Applied Biosciences ISSN: 2455-9571 Volume 1, Issue 1, pp: 40-45, 2016 http://www.ijzab.com Research Article INFLUENCE OF SEASONS ON COPEPODS OF AGNIYAR ESTUARY, PALK STRAIT, TAMIL NADU, INDIA J. Sugumaran* P.G. and Research Department of Zoology, Khadir Mohideen College, Adirampattinam-614701, Tamilnadu, India Article History: Received 2nd February 2017; Accepted 28th February 2016 ABSTRACT Seasonal variations of copepod diversity, density and physicochemical properties of Agniyar estuary was studied during 2014 and 2015. Physicochemical characteristics such as temperature, salinity, calcium and nitrite were high during premonsoon, while dissolved oxygen (DO) and nitrate were high during monsoon season. Copepods showed seasonal variations in diversity and density. Nineteen species of copepods belonging to 3 orders and 15 genera were reported. Density (1868 numbers/m3) was high during Postmonsoon, low diversity (948 numbers/m3) was recorded during monsoon. The marine and brackish water forms dominated during dry seasons while, the freshwater forms dominate rainy season. The study may serve as a basic platform for future studies and monitoring programmes of Agniyar estuary. Keywords: Agniyar Estuary, Zooplankton, Copepods, Seasonal changes. INTRODUCTION seasonal patterns of estuarine copepods with high taxonomic resolution in relation to hydrographic Estuarine ecosystems may be smaller, in terms of area and parameters. Further, the studies on zooplankton of Agniyar volume, but they provide a unique environment to their estuary are rather scanty except the study of rotifer biota by the mixing action of riverine and seawater diversity by Sugumaran and Amsath (2015). Hence the (Bienfang and Ziemann, 1992, Carlsson et al., 1995).