Chip-Seq of Transcription Factors Predicts Absolute and Differential Gene Expression in Embryonic Stem Cells
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Differences Between Human and Chimpanzee Genomes and Their Implications in Gene Expression, Protein Functions and Biochemical Properties of the Two Species Maria V
Suntsova and Buzdin BMC Genomics 2020, 21(Suppl 7):535 https://doi.org/10.1186/s12864-020-06962-8 REVIEW Open Access Differences between human and chimpanzee genomes and their implications in gene expression, protein functions and biochemical properties of the two species Maria V. Suntsova1 and Anton A. Buzdin1,2,3,4* From 11th International Young Scientists School “Systems Biology and Bioinformatics”–SBB-2019 Novosibirsk, Russia. 24-28 June 2019 Abstract Chimpanzees are the closest living relatives of humans. The divergence between human and chimpanzee ancestors dates to approximately 6,5–7,5 million years ago. Genetic features distinguishing us from chimpanzees and making us humans are still of a great interest. After divergence of their ancestor lineages, human and chimpanzee genomes underwent multiple changes including single nucleotide substitutions, deletions and duplications of DNA fragments of different size, insertion of transposable elements and chromosomal rearrangements. Human-specific single nucleotide alterations constituted 1.23% of human DNA, whereas more extended deletions and insertions cover ~ 3% of our genome. Moreover, much higher proportion is made by differential chromosomal inversions and translocations comprising several megabase-long regions or even whole chromosomes. However, despite of extensive knowledge of structural genomic changes accompanying human evolution we still cannot identify with certainty the causative genes of human identity. Most structural gene-influential changes happened at the level of expression regulation, which in turn provoked larger alterations of interactome gene regulation networks. In this review, we summarized the available information about genetic differences between humans and chimpanzees and their potential functional impacts on differential molecular, anatomical, physiological and cognitive peculiarities of these species. -

Plasma Cells in Vitro Generation of Long-Lived Human
Downloaded from http://www.jimmunol.org/ by guest on September 24, 2021 is online at: average * The Journal of Immunology , 32 of which you can access for free at: 2012; 189:5773-5785; Prepublished online 16 from submission to initial decision 4 weeks from acceptance to publication November 2012; doi: 10.4049/jimmunol.1103720 http://www.jimmunol.org/content/189/12/5773 In Vitro Generation of Long-lived Human Plasma Cells Mario Cocco, Sophie Stephenson, Matthew A. Care, Darren Newton, Nicholas A. Barnes, Adam Davison, Andy Rawstron, David R. Westhead, Gina M. Doody and Reuben M. Tooze J Immunol cites 65 articles Submit online. Every submission reviewed by practicing scientists ? is published twice each month by Submit copyright permission requests at: http://www.aai.org/About/Publications/JI/copyright.html Receive free email-alerts when new articles cite this article. Sign up at: http://jimmunol.org/alerts http://jimmunol.org/subscription http://www.jimmunol.org/content/suppl/2012/11/16/jimmunol.110372 0.DC1 This article http://www.jimmunol.org/content/189/12/5773.full#ref-list-1 Information about subscribing to The JI No Triage! Fast Publication! Rapid Reviews! 30 days* Why • • • Material References Permissions Email Alerts Subscription Supplementary The Journal of Immunology The American Association of Immunologists, Inc., 1451 Rockville Pike, Suite 650, Rockville, MD 20852 Copyright © 2012 by The American Association of Immunologists, Inc. All rights reserved. Print ISSN: 0022-1767 Online ISSN: 1550-6606. This information is current as of September 24, 2021. The Journal of Immunology In Vitro Generation of Long-lived Human Plasma Cells Mario Cocco,*,1 Sophie Stephenson,*,1 Matthew A. -

Investigation of Adiposity Phenotypes in AA Associated with GALNT10 & Related Pathway Genes
Investigation of Adiposity Phenotypes in AA Associated With GALNT10 & Related Pathway Genes By Mary E. Stromberg A Dissertation Submitted to the Graduate Faculty of WAKE FOREST UNIVERSITY GRADUATE SCHOOL OF ARTS AND SCIENCES in Partial Fulfillment of the Requirements for the Degree of DOCTOR OF PHILOSOPHY In Molecular Genetics and Genomics December 2018 Winston-Salem, North Carolina Approved by: Donald W. Bowden, Ph.D., Advisor Maggie C.Y. Ng, Ph.D., Advisor Timothy D. Howard, Ph.D., Chair Swapan Das, Ph.D. John P. Parks, Ph.D. Acknowledgements I would first like to thank my mentors, Dr. Bowden and Dr. Ng, for guiding my learning and growth during my years at Wake Forest University School of Medicine. Thank you Dr. Ng for spending so much time ensuring that I learn every detail of every protocol, and supporting me through personal difficulties over the years. Thank you Dr. Bowden for your guidance in making me a better scientist and person. I would like to thank my committee for their patience and the countless meetings we have had in discussing this project. I would like to say thank you to the members of our lab as well as the Parks lab for their support and friendship as well as their contributions to my project. Special thanks to Dean Godwin for his support and understanding. The umbrella program here at WFU has given me the chance to meet some of the best friends I could have wished for. I would like to also thank those who have taught me along the way and helped me to get to this point of my life, with special thanks to the late Dr. -

A Concise Review of Human Brain Methylome During Aging and Neurodegenerative Diseases
BMB Rep. 2019; 52(10): 577-588 BMB www.bmbreports.org Reports Invited Mini Review A concise review of human brain methylome during aging and neurodegenerative diseases Renuka Prasad G & Eek-hoon Jho* Department of Life Science, University of Seoul, Seoul 02504, Korea DNA methylation at CpG sites is an essential epigenetic mark position of carbon in the cytosine within CG dinucleotides that regulates gene expression during mammalian development with resultant formation of 5mC. The symmetrical CG and diseases. Methylome refers to the entire set of methylation dinucleotides are also called as CpG, due to the presence of modifications present in the whole genome. Over the last phosphodiester bond between cytosine and guanine. The several years, an increasing number of reports on brain DNA human genome contains short lengths of DNA (∼1,000 bp) in methylome reported the association between aberrant which CpG is commonly located (∼1 per 10 bp) in methylation and the abnormalities in the expression of critical unmethylated form and referred as CpG islands; they genes known to have critical roles during aging and neuro- commonly overlap with the transcription start sites (TSSs) of degenerative diseases. Consequently, the role of methylation genes. In human DNA, 5mC is present in approximately 1.5% in understanding neurodegenerative diseases has been under of the whole genome and CpG base pairs are 5-fold enriched focus. This review outlines the current knowledge of the human in CpG islands than other regions of the genome (3, 4). CpG brain DNA methylomes during aging and neurodegenerative islands have the following salient features. In the human diseases. -

Metabolic Network-Based Stratification of Hepatocellular Carcinoma Reveals Three Distinct Tumor Subtypes
Metabolic network-based stratification of hepatocellular carcinoma reveals three distinct tumor subtypes Gholamreza Bidkhoria,b,1, Rui Benfeitasa,1, Martina Klevstigc,d, Cheng Zhanga, Jens Nielsene, Mathias Uhlena, Jan Borenc,d, and Adil Mardinoglua,b,e,2 aScience for Life Laboratory, KTH Royal Institute of Technology, SE-17121 Stockholm, Sweden; bCentre for Host-Microbiome Interactions, Dental Institute, King’s College London, SE1 9RT London, United Kingdom; cDepartment of Molecular and Clinical Medicine, University of Gothenburg, SE-41345 Gothenburg, Sweden; dThe Wallenberg Laboratory, Sahlgrenska University Hospital, SE-41345 Gothenburg, Sweden; and eDepartment of Biology and Biological Engineering, Chalmers University of Technology, SE-41296 Gothenburg, Sweden Edited by Sang Yup Lee, Korea Advanced Institute of Science and Technology, Daejeon, Republic of Korea, and approved November 1, 2018 (received for review April 27, 2018) Hepatocellular carcinoma (HCC) is one of the most frequent forms of of markers associated with recurrence and poor prognosis (13–15). liver cancer, and effective treatment methods are limited due to Moreover, genome-scale metabolic models (GEMs), collections tumor heterogeneity. There is a great need for comprehensive of biochemical reactions, and associated enzymes and transporters approaches to stratify HCC patients, gain biological insights into have been successfully used to characterize the metabolism of subtypes, and ultimately identify effective therapeutic targets. We HCC, as well as identify drug targets for HCC patients (11, 16–18). stratified HCC patients and characterized each subtype using tran- For instance, HCC tumors have been stratified based on the uti- scriptomics data, genome-scale metabolic networks and network lization of acetate (11). Analysis of HCC metabolism has also led topology/controllability analysis. -

Regulation and Function of Silayltransferases in Pancreatic Cancer
REGULATION AND FUNCTION OF SILAYLTRANSFERASES IN PANCREATIC CANCER Sònia Bassagañas i Puigdemont Dipòsit legal: Gi. 240-2015 http://hdl.handle.net/10803/285783 ADVERTIMENT. L'accés als continguts d'aquesta tesi doctoral i la seva utilització ha de respectar els drets de la persona autora. Pot ser utilitzada per a consulta o estudi personal, així com en activitats o materials d'investigació i docència en els termes establerts a l'art. 32 del Text Refós de la Llei de Propietat Intel·lectual (RDL 1/1996). Per altres utilitzacions es requereix l'autorització prèvia i expressa de la persona autora. En qualsevol cas, en la utilització dels seus continguts caldrà indicar de forma clara el nom i cognoms de la persona autora i el títol de la tesi doctoral. No s'autoritza la seva reproducció o altres formes d'explotació efectuades amb finalitats de lucre ni la seva comunicació pública des d'un lloc aliè al servei TDX. Tampoc s'autoritza la presentació del seu contingut en una finestra o marc aliè a TDX (framing). Aquesta reserva de drets afecta tant als continguts de la tesi com als seus resums i índexs. ADVERTENCIA. El acceso a los contenidos de esta tesis doctoral y su utilización debe respetar los derechos de la persona autora. Puede ser utilizada para consulta o estudio personal, así como en actividades o materiales de investigación y docencia en los términos establecidos en el art. 32 del Texto Refundido de la Ley de Propiedad Intelectual (RDL 1/1996). Para otros usos se requiere la autorización previa y expresa de la persona autora. -

A Concise Review of Human Brain Methylome During Aging and Neurodegenerative Diseases
BMB Rep. 2019; 52(10): 577-588 BMB www.bmbreports.org Reports Invited Mini Review A concise review of human brain methylome during aging and neurodegenerative diseases Renuka Prasad G & Eek-hoon Jho* Department of Life Science, University of Seoul, Seoul 02504, Korea DNA methylation at CpG sites is an essential epigenetic mark position of carbon in the cytosine within CG dinucleotides that regulates gene expression during mammalian development with resultant formation of 5mC. The symmetrical CG and diseases. Methylome refers to the entire set of methylation dinucleotides are also called as CpG, due to the presence of modifications present in the whole genome. Over the last phosphodiester bond between cytosine and guanine. The several years, an increasing number of reports on brain DNA human genome contains short lengths of DNA (∼1,000 bp) in methylome reported the association between aberrant which CpG is commonly located (∼1 per 10 bp) in methylation and the abnormalities in the expression of critical unmethylated form and referred as CpG islands; they genes known to have critical roles during aging and neuro- commonly overlap with the transcription start sites (TSSs) of degenerative diseases. Consequently, the role of methylation genes. In human DNA, 5mC is present in approximately 1.5% in understanding neurodegenerative diseases has been under of the whole genome and CpG base pairs are 5-fold enriched focus. This review outlines the current knowledge of the human in CpG islands than other regions of the genome (3, 4). CpG brain DNA methylomes during aging and neurodegenerative islands have the following salient features. In the human diseases. -
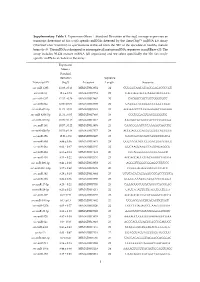
Supplementary Table 1. Expression
Supplementary Table 1. Expression (Mean Standard Deviation of the log2 average expression or transcript detection) of Sus scrofa specific miRNAs detected by the GeneChip™ miRNA 4.0 Array (ThermoFisher Scientific) in spermatozoa retrieved from the SRF of the ejaculate of healthy mature boars (n=3). The miRNA is designed to interrogate all mature miRNA sequences in miRBase v20. The array includes 30.424 mature miRNA (all organisms) and we select specifically the 326 Sus scrofa- specific miRNAs included in the array. Expression Mean ± Standard Deviation Sequence Transcript ID (log2) Accession Length Sequence ssc-miR-1285 13.98 ± 0.13 MIMAT0013954 24 CUGGGCAACAUAGCGAGACCCCGU ssc-miR-16 12.6 ± 0.74 MIMAT0007754 22 UAGCAGCACGUAAAUAUUGGCG ssc-miR-4332 12.32 ± 0.29 MIMAT0017962 20 CACGGCCGCCGCCGGGCGCC ssc-miR-92a 12.06 ± 0.09 MIMAT0013908 22 UAUUGCACUUGUCCCGGCCUGU ssc-miR-671-5p 11.73 ± 0.54 MIMAT0025381 24 AGGAAGCCCUGGAGGGGCUGGAGG ssc-miR-4334-5p 11.31 ± 0.05 MIMAT0017966 19 CCCUGGAGUGACGGGGGUG ssc-miR-425-5p 10.99 ± 0.15 MIMAT0013917 23 AAUGACACGAUCACUCCCGUUGA ssc-miR-191 10.57 ± 0.22 MIMAT0013876 23 CAACGGAAUCCCAAAAGCAGCUG ssc-miR-92b-5p 10.53 ± 0.18 MIMAT0017377 24 AGGGACGGGACGCGGUGCAGUGUU ssc-miR-15b 10.01 ± 0.9 MIMAT0002125 22 UAGCAGCACAUCAUGGUUUACA ssc-miR-30d 9.89 ± 0.36 MIMAT0013871 24 UGUAAACAUCCCCGACUGGAAGCU ssc-miR-26a 9.62 ± 0.47 MIMAT0002135 22 UUCAAGUAAUCCAGGAUAGGCU ssc-miR-484 9.55 ± 0.14 MIMAT0017974 20 CCCAGGGGGCGACCCAGGCU ssc-miR-103 9.53 ± 0.22 MIMAT0002154 23 AGCAGCAUUGUACAGGGCUAUGA ssc-miR-296-3p 9.41 ± 0.26 MIMAT0022958 -
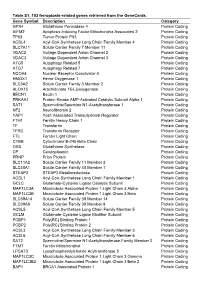
Table S1. 103 Ferroptosis-Related Genes Retrieved from the Genecards
Table S1. 103 ferroptosis-related genes retrieved from the GeneCards. Gene Symbol Description Category GPX4 Glutathione Peroxidase 4 Protein Coding AIFM2 Apoptosis Inducing Factor Mitochondria Associated 2 Protein Coding TP53 Tumor Protein P53 Protein Coding ACSL4 Acyl-CoA Synthetase Long Chain Family Member 4 Protein Coding SLC7A11 Solute Carrier Family 7 Member 11 Protein Coding VDAC2 Voltage Dependent Anion Channel 2 Protein Coding VDAC3 Voltage Dependent Anion Channel 3 Protein Coding ATG5 Autophagy Related 5 Protein Coding ATG7 Autophagy Related 7 Protein Coding NCOA4 Nuclear Receptor Coactivator 4 Protein Coding HMOX1 Heme Oxygenase 1 Protein Coding SLC3A2 Solute Carrier Family 3 Member 2 Protein Coding ALOX15 Arachidonate 15-Lipoxygenase Protein Coding BECN1 Beclin 1 Protein Coding PRKAA1 Protein Kinase AMP-Activated Catalytic Subunit Alpha 1 Protein Coding SAT1 Spermidine/Spermine N1-Acetyltransferase 1 Protein Coding NF2 Neurofibromin 2 Protein Coding YAP1 Yes1 Associated Transcriptional Regulator Protein Coding FTH1 Ferritin Heavy Chain 1 Protein Coding TF Transferrin Protein Coding TFRC Transferrin Receptor Protein Coding FTL Ferritin Light Chain Protein Coding CYBB Cytochrome B-245 Beta Chain Protein Coding GSS Glutathione Synthetase Protein Coding CP Ceruloplasmin Protein Coding PRNP Prion Protein Protein Coding SLC11A2 Solute Carrier Family 11 Member 2 Protein Coding SLC40A1 Solute Carrier Family 40 Member 1 Protein Coding STEAP3 STEAP3 Metalloreductase Protein Coding ACSL1 Acyl-CoA Synthetase Long Chain Family Member 1 Protein -

Reveals Deregulation of Central Metabolic Pathways in Hepatocellular Carcinoma
The Differential Rank Conservation Algorithm (DIRAC) Reveals Deregulation of Central Metabolic Pathways in Hepatocellular Carcinoma Master of Science Thesis Author: Elias Bj¨ornson contact: [email protected] Supervisor: Adil Mardinoglu Examiner: Jens Nielsen Systems & Synthetic Biology Department of Chemical and Biological Engineering Chalmers University of Technology Gothenburg, Sweden June 10, 2014 Contents 1 Goal and purpose 1 2 Thesis outline 1 3 Introduction 3 3.1 Hepatocellular carcinoma . 3 3.2 The Cancer Genome Atlas (TCGA) data base . 4 3.3 Gene set collections . 4 3.4 The DIRAC algorithm . 5 3.4.1 What does deregulation mean? . 8 3.4.2 Can deregulation reveal frequently mutated subnetworls? . 8 3.4.3 What does differential regulation mean? . 9 3.5 Reporter metabolites . 10 4 Results & Discussion 11 4.1 High-entropy networks in HCC . 11 4.1.1 TCA cycle . 17 4.1.2 Electron transport chain . 18 4.1.3 Fatty acid metabolism . 18 4.1.4 Carnitine shuttle and β-oxidation . 18 4.1.5 Glutamine and glutamate metabolism . 19 4.1.6 Altered energy metabolism in HCC . 19 4.1.7 Global deregulation . 21 4.2 Low-entropy networks in HCC . 22 4.2.1 Fatty acid biosynthesis . 25 4.2.2 Terpenoid biosynthesis . 27 4.2.3 ROS detoxification . 27 4.3 Differentially regulated networks in HCC . 28 4.3.1 Sphingolipid and glycosphingolipid metabolism . 31 4.4 Reporter metabolites . 33 4.5 Network entropy in other cancers . 35 4.6 Criticism . 38 5 Conclusions 38 6 Materials & Methods 40 6.1 Implementation of DIRAC . -

Regulatory T Cell Activation Triggers Specific Changes in Glycosylation
bioRxiv preprint doi: https://doi.org/10.1101/2020.07.29.226399; this version posted July 30, 2020. The copyright holder for this preprint (which was not certified by peer review) is the author/funder. All rights reserved. No reuse allowed without permission. 2 Regulatory T cell activation triggers specific changes in 3 glycosylation associated with Siglec-1-dependent inflammatory 4 responses 5 6 Gang Wu, Gavuthami Murugesan, Manjula Nagala, Alex McCraw, Stuart M. Haslam1, Anne Dell1, 7 Paul R. Crocker 8 9 Division of Cell Signalling and Immunology, School of Life Sciences, University of Dundee, Dundee, 10 DD1 5EH, Scotland, United Kingdom 11 1 Department of Life Sciences, Imperial College London, London, United Kingdom 12 13 14 Abstract 15 Siglec-1 is a macrophage lectin-like receptor that mediates sialic acid-dependent cellular interactions. 16 It was shown previously to promote inflammation in autoimmune disease through suppressing the 17 expansion of regulatory T cells (Tregs). We have investigated the molecular basis for Siglec-1 binding 18 to these cells using in vitro-induced Tregs. Siglec-1 binding was strongly upregulated on activated cells, 19 but lost under resting conditions. Glycosylation changes that affect Siglec-1 binding were studied by 20 comparing activated and resting Tregs using RNA-Seq, glycomics, proteomics and binding of selected 21 antibodies and lectins. A proximity labelling and proteomics strategy identified 49 glycoproteins 22 expressed by activated Tregs that may function as Siglec-1 counter-receptors. These represent ~5% 23 of the total membrane protein pool and were mainly related to T cell activation and proliferation. -

Sheet1 Page 1 Gene Symbol Gene Description Entrez Gene ID
Sheet1 RefSeq ID ProbeSets Gene Symbol Gene Description Entrez Gene ID Sequence annotation Seed matches location(s) Ago-2 binding specific enrichment (replicate 1) Ago-2 binding specific enrichment (replicate 2) OE lysate log2 fold change (replicate 1) OE lysate log2 fold change (replicate 2) Probability NM_022823 218843_at FNDC4 Homo sapiens fibronectin type III domain containing 4 (FNDC4), mRNA. 64838 TR(1..1649)CDS(367..1071) 1523..1530 3.73 1.77 -1.91 -0.39 1 NM_003919 204688_at SGCE Homo sapiens sarcoglycan, epsilon (SGCE), transcript variant 2, mRNA. 8910 TR(1..1709)CDS(112..1425) 1495..1501 3.09 1.56 -1.02 -0.27 1 NM_006982 206837_at ALX1 Homo sapiens ALX homeobox 1 (ALX1), mRNA. 8092 TR(1..1320)CDS(5..985) 916..923 2.99 1.93 -0.19 -0.33 1 NM_019024 233642_s_at HEATR5B Homo sapiens HEAT repeat containing 5B (HEATR5B), mRNA. 54497 TR(1..6792)CDS(97..6312) 5827..5834,4309..4315 3.28 1.51 -0.92 -0.23 1 NM_018366 223431_at CNO Homo sapiens cappuccino homolog (mouse) (CNO), mRNA. 55330 TR(1..1546)CDS(96..749) 1062..1069,925..932 2.89 1.51 -1.2 -0.41 1 NM_032436 226194_at C13orf8 Homo sapiens chromosome 13 open reading frame 8 (C13orf8), mRNA. 283489 TR(1..3782)CDS(283..2721) 1756..1762,3587..3594,1725..1731,3395..3402 2.75 1.72 -1.38 -0.34 1 NM_031450 221534_at C11orf68 Homo sapiens chromosome 11 open reading frame 68 (C11orf68), mRNA. 83638 TR(1..1568)CDS(153..908) 967..973 3.07 1.35 -0.72 -0.06 1 NM_033318 225795_at,225794_s_at C22orf32 Homo sapiens chromosome 22 open reading frame 32 (C22orf32), mRNA.