DOCSLIB.ORG

A Calibration of the 85 Peg Binary System

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
A Calibration of the 85 Peg Binary System A&A 392, 529–533 (2002) Astronomy DOI: 10.1051/0004-6361:20020962 & c ESO 2002 Astrophysics A calibration of the 85 Peg binary system J. Fernandes1,P.Morel2, and Y. Lebreton3 1 Observat´orio Astron´omico da Universidade de Coimbra, Santa Clara, 3040 Coimbra, Portugal and Departamento de Matem´atica da Faculdade de Ciˆencias e Tecnologia da Universidade de Coimbra, Portugal 2 D´epartement Cassini, UMR CNRS 6529, Observatoire de la Cˆote d’Azur, BP 4229, 06304 Nice Cedex 4, France 3 GEPI, Observatoire de Paris Meudon, 92195 Meudon, France Received 28 September 2001 / Accepted 11 June 2002 Abstract. We have calibrated the initial abundances, age and mixing-length parameters of the visual binary system 85 Pegasi. We obtain an age t85 Peg = 9 345 500 Myr, masses mA = 0:88 0:01 M and mB = 0:55 0:02 M , an initial helium mass = : : Fe = − : : Λ = : : fraction Yi 0 25 0 01, an initial metallicity [ H ]i 0 185 0 054 and mixing-length parameters A 1 80 0 05 and ΛB = 2:14 0:10. We find that, as already proposed, 85 Peg B is itself a binary. The mass of the unseen companion is mb ≈ 0:11 M . Key words. stars: binaries: visual – stars: evolution – stars: fundamental parameters – stars: individual: 85 Peg 1. Introduction massive than 85 Peg A the brighter one (e.g. Slocum 1915; Hall 1948; Underhill 1963). This was found again by Martin & The calibration of a binary system is based on the adjustment Fe Mignard (1998) on the basis of Hipparcos observations. This of stellar modeling parameters (t?; Y ; [ ] ; Λ ; Λ ) to the ob- i H i A B abnormal situation could be explained by the fact that 85 Peg B servational data at the age t? of the system, with the reasonable is an undetected binary. 85 Peg A is known as a metal-poor star hypothesis of a common origin for both components (same ini- and found to be much older than the Sun (Perrin et al. 1977). tial chemical composition and age). Y and [ Fe ] are, respec- i H i Because of its small mass, 85 Peg A sits close to the zams Λ tively, the initial helium mass fraction and metallicity, A and which gives a constraint on its initial helium abundance, a Λ B are respectively the mixing-length parameters of the pri- value traditionally associated with primordial helium (Perrin mary A and secondary B. For each component one also infers et al. 1977; Catchpole et al. 1967; Smak 1960). a mass value consistent with theoretical stellar modeling. The photometry and the atmospheric parameters of Taking into account the most recent theoretical and 85 Peg A have been determined many times. The first spectro- observational astrometric, spectroscopic and photometric scopic determination of the metallicity is from Wallerstein & results we undertake the calibration of 85 Pegasi (HD 224930, Helfer (1959), while the most recent metallicity and effective HIP 171, BD+26 4734 4, HR 9088, β 733 ADS 17175, temperature determinations are due to van’t Veer (2000) and IDS 23569 +2633; α = 00h 02m 10s, δ =+27◦0405600 (2000)). Fulbright (2000). While 85 Peg A is a well known star, the sec- It is a well-known visual and single-lined spectroscopic binary ondary component is less well known. The greatest limitations system. The components, 85 Peg A and B, are main sequence to studying 85 Peg B in detail were the lack of individual photo- low mass stars of spectral types G5 and K7 respectively metric and spectroscopic measurements due to its proximity to (ten Brummelaar et al. 2000). The shortness of the period 85 Peg A (ρ ≈ 000: 75). Recently, ten Brummelaar et al. (2000), (≈27 years) and the proximity to the Sun (∼12 pc) give it an in- performed differential photometry in the Johnson vri system teresting place among the binary stars. The visual orbit is very for both stars using adaptative optics, which allows us to deter- well known (Hall 1948). Nevertheless, some studies of the or- mine the effective temperatures and bolometric magnitudes of bit have been recently published. The latest (S¨oderhjelm 1999) both components. has yielded improvements to the Hipparcos trigonometric parallax and orbit, combining data from the satellite with In their pioneering work Fernandes et al. (1998) tried to ground-based observations. 85 Peg is one of the rare cases calibrate the helium abundance and age of both 85 Peg A and for which the mass ratio can be obtained by both astrometric B by means of stellar models. No solution was possible when and spectroscopic observations. For many years investigators fitting both components for the same helium and age values. have claimed that 85 Peg B, the fainter component, is more The models appeared to be hotter than the observations. The discrepancy appears to be removed if the microscopic diffusion Send offprint requests to: J. Fernandes, of helium and heavy elements, the enrichment of α-elements e-mail: [email protected] and the non-lte effects in the iron abundances determinations Article published by EDP Sciences and available at http://www.aanda.org or http://dx.doi.org/10.1051/0004-6361:20020962 530 J. Fernandes et al.: Improved calibration of 85 Peg Table 1. Relevant orbital elements of the 85 Peg. As usual P is the orbital period in years, a the semi-major axis, i the inclination and e the eccentricity. The error bars are probable errors. S¨oderhjelm does not give the errors on the orbital elements but he indicates that the number of given decimals reflect the mean errors. Author Paie Hall (1948) 26:27 0:19 000: 83 000: 02 −50◦:0 2◦:00:38 0:01 S¨oderhjelm (1999) 26:28 000: 83 −49◦: 0:38 are taken into account in models of low mass stars (Lebreton the adopted orbital elements and parallax, we derive the “spec- et al. 1999). Nevertheless, Lebreton et al. did not perform a troscopic” mass fraction: full calibration of 85 Peg A and did not examine the secondary B = 0:43 0:06: component. s Our purpose here is (1) to provide a complete modeling of Note the remarkable agreement between spectroscopic and the system based on more appropriate stellar models (i.e. in- photographic determinations of the mass fraction. A weighted cluding microscopic diffusion) and (2) to propose a calibration average of the photographic and spectroscopic values leads to: of the unknown parameters (age, helium, individual masses) B85 Peg = 0:44 0:02: that fulfills the recent observational constraints. The paper is divided as follows. In Sect. 2, we collect and With the sum of masses and mass fraction derived above, the discuss the observational constraints. Section 3 is devoted to masses of the components are respectively: the description of physics and modeling. We summarize and mA = 0:84 0:08 M ; mB = 0:66 0:07 M ; conclude in Sect. 4. showing 85 Peg A definitively to be the more massive star. 2. Observations of the visual binary 85 Peg 2.2. Spectroscopic and photometric data 2.1. Astrometric data Stellar parameters were determined from spectroscopic and photometric analysis. Table 2 lists recently published data for For 85 Peg we are in the fortunate position of having two the photometry, effective temperature and metallicity of 85 Peg. precise, self consistent and independent determinations of the For 85 Peg A we chose to retain the recent determinations trigonometrical parallax and improved orbital elements; from Fe = − : ff = [ H ] 0 69 dex and Te A 5550 K of van’t Veer (2000). these data individual masses mA and mB can be derived inde- A This T ff determination relies on the careful fit of Balmer pendently. Table 1 shows the excellent agreement of the rel- e line profiles with Kurucz’s (1991) atlas model atmospheres evant elements of the astrometric orbits of Hall (1948) and with the constraint that the model reproduces both the Hα S¨oderhjelm (1999). The first determination of the parallax is and Hβ profiles. Furthermore we point out that, according to the standard photographic parallax (Wyller 1956; Heintz 1993) Th´evenin & Idiart (1999), the metallicity of metal-poor stars, based on improved orbit and several decades of photographic computed using model atmospheres in the lte approxima- long focus observations: the absolute photographic parallax 00 00 tion is underestimated by about 0.12 dex at the metallicity of amounts to $ = 0: 0798 0: 0033 (Heintz 1993). The abs 85 Peg. This is particularly important for the stellar position second determination is the recently improved adjustment of on the hr diagram (Lebreton et al. 1999). We take into ac- parallax and orbital elements by S¨oderhjelm (1999) based count this correction and adopt the value [ Fe ] = −0:57 0:11 on the Hipparcos 3.25 yr data and old ground-based observa- H A 00 00 (Th´evenin 2001). The α-elements (Mg, Ca, Si, Na, Al, Ti) tions yielding $ = 0: 0825 0: 0008. With the orbit of abs have been found to be enriched with respect to the Sun in Hall (1948) and the parallax of Heintz (1993) we derive the 85 Peg A (Fuhrmann 1998; van’t Veer 2000; Fulbright 2000). In sum of masses S = 1:63 0:33 M .Usingthedatafrom 85 Peg our calculations we take account of an α-elements enrichment, S¨oderhjelm (1999) we obtain S = 1:49 0:09 M .Forthe 85 Peg [α/Fe] =+0:40 dex, through appropriate opacities and input sum of masses we adopt the weighted average value: mixture. We computed the effective temperature of 85 Peg B Fe using the calibrations Teff = Teff {color; [ ]} from Lejeune S85 Peg = 1:50 0:09 M : H et al.
Load more

Recommended publications
  • Astronomie in Theorie Und Praxis 8. Auflage in Zwei Bänden Erik Wischnewski
    Astronomie in Theorie und Praxis 8. Auflage in zwei Bänden Erik Wischnewski Inhaltsverzeichnis 1 Beobachtungen mit bloßem Auge 37 Motivation 37 Hilfsmittel 38 Drehbare Sternkarte Bücher und Atlanten Kataloge Planetariumssoftware Elektronischer Almanach Sternkarten 39 2 Atmosphäre der Erde 49 Aufbau 49 Atmosphärische Fenster 51 Warum der Himmel blau ist? 52 Extinktion 52 Extinktionsgleichung Photometrie Refraktion 55 Szintillationsrauschen 56 Angaben zur Beobachtung 57 Durchsicht Himmelshelligkeit Luftunruhe Beispiel einer Notiz Taupunkt 59 Solar-terrestrische Beziehungen 60 Klassifizierung der Flares Korrelation zur Fleckenrelativzahl Luftleuchten 62 Polarlichter 63 Nachtleuchtende Wolken 64 Haloerscheinungen 67 Formen Häufigkeit Beobachtung Photographie Grüner Strahl 69 Zodiakallicht 71 Dämmerung 72 Definition Purpurlicht Gegendämmerung Venusgürtel Erdschattenbogen 3 Optische Teleskope 75 Fernrohrtypen 76 Refraktoren Reflektoren Fokus Optische Fehler 82 Farbfehler Kugelgestaltsfehler Bildfeldwölbung Koma Astigmatismus Verzeichnung Bildverzerrungen Helligkeitsinhomogenität Objektive 86 Linsenobjektive Spiegelobjektive Vergütung Optische Qualitätsprüfung RC-Wert RGB-Chromasietest Okulare 97 Zusatzoptiken 100 Barlow-Linse Shapley-Linse Flattener Spezialokulare Spektroskopie Herschel-Prisma Fabry-Pérot-Interferometer Vergrößerung 103 Welche Vergrößerung ist die Beste? Blickfeld 105 Lichtstärke 106 Kontrast Dämmerungszahl Auflösungsvermögen 108 Strehl-Zahl Luftunruhe (Seeing) 112 Tubusseeing Kuppelseeing Gebäudeseeing Montierungen 113 Nachführfehler
    [Show full text]
  • UNSC Science and Technology Command
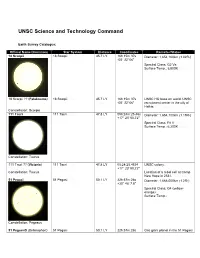
    UNSC Science and Technology Command Earth Survey Catalogue: Official Name/(Common) Star System Distance Coordinates Remarks/Status 18 Scorpii {TCP:p351} 18 Scorpii {Fact} 45.7 LY 16h 15m 37s Diameter: 1,654,100km (1.02R*) {Fact} -08° 22' 06" {Fact} Spectral Class: G2 Va {Fact} Surface Temp.: 5,800K {Fact} 18 Scorpii ?? (Falaknuma) 18 Scorpii {Fact} 45.7 LY 16h 15m 37s UNSC HQ base on world. UNSC {TCP:p351} {Fact} -08° 22' 06" recruitment center in the city of Halkia. {TCP:p355} Constellation: Scorpio 111 Tauri 111 Tauri {Fact} 47.8 LY 05h:24m:25.46s Diameter: 1,654,100km (1.19R*) {Fact} +17° 23' 00.72" {Fact} Spectral Class: F8 V {Fact} Surface Temp.: 6,200K {Fact} Constellation: Taurus 111 Tauri ?? (Victoria) 111 Tauri {Fact} 47.8 LY 05:24:25.4634 UNSC colony. {GoO:p31} {Fact} +17° 23' 00.72" Constellation: Taurus Location of a rebel cell at Camp New Hope in 2531. {GoO:p31} 51 Pegasi {Fact} 51 Pegasi {Fact} 50.1 LY 22h:57m:28s Diameter: 1,668,000km (1.2R*) {Fact} +20° 46' 7.8" {Fact} Spectral Class: G4 (yellow- orange) {Fact} Surface Temp.: Constellation: Pegasus 51 Pegasi-B (Bellerophon) 51 Pegasi 50.1 LY 22h:57m:28s Gas giant planet in the 51 Pegasi {Fact} +20° 46' 7.8" system informally named Bellerophon. Diameter: 196,000km. {Fact} Located on the edge of UNSC territory. {GoO:p15} Its moon, Pegasi Delta, contained a Covenant deuterium/tritium refinery destroyed by covert UNSC forces in 2545. {GoO:p13} Constellation: Pegasus 51 Pegasi-B-1 (Pegasi 51 Pegasi 50.1 LY 22h:57m:28s Moon of the gas giant planet 51 Delta) {GoO:p13} +20° 46' 7.8" Pegasi-B in the 51 Pegasi star Constellation: Pegasus system; a Covenant stronghold on the edge of UNSC territory.
    [Show full text]
  • Curriculum Vitae Date: 4/03/2013 Initials
    Curriculum Vitae Date: 4/03/2013 Initials: Gordon Arthur Hunter WALKER Born: 30 January 1936 Married: Sigrid Helene Fischer, April 1962 Children: Nicholas and Eric Languages: English, French, and German. POST-SECONDARY EDUCATION University of Edinburgh Hon.B.Sc. Natural Philosophy 1958 University of Cambridge (Caius) Ph.D. Astrophysics 1962 PROFESSIONAL EMPLOYMENT Radcliffe Observatory, Pretoria Research Assistant 1960-61 DAO, Victoria NRC Fellow 1962-63 DAO, Victoria Scientific Officer 3 1963-69 University of Texas Visiting Lecturer 1965 (Spring) University of Victoria Visiting Lecturer 1966 (Spring) UBC Associate Professor April 1, 1969 Director, Institute 1972-78 Astronomy and Space Science Professor July 1, 1974-97 Professor Emeritus July 1 1997 { HIA/NRC Guest-worker 1998 { UVic Adjunct Professor April 23 2004 { INTERNATIONAL PROJECTS Scientific Advisory Committee of the CFHT 1972-79 Project Scientist for `Starlab' an Australian, Canadian, NASA, space telescope proposal until Canada withdrew in 1984 CFHT Board of Directors 1986-91 Canadian Project Scientist (1989-90): EUVITA - far ultraviolet astronomical satellite experiment joint with USSR, Switzerland, USA. Canadian Project Scientist (1990{97): Gemini - twin 8 metre optical telescopes (1 in Hawaii, 1 in Chile) joint with USA, U.K., Chile, Australia, Argentina, Brazil. Gemini Scientific Advisory Committee 1991{97 Gemini Board of Directors 1991{97 1 MOST Science team (1997{2009): a Canadian satellite launched in 2003 for ultra-precise photom- etry of bright stars, with collaboration from Austria. Gemini/NSF Visiting Committee 2004 AURA Source Selection Board for future Gemini Instrumentation 2004 TMT - chair HROS Review Panel 2005 chair Gemini Source Selection Board for HRNIRS 2005 chair Gemini Source Selection Board for PRVS 2006 member SPIRou Preliminary Design Revue Committee 2012 - a high resolution visible/infrared spectropolarimeter proposed for CFHT RESEARCH CAREER My fascination with astronomy began at age 7 when my father explained that stars were very distant suns.
    [Show full text]
  • Numbers 1 to 100
    Numbers 1 to 100 PDF generated using the open source mwlib toolkit. See http://code.pediapress.com/ for more information. PDF generated at: Tue, 30 Nov 2010 02:36:24 UTC Contents Articles −1 (number) 1 0 (number) 3 1 (number) 12 2 (number) 17 3 (number) 23 4 (number) 32 5 (number) 42 6 (number) 50 7 (number) 58 8 (number) 73 9 (number) 77 10 (number) 82 11 (number) 88 12 (number) 94 13 (number) 102 14 (number) 107 15 (number) 111 16 (number) 114 17 (number) 118 18 (number) 124 19 (number) 127 20 (number) 132 21 (number) 136 22 (number) 140 23 (number) 144 24 (number) 148 25 (number) 152 26 (number) 155 27 (number) 158 28 (number) 162 29 (number) 165 30 (number) 168 31 (number) 172 32 (number) 175 33 (number) 179 34 (number) 182 35 (number) 185 36 (number) 188 37 (number) 191 38 (number) 193 39 (number) 196 40 (number) 199 41 (number) 204 42 (number) 207 43 (number) 214 44 (number) 217 45 (number) 220 46 (number) 222 47 (number) 225 48 (number) 229 49 (number) 232 50 (number) 235 51 (number) 238 52 (number) 241 53 (number) 243 54 (number) 246 55 (number) 248 56 (number) 251 57 (number) 255 58 (number) 258 59 (number) 260 60 (number) 263 61 (number) 267 62 (number) 270 63 (number) 272 64 (number) 274 66 (number) 277 67 (number) 280 68 (number) 282 69 (number) 284 70 (number) 286 71 (number) 289 72 (number) 292 73 (number) 296 74 (number) 298 75 (number) 301 77 (number) 302 78 (number) 305 79 (number) 307 80 (number) 309 81 (number) 311 82 (number) 313 83 (number) 315 84 (number) 318 85 (number) 320 86 (number) 323 87 (number) 326 88 (number)
    [Show full text]
  • Theory of Stellar Atmospheres
    © Copyright, Princeton University Press. No part of this book may be distributed, posted, or reproduced in any form by digital or mechanical means without prior written permission of the publisher. EXTENDED BIBLIOGRAPHY References [1] D. Abbott. The terminal velocities of stellar winds from early{type stars. Astrophys. J., 225, 893, 1978. [2] D. Abbott. The theory of radiatively driven stellar winds. I. A physical interpretation. Astrophys. J., 242, 1183, 1980. [3] D. Abbott. The theory of radiatively driven stellar winds. II. The line acceleration. Astrophys. J., 259, 282, 1982. [4] D. Abbott. The theory of radiation driven stellar winds and the Wolf{ Rayet phenomenon. In de Loore and Willis [938], page 185. Astrophys. J., 259, 282, 1982. [5] D. Abbott. Current problems of line formation in early{type stars. In Beckman and Crivellari [358], page 279. [6] D. Abbott and P. Conti. Wolf{Rayet stars. Ann. Rev. Astr. Astrophys., 25, 113, 1987. [7] D. Abbott and D. Hummer. Photospheres of hot stars. I. Wind blan- keted model atmospheres. Astrophys. J., 294, 286, 1985. [8] D. Abbott and L. Lucy. Multiline transfer and the dynamics of stellar winds. Astrophys. J., 288, 679, 1985. [9] D. Abbott, C. Telesco, and S. Wolff. 2 to 20 micron observations of mass loss from early{type stars. Astrophys. J., 279, 225, 1984. [10] C. Abia, B. Rebolo, J. Beckman, and L. Crivellari. Abundances of light metals and N I in a sample of disc stars. Astr. Astrophys., 206, 100, 1988. [11] M. Abramowitz and I. Stegun. Handbook of Mathematical Functions. (Washington, DC: U.S. Government Printing Office), 1972.
    [Show full text]
  • The Project Gutenberg Ebook #26147: Publications of The
    The Project Gutenberg EBook of Publications of the Astronomical Society of the Pacific, by Various This eBook is for the use of anyone anywhere at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this eBook or online at www.gutenberg.org Title: Publications of the Astronomical Society of the Pacific Volume 1 Author: Various Release Date: July 29, 2008 [EBook #26147] Language: English Character set encoding: ISO-8859-1 *** START OF THIS PROJECT GUTENBERG EBOOK ASTRONOMICAL SOCIETY OF THE PACIFIC *** PUBLICATIONS o f t h e ASTRONOMICAL SOCIETY OF THE PACIFIC. (Founded February 7, 1889.) V O L U M E I. 1889. SAN FRANCISCO: printed for the society. 1889. Produced by Susan Skinner, Nigel Blower, Jonathan Niehof and the Online Distributed Proofreading Team at http://www.pgdp.net Transcriber’s notes: the following corrigenda provided in the original volume have been im- plemented in this text. Other minor corrections are detailed in the source code. CORRIGENDA. Page 39; Insert a star (*) to signify life-membership after the following names, viz: Charles Goodall, Horace L. Hill, D. O. Mills. Page 44; for 5 × 7 read 4 × 5. Page 59; Column “Star”; for W. H. Z. read W. M. Z. Page 71; add to Mr. Boulton’s address, (Box 2015, New York City). Page 71; for Centreville read Warm Springs. Page 71; for Terry read Torrey. TABLEOFCONTENTS. Publications No. 1. (February 7, 1889). List of Officers pro tem. .................................... 1 Circular .
    [Show full text]
  • Title on the Rotation of Celestial Bodies Author(S) Shinjo, Shinzo
    Title On the Rotation of Celestial Bodies Author(s) Shinjo, Shinzo; Watanabe, Yoshikatsu Memoirs of the College of Science, Kyoto Imperial University Citation (1918), 3(7): 199-222 Issue Date 1918-08-15 URL http://hdl.handle.net/2433/256513 Right Type Departmental Bulletin Paper Textversion publisher Kyoto University On the Rotation of Celestial Bodies. BY Shinzo Shinjo and Yoshik.atsu Watanabe. (Received May 27, 1918.) Although the rotation of celestial bodies or of celestial systems has hitherto very often been discussed, the amount of their angular momenta, strange to say, has not so far been made the subject of thorough investigation, except in the case of our solar system. The main cause of this may of course lie in the fact that good reliable parallaxes have always been rare. Since, as is well known, the an­ gular momentum of an isolated body or of an isolated system must remain forever constant, any knowledge of its amo~nt will always prove t<;> be a valuable and important data for the discussion of the evolution of such a body or system. Three years ago we calculated the masses ~nd angular momenta of certain binary systems-I I visual binaries with known parallaxes, and 8 eclipsing spectroscopic binaries-and found the remarkable fact that not only the masses but also the angular momenta of these binary systems, were of about the same order of magnitude, the latter being indeed several hundred times greater than that of our solar system. Upon this· fact we built our theory of the cause of the rotation of celestial bodies ; and showed that the observed fact could be weU accounted for, if we assumed the binary systems to have been built up of a large multitude of meteorites, each about the size of the asteroids in our solar system.
    [Show full text]
  • Annual Report 2009 ESO
    ESO European Organisation for Astronomical Research in the Southern Hemisphere Annual Report 2009 ESO European Organisation for Astronomical Research in the Southern Hemisphere Annual Report 2009 presented to the Council by the Director General Prof. Tim de Zeeuw The European Southern Observatory ESO, the European Southern Observa­ tory, is the foremost intergovernmental astronomy organisation in Europe. It is supported by 14 countries: Austria, Belgium, the Czech Republic, Denmark, France, Finland, Germany, Italy, the Netherlands, Portugal, Spain, Sweden, Switzerland and the United Kingdom. Several other countries have expressed an interest in membership. Created in 1962, ESO carries out an am­ bitious programme focused on the de­ sign, construction and operation of power­ ful ground­based observing facilities enabling astronomers to make important scientific discoveries. ESO also plays a leading role in promoting and organising cooperation in astronomical research. ESO operates three unique world­ View of the La Silla Observatory from the site of the One of the most exciting features of the class observing sites in the Atacama 3.6 ­metre telescope, which ESO operates together VLT is the option to use it as a giant opti­ with the New Technology Telescope, and the MPG/ Desert region of Chile: La Silla, Paranal ESO 2.2­metre Telescope. La Silla also hosts national cal interferometer (VLT Interferometer or and Chajnantor. ESO’s first site is at telescopes, such as the Swiss 1.2­metre Leonhard VLTI). This is done by combining the light La Silla, a 2400 m high mountain 600 km Euler Telescope and the Danish 1.54­metre Teles cope.
    [Show full text]
  • Ghosts of Onyx
    Scanned and formatted by Galmarman. Color: White • Off-White • Light Grey • Silver • Beige • Wheat • Burlywood • Tan • Black Text Size: 10 • 11 • 12 • 12.5 • 13 • 13.5 • 14 • 14.5 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 GHOSTS OF ONYX ERIC NYLUND A TOM DOHERTY ASSOCIATES BOOK NEW YORK This is a work of fiction. All the characters and events portrayed in this novel are either fictitious or are used fictitiously. HALO®: GHOSTS OF ONYX Copyright © 2006 by the Microsoft Corporation All rights reserved, including the right to reproduce this book, or portions thereof, in any form. Microsoft, the Microsoft Game Studios Logo, Bungie, the Bungie Logo, Halo, the Halo Logo, Xbox, and the Xbox logos are either registered trademarks or trademarks of Microsoft Corporation in the United States and/or other countries that are used under license from owner. A Tor Book Published by Tom Doherty Associates, LLC 175 Fifth Avenue New York, NY 10010 www.tor.com Tor® is a registered trademark of Tom Doherty Associates, LLC. ISBN-13: 978-0-765-31568-7 ISBN-10: 0-765-31568-8 First Edition: November 2006 Printed in the United States of America 0987654321 For Halo fans everywhere Table of Contents: Acknowledgements Prologue Chapter 1 Chapter 2 Chapter 3 Chapter 4 Chapter 5 Chapter 6 Chapter 7 Chapter 8 Chapter 9 Chapter 10 Chapter 11 Chapter 12 Chapter 13 Chapter 14 Chapter 15 Chapter 16 Chapter 17 Chapter 18 Chapter 19 Chapter 20 Chapter 21 Chapter 22 Chapter 23 Chapter 24 Chapter 25 Chapter 26 Chapter 27 Chapter 28 Chapter 29 Chapter 30 Chapter 31 Chapter 32 Chapter 33 Chapter 34 Chapter 35 Chapter 36 Chapter 37 Chapter 38 Chapter 39 Chapter 40 Chapter 41 About the Author ^ → ACKNOWLEDGMENTS First and foremost my wife and fellow writer, Syne Mitchell, and my son, Kai.
    [Show full text]
  • Analysis of Angular Momentum in Planetary Systems and Host Stars
    Analysis of Angular Momentum in Planetary Systems and Host Stars by Stacy Ann Irwin Bachelor of Science, Computer Science University of Houston 2000 Master of Science, Space Sciences Florida Institute of Technology 2009 A dissertation submitted to the College of Science at Florida Institute of Technology in partial fulfillment of the requirements for the degree of Doctor of Philosophy in Space Sciences Melbourne, Florida July 2015 c Copyright 2015 Stacy Ann Irwin All Rights Reserved The author grants permission to make single copies We the undersigned committee hereby recommend that the attached document be accepted as fulfilling in part the requirements for the degree of Doctor of Philosophy in Space Sciences. \Analysis of Angular Momentum in Planetary Systems and Host Stars," a dissertation by Stacy Ann Irwin Samuel T. Durrance, Ph.D. Professor, Physics and Space Sciences Major Advisor Daniel Batcheldor, Ph.D. Associate Professor, Physics and Space Sciences Committee Member Darin Ragozzine, Ph.D. Assistant Professor, Physics and Space Sciences Committee Member Semen Koksal, Ph.D. Professor, Mathematical Sciences Outside Committee Member Daniel Batcheldor, Ph.D. Professor, Physics and Space Sciences Department Head Abstract Analysis of Angular Momentum in Planetary Systems and Host Stars by Stacy Ann Irwin Dissertation Advisor: Samuel T. Durrance, Ph.D. The spin angular momentum of single Main Sequence stars has long been shown to follow a primary power law of stellar mass, J M α, excluding stars of <2 solar masses. Lower mass / stars rotate more slowly with and have smaller moments of inertia, and as a result they contain much less spin angular momentum.
    [Show full text]
  • BRYCE CROLL September 14Th, 2016 800 King Street West, Apt
    BRYCE CROLL September 14th, 2016 800 King Street West, Apt. 402 Tel: (617) 358-4062 Toronto, Ontario, Canada [email protected] M5V 3M7 space.mit.edu/home/croll/ RESEARCH INTERESTS: - Near-infrared observations from the ground. - Extrasolar planets. - Ultra-cool dwarf variability. - Stellar spot modelling. EMPLOYMENT: Senior Postdoctoral Associate, Boston University, Boston, MA. (March 2015 – August 2016). Sagan Postdoctoral Fellow, Massachusetts Institute of Technology, Cambridge, MA. (September 2011 – August 2014). EDUCATION: Ph.D. 2011, University of Toronto (UofT), Astronomy & Astrophysics. Toronto, ON. Supervisors: Professors Dr. Norman Murray & Dr. Ray Jayawardhana Thesis Title: Near-infrared Characterization of the Atmospheres of Alien Worlds. B.Sc. 2006, University of British Columbia (UBC), Honours Physics. Vancouver, B.C. REFEREED PUBLICATIONS: (27 total publications, 856 citations, h-index of 15) (14 first author papers, 460 first author citations, first author h-index of 11) 27. Croll, B. et al. (2016) “Long-term, Multiwavelength Light Curves of Ultra-Cool Dwarfs: II. The evolving Light Curves of the T2.5 SIMP 0136 & the Uncorrelated Light Curves of the M9 TVLM 513.” Monthly Notices of the Royal Astronomical Society, submitted 2016 September 6th, astro- ph/1609.03587, NASA/ADS link. 26. Croll, B. et al. (2016) “Long-term, Multiwavelength Light Curves of Ultra-cool Dwarfs: I. An Interplay of Starspots & Clouds Likely Drive the Variability of the L3.5 dwarf 2MASS 0036+18.” Monthly Notices of the Royal Astronomical Society, submitted 2016 September 6th,, astro-ph/1609.03586, NASA/ADS link. 25. Rappaport, S., Gary, B., Kaye, T., Vanderburg, A., Croll, B., Benni, P. & Foote, J. (2016) “Drifting Asteroid Fragments around WD 1145+017.” Monthly Notices of the Royal Astronomical Society, 458, 3904, NASA/ADS link.
    [Show full text]
  • Exoplanet Science in a Solar System Context
    ( ! $ * )+'# $ # " %$$ !) $ ! &010./2 IAG/USP XVIII GMT Science and Instrumentation ASz 26 Feb 2018 Talk Outline • Exoplanet science in a historical context • Exoplanet science today • Solar System context • Exoplanet science today, in a little more detail • Orbital resonance • Intro to planet formation Exoplanet: A planet orbiting a star other than the Sun Planet: Less massive than a star, more massive than a planetesimal. • No internal nuclear burning, ever (but may be self- luminous from gravitational contraction). • Shaped by gravity (spherical) rather than agglutination. • Formed in protoplanetary disk. IAG/USP XVIII GMT Science and Instrumentation ASz 26 Feb 2018 Exoplanet Science- A Historical Context IAG/USP XVIII GMT Science and Instrumentation ASz 26 Feb 2018 Paleohistory of Exoplanet Science: • Giordano Bruno (1584) speculates on the “This space we declare to be infinite... In it are an infinity of worlds of the same kind as our inevitability that Earth-like exoplanets must own.” exist. - De l'infinito universo et mondi (1584) • Newton (1713) asserts that exo-solar "And if the fixed stars are the centres of similar systems, they will all be constructed according systems will not only harbor exo-Earths, but to a similar design and subject to the dominion will be identical to the Solar System. of One.".” - Principia, 2nd Edition (1713) • Struve (1952) argues that there is no reason “But there seems to be no compelling reason exoplanets should not be much closer to a why hypothetical stellar planets should not, in host star than Mercury is to the Sun. some instances, be closer to their parent stars than is the case in the solar system [sic].” The Observatory, 72, 1952 • Further proposes that super-Jupiters in close orbits should be detectable by Doppler spectroscopy of host star and forground extinction during transits.
    [Show full text]