DOCSLIB.ORG

Myosin-I by the PNAS PLUS N-Terminal Region

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Myosin-I by the PNAS PLUS N-Terminal Region Mechanochemical tuning of myosin-I by the PNAS PLUS N-terminal region Michael J. Greenberg, Tianming Lin, Henry Shuman, and E. Michael Ostap1 Pennsylvania Muscle Institute and the Department of Physiology, Perelman School of Medicine at the University of Pennsylvania, Philadelphia, PA 19104 Edited by James A. Spudich, Stanford University School of Medicine, Stanford, CA, and approved May 13, 2015 (received for review April 3, 2015) Myosins are molecular motors that generate force to power a wide only do these myosins have different responses to force, but also array of motile cellular functions. Myosins have the inherent ability they have different biochemical transitions that are affected by to change their ATPase kinetics and force-generating properties force (i.e., the rate of ADP release for Myo1b and the rate of ATP- when they encounter mechanical loads; however, little is known induced actomyosin detachment for Myo1c). about the structural elements in myosin responsible for force The high-resolution crystal structures of nucleotide-free sensing. Recent structural and biophysical studies have shown that Myo1b (i.e., rigor-like state) (4) and ADP.vanadate-bound Myo1c myosin-I isoforms, Myosin-Ib (Myo1b) and Myosin-Ic (Myo1c), have (i.e., pre–power-stroke state) (8) have recently been determined. similar unloaded kinetics and sequences but substantially different Despite being in different conformational states, these structures responses to forces that resist their working strokes. Myo1b has the show that Myo1b and Myo1c have a high degree of structural properties of a tension-sensing anchor, slowing its actin-detachment homology to each other and to other myosins (4, 16). A prominent kinetics by two orders of magnitude with just 1 pN of resisting feature in the Myo1b structure is the positioning of the N-terminal force, whereas Myo1c has the properties of a slow transporter, region (NTR), which is in a conformation that has not been ob- generating power without slowing under 1-pN loads that would served in other myosin structures (Fig. 1A). In myosin-II, -V, and stall Myo1b. To examine the structural elements that lead to differ- -VI the NTR includes an SH3-like domain that lies to the side of ences in force sensing, we used single-molecule and ensemble ki- the motor domain (17–19). In contrast, the Myo1b NTR sits in a netic techniques to show that the myosin-I N-terminal region (NTR) hydrophobic pocket between the motor and the lever arm helix plays a critical role in tuning myosin-I mechanochemistry. We found (LAH) and interacts with the first calmodulin light chain. As such, that replacing the Myo1c NTR with the Myo1b NTR changes the it is in a position that might enable it to communicate the position identity of the primary force-sensitive transition of Myo1c, resulting of the LAH to the nucleotide-binding site (4). Although the motor in sensitivity to forces of <2 pN. Additionally, we found that the – domain sequences of myosin-I isoforms are highly conserved, in- NTR plays an important role in stabilizing the post power-stroke cluding the residues that create the hydrophobic pocket in which conformation. These results identify the NTR as an important struc- the NTR sits, the NTR sequences are not conserved (Fig. 1B). We tural element in myosin force sensing and suggest a mechanism for hypothesized that the NTR plays a role in establishing kinetic generating diversity of function among myosin isoforms. diversity among myosins (4). To investigate whether the NTR of Myo1c plays a role in mechanochemistry | optical tweezers | mechanosensing | mechanosensing, we expressed Myo1c constructs with the native transient kinetics | single molecule NTR present, with the NTR deleted, and with the Myo1b NTR in place of the native sequence and measured their kinetic and me- yosin motors use the energy from ATP hydrolysis to power chanical properties in the presence and absence of force. We find Ma wide array of cellular processes including muscle con- that the NTR of Myo1c plays important roles in tuning Myo1c’s traction, cell migration, membrane trafficking, cell division, and kinetics in the presence and absence of load and in stabilizing the intracellular transport (for review, see ref. 1). To optimally function in such diverse processes, different myosin isoforms BIOPHYSICS AND Significance have evolved distinct kinetic and mechanical properties to meet COMPUTATIONAL BIOLOGY their physiological demands (for review, see ref. 2), including differing abilities to adapt their ATPase kinetics and power Myosin molecular motors generate forces in the cell and act as outputs in response to mechanical loads (3). Although many mechanosensors, adjusting their power outputs in response to studies have elucidated structural elements important for force mechanical loads. Little is known about the structural elements generation in myosin motors, not much is known about the re- involved in myosin mechanosensing. Our results identify the gions important for tuning a myosin’s ability to modulate power N-terminal region (NTR) of the myosin-I protein as having an output in response to mechanical loads. important role in tuning mechanochemistry. Appending the An opportunity to study these structural elements has emerged NTR from a highly tension-sensitive myosin (Myo1b) onto a less with the structural and mechanochemical characterization of two tension-sensitive motor (Myo1c) changes the identity of the myosin-I family members with similar sequences, Myosin-Ib primary force-sensitive transition of Myo1c, making it sensitive < (Myo1b) (4–7) and Myosin-Ic (Myo1c) (8–10). These motors have to forces 2 pN. Moreover, we show that the NTR stabilizes the – similar unloaded ATPase kinetics, where they are both low duty- post power-stroke conformation. These results identify the ratio motors (i.e., they spend a majority of their biochemical cycles NTR as an important structural element in myosin force sensing detached from actin) with motility rates that are limited by the rate and suggest a mechanism for generating diversity of function among myosin isoforms. of ADP release (7, 10–14). Although these motors have similar sequences and unloaded ATPase kinetics, they have very different Author contributions: M.J.G., H.S., and E.M.O. designed research; M.J.G. and T.L. per- mechanical outputs under load (for review, see ref. 15). Myo1b is formed research; M.J.G., T.L., and H.S. contributed new reagents/analytic tools; M.J.G., extraordinarily sensitive to small loads, where forces of 1 pN slow T.L., H.S., and E.M.O. analyzed data; and M.J.G., H.S., and E.M.O. wrote the paper. its motility rate more than 50-fold. As such, Myo1b has the The authors declare no conflict of interest. expected properties of a tension-sensitive anchor (5, 6). In contrast, This article is a PNAS Direct Submission. 1 pN of force does not appreciably slow the rate of Myo1c motility, 1To whom correspondence should be addressed. Email: [email protected]. enabling the motor to generate power over a range of forces. Thus, This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10. Myo1c has the expected properties of a slow transporter (10). Not 1073/pnas.1506633112/-/DCSupplemental. www.pnas.org/cgi/doi/10.1073/pnas.1506633112 PNAS | Published online June 8, 2015 | E3337–E3344 Downloaded by guest on September 25, 2021 Scheme 1), where the rate of ADP release limits the Myo1c A motility rate at saturating [ATP] (10). We used stopped-flow transient kinetic techniques to determine whether these steps were altered by deletion or swapping of the NTR (Table 1; see Materials and Methods for details). The rate constant for ATP- induced dissociation was measured by mixing pyrene-labeled actomyosin with varying ATP concentrations (Fig. 2). Similar to Δ Myo1c (10), fluorescence transients obtained with Myo1c N Δ > and Myo1c N- b are best fitted by the sum of two exponential functions. The fast component has a hyperbolic dependence on the [ATP] (Fig. 2A) and was modeled as shown in Scheme 1 (20). Δ Δ > Both Myo1c N and Myo1c N- b have substantially accelerated L11 −1 maximal rates of ATP binding (k+2′ = 160 ± 4.6 s and 160 ± L10 − Δ Δ > 2.8 s 1 for Myo1c N and Myo1c N- b, respectively) compared with −1 Myo1c (k+2′ = 18 ± 0.99 s ; P < 0.001). The rate of the slow M14 ΔN −1 phase measured for both Myo1c (kslow = 56 ± 3.2 s )and ΔN->b −1 Myo1c (kslow = 54 ± 2.0 s )is>10-foldfasterthanthat −1 found for Myo1c (kslow = 4.0 ± 0.034 s ; P < 0.001) (Fig. 2B). In Myo1c, the slow phase is due to an isomerization of actin-bound myosin from a nucleotide-free state that is not capable of binding ATP to a state than can bind ATP (12, 21); however, it does not B 10 20 30 appear that the slow phase observed for the NTR mutants cor- Myo1b MAKKEVKSSLLDNMIGVGDTVLLEPLN-EETF ID relates with the same transition (see below). Myo1c ---MESALTARD-RVGVQDFVLLENFTSEAAFIE The rate of ADP release was measured by preincubating NTR 10 20 30 pyrene-labeled actomyosin with saturating [ADP] and then ob- C serving the increase in fluorescence upon ATP-induced acto- 110 767 myosin dissociation (Fig. 2D). The rate of ADP release from k ′ = ± −1 MESALTARDRVGV Myo1c Motor IQ IQ IQ AviTag Myo1c ( +5 3.9 0.060 s ) was reported previously (10). For Myo1c ΔN ΔN Myo1c , the fluorescence transient is best described by the Myo1c MVGV Myo1c Motor IQ IQ IQ AviTag sum of two exponential functions where the slower phase (0.93 ± −1 ΔN->b Myo1c Motor IQ IQ IQ AviTag 0.010 s ) makes up 79% of the amplitude and the faster phase Myo1c MAKKEVKSSLLDNMVGV − Δ > (4.2 ± 0.18 s 1) makes up 21% of the amplitude.
Load more

Recommended publications
  • Prox1regulates the Subtype-Specific Development of Caudal Ganglionic
    The Journal of Neuroscience, September 16, 2015 • 35(37):12869–12889 • 12869 Development/Plasticity/Repair Prox1 Regulates the Subtype-Specific Development of Caudal Ganglionic Eminence-Derived GABAergic Cortical Interneurons X Goichi Miyoshi,1 Allison Young,1 Timothy Petros,1 Theofanis Karayannis,1 Melissa McKenzie Chang,1 Alfonso Lavado,2 Tomohiko Iwano,3 Miho Nakajima,4 Hiroki Taniguchi,5 Z. Josh Huang,5 XNathaniel Heintz,4 Guillermo Oliver,2 Fumio Matsuzaki,3 Robert P. Machold,1 and Gord Fishell1 1Department of Neuroscience and Physiology, NYU Neuroscience Institute, Smilow Research Center, New York University School of Medicine, New York, New York 10016, 2Department of Genetics & Tumor Cell Biology, St. Jude Children’s Research Hospital, Memphis, Tennessee 38105, 3Laboratory for Cell Asymmetry, RIKEN Center for Developmental Biology, Kobe 650-0047, Japan, 4Laboratory of Molecular Biology, Howard Hughes Medical Institute, GENSAT Project, The Rockefeller University, New York, New York 10065, and 5Cold Spring Harbor Laboratory, Cold Spring Harbor, New York 11724 Neurogliaform (RELNϩ) and bipolar (VIPϩ) GABAergic interneurons of the mammalian cerebral cortex provide critical inhibition locally within the superficial layers. While these subtypes are known to originate from the embryonic caudal ganglionic eminence (CGE), the specific genetic programs that direct their positioning, maturation, and integration into the cortical network have not been eluci- dated. Here, we report that in mice expression of the transcription factor Prox1 is selectively maintained in postmitotic CGE-derived cortical interneuron precursors and that loss of Prox1 impairs the integration of these cells into superficial layers. Moreover, Prox1 differentially regulates the postnatal maturation of each specific subtype originating from the CGE (RELN, Calb2/VIP, and VIP).
    [Show full text]
  • High-Resolution Cryo-EM Structures of Actin-Bound Myosin States Reveal the Mechanism of Myosin Force Sensing
    High-resolution cryo-EM structures of actin-bound myosin states reveal the mechanism of myosin force sensing Ahmet Mentesa,b,c,1, Andrew Huehnd,1, Xueqi Liud, Adam Zwolaka,b, Roberto Domingueza,b, Henry Shumana,b,2, E. Michael Ostapa,b,c,2, and Charles V. Sindelard,2 aPennsylvania Muscle Institute, Perelman School of Medicine at the University of Pennsylvania, Philadelphia, PA 19104; bDepartment of Physiology, Perelman School of Medicine at the University of Pennsylvania, Philadelphia, PA 19104; cCenter for Engineering Mechanobiology, Perelman School of Medicine at the University of Pennsylvania, Philadelphia, PA 19104; and dDepartment Molecular Biophysics and Biochemistry, Yale University, New Haven, CT 06520 Edited by James R. Sellers, Laboratory of Molecular Physiology, National Heart, Lung, and Blood Institute, National Institutes of Health, Bethesda, MD, and accepted by Editorial Board Member Edward D. Korn December 15, 2017 (received for review October 19, 2017) Myosins adjust their power outputs in response to mechanical in the inhibition of MgADP release upon a restraining force on loads in an isoform-dependent manner, resulting in their ability to the lever. Additionally, we provide the high-resolution structure of dynamically adapt to a range of motile challenges. Here, we reveal the actin binding interface of myo1b, finding that, despite the the structural basis for force-sensing based on near-atomic conserved spatial topology of actin-binding loops, the precise resolution structures of one rigor and two ADP-bound states of nature of actin binding among myosins is quite diverse. Finally, we myosin-IB (myo1b) bound to actin, determined by cryo-electron provide a high-resolution structure of phalloidin bound to actin.
    [Show full text]
  • Exosomes in the Thymus: Antigen Transfer and Vesicles
    MINI REVIEW published: 20 July 2015 doi: 10.3389/fimmu.2015.00366 Exosomes in the thymus: antigen transfer and vesicles Gabriel Skogberg 1*, Esbjörn Telemo 1 and Olov Ekwall 1,2 1 Department of Rheumatology and Inflammation Research, Institute of Medicine, The Sahlgrenska Academy, Gothenburg University, Gothenburg, Sweden, 2 Department of Pediatrics, Institute of Clinical Sciences, The Sahlgrenska Academy, Gothenburg University, Gothenburg, Sweden Thymocytes go through several steps of maturation and selection in the thymus in order to form a functional pool of effector T-cells and regulatory T-cells in the periphery. Close interactions between thymocytes, thymic epithelial cells, and dendritic cells are of vital importance for the maturation, selection, and lineage decision of the thymocytes. One important question that is still unanswered is how a relatively small epithelial cell population can present a vast array of self-antigens to the manifold larger population of developing thymocytes in this selection process. Here, we review and discuss the literature concerning antigen transfer from epithelial cells with a focus on exosomes. Exosomes are nano-sized vesicles released from a cell into the extracellular space. These vesicles can carry proteins, microRNAs, and mRNAs between cells and are thus able to Edited by: Geraldo Aleixo Passos, participate in intercellular communication. Exosomes have been shown to be produced by University of São Paulo, Brazil thymic epithelial cells and to carry tissue-restricted antigens and MHC molecules, which Reviewed by: may enable them to participate in the thymocyte selection process. Bin Li, Chinese Academy of Sciences, China Keywords: exosome, thymic epithelial cell, tolerance, tissue-restricted antigen, miRNA Nuno L.
    [Show full text]
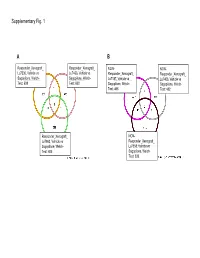
  • Supplementary Data
    Supplementary Fig. 1 A B Responder_Xenograft_ Responder_Xenograft_ NON- NON- Lu7336, Vehicle vs Lu7466, Vehicle vs Responder_Xenograft_ Responder_Xenograft_ Sagopilone, Welch- Sagopilone, Welch- Lu7187, Vehicle vs Lu7406, Vehicle vs Test: 638 Test: 600 Sagopilone, Welch- Sagopilone, Welch- Test: 468 Test: 482 Responder_Xenograft_ NON- Lu7860, Vehicle vs Responder_Xenograft_ Sagopilone, Welch - Lu7558, Vehicle vs Test: 605 Sagopilone, Welch- Test: 333 Supplementary Fig. 2 Supplementary Fig. 3 Supplementary Figure S1. Venn diagrams comparing probe sets regulated by Sagopilone treatment (10mg/kg for 24h) between individual models (Welsh Test ellipse p-value<0.001 or 5-fold change). A Sagopilone responder models, B Sagopilone non-responder models. Supplementary Figure S2. Pathway analysis of genes regulated by Sagopilone treatment in responder xenograft models 24h after Sagopilone treatment by GeneGo Metacore; the most significant pathway map representing cell cycle/spindle assembly and chromosome separation is shown, genes upregulated by Sagopilone treatment are marked with red thermometers. Supplementary Figure S3. GeneGo Metacore pathway analysis of genes differentially expressed between Sagopilone Responder and Non-Responder models displaying –log(p-Values) of most significant pathway maps. Supplementary Tables Supplementary Table 1. Response and activity in 22 non-small-cell lung cancer (NSCLC) xenograft models after treatment with Sagopilone and other cytotoxic agents commonly used in the management of NSCLC Tumor Model Response type
    [Show full text]
  • Quantitative SUMO Proteomics Reveals the Modulation of Several
    www.nature.com/scientificreports OPEN Quantitative SUMO proteomics reveals the modulation of several PML nuclear body associated Received: 10 October 2017 Accepted: 28 March 2018 proteins and an anti-senescence Published: xx xx xxxx function of UBC9 Francis P. McManus1, Véronique Bourdeau2, Mariana Acevedo2, Stéphane Lopes-Paciencia2, Lian Mignacca2, Frédéric Lamoliatte1,3, John W. Rojas Pino2, Gerardo Ferbeyre2 & Pierre Thibault1,3 Several regulators of SUMOylation have been previously linked to senescence but most targets of this modifcation in senescent cells remain unidentifed. Using a two-step purifcation of a modifed SUMO3, we profled the SUMO proteome of senescent cells in a site-specifc manner. We identifed 25 SUMO sites on 23 proteins that were signifcantly regulated during senescence. Of note, most of these proteins were PML nuclear body (PML-NB) associated, which correlates with the increased number and size of PML-NBs observed in senescent cells. Interestingly, the sole SUMO E2 enzyme, UBC9, was more SUMOylated during senescence on its Lys-49. Functional studies of a UBC9 mutant at Lys-49 showed a decreased association to PML-NBs and the loss of UBC9’s ability to delay senescence. We thus propose both pro- and anti-senescence functions of protein SUMOylation. Many cellular mechanisms of defense have evolved to reduce the onset of tumors and potential cancer develop- ment. One such mechanism is cellular senescence where cells undergo cell cycle arrest in response to various stressors1,2. Multiple triggers for the onset of senescence have been documented. While replicative senescence is primarily caused in response to telomere shortening3,4, senescence can also be triggered early by a number of exogenous factors including DNA damage, elevated levels of reactive oxygen species (ROS), high cytokine signa- ling, and constitutively-active oncogenes (such as H-RAS-G12V)5,6.
    [Show full text]
  • Identification of the Fatty Acid Synthase Interaction Network Via Itraq-Based Proteomics Indicates the Potential Molecular Mecha
    Huang et al. Cancer Cell Int (2020) 20:332 https://doi.org/10.1186/s12935-020-01409-2 Cancer Cell International PRIMARY RESEARCH Open Access Identifcation of the fatty acid synthase interaction network via iTRAQ-based proteomics indicates the potential molecular mechanisms of liver cancer metastasis Juan Huang1, Yao Tang1, Xiaoqin Zou1, Yi Lu1, Sha She1, Wenyue Zhang1, Hong Ren1, Yixuan Yang1,2* and Huaidong Hu1,2* Abstract Background: Fatty acid synthase (FASN) is highly expressed in various types of cancer and has an important role in carcinogenesis and metastasis. To clarify the mechanisms of FASN in liver cancer invasion and metastasis, the FASN protein interaction network in liver cancer was identifed by targeted proteomic analysis. Methods: Wound healing and Transwell assays was performed to observe the efect of FASN during migration and invasion in liver cancer. Isobaric tags for relative and absolute quantitation (iTRAQ)-based mass spectrometry were used to identify proteins interacting with FASN in HepG2 cells. Diferential expressed proteins were validated by co-immunoprecipitation, western blot analyses and confocal microscopy. Western blot and reverse transcription- quantitative polymerase chain reaction (RT-qPCR) were performed to demonstrate the mechanism of FASN regulating metastasis. Results: FASN knockdown inhibited migration and invasion of HepG2 and SMMC7721 cells. A total of, 79 proteins interacting with FASN were identifed. Additionally, gene ontology term enrichment analysis indicated that the majority of biological regulation and cellular processes that the FASN-interacting proteins were associated with. Co- precipitation and co-localization of FASN with fascin actin-bundling protein 1 (FSCN1), signal-induced proliferation- associated 1 (SIPA1), spectrin β, non-erythrocytic 1 (SPTBN1) and CD59 were evaluated.
    [Show full text]
  • Inhibition of the MID1 Protein Complex
    Matthes et al. Cell Death Discovery (2018) 4:4 DOI 10.1038/s41420-017-0003-8 Cell Death Discovery ARTICLE Open Access Inhibition of the MID1 protein complex: a novel approach targeting APP protein synthesis Frank Matthes1,MoritzM.Hettich1, Judith Schilling1, Diana Flores-Dominguez1, Nelli Blank1, Thomas Wiglenda2, Alexander Buntru2,HannaWolf1, Stephanie Weber1,InaVorberg 1, Alina Dagane2, Gunnar Dittmar2,3,ErichWanker2, Dan Ehninger1 and Sybille Krauss1 Abstract Alzheimer’s disease (AD) is characterized by two neuropathological hallmarks: senile plaques, which are composed of amyloid-β (Aβ) peptides, and neurofibrillary tangles, which are composed of hyperphosphorylated tau protein. Aβ peptides are derived from sequential proteolytic cleavage of the amyloid precursor protein (APP). In this study, we identified a so far unknown mode of regulation of APP protein synthesis involving the MID1 protein complex: MID1 binds to and regulates the translation of APP mRNA. The underlying mode of action of MID1 involves the mTOR pathway. Thus, inhibition of the MID1 complex reduces the APP protein level in cultures of primary neurons. Based on this, we used one compound that we discovered previously to interfere with the MID1 complex, metformin, for in vivo experiments. Indeed, long-term treatment with metformin decreased APP protein expression levels and consequently Aβ in an AD mouse model. Importantly, we have initiated the metformin treatment late in life, at a time-point where mice were in an already progressed state of the disease, and could observe an improved behavioral phenotype. These 1234567890 1234567890 findings together with our previous observation, showing that inhibition of the MID1 complex by metformin also decreases tau phosphorylation, make the MID1 complex a particularly interesting drug target for treating AD.
    [Show full text]
  • Product Size GOT1 P00504 F CAAGCTGT
    Table S1. List of primer sequences for RT-qPCR. Gene Product Uniprot ID F/R Sequence(5’-3’) name size GOT1 P00504 F CAAGCTGTCAAGCTGCTGTC 71 R CGTGGAGGAAAGCTAGCAAC OGDHL E1BTL0 F CCCTTCTCACTTGGAAGCAG 81 R CCTGCAGTATCCCCTCGATA UGT2A1 F1NMB3 F GGAGCAAAGCACTTGAGACC 93 R GGCTGCACAGATGAACAAGA GART P21872 F GGAGATGGCTCGGACATTTA 90 R TTCTGCACATCCTTGAGCAC GSTT1L E1BUB6 F GTGCTACCGAGGAGCTGAAC 105 R CTACGAGGTCTGCCAAGGAG IARS Q5ZKA2 F GACAGGTTTCCTGGCATTGT 148 R GGGCTTGATGAACAACACCT RARS Q5ZM11 F TCATTGCTCACCTGCAAGAC 146 R CAGCACCACACATTGGTAGG GSS F1NLE4 F ACTGGATGTGGGTGAAGAGG 89 R CTCCTTCTCGCTGTGGTTTC CYP2D6 F1NJG4 F AGGAGAAAGGAGGCAGAAGC 113 R TGTTGCTCCAAGATGACAGC GAPDH P00356 F GACGTGCAGCAGGAACACTA 112 R CTTGGACTTTGCCAGAGAGG Table S2. List of differentially expressed proteins during chronic heat stress. score name Description MW PI CC CH Down regulated by chronic heat stress A2M Uncharacterized protein 158 1 0.35 6.62 A2ML4 Uncharacterized protein 163 1 0.09 6.37 ABCA8 Uncharacterized protein 185 1 0.43 7.08 ABCB1 Uncharacterized protein 152 1 0.47 8.43 ACOX2 Cluster of Acyl-coenzyme A oxidase 75 1 0.21 8 ACTN1 Alpha-actinin-1 102 1 0.37 5.55 ALDOC Cluster of Fructose-bisphosphate aldolase 39 1 0.5 6.64 AMDHD1 Cluster of Uncharacterized protein 37 1 0.04 6.76 AMT Aminomethyltransferase, mitochondrial 42 1 0.29 9.14 AP1B1 AP complex subunit beta 103 1 0.15 5.16 APOA1BP NAD(P)H-hydrate epimerase 32 1 0.4 8.62 ARPC1A Actin-related protein 2/3 complex subunit 42 1 0.34 8.31 ASS1 Argininosuccinate synthase 47 1 0.04 6.67 ATP2A2 Cluster of Calcium-transporting
    [Show full text]
  • Myosin 1B Flattens and Prunes Branched Actin Filaments
    bioRxiv preprint doi: https://doi.org/10.1101/2020.02.26.966663; this version posted February 27, 2020. The copyright holder for this preprint (which was not certified by peer review) is the author/funder. All rights reserved. No reuse allowed without permission. Myosin 1b Flattens and Prunes Branched Actin Filaments. Julien Pernier1,2,3, Antoine Morchain1,2, Valentina Caorsi4, Aurélie Bertin1,2, Hugo Bousquet2,3, Patricia Bassereau1,2*, Evelyne Coudrier2,3* 1. Laboratoire Physico-Chimie Curie, Institut Curie, PSL Research University, CNRS UMR168, 75005 Paris, France 2. Sorbonne Université, 75005 Paris, France 3. Institut Curie, PSL Research University, C.N.R.S. UMR 144, 26 rue d’Ulm, Paris, France 4. Abbelight, 191 avenue Aristide Briand, 94230 Cachan, France *: corresponding authors: [email protected] and [email protected] 1 bioRxiv preprint doi: https://doi.org/10.1101/2020.02.26.966663; this version posted February 27, 2020. The copyright holder for this preprint (which was not certified by peer review) is the author/funder. All rights reserved. No reuse allowed without permission. Abstract Motile and morphological cellular processes require a spatially and temporally coordinated branched actin network that is controlled by the activity of various regulatory proteins including the Arp2/3 complex, profilin, cofilin and tropomyosin. We have previously reported that myosin 1b regulates the density of the actin network in the growth cone. Using in vitro F-actin gliding assays and total internal reflection fluorescence (TIRF) microscopy we show in this report that this molecular motor flattens the Arp2/3-dependent actin branches up to breaking them and reduces the probability to form new branches.
    [Show full text]
  • Program in Human Neutrophils Fails To
    Downloaded from http://www.jimmunol.org/ by guest on September 25, 2021 is online at: average * The Journal of Immunology Anaplasma phagocytophilum , 20 of which you can access for free at: 2005; 174:6364-6372; ; from submission to initial decision 4 weeks from acceptance to publication J Immunol doi: 10.4049/jimmunol.174.10.6364 http://www.jimmunol.org/content/174/10/6364 Insights into Pathogen Immune Evasion Mechanisms: Fails to Induce an Apoptosis Differentiation Program in Human Neutrophils Dori L. Borjesson, Scott D. Kobayashi, Adeline R. Whitney, Jovanka M. Voyich, Cynthia M. Argue and Frank R. DeLeo cites 28 articles Submit online. Every submission reviewed by practicing scientists ? is published twice each month by Receive free email-alerts when new articles cite this article. Sign up at: http://jimmunol.org/alerts http://jimmunol.org/subscription Submit copyright permission requests at: http://www.aai.org/About/Publications/JI/copyright.html http://www.jimmunol.org/content/suppl/2005/05/03/174.10.6364.DC1 This article http://www.jimmunol.org/content/174/10/6364.full#ref-list-1 Information about subscribing to The JI No Triage! Fast Publication! Rapid Reviews! 30 days* • Why • • Material References Permissions Email Alerts Subscription Supplementary The Journal of Immunology The American Association of Immunologists, Inc., 1451 Rockville Pike, Suite 650, Rockville, MD 20852 Copyright © 2005 by The American Association of Immunologists All rights reserved. Print ISSN: 0022-1767 Online ISSN: 1550-6606. This information is current as of September 25, 2021. The Journal of Immunology Insights into Pathogen Immune Evasion Mechanisms: Anaplasma phagocytophilum Fails to Induce an Apoptosis Differentiation Program in Human Neutrophils1 Dori L.
    [Show full text]
  • Master Regulator of Actin Filament Function in the Cytoskeleton Peter W
    © 2015. Published by The Company of Biologists Ltd | Journal of Cell Science (2015) 128, 2965-2974 doi:10.1242/jcs.172502 COMMENTARY Tropomyosin – master regulator of actin filament function in the cytoskeleton Peter W. Gunning1,*, Edna C. Hardeman1,*,‡, Pekka Lappalainen2,* and Daniel P. Mulvihill3,* ABSTRACT The discovery of Tpm in mammalian non-muscle cells in the mid- Tropomyosin (Tpm) isoforms are the master regulators of the 1970s by Elias Lazarides, naturally, led to the expectation that Tpm functions of individual actin filaments in fungi and metazoans. Tpms has a similar function in these cells compared with its role in skeletal are coiled-coil parallel dimers that form a head-to-tail polymer along muscle cells (Lazarides, 1975). Immunofluorescence experiments led the length of actin filaments. Yeast only has two Tpm isoforms, Lazarides to propose the existence of two populations of actin whereas mammals have over 40. Each cytoskeletal actin filament polymers in non-muscle cells, those that contained Tpm and those that contains a homopolymer of Tpm homodimers, resulting in a filament did not (Lazarides, 1976). In hindsight, it is difficult to understand of uniform Tpm composition along its length. Evidence for this ‘master how the discussion of the potential significance of Tpm as a core regulator’ role is based on four core sets of observation. First, spatially component of the actin filament in the non-muscle cytoskeleton and functionally distinct actin filaments contain different Tpm slowly disappeared from the literature. There are several simple isoforms, and recent data suggest that members of the formin explanations that are likely to account for this.
    [Show full text]
  • Comparative Itraq Proteomics Revealed Proteins Associated With
    Li et al. Proteome Science (2018) 16:14 https://doi.org/10.1186/s12953-018-0141-9 RESEARCH Open Access Comparative iTRAQ proteomics revealed proteins associated with horn development in yak Mingna Li, Xiaoyun Wu, Xian Guo, Pengjia Bao, Xuezhi Ding, Min Chu, Chunnian Liang and Ping Yan* Abstract Background: The practice of dehorning yak raises animal safety concerns, which have been addressed by selective breeding to obtain genetically hornless yak. The POLLED locus in yak has been studied extensively; however, little is known regarding the proteins that regulate horn bud development. Methods: A differential proteomic analysis was performed to compare the skin from the horn bud region of polled yak fetuses and the horn bud tissue of horned yak fetuses using isobaric tags for relative and absolute quantitation (iTRAQ) technology coupled with 2D LC-MS/MS. Results: One hundred differentially abundant proteins (DAPs) were identified. Of these, 29 were up-regulated and 71 were down-regulated in skin from the horn bud region of polled fetuses when compared to the horn bud tissue of horned fetuses. Bioinformatics analyses showed that the up-regulated DAPs were mainly associated with metabolic activities, while the down-regulated DAPs were significantly enriched in cell adhesion and cell movement activities. Conclusions: We concluded that some important proteins were associated with cell adhesion, cell motility, keratinocyte differentiation, cytoskeleton organization, osteoblast differentiation, and fatty acid metabolism during horn bud development. These results advance our understanding of the molecular mechanisms underlying horn development. Keywords: Horn bud, iTRAQ, Proteomics, Yak (Bos grunniens) Background Yak and cattle are related species belonging to the The yak is an important domesticated species found in same genus.
    [Show full text]