Myosin IC Generates Power Over a Range of Loads Via a New Tension
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Human Periprostatic Adipose Tissue: Secretome from Patients With
CANCER GENOMICS & PROTEOMICS 16 : 29-58 (2019) doi:10.21873/cgp.20110 Human Periprostatic Adipose Tissue: Secretome from Patients With Prostate Cancer or Benign Prostate Hyperplasia PAULA ALEJANDRA SACCA 1, OSVALDO NÉSTOR MAZZA 2, CARLOS SCORTICATI 2, GONZALO VITAGLIANO 3, GABRIEL CASAS 4 and JUAN CARLOS CALVO 1,5 1Institute of Biology and Experimental Medicine (IBYME), CONICET, Buenos Aires, Argentina; 2Department of Urology, School of Medicine, University of Buenos Aires, Clínical Hospital “José de San Martín”, Buenos Aires, Argentina; 3Department of Urology, Deutsches Hospital, Buenos Aires, Argentina; 4Department of Pathology, Deutsches Hospital, Buenos Aires, Argentina; 5Department of Biological Chemistry, School of Exact and Natural Sciences, University of Buenos Aires, Buenos Aires, Argentina Abstract. Background/Aim: Periprostatic adipose tissue Prostate cancer (PCa) is the second most common cancer in (PPAT) directs tumour behaviour. Microenvironment secretome men worldwide. While most men have indolent disease, provides information related to its biology. This study was which can be treated properly, the problem consists in performed to identify secreted proteins by PPAT, from both reliably distinguishing between indolent and aggressive prostate cancer and benign prostate hyperplasia (BPH) disease. Evidence shows that the microenvironment affects patients. Patients and Methods: Liquid chromatography-mass tumour behavior. spectrometry-based proteomic analysis was performed in Adipose tissue microenvironment is now known to direct PPAT-conditioned media (CM) from patients with prostate tumour growth, invasion and metastases (1, 2). Adipose cancer (CMs-T) (stage T3: CM-T3, stage T2: CM-T2) or tissue is adjacent to the prostate gland and the site of benign disease (CM-BPH). Results: The highest number and invasion of PCa. -

A Computational Approach for Defining a Signature of Β-Cell Golgi Stress in Diabetes Mellitus
Page 1 of 781 Diabetes A Computational Approach for Defining a Signature of β-Cell Golgi Stress in Diabetes Mellitus Robert N. Bone1,6,7, Olufunmilola Oyebamiji2, Sayali Talware2, Sharmila Selvaraj2, Preethi Krishnan3,6, Farooq Syed1,6,7, Huanmei Wu2, Carmella Evans-Molina 1,3,4,5,6,7,8* Departments of 1Pediatrics, 3Medicine, 4Anatomy, Cell Biology & Physiology, 5Biochemistry & Molecular Biology, the 6Center for Diabetes & Metabolic Diseases, and the 7Herman B. Wells Center for Pediatric Research, Indiana University School of Medicine, Indianapolis, IN 46202; 2Department of BioHealth Informatics, Indiana University-Purdue University Indianapolis, Indianapolis, IN, 46202; 8Roudebush VA Medical Center, Indianapolis, IN 46202. *Corresponding Author(s): Carmella Evans-Molina, MD, PhD ([email protected]) Indiana University School of Medicine, 635 Barnhill Drive, MS 2031A, Indianapolis, IN 46202, Telephone: (317) 274-4145, Fax (317) 274-4107 Running Title: Golgi Stress Response in Diabetes Word Count: 4358 Number of Figures: 6 Keywords: Golgi apparatus stress, Islets, β cell, Type 1 diabetes, Type 2 diabetes 1 Diabetes Publish Ahead of Print, published online August 20, 2020 Diabetes Page 2 of 781 ABSTRACT The Golgi apparatus (GA) is an important site of insulin processing and granule maturation, but whether GA organelle dysfunction and GA stress are present in the diabetic β-cell has not been tested. We utilized an informatics-based approach to develop a transcriptional signature of β-cell GA stress using existing RNA sequencing and microarray datasets generated using human islets from donors with diabetes and islets where type 1(T1D) and type 2 diabetes (T2D) had been modeled ex vivo. To narrow our results to GA-specific genes, we applied a filter set of 1,030 genes accepted as GA associated. -

Protein Identities in Evs Isolated from U87-MG GBM Cells As Determined by NG LC-MS/MS
Protein identities in EVs isolated from U87-MG GBM cells as determined by NG LC-MS/MS. No. Accession Description Σ Coverage Σ# Proteins Σ# Unique Peptides Σ# Peptides Σ# PSMs # AAs MW [kDa] calc. pI 1 A8MS94 Putative golgin subfamily A member 2-like protein 5 OS=Homo sapiens PE=5 SV=2 - [GG2L5_HUMAN] 100 1 1 7 88 110 12,03704523 5,681152344 2 P60660 Myosin light polypeptide 6 OS=Homo sapiens GN=MYL6 PE=1 SV=2 - [MYL6_HUMAN] 100 3 5 17 173 151 16,91913397 4,652832031 3 Q6ZYL4 General transcription factor IIH subunit 5 OS=Homo sapiens GN=GTF2H5 PE=1 SV=1 - [TF2H5_HUMAN] 98,59 1 1 4 13 71 8,048185945 4,652832031 4 P60709 Actin, cytoplasmic 1 OS=Homo sapiens GN=ACTB PE=1 SV=1 - [ACTB_HUMAN] 97,6 5 5 35 917 375 41,70973209 5,478027344 5 P13489 Ribonuclease inhibitor OS=Homo sapiens GN=RNH1 PE=1 SV=2 - [RINI_HUMAN] 96,75 1 12 37 173 461 49,94108966 4,817871094 6 P09382 Galectin-1 OS=Homo sapiens GN=LGALS1 PE=1 SV=2 - [LEG1_HUMAN] 96,3 1 7 14 283 135 14,70620005 5,503417969 7 P60174 Triosephosphate isomerase OS=Homo sapiens GN=TPI1 PE=1 SV=3 - [TPIS_HUMAN] 95,1 3 16 25 375 286 30,77169764 5,922363281 8 P04406 Glyceraldehyde-3-phosphate dehydrogenase OS=Homo sapiens GN=GAPDH PE=1 SV=3 - [G3P_HUMAN] 94,63 2 13 31 509 335 36,03039959 8,455566406 9 Q15185 Prostaglandin E synthase 3 OS=Homo sapiens GN=PTGES3 PE=1 SV=1 - [TEBP_HUMAN] 93,13 1 5 12 74 160 18,68541938 4,538574219 10 P09417 Dihydropteridine reductase OS=Homo sapiens GN=QDPR PE=1 SV=2 - [DHPR_HUMAN] 93,03 1 1 17 69 244 25,77302971 7,371582031 11 P01911 HLA class II histocompatibility antigen, -

Prox1regulates the Subtype-Specific Development of Caudal Ganglionic
The Journal of Neuroscience, September 16, 2015 • 35(37):12869–12889 • 12869 Development/Plasticity/Repair Prox1 Regulates the Subtype-Specific Development of Caudal Ganglionic Eminence-Derived GABAergic Cortical Interneurons X Goichi Miyoshi,1 Allison Young,1 Timothy Petros,1 Theofanis Karayannis,1 Melissa McKenzie Chang,1 Alfonso Lavado,2 Tomohiko Iwano,3 Miho Nakajima,4 Hiroki Taniguchi,5 Z. Josh Huang,5 XNathaniel Heintz,4 Guillermo Oliver,2 Fumio Matsuzaki,3 Robert P. Machold,1 and Gord Fishell1 1Department of Neuroscience and Physiology, NYU Neuroscience Institute, Smilow Research Center, New York University School of Medicine, New York, New York 10016, 2Department of Genetics & Tumor Cell Biology, St. Jude Children’s Research Hospital, Memphis, Tennessee 38105, 3Laboratory for Cell Asymmetry, RIKEN Center for Developmental Biology, Kobe 650-0047, Japan, 4Laboratory of Molecular Biology, Howard Hughes Medical Institute, GENSAT Project, The Rockefeller University, New York, New York 10065, and 5Cold Spring Harbor Laboratory, Cold Spring Harbor, New York 11724 Neurogliaform (RELNϩ) and bipolar (VIPϩ) GABAergic interneurons of the mammalian cerebral cortex provide critical inhibition locally within the superficial layers. While these subtypes are known to originate from the embryonic caudal ganglionic eminence (CGE), the specific genetic programs that direct their positioning, maturation, and integration into the cortical network have not been eluci- dated. Here, we report that in mice expression of the transcription factor Prox1 is selectively maintained in postmitotic CGE-derived cortical interneuron precursors and that loss of Prox1 impairs the integration of these cells into superficial layers. Moreover, Prox1 differentially regulates the postnatal maturation of each specific subtype originating from the CGE (RELN, Calb2/VIP, and VIP). -

High-Resolution Cryo-EM Structures of Actin-Bound Myosin States Reveal the Mechanism of Myosin Force Sensing
High-resolution cryo-EM structures of actin-bound myosin states reveal the mechanism of myosin force sensing Ahmet Mentesa,b,c,1, Andrew Huehnd,1, Xueqi Liud, Adam Zwolaka,b, Roberto Domingueza,b, Henry Shumana,b,2, E. Michael Ostapa,b,c,2, and Charles V. Sindelard,2 aPennsylvania Muscle Institute, Perelman School of Medicine at the University of Pennsylvania, Philadelphia, PA 19104; bDepartment of Physiology, Perelman School of Medicine at the University of Pennsylvania, Philadelphia, PA 19104; cCenter for Engineering Mechanobiology, Perelman School of Medicine at the University of Pennsylvania, Philadelphia, PA 19104; and dDepartment Molecular Biophysics and Biochemistry, Yale University, New Haven, CT 06520 Edited by James R. Sellers, Laboratory of Molecular Physiology, National Heart, Lung, and Blood Institute, National Institutes of Health, Bethesda, MD, and accepted by Editorial Board Member Edward D. Korn December 15, 2017 (received for review October 19, 2017) Myosins adjust their power outputs in response to mechanical in the inhibition of MgADP release upon a restraining force on loads in an isoform-dependent manner, resulting in their ability to the lever. Additionally, we provide the high-resolution structure of dynamically adapt to a range of motile challenges. Here, we reveal the actin binding interface of myo1b, finding that, despite the the structural basis for force-sensing based on near-atomic conserved spatial topology of actin-binding loops, the precise resolution structures of one rigor and two ADP-bound states of nature of actin binding among myosins is quite diverse. Finally, we myosin-IB (myo1b) bound to actin, determined by cryo-electron provide a high-resolution structure of phalloidin bound to actin. -

Microrna Regulatory Pathways in the Control of the Actin–Myosin Cytoskeleton
cells Review MicroRNA Regulatory Pathways in the Control of the Actin–Myosin Cytoskeleton , , Karen Uray * y , Evelin Major and Beata Lontay * y Department of Medical Chemistry, Faculty of Medicine, University of Debrecen, 4032 Debrecen, Hungary; [email protected] * Correspondence: [email protected] (K.U.); [email protected] (B.L.); Tel.: +36-52-412345 (K.U. & B.L.) The authors contributed equally to the manuscript. y Received: 11 June 2020; Accepted: 7 July 2020; Published: 9 July 2020 Abstract: MicroRNAs (miRNAs) are key modulators of post-transcriptional gene regulation in a plethora of processes, including actin–myosin cytoskeleton dynamics. Recent evidence points to the widespread effects of miRNAs on actin–myosin cytoskeleton dynamics, either directly on the expression of actin and myosin genes or indirectly on the diverse signaling cascades modulating cytoskeletal arrangement. Furthermore, studies from various human models indicate that miRNAs contribute to the development of various human disorders. The potentially huge impact of miRNA-based mechanisms on cytoskeletal elements is just starting to be recognized. In this review, we summarize recent knowledge about the importance of microRNA modulation of the actin–myosin cytoskeleton affecting physiological processes, including cardiovascular function, hematopoiesis, podocyte physiology, and osteogenesis. Keywords: miRNA; actin; myosin; actin–myosin complex; Rho kinase; cancer; smooth muscle; hematopoiesis; stress fiber; gene expression; cardiovascular system; striated muscle; muscle cell differentiation; therapy 1. Introduction Actin–myosin interactions are the primary source of force generation in mammalian cells. Actin forms a cytoskeletal network and the myosin motor proteins pull actin filaments to produce contractile force. All eukaryotic cells contain an actin–myosin network inferring contractile properties to these cells. -

Novel Myosin Mutations for Hereditary Hearing Loss Revealed by Targeted Genomic Capture and Massively Parallel Sequencing
European Journal of Human Genetics (2014) 22, 768–775 & 2014 Macmillan Publishers Limited All rights reserved 1018-4813/14 www.nature.com/ejhg ARTICLE Novel myosin mutations for hereditary hearing loss revealed by targeted genomic capture and massively parallel sequencing Zippora Brownstein1,6, Amal Abu-Rayyan2,6, Daphne Karfunkel-Doron1, Serena Sirigu3, Bella Davidov4, Mordechai Shohat1,4, Moshe Frydman1,5, Anne Houdusse3, Moien Kanaan2 and Karen B Avraham*,1 Hereditary hearing loss is genetically heterogeneous, with a large number of genes and mutations contributing to this sensory, often monogenic, disease. This number, as well as large size, precludes comprehensive genetic diagnosis of all known deafness genes. A combination of targeted genomic capture and massively parallel sequencing (MPS), also referred to as next-generation sequencing, was applied to determine the deafness-causing genes in hearing-impaired individuals from Israeli Jewish and Palestinian Arab families. Among the mutations detected, we identified nine novel mutations in the genes encoding myosin VI, myosin VIIA and myosin XVA, doubling the number of myosin mutations in the Middle East. Myosin VI mutations were identified in this population for the first time. Modeling of the mutations provided predicted mechanisms for the damage they inflict in the molecular motors, leading to impaired function and thus deafness. The myosin mutations span all regions of these molecular motors, leading to a wide range of hearing phenotypes, reinforcing the key role of this family of proteins in auditory function. This study demonstrates that multiple mutations responsible for hearing loss can be identified in a relatively straightforward manner by targeted-gene MPS technology and concludes that this is the optimal genetic diagnostic approach for identification of mutations responsible for hearing loss. -

Exosomes in the Thymus: Antigen Transfer and Vesicles
MINI REVIEW published: 20 July 2015 doi: 10.3389/fimmu.2015.00366 Exosomes in the thymus: antigen transfer and vesicles Gabriel Skogberg 1*, Esbjörn Telemo 1 and Olov Ekwall 1,2 1 Department of Rheumatology and Inflammation Research, Institute of Medicine, The Sahlgrenska Academy, Gothenburg University, Gothenburg, Sweden, 2 Department of Pediatrics, Institute of Clinical Sciences, The Sahlgrenska Academy, Gothenburg University, Gothenburg, Sweden Thymocytes go through several steps of maturation and selection in the thymus in order to form a functional pool of effector T-cells and regulatory T-cells in the periphery. Close interactions between thymocytes, thymic epithelial cells, and dendritic cells are of vital importance for the maturation, selection, and lineage decision of the thymocytes. One important question that is still unanswered is how a relatively small epithelial cell population can present a vast array of self-antigens to the manifold larger population of developing thymocytes in this selection process. Here, we review and discuss the literature concerning antigen transfer from epithelial cells with a focus on exosomes. Exosomes are nano-sized vesicles released from a cell into the extracellular space. These vesicles can carry proteins, microRNAs, and mRNAs between cells and are thus able to Edited by: Geraldo Aleixo Passos, participate in intercellular communication. Exosomes have been shown to be produced by University of São Paulo, Brazil thymic epithelial cells and to carry tissue-restricted antigens and MHC molecules, which Reviewed by: may enable them to participate in the thymocyte selection process. Bin Li, Chinese Academy of Sciences, China Keywords: exosome, thymic epithelial cell, tolerance, tissue-restricted antigen, miRNA Nuno L. -

Genome-Wide Identification, Characterization and Expression
G C A T T A C G G C A T genes Article Genome-Wide Identification, Characterization and Expression Profiling of myosin Family Genes in Sebastes schlegelii Chaofan Jin 1, Mengya Wang 1,2, Weihao Song 1 , Xiangfu Kong 1, Fengyan Zhang 1, Quanqi Zhang 1,2,3 and Yan He 1,2,* 1 MOE Key Laboratory of Molecular Genetics and Breeding, College of Marine Life Sciences, Ocean University of China, Qingdao 266003, China; [email protected] (C.J.); [email protected] (M.W.); [email protected] (W.S.); [email protected] (X.K.); [email protected] (F.Z.); [email protected] (Q.Z.) 2 Laboratory of Tropical Marine Germplasm Resources and Breeding Engineering, Sanya Oceanographic Institution, Ocean University of China, Sanya 572000, China 3 Laboratory for Marine Fisheries Science and Food Production Processes, Qingdao National Laboratory for Marine Science and Technology, Qingdao 266003, China * Correspondence: [email protected]; Tel.: +86-0532-82031986 Abstract: Myosins are important eukaryotic motor proteins that bind actin and utilize the energy of ATP hydrolysis to perform a broad range of functions such as muscle contraction, cell migration, cytokinesis, and intracellular trafficking. However, the characterization and function of myosin is poorly studied in teleost fish. In this study, we identified 60 myosin family genes in a marine teleost, black rockfish (Sebastes schlegelii), and further characterized their expression patterns. myosin showed divergent expression patterns in adult tissues, indicating they are involved in different types and Citation: Jin, C.; Wang, M.; Song, W.; compositions of muscle fibers. Among 12 subfamilies, S. schlegelii myo2 subfamily was significantly Kong, X.; Zhang, F.; Zhang, Q.; He, Y. -
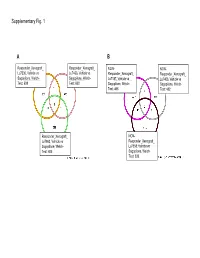
Supplementary Data
Supplementary Fig. 1 A B Responder_Xenograft_ Responder_Xenograft_ NON- NON- Lu7336, Vehicle vs Lu7466, Vehicle vs Responder_Xenograft_ Responder_Xenograft_ Sagopilone, Welch- Sagopilone, Welch- Lu7187, Vehicle vs Lu7406, Vehicle vs Test: 638 Test: 600 Sagopilone, Welch- Sagopilone, Welch- Test: 468 Test: 482 Responder_Xenograft_ NON- Lu7860, Vehicle vs Responder_Xenograft_ Sagopilone, Welch - Lu7558, Vehicle vs Test: 605 Sagopilone, Welch- Test: 333 Supplementary Fig. 2 Supplementary Fig. 3 Supplementary Figure S1. Venn diagrams comparing probe sets regulated by Sagopilone treatment (10mg/kg for 24h) between individual models (Welsh Test ellipse p-value<0.001 or 5-fold change). A Sagopilone responder models, B Sagopilone non-responder models. Supplementary Figure S2. Pathway analysis of genes regulated by Sagopilone treatment in responder xenograft models 24h after Sagopilone treatment by GeneGo Metacore; the most significant pathway map representing cell cycle/spindle assembly and chromosome separation is shown, genes upregulated by Sagopilone treatment are marked with red thermometers. Supplementary Figure S3. GeneGo Metacore pathway analysis of genes differentially expressed between Sagopilone Responder and Non-Responder models displaying –log(p-Values) of most significant pathway maps. Supplementary Tables Supplementary Table 1. Response and activity in 22 non-small-cell lung cancer (NSCLC) xenograft models after treatment with Sagopilone and other cytotoxic agents commonly used in the management of NSCLC Tumor Model Response type -

Quantitative SUMO Proteomics Reveals the Modulation of Several
www.nature.com/scientificreports OPEN Quantitative SUMO proteomics reveals the modulation of several PML nuclear body associated Received: 10 October 2017 Accepted: 28 March 2018 proteins and an anti-senescence Published: xx xx xxxx function of UBC9 Francis P. McManus1, Véronique Bourdeau2, Mariana Acevedo2, Stéphane Lopes-Paciencia2, Lian Mignacca2, Frédéric Lamoliatte1,3, John W. Rojas Pino2, Gerardo Ferbeyre2 & Pierre Thibault1,3 Several regulators of SUMOylation have been previously linked to senescence but most targets of this modifcation in senescent cells remain unidentifed. Using a two-step purifcation of a modifed SUMO3, we profled the SUMO proteome of senescent cells in a site-specifc manner. We identifed 25 SUMO sites on 23 proteins that were signifcantly regulated during senescence. Of note, most of these proteins were PML nuclear body (PML-NB) associated, which correlates with the increased number and size of PML-NBs observed in senescent cells. Interestingly, the sole SUMO E2 enzyme, UBC9, was more SUMOylated during senescence on its Lys-49. Functional studies of a UBC9 mutant at Lys-49 showed a decreased association to PML-NBs and the loss of UBC9’s ability to delay senescence. We thus propose both pro- and anti-senescence functions of protein SUMOylation. Many cellular mechanisms of defense have evolved to reduce the onset of tumors and potential cancer develop- ment. One such mechanism is cellular senescence where cells undergo cell cycle arrest in response to various stressors1,2. Multiple triggers for the onset of senescence have been documented. While replicative senescence is primarily caused in response to telomere shortening3,4, senescence can also be triggered early by a number of exogenous factors including DNA damage, elevated levels of reactive oxygen species (ROS), high cytokine signa- ling, and constitutively-active oncogenes (such as H-RAS-G12V)5,6. -

Identification of the Fatty Acid Synthase Interaction Network Via Itraq-Based Proteomics Indicates the Potential Molecular Mecha
Huang et al. Cancer Cell Int (2020) 20:332 https://doi.org/10.1186/s12935-020-01409-2 Cancer Cell International PRIMARY RESEARCH Open Access Identifcation of the fatty acid synthase interaction network via iTRAQ-based proteomics indicates the potential molecular mechanisms of liver cancer metastasis Juan Huang1, Yao Tang1, Xiaoqin Zou1, Yi Lu1, Sha She1, Wenyue Zhang1, Hong Ren1, Yixuan Yang1,2* and Huaidong Hu1,2* Abstract Background: Fatty acid synthase (FASN) is highly expressed in various types of cancer and has an important role in carcinogenesis and metastasis. To clarify the mechanisms of FASN in liver cancer invasion and metastasis, the FASN protein interaction network in liver cancer was identifed by targeted proteomic analysis. Methods: Wound healing and Transwell assays was performed to observe the efect of FASN during migration and invasion in liver cancer. Isobaric tags for relative and absolute quantitation (iTRAQ)-based mass spectrometry were used to identify proteins interacting with FASN in HepG2 cells. Diferential expressed proteins were validated by co-immunoprecipitation, western blot analyses and confocal microscopy. Western blot and reverse transcription- quantitative polymerase chain reaction (RT-qPCR) were performed to demonstrate the mechanism of FASN regulating metastasis. Results: FASN knockdown inhibited migration and invasion of HepG2 and SMMC7721 cells. A total of, 79 proteins interacting with FASN were identifed. Additionally, gene ontology term enrichment analysis indicated that the majority of biological regulation and cellular processes that the FASN-interacting proteins were associated with. Co- precipitation and co-localization of FASN with fascin actin-bundling protein 1 (FSCN1), signal-induced proliferation- associated 1 (SIPA1), spectrin β, non-erythrocytic 1 (SPTBN1) and CD59 were evaluated.