DOCSLIB.ORG

Book Review: the Golden Ratio, Volume 52, Number 3

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Book Review: the Golden Ratio, Volume 52, Number 3 Book Review The Golden Ratio Reviewed by George Markowsky The Golden Ratio were being made about Mario Livio the golden ratio. Broadway Books, 2003 The results of my re- Paperback, 304 pages, $14.95 search were published in ISBN 0-7679-0816-3 “Misconceptions about √ the Golden Ratio” (The The number (1 + 5)/2=1.618 … is widely College Mathematics known as the golden ratio, φ and phi. Phi appears Journal, Vol. 23, No. 1, in many different equations and formulas and has Jan. 1992, 2–19). This many interesting properties. Many people have paper debunks many of heard marvelous tales about phi and how it per- the more prominent meates art and nature. My first exposure to phi was claims about phi and in a comic book entitled Donald in Mathmagic documents their perva- Land, which later became an animated cartoon sive presence in the seen by millions of people. As I grew up I kept see- mathematical literature. ing the same “facts” repeated in many different For example, the name places, including popular books on mathematics, “golden ratio” is a nineteenth-century creation and is not an ancient name for phi. Furthermore, it various mathematics textbooks, newspapers, and does not appear that phi was used to design either even in scholarly papers. It seemed as if every- the Great Pyramid or the Parthenon. For example, body knew these basic “facts” about phi. the Parthenon is 228 feet and 1/8 inch long, 101 Around 1990 I decided to give a talk to the Uni- feet and 3.75 inches wide, and 45 feet and 1 inch versity of Maine Classics Club and thought that the high. Taking the obvious ratios of length/width golden ratio would be a fascinating topic for this and width/height yields the number 2.25, which is audience. During the preparation of the talk I col- quite far from phi, which is 1.618…. The number lected all of the usual stories about the golden 2.25 = 9/4 is the ratio of two squares, and further ratio being used to design the Great Pyramid and study indicated that the gate to the Acropolis was the Parthenon, as well as about its aesthetic prop- built using this same ratio. erties and its use by painters. I found the references It also does not appear that Leonardo da Vinci to be quite vague, and in the process of trying to used phi, nor is phi present in the proportions of make my talk more precise, I actually began to the United Nations building in New York. look up measurements of buildings. Much to my Furthermore, in a large number of informal audi- surprise, the results did not support the claims that ence participation events, I have found that peo- George Markowsky is professor of computer science at the ple do not pick golden rectangles more frequently University of Maine. His email address is markov@ than others (in fact, they are often picked less fre- maine.edu. quently than others), so that the statements about 344 NOTICES OF THE AMS VOLUME 52, NUMBER 3 the aesthetic superiority of phi do not stand up to analyzes them in the same manner. Later in the empirical tests. These claims and others are de- chapter he reproduces a diagram from my paper molished in my paper in some detail. (he attributes the diagram to me, but does not give Since publishing my paper, I have tried to get a reference) that shows forty-eight rectangles of dif- people, in particular mathematicians, to tell the ferent proportions that I have used a number of truth about phi. Phi has many interesting mathe- times to ask people which rectangle they find most matical properties that deserve to be brought to the pleasing. public’s attention. It is, however, a disservice to On p. 183 of his book, Livio states: mathematics to mix the interesting properties of phi with dubious claims about its importance in art, You can test yourself (or your friends) architecture, human anatomy, and aesthetics. on the question of which rectangle you Mario Livio’s book, The Golden Ratio, is a broad prefer best. Figure 84 shows a collection survey of the properties of phi. The book is some of forty-eight rectangles, all having the 270 pages long, counting ten appendices, and same height, but with their widths rang- bounces along describing various mathematical ing from 0.4 to 2.5 times their height. properties of phi, while at the same time trying to University of Maine mathematician astonish the reader. It is the constant desire to as- George Markowsky used this collection tonish the reader that gets Livio into trouble and in his own informal experiments. that is undoubtedly the source of the subtitle: The Interestingly, Livio does not reference my paper Story of Phi, the World’s Most Astonishing Number. and does not quote my conclusion: When I first heard about this book, I was hopeful that it would finally put many of the bogus stories In the experiments I have conducted so about phi to rest, but unfortunately this book does far, the most commonly selected rec- not quite do so. tangle is one with a ratio of 1.83. For example, in his discussion of the Parthenon, Also, Livio does not point out that there are ac- Livio quotes from my paper and gives proper at- tually two golden rectangles in the diagram—one tribution. However, I believe that he waffles on the is oriented with the long dimension horizontal and issue of whether phi was used in the design of the the other with the long dimension vertical. Parthenon. On p. 74 he states: Livio could have performed a valuable service to So, was the Golden Ratio used in the the mathematical community had he written an ac- Parthenon’s design? It is difficult to say curate book about phi that treated it in a balanced for sure. While most of the mathemat- manner and that consistently and thoroughly de- ical theorems concerning the Golden bunked the various misconceptions about phi that Ratio (or “extreme and mean ratio”) ap- continue to circulate. Throughout this book, Livio pear to have been formulated after the struggles with the problem of wanting to “amaze” Parthenon had been constructed, con- the public without going too far and losing re- siderable knowledge existed among the spectability, but unfortunately he does not suc- Pythagoreans prior to that. ceed in solving it. I take strong issue with his conclusion that it is He deserves credit for surveying a wide range difficult to say for sure whether phi was used in of sources about phi, but in my opinion he is very the construction of the Parthenon. It seems to me inconsistent in how he uses them. In some cases that to even entertain the notion there has to be he does an effective job of debunking nonsense, but some reason to believe that it was true. It is clear in others his debunking is halfhearted. In some that the Greeks were not as enamored of phi as peo- cases he omits data that would be harmful to es- ple became once it received the name golden ratio tablishing phi as the “most astonishing” number. in the nineteenth century. Calling phi division into Unfortunately, he also seems interested in spawn- mean and extreme ratio does not generate great ex- ing some new myths. citement on the part of artists and architects. I For example, on p. 9 he discusses Salvador Dali’s have found no credible evidence that phi was ever “Sacrament of the Last Supper”. The first “fact” that used by Greek artists and architects for any pro- we are presented with is that the canvas measures ject at all. approximately 105.5 inches by 65.75 inches, which In Chapter 7 of his book Livio discusses the “are in a Golden Ratio to each other.” The ratio possible presence of phi in various paintings and 105.5/65.75 is approximately 1.605, which is close its role in aesthetics. Again, he closely parallels my to, but not equal to phi. If it was important for the paper but does not cite the paper either in the text painting to have phi as the ratio of its width to or in the notes to the text. In his discussion of height, why not use a canvas of size approximately Leonardo da Vinci, Livio reproduces exactly the 106 inches by 66 inches, which has a ratio of 1.606, painting and drawing discussed in my paper and which is even closer to phi? We are next told that: MARCH 2005 NOTICES OF THE AMS 345 Perhaps more important, part of a huge the recurrence relation and not on the starting dodecahedron (…) is seen floating above points. In particular, pick any two positive integers the table and engulfing it. … As we shall and use the formula Fn = Fn−1 +2Fn−2. One will see in Chapter 4, regular solids (like the find that eventually the ratio of consecutive terms cube) that can be precisely enclosed by will approach 2. In this regard, phi is no more a sphere with all their corners resting amazing than just about any other number. on the sphere, and the dodecahedron in Livio devotes a fair amount of space to dis- particular, are intimately related to the cussing Luca Pacioli and his work on the “Divine Golden Ratio. Proportion”. Livio notes that Pacioli ends up rec- ommending a system of proportions for art not This paragraph is odd for a number of reasons.
Load more

Recommended publications
  • Space Reporter's Handbook Mission Supplement
    CBS News Space Reporter's Handbook - Mission Supplement Page 1 The CBS News Space Reporter's Handbook Mission Supplement Shuttle Mission STS-125: Hubble Space Telescope Servicing Mission 4 Written and Produced By William G. Harwood CBS News Space Analyst [email protected] CBS News 5/10/09 Page 2 CBS News Space Reporter's Handbook - Mission Supplement Revision History Editor's Note Mission-specific sections of the Space Reporter's Handbook are posted as flight data becomes available. Readers should check the CBS News "Space Place" web site in the weeks before a launch to download the latest edition: http://www.cbsnews.com/network/news/space/current.html DATE RELEASE NOTES 08/03/08 Initial STS-125 release 04/11/09 Updating to reflect may 12 launch; revised flight plan 04/15/09 Adding EVA breakdown; walkthrough 04/23/09 Updating for 5/11 launch target date 04/30/09 Adding STS-400 details from FRR briefing 05/04/09 Adding trajectory data; abort boundaries; STS-400 launch windows Introduction This document is an outgrowth of my original UPI Space Reporter's Handbook, prepared prior to STS-26 for United Press International and updated for several flights thereafter due to popular demand. The current version is prepared for CBS News. As with the original, the goal here is to provide useful information on U.S. and Russian space flights so reporters and producers will not be forced to rely on government or industry public affairs officers at times when it might be difficult to get timely responses. All of these data are available elsewhere, of course, but not necessarily in one place.
    [Show full text]
  • Mario Livio Discusses "Why?"
    Mario Livio discusses "Why?" [00:00:05] Welcome to The Seattle Public Library’s podcasts of author readings and library events. Library podcasts are brought to you by The Seattle Public Library and Foundation. To learn more about our programs and podcasts, visit our web site at w w w dot SPL dot org. To learn how you can help the library foundation support The Seattle Public Library go to foundation dot SPL dot org [00:00:35] Hi everybody. I'm Stesha Brandon. I'm the Literature and Humanities Program Manager here at The Seattle Public Library and welcome to the central library and to tonight's event with Dr. Mario Livio. We would like to thank our authors series sponsor Gary Kunis and the Seattle Times for their generous support for library programs. We are also grateful to The Seattle Public Library Foundation private gifts to the foundation from thousands of donors help the library provide free programs and services that touch the lives of everyone in our community. So if any of you are donors to the Library Foundation thank you so much for your support. Now I am delighted to introduce Mario Livio, an internationally known astrophysicist a best selling author and a popular speaker. Dr. Livio has appeared on The Daily Show 60 Minutes and Nova. He's a Fellow of the American Association for the Advancement of Science. He is the author of many books including the Golden Ratio a highly acclaimed book for which he received the International Pythagoras prize and the Pino prize.
    [Show full text]
  • The Great Math Mystery Mario Livio (1950 - ) Astrophysicist and Writer Astrofísico Y Escritor Astrophysicien Et Écrivain Space Telescope Science Institute
    “How is it possible that mathematics, a product of human thought that is independent of experience, fits so excellently the objects of physical reality?” “¿Cómo es posible que la matemática, un producto del pensamiento humano independiente de la experiencia, se adapte tan admirablemente a los objetos de la realidad?”1 Albert Einstein (1879-1955) “Intelligent people would never say, ‘I don’t care about art, or music. But it is totally okay to say, ‘I hate math.’” The Great Math Mystery Mario Livio (1950 - ) Astrophysicist and writer Astrofísico y escritor Astrophysicien et écrivain Space Telescope Science Institute LIVIO, Mario, “The Great Math Mystery”. This is a Nova Production for WGBF Boston. © 2015 WGBF Educational Foundation. All rights reserved. This program was produced by WGBF, which is solely responsible for its content. Cf.: https://www.youtube.com/watch?v=pPUTrIgdCZI 1 JAMMER, Max, Einstein and Religion, Princeton University Press, 1921, p. 124. The Great Math Mystery Documentary New 2015 HD http://docuwiki.net/index.php?title=T... The Great Math Mystery Documentary New 2015 HD NOVA leads viewers on a mathematical mystery tour –a provocative exploration of math’s astonishing power across the centuries. We discover math’s signature in the swirl of a nautilus shell, the whirlpool of a galaxy, and the spiral in the center of a sunflower. Math was essential to everything from the first wireless radio transmissions to the successful landing of rovers on Mars. But where does math get its power? Astrophysicist and writer Mario Livio, along with a colorful cast of mathematicians, physicists, and engineers, follow math from Pythagoras to Einstein and beyond, all leading to the ultimate riddle: Is math an invention or a discovery? Humankind’s clever trick or the language of the universe? Whether we think we’re good with numbers or not, we all use math in our daily lives.
    [Show full text]
  • Why Math Works So Well
    Fractals, such as this stack of spheres created using 3-D modeling software, are one of the mathematical structures that were invent- ed for abstract reasons yet manage to capture reality. 80 Scientific American, August 2011 © 2011 Scientific American Mario Livio is a theoretical astrophysicist at the Space Telescope Science Institute in Baltimore. He has studied a wide range of cosmic phenomena, ranging from dark energy and super nova explosions to extrasolar planets and accretion onto white dwarfs, neutron stars and black holes. PHILOSOPHY OF SCIENCE Why Math Wo r k s Is math invented or discovered? A leading astrophysicist suggests that the answer to the millennia-old question is both By Mario Livio ost of us take it for granted German physicist Heinrich Hertz detected them. Very that math works—that sci­ few languages are as effective, able to articulate vol­ entists can devise formulas umes’ worth of material so succinctly and with such to describe subatomic events precision. Albert Einstein pondered, “How is it possi­ or that engineers can calcu­ ble that mathematics, a product of human thought late paths for spacecraft. We that is independent of experience, fits so excellently accept the view, initially es­ the objects of physical reality?” poused by Galileo, that mathematics is the language of As a working theoretical astrophysicist, I encoun­ Mscience and expect that its grammar explains experi­ ter the seemingly “unreasonable effectiveness of math­ mental results and even predicts novel phenomena. ematics,” as Nobel laureate physicist Eugene Wigner The power of mathematics, though, is nothing short of called it in 1960, in every step of my job.
    [Show full text]
  • Is Math Invented Or Discovered? a Leading Astrophysicist Suggests That the Answer to the Millennia-Old Question Is Both
    Is math invented or discovered? A leading astrophysicist suggests that the answer to the millennia-old question is both MOST OF US TAKE IT FOR GRANTED that math works--that scientists can devise formulas to describe subatomic events or that engineers can calculate paths for spacecraft. We accept the view, initially espoused by Galileo, that mathematics is the language of science and expect that its grammar explains experimental results and even predicts novel phenomena. The power of mathematics, though, is nothing short of astonishing. Consider, for example, Scottish physicist James Clerk Maxwell's famed equations: not only do these four expressions summarize all that was known of electromagnetism in the 1860s, they also anticipated the existence of radio waves two decades before German physicist Heinrich Hertz detected them. Very few languages are as effective, able to articulate volumes' worth of material so succinctly and with such precision. Albert Einstein pondered, "How is it possible that mathematics, a product of human thought that is independent of experience, fits so excellently the objects of physical reality?" As a working theoretical astrophysicist, I encounter the seemingly "unreasonable effectiveness of mathematics," as Nobel laureate physicist Eugene Wigner called it in 1960, in every step of my job. Whether I am struggling to understand which progenitor systems produce the stellar explosions known as type Ia supernovae or calculating the fate of Earth when our sun ultimately becomes a red giant, the tools I use and the models I develop are mathematical. The uncanny way that math captures the natural world has fascinated me throughout my career, and about 10 years ago I resolved to look into the issue more deeply.
    [Show full text]
  • 2020 Big Questions Research Guide and Brief
    2020 Big Questions Research Guide and Brief 1 Resolved: Mathematics was discovered, not invented This topic brief was written by Jesse Meyer. Jesse is a two diamond coach, recipient of the Donald Crabtree Service Award, the state of Iowa’s 2015 Coach of the Year, member of the TOC’s PF advisory board, and board member of the Iowa Forensics League. He is currently an assistant coach at Iowa City West High School. He can be reached at [email protected]. 2 Table of Contents Table of Contents 2020 Big Questions Research Guide and Brief ................................................................... 1 Resolved: Mathematics was discovered, not invented .................................................... 2 Table of Contents ............................................................................................................................... 3 Topic Analysis ..................................................................................................................................... 4 Further Reading and Teaching Resources ............................................................................. 11 Sample Affirmative Case .............................................................................................................. 13 Sample Negative Case .................................................................................................................... 18 Affirmative Evidence ..................................................................................................................... 22 Math
    [Show full text]
  • George Gamow and Albert Einstein: Did Einstein Say the Cosmological Constant Was the "Biggest Blunder" He Ever Made in His Life?
    1 George Gamow and Albert Einstein: Did Einstein say the cosmological constant was the "biggest blunder" he ever made in his life? Galina Weinstein1 October 3, 2013 Abstract: In 1956/1970 Gamow wrote that much later, when he was discussing cosmological problems with Einstein, he remarked that the introduction of the cosmological term was the "biggest blunder" he ever made in his life. But the cosmological constant rears its ugly head again and again and again. Apparently, Einstein himself has never used the aperçu "biggest blunder"; nevertheless a vast literature grew up around this notion and associated it with Einstein. The present work is prompted by questions put by Mario Livio in his latest book Brilliant Blunders as to the phrase "biggest blunder": Did Einstein actually say, "biggest blunder"? I show that in 1947 Einstein wrote Lemaitre that he found it "very ugly" indeed that the field law of gravitation should be composed of two logically independent terms (one of which was the cosmological term). Earlier, in spring 1922 Einstein wrote Max Born that he committed "a monumental blunder some time ago". In 1965 Born commented on this letter: "Here Einstein admits that the considerations which led him to the positive-ray experiments were wrong: 'a monumental [capital] blunder'". It is likely that when Einstein met Gamow he formulated his views in his native German, and perhaps he told Gamow that suggesting his cosmological constant was a "blunder". I suggest that, Einstein perhaps told Gamow that the cosmological constant was a "capital blunder" or a "monumental blunder", and Gamow could have embellished Einstein's words to become the famous aperçu "biggest blunder".
    [Show full text]
  • The Golden Ratio and Aesthetics
    The golden ratio and aesthetics © 1997−2009, Millennium Mathematics Project, University of Cambridge. Permission is granted to print and copy this page on paper for non−commercial use. For other uses, including electronic redistribution, please contact us. November 2002 Features The golden ratio and aesthetics by Mario Livio Mario Livio is a scientist and self−proclaimed "art fanatic" who owns many hundreds of art books. Recently, he combined his passions for science and art in two popular books, The Accelerating Universe, which appeared in 2000, and The Golden Ratio, reviewed in this issue of Plus. The former book discusses "beauty" as an essential ingredient in fundamental theories of the universe. The latter discusses the amazing appearances of the peculiar number 1.618... in nature, the arts, and psychology. Here he gives us a taster. The origins of the divine proportion In the Elements, the most influential mathematics textbook ever written, Euclid of Alexandria (ca. 300 BC) defines a proportion derived from a division of a line into what he calls its "extreme and mean ratio." Euclid's definition reads: A straight line is said to have been cut in extreme and mean ratio when, as the whole line is to the greater segment, so is the greater to the lesser. In other words, in the diagram below, point C divides the line in such a way that the ratio of AC to CB is equal to the ratio of AB to AC. Some elementary algebra shows that in this case the ratio of AC to CB is equal to the irrational number 1.618 (precisely half the sum of 1 and the square root of 5).
    [Show full text]
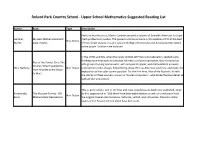
  • Upper School Mathematics Suggested Reading List
    Roland Park Country School - Upper School Mathematics Suggested Reading List Author Book Type Description Every six months or so, Martin Gardner devoted a column of Scientific American to short Gardner, My Best Mathematical and math problems or puzzles. The present volume contains a rich selection of 70 of the best Non-fiction Martin Logic Puzzles of these brain teasers, in some cases including references to new developments related to the puzzle. Solutions are included. In the 1940s and 50s, when the newly minted Jet Propulsion Laboratory needed quick- thinking mathematicians to calculate velocities and plot trajectories, they recruited an Rise of the Rocket Girls: The elite group of young women who, with only pencil, paper, and mathematical prowess, Women Who Propelled Us, Holt, Nathalia Non-fiction transformed rocket design, helped bring about the first American satellites, and made the from Missiles to the Moon exploration of the solar system possible. For the first time, Rise of the Rocket Girls tells to Mars the stories of these women--known as "human computers"--who broke the boundaries of both gender and science. This is, quite simply, one of the best and most popular puzzle book ever published. Since Kordemsky, The Moscow Puzzles: 359 its first appearance in 1956 there have been eight editions as well as translations from Non-fiction Boris Mathematical Recreations the original Russian into Ukrainian, Estonian, Lettish, and Lithuanian. Almost a million copies of the Russian version alone have been sold. For thousands of years mathematicians solved progressively more difficult algebraic equations, until they encountered the quintic equation, which resisted solution for three centuries.
    [Show full text]
  • Reasons in Favor of a Hubble-Lemaître-Slipher's
    S S symmetry Article Reasons in Favor of a Hubble-Lemaître-Slipher’s (HLS) Law Emilio Elizalde Institute of Space Sciences (ICE/CSIC and IEEC), Campus UAB, Carrer de Can Magrans, s/n, 08193 Bellaterra (Barcelona), Spain; [email protected] Received: 27 November 2018; Accepted: 27 December 2018; Published: 2 January 2019 Abstract: Based on historical facts, revisited from a present-day perspective, and on the documented opinions of the scientists involved in the discovery themselves, strong arguments are given in favor of a proposal to add prominent astronomer Vesto Slipher to the suggested addition of Georges Lemaître’s name to Hubble’s law on the expansion of the universe and thus eventually call it the Hubble–Lemaître–Slipher (HLS) law. Keywords: universe expansion; cosmological distances; cosmological velocities; the concept of physical law 1. Introduction To find the origins of astronomy and even of cosmology itself, that is of the knowledge of the universe on a large scale, as a whole, we would have to go far back in the history of humanity. It is generally accepted, however, that modern cosmology, as a science, began to take shape at the beginning of the last century. Before that, the first modern scientists appeared, being Galileo Galilei (1564–1642), according to general consensus, the first of them. As much as we could talk about Galileo, this is not the primary objective of this article, so I will limit myself to refer only to a couple of aspects that do have to do with him. Galileo taught us that science must be based on two fundamental pillars, namely the experimental observation of nature and the scientific theory itself.
    [Show full text]
  • Brilliant Blunders: from Darwin to Einstein - Colossal Mistakes by Great Scientists That Changed Our Understanding of Life and the Universe
    [PDF] Brilliant Blunders: From Darwin To Einstein - Colossal Mistakes By Great Scientists That Changed Our Understanding Of Life And The Universe Mario Livio - download pdf Download Brilliant Blunders: From Darwin To Einstein - Colossal Mistakes By Great Scientists That Changed Our Understanding Of Life And The Universe PDF, Brilliant Blunders: From Darwin To Einstein - Colossal Mistakes By Great Scientists That Changed Our Understanding Of Life And The Universe by Mario Livio Download, Read Brilliant Blunders: From Darwin To Einstein - Colossal Mistakes By Great Scientists That Changed Our Understanding Of Life And The Universe Full Collection Mario Livio, Free Download Brilliant Blunders: From Darwin To Einstein - Colossal Mistakes By Great Scientists That Changed Our Understanding Of Life And The Universe Full Popular Mario Livio, I Was So Mad Brilliant Blunders: From Darwin To Einstein - Colossal Mistakes By Great Scientists That Changed Our Understanding Of Life And The Universe Mario Livio Ebook Download, Free Download Brilliant Blunders: From Darwin To Einstein - Colossal Mistakes By Great Scientists That Changed Our Understanding Of Life And The Universe Full Version Mario Livio, PDF Brilliant Blunders: From Darwin To Einstein - Colossal Mistakes By Great Scientists That Changed Our Understanding Of Life And The Universe Free Download, online pdf Brilliant Blunders: From Darwin To Einstein - Colossal Mistakes By Great Scientists That Changed Our Understanding Of Life And The Universe, pdf download Brilliant Blunders: From Darwin
    [Show full text]
  • The Success of Failure
    The Success of Failure: Perspectives from the Arts, Sciences, Humanities, Education, and Law December 7-8, 2017 Cowin Auditorium, 147 Horace Mann Hall, Teachers College Sponsored by: The Center for Science and Society, Columbia University; The Society of Fellows and Heyman Center for the Humanities, Columbia University; The Institute for Social and Economic Research and Policy, Columbia University; and Teachers College, Columbia University This conference is supported, in part, by The Institute for Social and Economic Research and Policy (ISERP) at Columbia University and the John Templeton Foundation. Introduction: A real failure does not need an excuse. It is an end in itself. – Gertrude Stein We are all familiar with the many bromides teaching us the value of failure on the path to success. It builds character, shows perseverance and dedication, demonstrates willingness to take a risk, and so forth. All perhaps true, but all constrained by a view of failure as a means to an end, an unfortunately necessary obstacle to be overcome. One may learn from failures, but what is mostly meant is that one learns not to do that particular thing again. Failing is fine, especially on someone else’s dime, if you gain some experience to avoid future failures. We take here an alternative view of failure. What about failure as a good? What about the intrinsic value of failure? How about failure that contains valuable data, not just an error message? Failure that is a critical part of the process, not a means to an end? Failure that stands shoulder to shoulder with success? Can there be such a thing as positive failure? Can failure make progress? Can we use failure to improve creativity, education, or behavior? How do we research failure? How do we discover important failures? How do we recognize important failures? This symposium will investigate these and other perspectives on failure across disciplines, searching for commonalities and differences.
    [Show full text]