Mechanical Characterization of the Hard Palate
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
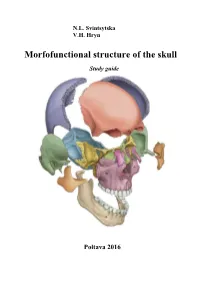
Morfofunctional Structure of the Skull
N.L. Svintsytska V.H. Hryn Morfofunctional structure of the skull Study guide Poltava 2016 Ministry of Public Health of Ukraine Public Institution «Central Methodological Office for Higher Medical Education of MPH of Ukraine» Higher State Educational Establishment of Ukraine «Ukranian Medical Stomatological Academy» N.L. Svintsytska, V.H. Hryn Morfofunctional structure of the skull Study guide Poltava 2016 2 LBC 28.706 UDC 611.714/716 S 24 «Recommended by the Ministry of Health of Ukraine as textbook for English- speaking students of higher educational institutions of the MPH of Ukraine» (minutes of the meeting of the Commission for the organization of training and methodical literature for the persons enrolled in higher medical (pharmaceutical) educational establishments of postgraduate education MPH of Ukraine, from 02.06.2016 №2). Letter of the MPH of Ukraine of 11.07.2016 № 08.01-30/17321 Composed by: N.L. Svintsytska, Associate Professor at the Department of Human Anatomy of Higher State Educational Establishment of Ukraine «Ukrainian Medical Stomatological Academy», PhD in Medicine, Associate Professor V.H. Hryn, Associate Professor at the Department of Human Anatomy of Higher State Educational Establishment of Ukraine «Ukrainian Medical Stomatological Academy», PhD in Medicine, Associate Professor This textbook is intended for undergraduate, postgraduate students and continuing education of health care professionals in a variety of clinical disciplines (medicine, pediatrics, dentistry) as it includes the basic concepts of human anatomy of the skull in adults and newborns. Rewiewed by: O.M. Slobodian, Head of the Department of Anatomy, Topographic Anatomy and Operative Surgery of Higher State Educational Establishment of Ukraine «Bukovinian State Medical University», Doctor of Medical Sciences, Professor M.V. -

Model Keys Unit 1
Model Keys This section will supply you with the keys to several of the models found in the anatomy lab and the learning center. This does not include all the models. After the model keys in this section you will find keys to most of the Nystrom charts. In the anatomy lab there is a reference shelve that contains binders with the keys to most models, torsos and the Nystrom charts. Keys to some of the models are actually attached to the model. Chart keys can also be found either right on the chart or posted next to the chart. Unit 1 Numbered Skull (with colored numbers): g. internal occipital crest a. third molar (inside) b. incisive canal h. clivus (inside) c. infraorbital foramen i. foramen magnum d. infraorbital groove j. jugular foramen e. pterygopalatine fossa k. hypoglossal canal 6. Zygomatic bone l. cerebella fossa (inside) a. zygomaticofacial foramen m. vermain fossa (inside) 7. Sphenoid bone 4. Temporal bone a. medial pterygoid plate a. styloid process b. lateral pterygoid plate b. tympanic part c. lesser wing of sphenoid c. mastoid process (inside) d. mastoid notch d. greater wing of sphenoid 1. Frontal bone e. zygomatic process (inside) a. zygomatic process f. articular tubercle e. chiasmatic groove b. frontal crest (inside) g. stylomastoid foramen (inside) c. orbital part (inside) h. mastoid foramen f. anterior clinoid process d. supraorbital foramen i. external acoustic meatus (inside) e. anterior ethmoidal j. internal acoustic meatus g. posterior clinoid process foramen (inside) (inside) f. posterior ethmoidal k. carotid canal h. hypophyseal fossa foramen l. mandibular fossa (inside) g. -

Prevention of Maxillary Collapse During Sutural Distraction Osteogenesis for Cleft Palate Closure
Prevention of Maxillary Collapse During Sutural Distraction Osteogenesis for Cleft Palate Closure Miroslav S. Gilardino, BSc, MD Department of Experimental Surgery McGill University, Montreal, Quebec, Canada A thesis submitted to McGill University in partial fulfillment of the requirements of the degree of Master' s of Science (Experimental Surgery). July 2005 ~McGill'~-' © Miroslav Sergio Gilardino, 2005 Library and Bibliothèque et 1+1 Archives Canada Archives Canada Published Heritage Direction du Branch Patrimoine de l'édition 395 Wellington Street 395, rue Wellington Ottawa ON K1A ON4 Ottawa ON K1A ON4 Canada Canada Your file Votre référence ISBN: 978-0-494-22726-8 Our file Notre référence ISBN: 978-0-494-22726-8 NOTICE: AVIS: The author has granted a non L'auteur a accordé une licence non exclusive exclusive license allowing Library permettant à la Bibliothèque et Archives and Archives Canada to reproduce, Canada de reproduire, publier, archiver, publish, archive, preserve, conserve, sauvegarder, conserver, transmettre au public communicate to the public by par télécommunication ou par l'Internet, prêter, telecommunication or on the Internet, distribuer et vendre des thèses partout dans loan, distribute and sell theses le monde, à des fins commerciales ou autres, worldwide, for commercial or non sur support microforme, papier, électronique commercial purposes, in microform, et/ou autres formats. paper, electronic and/or any other formats. The author retains copyright L'auteur conserve la propriété du droit d'auteur ownership and moral rights in et des droits moraux qui protège cette thèse. this thesis. Neither the thesis Ni la thèse ni des extraits substantiels de nor substantial extracts from it celle-ci ne doivent être imprimés ou autrement may be printed or otherwise reproduits sans son autorisation. -

Skull Joints
Svintsytska N.L. Hryn V.H. Kovalchuk O.І. MORPHOFUNCTIONAL CHARACTERISTIC OF THE SKULL WITH A CLINICAL ASPECT Study guide Poltava 2020 MINISTRY OF PUBLIC HEALTH OF UKRAINE UKRANIAN MEDICAL STOMATOLOGICAL ACADEMY Nataliya L. Svintsytska, Volodymyr H. Hryn, Oleksandr I. Kovalchuk MORPHOFUNCTIONAL CHARACTERISTIC OF THE SKULL WITH A CLINICAL ASPECT Study guide Poltava 2020 2 UDC 616.714:612 "Recommended by the Academic Council of the Ukrainian Medical Stomatological Academy as a study guide for foreign students receiving higher master's degrees, studying in the specialties 221"Stomatology", 222" Medicine "in higher educational institutions of of the Ministry of Health of Ukraine." Minutes of the meeting of the Academic Council of the Ukrainian Medical Stomatological Academy from 11.03.2020 №8. Composed by: Svintsytska N.L., Associate Professor at the Department of Human Anatomy of Ukrainian Medical Stomatological Academy, PhD in Medicine, Associate Professor Hryn V.H., Associate Professor at the Department of Human Anatomy of Ukrainian Medical Stomatological Academy, PhD in Medicine, Associate Professor Kovalchuk O.І., Head of the Department of Аnatomy and Pathological Physiology of Educational and Scientific Center "Institute of Biology and Medicine" of Taras Shevchenko National University of Kyiv, Doctor of Medical Sciences, Professor Study guide for foreign students of higher medical educational institutions оf Ukraine in Specialties – 222 «Medicine» та 221 «Stomatology». Morphofunctional characteristic of the skull with a clinical aspect. – Poltava, 2020 – 205 р. This guide is intended for undergraduate, postgraduate students and continuing education of health care professionals in a variety of clinical disciplines (medicine, pediatrics, dentistry) as it includes the basic concepts of human anatomy of the skull in adults and newborns. -

Exercises: Refining Cranial Palpation Skills
Exercises.qxd 24/03/05 2:05 PM Page 51 51 Exercises: refining cranial palpation skills Exercise 1 To enhance awareness of CHAPTER CONTENTS palpated inherent tissue sensation Exercise 1 To enhance awareness of palpated inherent tissue sensation 51 Time suggested 10 minutes Exercise 2 To enhance bilateral perception of Frymann (1963) suggests that you sit at a table palpated tissue sensation 52 opposite a partner, one of whose arms rests on the table, flexor surface upwards. This arm Exercise 3 To enhance perception of subtle should be totally relaxed. Place a hand onto sensations in neurally connected areas 52 that forearm with attention focused on what the Exercise 4 To discriminate between palpated palmar surfaces of the fingers are feeling. The sensations deriving from indirectly related other hand should lie on the firm table surface areas 52 in order to provide a contrast reference as the living tissue is palpated, distinguishing a Exercise 5 To discriminate between various region in motion from one without motion. sensations deriving from a palpated Your elbows should rest on the table so that no pulsation 52 stress builds up in the arm or shoulders. Exercise 6 Global suture palpation 53 With eyes closed, concentration should then be projected into what the fingers are feeling, Exercises 7a–7e Static (passive and kinetic) attuning to the arm surface. Gradually, focus cranial suture palpation exercises – supine, should be brought to the deeper tissues under seated and sidelying 57 the skin as well, and finally to the underlying Exercise 8 Cranial vault palpation for cranial bone. motion 61 When structure has been well noted, the function of the tissues should be considered. -

FIPAT-TA2-Part-2.Pdf
TERMINOLOGIA ANATOMICA Second Edition (2.06) International Anatomical Terminology FIPAT The Federative International Programme for Anatomical Terminology A programme of the International Federation of Associations of Anatomists (IFAA) TA2, PART II Contents: Systemata musculoskeletalia Musculoskeletal systems Caput II: Ossa Chapter 2: Bones Caput III: Juncturae Chapter 3: Joints Caput IV: Systema musculare Chapter 4: Muscular system Bibliographic Reference Citation: FIPAT. Terminologia Anatomica. 2nd ed. FIPAT.library.dal.ca. Federative International Programme for Anatomical Terminology, 2019 Published pending approval by the General Assembly at the next Congress of IFAA (2019) Creative Commons License: The publication of Terminologia Anatomica is under a Creative Commons Attribution-NoDerivatives 4.0 International (CC BY-ND 4.0) license The individual terms in this terminology are within the public domain. Statements about terms being part of this international standard terminology should use the above bibliographic reference to cite this terminology. The unaltered PDF files of this terminology may be freely copied and distributed by users. IFAA member societies are authorized to publish translations of this terminology. Authors of other works that might be considered derivative should write to the Chair of FIPAT for permission to publish a derivative work. Caput II: OSSA Chapter 2: BONES Latin term Latin synonym UK English US English English synonym Other 351 Systemata Musculoskeletal Musculoskeletal musculoskeletalia systems systems -

The Palatomaxillary Suture Revisited: a Histological and Immunohistochemical Study Using Human Fetuses
Okajimas Folia Anat.Fetal Jpn., palatomaxillary 94(2): 65–74, August,suture 201765 The palatomaxillary suture revisited: A histological and immunohistochemical study using human fetuses By Ji Hyun KIM1, Masahito YAMAMOTO2, Hiroshi ABE3, Gen MURAKAMI2, 4, Shunichi SHIBATA5, Jose Francisco RODRÍGUEZ-VÁZQUEZ6, Shin-ichi ABE2 1Department of Anatomy, Seonam University College of Medicine, 439 Chunhyang-ro, Namwon, 55724, Korea 2Department of Anatomy, Tokyo Dental College, 2-9-18, Misaki-cho, Chiyoda-ku, Tokyo 101-0061, Japan 3Department of Anatomy, Akita University School of Medicine, 1-1-1, Hondo, Akita, 010-8543, Japan 4Division of Internal Medicine, Iwamizawa Asuka Hospital, 297-13, Iwamizawa, 068-0833, Japan 5Department of Maxillofacial Anatomy, Graduate School of Tokyo Medical and Dental University, 1-5-45, Yushima, Bunkyo-ku, Tokyo, 113-8510, Japan 6Department of Anatomy and Human embryology, Institute of Embryology, Faculty of Medicine, Complutense University, Madrid, 28040, Spain –Received for Publication, May 9, 2017– Key Words: Palatomaxillary suture, transverse palatine fissure, palatine aponeurosis, maxilla, human fetuses Summary: In human fetuses, the palatine process of the maxilla is attached to the inferior aspect of the horizontal plate of the palatine bone (HPPB). The fetal palatomaxillary suture is so long that it extends along the anteroposterior axis rather than along the transverse axis. The double layered bony palate disappears in childhood and the transverse suture is formed. To better understand the development of the double layered bone palate, we examined histological sections obtained from 25 fetuses of gestational age 9–11, 16–18 and 30 weeks. The double layered palate was seen in all of the specimens exam- ined. -

1 Normal and Abnormal Craniofacial Structures
PART Normal and Abnormal 1 Craniofacial Structures CHAPTER 1 Anatomy and Physiology CHAPTER 2 Genetics and Patterns of Inheritance CHAPTER 3 Clefts of the Lip and Palate CHAPTER 4 Dysmorphology and Craniofacial Syndromes CHAPTER 5 Facial, Oral, and Pharyngeal Anomalies CHAPTER 6 Dental Anomalies CHAPTER 7 Early Feeding Problems 1 © Jones & Bartlett Learning, LLC. NOT FOR SALE OR DISTRIBUTION 9781284149722_CH01_Pass03.indd 1 04/06/18 8:20 AM © Jones & Bartlett Learning, LLC. NOT FOR SALE OR DISTRIBUTION 9781284149722_CH01_Pass03.indd 2 04/06/18 8:20 AM CHAPTER 1 Anatomy and Physiology CHAPTER OUTLINE INTRODUCTION Muscles of the Velopharyngeal Valve Velopharyngeal Motor and Sensory Innervation ANATOMY Variations in Velopharyngeal Closure Craniofacial Structures Patterns of Velopharyngeal Closure Craniofacial Bones and Sutures Pneumatic versus Nonpneumatic Activities Ear Timing of Closure Nose and Nasal Cavity Height of Closure Lips Firmness of Closure Intraoral Structures Effect of Rate and Fatigue Tongue Changes with Growth and Age Faucial Pillars, Tonsils, and Oropharyngeal Subsystems of Speech: Putting It All Isthmus Hard Palate Together Velum Respiration Uvula Phonation Prosody Pharyngeal Structures Resonance and Velopharyngeal Function Pharynx Articulation Eustachian Tube Subsystems as “Team Players” PHYSIOLOGY Summary Velopharyngeal Valve For Review and Discussion Velar Movement Lateral Pharyngeal Wall Movement References Posterior Pharyngeal Wall Movement 3 © Jones & Bartlett Learning, LLC. NOT FOR SALE OR DISTRIBUTION 9781284149722_CH01_Pass03.indd 3 04/06/18 8:20 AM 4 Chapter 1 Anatomy and Physiology INTRODUCTION The nasal, oral, and pharyngeal structures are all very important for normal speech and resonance. Unfortu- nately, these are the structures that are commonly affected by cleft lip and palate and other craniofacial anom- alies. -

Anatomy for Anaesthetists
AFAA01 11/11/03 13:38 Page i Anatomy for Anaesthetists .. This page intentionally left blank AFAA01 11/11/03 13:38 Page iii ANATOMY FOR ANAESTHETISTS HAROLD ELLIS CBE, MA, DM, FRCS, FACS(Hon) Clinical Anatomist, Guy’s King’s and St Thomas’s School of Biomedical Sciences, London Emeritus Professor of Surgery, University of London STANLEY FELDMAN BSc, MB, FRCA Emeritus Professor of Anaesthetics, Charing Cross and Westminster Medical School WILLIAM HARROP-GRIFFITHS MA, MB, BS, FRCA Consultant Anaesthetist, St Mary’s Hospital, Paddington, London with a chapter on the Anatomy of Pain contributed by ANDREW LAWSON FFARCSI, FANZCA, FRCA, MSc Consultant in Anaesthesia and Pain Management, Royal Berkshire Hospital, Reading Eighth edition .. .. AFAA01 11/17/03 10:26 Page iv © 1963, 1969, 1977, 1983, 1988, 1993, 1997, 2004 Library of Congress Cataloging-in-Publication Data by Blackwell Science Ltd Ellis, Harold, 1926– a Blackwell Publishing company Anatomy for anaesthetists / Harold Ellis, Stanley Blackwell Science, Inc., 350 Main Street, Malden, Feldman, William Harrop-Griffiths; with a chapter Massachusetts 02148-5020, USA on the Anatomy of pain contributed by Andrew Blackwell Publishing Ltd, 9600 Garsington Road, Lawson.—8th ed. Oxford OX4 2DQ, UK p. ; cm. Blackwell Science Asia Pty Ltd, 550 Swanston Street, Includes bibliographical references and index. Carlton, Victoria 3053, Australia ISBN 1-4051-0663-8 1. Human anatomy. 2. Anesthesiology. The right of the Author to be identified [DNLM: 1. Anatomy. 2. Anesthesia. as the Author of this Work has been QS 4 E47a 2003] I. Feldman, Stanley A. asserted in accordance with the II. Harrop-Griffiths, William. -

A Chronology of Middle Missouri Plains Village Sites
Smithsonian Institution Scholarly Press smithsonian contributions to zoology • number 627 Smithsonian Institution Scholarly Press TheA Chronology Therian Skull of MiddleA Missouri Lexicon with Plains EmphasisVillage on the OdontocetesSites J. G. Mead and R. E. Fordyce By Craig M. Johnson with contributions by Stanley A. Ahler, Herbert Haas, and Georges Bonani SERIES PUBLICATIONS OF THE SMITHSONIAN INSTITUTION Emphasis upon publication as a means of “diffusing knowledge” was expressed by the first Secretary of the Smithsonian. In his formal plan for the Institution, Joseph Henry outlined a program that included the following statement: “It is proposed to publish a series of reports, giving an account of the new discoveries in science, and of the changes made from year to year in all branches of knowledge.” This theme of basic research has been adhered to through the years by thousands of titles issued in series publications under the Smithsonian imprint, com- mencing with Smithsonian Contributions to Knowledge in 1848 and continuing with the following active series: Smithsonian Contributions to Anthropology Smithsonian Contributions to Botany Smithsonian Contributions in History and Technology Smithsonian Contributions to the Marine Sciences Smithsonian Contributions to Museum Conservation Smithsonian Contributions to Paleobiology Smithsonian Contributions to Zoology In these series, the Institution publishes small papers and full-scale monographs that report on the research and collections of its various museums and bureaus. The Smithsonian Contributions Series are distributed via mailing lists to libraries, universities, and similar institu- tions throughout the world. Manuscripts submitted for series publication are received by the Smithsonian Institution Scholarly Press from authors with direct affilia- tion with the various Smithsonian museums or bureaus and are subject to peer review and review for compliance with manuscript preparation guidelines. -
Changes in the Transverse Dimension of the Nasomaxillary Complex Following Rapid Palatal Expansion – a Post-Retention, CBCT Evaluation
University of Nebraska Medical Center DigitalCommons@UNMC Theses & Dissertations Graduate Studies Fall 12-14-2018 Changes in the Transverse Dimension of the Nasomaxillary Complex Following Rapid Palatal Expansion – a Post-Retention, CBCT Evaluation Allison Schubert University of Nebraska Medical Center Follow this and additional works at: https://digitalcommons.unmc.edu/etd Part of the Orthodontics and Orthodontology Commons, Otolaryngology Commons, and the Radiology Commons Recommended Citation Schubert, Allison, "Changes in the Transverse Dimension of the Nasomaxillary Complex Following Rapid Palatal Expansion – a Post-Retention, CBCT Evaluation" (2018). Theses & Dissertations. 331. https://digitalcommons.unmc.edu/etd/331 This Thesis is brought to you for free and open access by the Graduate Studies at DigitalCommons@UNMC. It has been accepted for inclusion in Theses & Dissertations by an authorized administrator of DigitalCommons@UNMC. For more information, please contact [email protected]. CHANGES IN THE TRANSVERSE DIMENSION OF THE NASOMAXILLARY COMPLEX FOLLOWING RAPID PALATAL EXPANSION – A POST-RETENTION, CBCT EVALUATION By Allison Leigh Schubert Van Vooren A THESIS Presented to the Faculty of the University of Nebraska Graduate College in Partial Fulfillment of Requirements for the Degree of Master of Science Medical Sciences Interdepartmental Area Graduate Program Oral Biology Under the Supervision of Professor Thyagaseely (Sheela) Premaraj University of Nebraska Medical Center Omaha, Nebraska November 2018 Advisory Committee: Peter J. Giannini, D.D.S., M.S. Stanton D. Harn, Ph.D. Sung K. Kim, D.D.S. Sundaralingam (Prem) Premaraj, B.D.S., M.S., Ph.D., FRCD(C) ACKNOWLEDGMENTS I would like to thank Dr. Sheela Premaraj, who spent hours of her personal time reviewing and editing thesis drafts. -

Changes in Human Skull Morphology Across the Agricultural Transition Are Consistent with Softer Diets in Preindustrial Farming Groups
Changes in human skull morphology across the agricultural transition are consistent with softer diets in preindustrial farming groups David C. Katza,b,1, Mark N. Grotea, and Timothy D. Weavera aDepartment of Anthropology, University of California, Davis, CA 95616; and bDepartment of Cell Biology & Anatomy, University of Calgary, Calgary, AB T2N 4N1, Canada Edited by Clark Spencer Larsen, The Ohio State University, Columbus, OH, and approved June 19, 2017 (received for review February 14, 2017) Agricultural foods and technologies are thought to have eased the differences in mode of subsistence (22, 23). Due to the complex- mechanical demands of diet—how often or how hard one had to ities of characterizing high-dimensional phenotypes in structured chew—in human populations worldwide. Some evidence suggests samples, each observed variable (shape, diet, genetic data, or a correspondingly worldwide changes in skull shape and form across proxy for it) is typically transformed from its original units to a the agricultural transition, although these changes have proved dif- matrix of pairwise distances between populations. The correlation ficult to characterize at a global scale. Here, adapting a quantitative between shape and diet distances, after accounting for population genetics mixed model for complex phenotypes, we quantify the in- history and structure, becomes the focus of the inquiry. fluence of diet on global human skull shape and form. We detect However, the essential units of morphology are shape, form, and modest directional differences between foragers and farmers. The size, not pairwise distances. The beauty of statistical shape analysis effects are consistent with softer diets in preindustrial farming is its potential to quantify and concretely represent morphological groups and are most pronounced and reliably directional when the differences in morphological units.