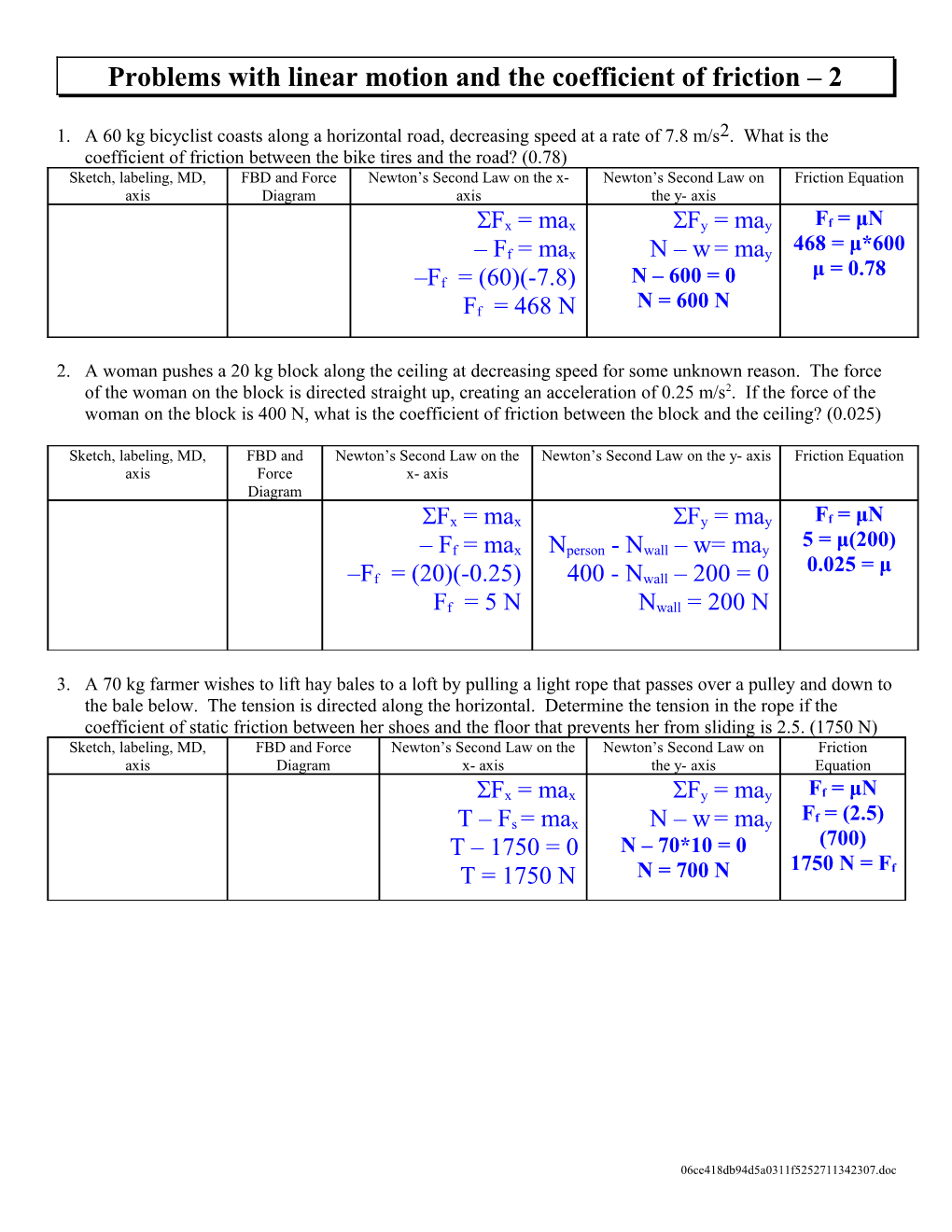
Problems with Linear Motion and the Coefficient of Friction 2

Problems with linear motion and the coefficient of friction – 2

1. A 60 kg bicyclist coasts along a horizontal road, decreasing speed at a rate of 7.8 m/s2. What is the coefficient of friction between the bike tires and the road? (0.78) Sketch, labeling, MD, FBD and Force Newton’s Second Law on the x- Newton’s Second Law on Friction Equation axis Diagram axis the y- axis

Fx = max Fy = may Ff = μN – Ff = max N – w = may 468 = μ*600 μ = 0.78 –Ff = (60)(-7.8) N – 600 = 0 Ff = 468 N N = 600 N

2. A woman pushes a 20 kg block along the ceiling at decreasing speed for some unknown reason. The force of the woman on the block is directed straight up, creating an acceleration of 0.25 m/s2. If the force of the woman on the block is 400 N, what is the coefficient of friction between the block and the ceiling? (0.025)

Sketch, labeling, MD, FBD and Newton’s Second Law on the Newton’s Second Law on the y- axis Friction Equation axis Force x- axis Diagram

Fx = max Fy = may Ff = μN – Ff = max Nperson - Nwall – w= may 5 = μ(200) 0.025 = μ –Ff = (20)(-0.25) 400 - Nwall – 200 = 0 Ff = 5 N Nwall = 200 N

3. A 70 kg farmer wishes to lift hay bales to a loft by pulling a light rope that passes over a pulley and down to the bale below. The tension is directed along the horizontal. Determine the tension in the rope if the coefficient of static friction between her shoes and the floor that prevents her from sliding is 2.5. (1750 N) Sketch, labeling, MD, FBD and Force Newton’s Second Law on the Newton’s Second Law on Friction axis Diagram x- axis the y- axis Equation

Fx = max Fy = may Ff = μN T – Fs = max N – w = may Ff = (2.5) T – 1750 = 0 N – 70*10 = 0 (700) 1750 N = Ff T = 1750 N N = 700 N

06ce418db94d5a0311f5252711342307.doc 4. A 70 kg farmer wishes to lift hay bales to a loft by pulling a light rope that passes over a pulley and down to the 100 kg bale below. The tension is along the horizontal. Determine the minimum coefficient of static friction between her shoes and the loft floor that will prevent her from sliding across the surface while lifting the bale at constant speed. (HINT: Find the tension using the hanging mass.) (1.43) Sketch, labeling, MD, FBD and Force Newton’s Second Newton’s Second Law on the y- Friction Equation axis Diagram Law on the x- axis axis

Fx = max Fy = may T – Fs = max N – w = may 1000 – Fs = 0 N – 70*10 = 0 N = 700 N Ff = μN Fs = 1000 N 1000 = μ * 700 Other system: 1.43 = μ Fy = may T – w = may T – 100*10 = 0 T = 1000 N

5. The largest flowers in the world are the Rafflesia arnoldii, found in Malaysia. A single flower is almost a meter across and has a mass up to 11.0 kg. Suppose you cut off a single flower and drag it along the flat ground. If the coefficient of kinetic friction between the flower and the ground is 0.39, what is the magnitude of the frictional force that must be overcome? (42.9 N) Sketch, labeling, MD, FBD and Force Newton’s Second Law on the x- Newton’s Second Law on Friction Equation axis Diagram axis the y- axis

Fy = may Ff = μN Ff = N – w = may N – 11*10 = 0 0.39*110 N = 110 N Ff = 39N

06ce418db94d5a0311f5252711342307.doc 6. Robert Galstyan, from Armenia, pulled two couple railway wagons a distance of 7m using his teeth. The total mass of the wagons was about 2.20 x 105 kg. Of course, his job was made easier by the fact that the wheels were free to roll. Suppose the wheels are blocked and the coefficient of static friction between the rails and the sliding wheels is 0.220. What would be the magnitude of the minimum force needed to move the wagons from rest? Assume that the track is horizontal. (484,000 N) Sketch, labeling, MD, FBD and Force Newton’s Second Law on Newton’s Second Law on the Friction Equation axis Diagram the x- axis y- axis

Fx = max Fy = may Ff = μN Ff = (0.22) T – Ff = max N – w = may 6 5 N – 2.2x 105*10 = 0 ( 2.2x 10 ) T – 4.84 x 10 = 5 6 Ff = 4.84 x 10 2.2x 105 N = 2.2x 10 N (0) N T = 4.84 x 105 N

7. A blue whale with a mass of 1.90 x 105 kg was caught in 1947. What is the magnitude of the minimum force needed to move the whale along a horizontal ramp if the coefficient of static friction between the ramp’s surface and the whale is 0.460? (874,000 N)

Sketch, labeling, FBD and Newton’s Second Law on the Newton’s Second Law on the y- Friction Equation MD, axis Force Diagram x- axis axis

Fx = max Fy = may Ff = μN N – Ff = max N – w = may Ff = (0.46)( 1.9 x 6 5 N – 1.9x 105*10 = 0 10 ) N – 8.74 x 10 = 0 5 6 Ff = 8.74 x 10 N T = 8.74 x 105 N N = 1.9x 10 N

8. The heaviest train ever pulled by a single engine was over 2 km long. Suppose a force of 1.13 x 108 N is needed to overcome static friction in the train’s wheels. If the coefficient of static friction is 0.741, what is the train’s mass? (1.53 x 107 kg) Sketch, labeling, FBD and Newton’s Second Law on the Newton’s Second Law on the y- Friction Equation MD, axis Force Diagram x- axis axis

Fx = max Fy = may Ff = μN 1.13 x 108 = N – Ff = max N – w = may 8 1.525 x 108 – m*10 = 0 (0.741)( N) N – 1.13 x 10 = 0 8 7 N = 1.525 x 10 N N = 1.13 x 108 N m = 1.525 x 10 kg

06ce418db94d5a0311f5252711342307.doc