A Survey on Latent Tree Models and Applications
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Development of Anderson Road Quarry Site Site Formation and Associated Infrastructure Works
CB(1)876/15-16(01) Legislative Council Panel on Development Development of Anderson Road Quarry Site Site Formation and Associated Infrastructure Works Supplementary Information Introduction Among the follow-up actions of the Legislative Council (LegCo) Panel on Development, Members requested the Government to provide supplementary information about the traffic impact assessment (TIA) and proposed improvement measures for the site formation and associated infrastructure works of the Anderson Road Quarry (ARQ) site. The Civil Engineering and Development Department (CEDD) commenced the site investigation and detailed design study for the development of ARQ site on 18 July 2014, and further reviewed the TIA undertaken at the previous feasibility study stage. CEDD subsequently presented the updated TIA findings and the associated improvement measures to the Kwun Tong District Council (DC) in the first half of 2015. Traffic Impact According to the findings of the TIA report under the “Development of Anderson Road Quarry site – detailed design and site investigations”, the ARQ site development will generate about 840 passenger car units/hour of traffic flow during morning peak hours. As the proposed residential areas will be located mainly in southeast of the development site, it is anticipated that about 70% of the traffic will use the eastern road access connecting Po Lam Road, Sau Mau Ping Road and Tseung Kwan O Road. The remaining 30% will use the access to On Sau Road connecting Clear Water Bay Road and New Clear Water Bay Road. The impact of additional traffic flows to local major roads and junctions arising from the proposed development are set out at Table. -

Wong Tai Sin District(Open in New Window)
District : Wong Tai Sin Recommended District Council Constituency Areas +/- % of Population Estimated Quota Code Recommended Name Boundary Description Major Estates/Areas Population (17,194) H01 Lung Tsui 15,391 -10.49% N Lung Cheung Road 1. LOWER WONG TAI SIN (II) ESTATE (PART) : NE Po Kong Village Road Lung Chi House E Po Kong Village Road Lung Fai House SE Choi Hung Road Lung Gut House Lung Hing House S Shatin Pass Road, Tung Tau Tsuen Road Lung Kwong House SW Ching Tak Street Lung Lok House Lung On House W Ching Tak Street Lung Shing House NW Ching Tak Street, Lung Cheung Road Lung Wai House 2. WONG TAI SIN DISCIPLINED SERVICES QUARTERS H02 Lung Kai 18,003 +4.71% N Tung Tau Tsuen Road 1. KAI TAK GARDEN 2. LOWER WONG TAI SIN (I) ESTATE NE Shatin Pass Road E Choi Hung Road, Shatin Pass Road SE Choi Hung Road S Choi Hung Road, Tai Shing Street SW Tai Shing Street W Tung Tau Tsuen Road NW Tung Tau Tsuen Road H1 District : Wong Tai Sin Recommended District Council Constituency Areas +/- % of Population Estimated Quota Code Recommended Name Boundary Description Major Estates/Areas Population (17,194) H03 Lung Sheung 20,918 +21.66% N Ngan Chuk Lane 1. LOWER WONG TAI SIN (II) ESTATE (PART) : NE Nga Chuk Street, Wong Tai Sin Road Lung Cheung House E Shatin Pass Road, Ying Fung Lane Lung Fook House SE Ching Tak Street, Lung Cheung Road Lung Hei House Lung Moon House S Fung Mo Street, Tung Tau Tsuen Road Lung Tai House SW Fung Mo Street Lung Wo House 2. -

G.N. (E.) 102 of 2014
G.N. (E.) 102 of 2014 ELECTORAL PROCEDURE (RURAL REPRESENTATIVE ELECTION) REGULATION (Cap. 541 sub. leg. L) (Sections 15 and 16 of the Regulation) NOTICE OF NOMINATIONS AND DULY ELECTED CANDIDATES IN UNCONTESTED ELECTIONS 2015 RURAL ORDINARY ELECTION ELECTION OF INDIGENOUS INHABITANT REPRESENTATIVE HANG HAU RURAL COMMITTEE The following candidates are validly nominated for the Indigenous Villages and Composite Indigenous Villages specified below: (Particulars as shown on Nomination Form) Name of Indigenous Name of Candidate Principal Residential Address Village and Composite Indigenous Village FU TAU CHAU YIP,PAK LAM 1/F NO.48 HANG HAU ROAD HA YEUNG LAU,YUK PING NO.4, SIU HANG HAU VILLAGE HA YEUNG VILLAGE CLEAR WATER BAY ROAD SAI KUNG HANG HAU CHEUNG,SHEK G/F, NO.27, HANG HAU VILLAGE KAM TSEUNG KWAN O, SAI KUNG SHING,KING LUN 2/F, NO.67, HANG HAU VILLAGE, ALAN TSEUNG KWAN O. SAI KUNG YAU,WING 2/F NO.39 TIN HA WAN VILLAGE CHUNG PAUL TSEUNG KWAN O MANG KUNG UK HUNG,TIN SUNG 2/F, NO.55, HUNG UK VILLAGE MANG KUNG UK, SAI KUNG, HONG KONG SHING,KUEN 1/F 60 CLEARWATERBAY ROAD WAI FUNG SUM VILLAGE MANG KUNG UK SAI KUNG HONG KONG SING,HEUNG G/F NO 29B O PUI VILLAGE MANG MAN KUNG UK CLEAR WATER BAY KOWLOOM, HONG KONG SING,HON KEUNG 5 WO TONG KWONG, MANG KUNG UK VILLAGE, CLEAR WATER BAY ROAD, HANG HAU, KOWLOON, HONG KONG YU,YUK MING 2/F. 12. YU UK VILL. MAN KUNG UK RD. CLEAR WATER BAY RD. KLN MAU WU TSAI YUEN,SIU 2/F, 5 MAU WU TSAI VILLAGE, PO LAM CHEONG SOUTH ROAD, SAI KUNG, NEW TERRITORIES, HONG KONG TAI HANG HAU LEUNG,WAI NO.80 TAI HANG HAU VILLAGE HUNG GRANY CLEAR WATER BAY SAI KUNG TAI WAN TAU LAU,WAI FLAT C 4/F HARBOUR COURT NO.18 CHEUNG PETER KAI YUEN TERRACE NORTH POINT HONG KONG TIN HA WAN SIT,KAM FUN 2/F NO.7 TIN HA WAN VILLAGE, TSEUNG KWAN O, HONG KONG YAU YUE WAN CHUNG,LIN HI G/F 77 YAU YUE WAN VILLAGE HANG HAU SAI KUNG 2. -

Annex Compulsory Testing Notices Issued by the Secretary for Food
Annex Compulsory Testing Notices issued by the Secretary for Food and Health on December 30, 2020 Amended List of Specified Premises 1. Hibiscus House, Ma Tau Wai Estate, 9 Shing Tak Street, Kowloon City, Kowloon, Hong Kong 2. David Mansion, 93-103 Woosung Street, Yau Ma Tei, Kowloon, Hong Kong 3. Tung Hoi House, Tai Hang Tung Estate, 88 Tai Hang Tung Road, Shek Kip Mei, Kowloon, Hong Kong 4. Un Mun House, Un Chau Estate, 303 Un Chau Street, Sham Shui Po, Kowloon, Hong Kong 5. Fu Wen House, Fu Cheong Estate, 19 Sai Chuen Road, Sham Shui Po, Kowloon, Hong Kong 6. Cherry House, So Uk Estate, 380 Po On Road, Sham Shui Po, Kowloon, Hong Kong 7. Tao Tak House, Lei Cheng Uk Estate, 10 Fat Tseung Street, Sham Shui Po, Kowloon, Hong Kong 8. Scenic Court, 451-461 Shun Ning Road, Sham Shui Po, Kowloon, Hong Kong 9. Block 11, Rhythm Garden, 242 Choi Hung Road, Wong Tai Sin, Kowloon, Hong Kong 10. Chi Siu House, Choi Wan (I) Estate, 45 Clear Water Bay Road, Wong Tai Sin, Kowloon, Hong Kong 11. Sau Man House, Choi Wan (I) Estate, 45 Clear Water Bay Road, Wong Tai Sin, Kowloon, Hong Kong 12. Kai Fai House, Choi Wan (II) Estate, 55 Clear Water Bay Road, Wong Tai Sin, Kowloon, Hong Kong 13. Ching Yuk House, Tsz Ching Estate, 80 Tsz Wan Shan Road, Wong Tai Sin, Kowloon, Hong Kong 14. Ching Tai House, Tsz Ching Estate, 80 Tsz Wan Shan Road, Wong Tai Sin, Kowloon, Hong Kong 15. -

Dualling of Hiram's Highway Between Clear Water Bay Road and Marina
For discussion PWSC(2015-16)22 (date to be confirmed) ITEM FOR PUBLIC WORKS SUBCOMMITTEE OF FINANCE COMMITTEE HEAD 706 – HIGHWAYS Transport – Roads 703TH – Dualling of Hiram’s Highway between Clear Water Bay Road and Marina Cove and Improvement to Local Access to Ho Chung Members are invited to recommend to the Finance Committee the upgrading of 703TH to Category A at an estimated cost of $1,774.4 million in money-of-the- day prices. PROBLEM The traffic flow in some sections of Hiram’s Highway has exceeded their design capacity, leading to traffic congestion. PROPOSAL 2. The Director of Highways, with the support of the Secretary for Transport and Housing, proposes to upgrade 703TH to Category A at an estimated cost of $1,774.4 million in money-of-the-day (MOD) prices for dualling of Hiram’s Highway between Clear Water Bay Road and Marina Cove and improvement works to local access to Ho Chung. / PROJECT ….. PWSC(2015-16)22 Page 2 PROJECT SCOPE AND NATURE 3. The proposed scope of works under the project includes – (a) provision of an additional two-lane Sai Kung bound carriageway of approximately 720 metres (m) long alongside the existing Hiram’s Highway between Clear Water Bay Road and New Hiram’s Highway, and reconstruction of the existing Kowloon bound carriageway; (b) widening of a section of Hiram’s Highway of approximately 900 m long between Nam Pin Wai roundabout and Pak Wai from a single two-lane carriageway to a dual two-lane carriageway; (c) provision of an approximately 47 m long vehicular bridge-cum-walkway of approximately -

KMB Route No. 91A (Diamond Hill Station to Clear Water Bay / Clear Water Bay to Choi Hung Estate (Hung Ngok House))
Traffic Advice KMB Route No. 91A (Diamond Hill Station to Clear Water Bay / Clear Water Bay to Choi Hung Estate (Hung Ngok House)) Members of public are advised that KMB Route No. 91A will be operated from 19 June 2021 to 29 August 2021. The operating details of the route are as follows: Route: KMB Route No. 91A (Diamond Hill Station to Clear Water Bay / Clear Water Bay to Choi Hung Estate (Hung Ngok House)) Routeing: From Diamond Hill Station via Lung Poon Street, Tai Hom Road, Lung Cheung Road, Clear Water Bay Road, New Clear Water Bay Road, Clear Water Bay Road and Tai Au Mun Road. From Clear Water Bay via Tai Au Mun Road, Clear Water Bay Road, New Clear Water Bay Road, Clear Water Bay Road and Lung Cheung Road. Headways: 60 mins Operating 19 June 2021 to 29 August 2021 (Saturdays, Sundays and Public Hours: Holidays only) From Diamond Hill Station 09:00 a.m. to 12:00 n.n. From Clear Water Bay 03:00 p.m. to 07:00 p.m. Fare: Full Fare: $7.8 Section Fare: $7.2 (from Ta Ku Ling Sun Tsuen to Clear Water Bay / from Pak Hung House to Choi Hung Estate (Hung Ngok House)) Bus Stops: From Diamond Hill Station 1. Lung Poon Street inside Plaza Hollywood 2. Lung Cheung Road outside Ngau Chi Wan Village 3. New Clear Water Bay Road outside Pak Hung House, Choi Wan Estate 4. Clear Water Bay Road near Ta Kwu Ling San Tsuen 5. Clear Water Bay Road near Silverstrand Mart 6. -

Via on King Street, Unnamed Road, Tai Chung Kiu Road, Sha Tin Rural Committee Road and Tai Po Road
L. S. NO. 2 TO GAZETTE NO. 50/2004L.N. 203 of 2004 B1965 Air-Conditioned New Territories Route No. 284 Ravana Garden—Sha Tin Central RAVANA GARDEN to SHA TIN CENTRAL: via On King Street, unnamed road, Tai Chung Kiu Road, Sha Tin Rural Committee Road and Tai Po Road. SHA TIN CENTRAL to RAVANA GARDEN: via Sha Tin Centre Street, Wang Pok Street, Yuen Wo Road, Sha Tin Rural Committee Road, Tai Chung Kiu Road and On King Street. Air-Conditioned New Territories Route No. 285 Bayshore Towers—Heng On (Circular) BAYSHORE TOWERS to HENG ON (CIRCULAR): via On Chun Street, On Yuen Street, Sai Sha Road, Ma On Shan Road, Kam Ying Road, Sai Sha Road, Hang Hong Street, Hang Kam Street, Heng On Bus Terminus, Hang Kam Street, Hang Hong Street, Ma On Shan Road, On Chiu Street and On Chun Street. Special trips are operated from the stop on Kam Ying Road outside Kam Lung Court to Heng On. Air-Conditioned New Territories Route No. 286M Ma On Shan Town Centre—Diamond Hill MTR Station (Circular) MA ON SHAN TOWN CENTRE to DIAMOND HILL MTR STATION (CIRCULAR): via Sai Sha Road, Hang Hong Street, Chung On Estate access road, Chung On Bus Terminus, Chung On Estate access road, Sai Sha Road, roundabout, Hang Fai Street, Ning Tai Road, Po Tai Street, Ning Tai Road, Hang Tai Road, Hang Shun Street, A Kung Kok Street, Shek Mun Interchange, *(Tate’s Cairn Highway), Tate’s Cairn Tunnel, Hammer Hill Road, roundabout, Fung Tak Road, Lung Poon Street, Diamond Hill MTR Station Bus Terminus, Lung Poon Street, Tai Hom Road, Tate’s Cairn Tunnel, Tate’s Cairn Highway, Shek Mun Interchange, A Kung Kok Street, Hang Shun Street, Hang Tai Road, Ning Tai Road, Hang Fai Street, roundabout, Sai Sha Road, On Yuen Street, On Chun Street, On Chiu Street and Sai Sha Road. -

Bank of China (Hong Kong)
Bank of China (Hong Kong) Bank Branch Address 1. Central District Branch 2A Des Voeux Road Central, Hong Kong 2. Prince Edward Branch 774 Nathan Road, Kowloon 3. 194 Cheung Sha Wan Road 194-196 Cheung Sha Wan Road, Sham Shui Po, Branch Kowloon 4. Pak Tai Street Branch 4-6 Pak Tai Street, To Kwa Wan, Kowloon 5. Tsuen Wan Branch 297-299 Sha Tsui Road, Tsuen Wan, New Territories 6. Kwai Chung Road Branch 1009 Kwai Chung Road, Kwai Chung, New Territories 7. Sheung Kwai Chung 7-11 Shek Yi Road, Sheung Kwai Chung, New Branch Territories 8. Ha Kwai Chung Branch 192-194 Hing Fong Road, Kwai Chung, New Territories 9. Fuk Tsun Street Branch 32-40 Fuk Tsun Street, Tai Kok Tsui, Kowloon 10. Kwong Fuk Road Branch 40-50 Kwong Fuk Road, Tai Po Market, New Territories 11. Texaco Road Branch Shop A112, East Asia Gardens, 36 Texaco Road, Tsuen Wan, New Territories 12. Cheung Hong Estate 2 G/F, Commercial Centre, Cheung Hong Estate, Commercial Centre Branch Tsing Yi Island, New Territories 13. Kin Wing Street Branch 24-30 Kin Wing Street, Tuen Mun, New Territories 14. Choi Wan Estate Branch Shop Nos. A317 and A318, 3/F, Choi Wan Shopping Centre Phase II, No. 45 Clear Water Bay Road, Ngau Chi Wan, Kowloon 15. Lung Hang Estate Branch 103 Lung Hang Commercial Centre, Sha Tin, New Territories 16. Lei Cheng Uk Estate Shop 108, Lei Cheng Uk Commercial Centre, Lei Branch Cheng Uk Estate, Kowloon 17. Heng Fa Chuen Branch Shop 205-208, East Wing Shopping Centre, Heng Fa Chuen, Chai Wan, Hong Kong 18. -
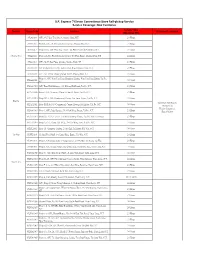
S.F. Express 7-Eleven Convenience Store Self-Pickup Service Service Coverage: New Territories
S.F. Express 7-Eleven Convenience Store Self-pickup Service Service Coverage: New Territories Service Time District Store Code Address Shipment Limitation (Mon-Sun, PH) 852A1003 G/F, 25-27 San Tsoi Street, Sheung Shui, N.T. 24 Hours 852A1005 Shop B, G/F, 76-86 Lung Sum Avenue, Sheung Shui, N.T. 24 Hours 852A1013 Shop 110A, G/F, Ping Hay House, Tai Ping Estate, Sheung Shui, N.T. 24 Hours Sheung Shui 852A1021 Shop 116, Tin Ping Shopping Centre, Tin Ping Estate, Sheung Shiu, NT 24 Hours 852A1016 G/F., No.75 San Fung Avenue, Sheung Shui, NT 24 Hours 852A1020 G/F & Cockloft, No.182 Jockey Club Road, Shueng Shui, N.T. 24 Hours 852A1022 G/F., No. 25 San Cheung Street North, Sheung Shui, N.T. 24 Hours Shop 11, G/F, Wan Tau Tong Shopping Centre, Wan Tau Tong Estate, Tai Po, 852AA1001 24 Hours N.T. 852AA1004 G/F, Tung Fuk Building, 148 Kwong Fuk Road, Tai Po, N.T. 24 Hours 852AA1006 Shop 1, G/F, Greenery Plaza, 3 Chui Yi Street, Tai Po, N.T. 24 Hours 852AA1010 Shop 101 & 109, Commercial Centre, Tai Yuen Estate, Tai Po, N.T. 24 Hours Tai Po Maximum Dimension: 852AA1011 Shop P102 & 103, Commercial Centre, Kwong Fuk Estate, Tai Po, N.T. 24 Hours 36x30x25cm Weight Limitation: 852AA1013 Shop 1, G/F., Jade Garden, No.9 Pak Shing Street, Tai Po, N.T. 24 Hours 5kg or below 852AA1014 Shop No. 227A, Level 2, Tai Wo Shopping Centre, Tai Po, New Territories 24 Hours 852AA1015 Shop A, G/F., Hang Lok Bldg., 2-4 Tai Wing Lane, Tai Po, N.T. -

Recommended District Council Constituency Areas
District : Wong Tai Sin Recommended District Council Constituency Areas +/- % of Population Estimated Quota Code Recommended Name Boundary Description Major Estates/Areas Population (17,282) H01 Lung Tsui 13,080 -24.31 N Lung Cheung Road 1. LOWER WONG TAI SIN (II) ESTATE (PART) : NE Lung Cheung Road, Po Kong Village Road Lung Chi House E Po Kong Village Road Lung Fai House Lung Gut House SE Choi Hung Road Lung Hing House S Choi Hung Road, Shatin Pass Road Lung Kwong House Tung Tau Tsuen Road Lung Lok House Lung On House SW Ching Tak Street Lung Shing House W Ching Tak Street Lung Wai House NW Ching Tak Street, Lung Cheung Road 2. WONG TAI SIN DISCIPLINED SERVICES QUARTERS H02 Lung Ha 13,892 -19.62 N Tung Tau Tsuen Road, Shatin Pass Road 1. LOWER WONG TAI SIN (I) ESTATE NE Shatin Pass Road E Choi Hung Road, Shatin Pass Road SE Choi Hung Road S Choi Hung Road, Tai Shing Street SW Tai Shing Street W Tung Tau Tsuen Road NW Tung Tau Tsuen Road H1 District : Wong Tai Sin Recommended District Council Constituency Areas +/- % of Population Estimated Quota Code Recommended Name Boundary Description Major Estates/Areas Population (17,282) H03 Lung Sheung 20,859 +20.70 N Ma Chai Hang Road, Wong Tai Sin Road 1. LOWER WONG TAI SIN (II) ESTATE (PART) : Choi Chuk Street, Ngan Chuk Lane Lung Cheung House Nga Chuk Street Lung Fook House NE Nga Chuk Street, Wong Tai Sin Road Lung Hei House Lung Moon House E Shatin Pass Road, Ying Fung Lane Lung Tai House Lung Cheung Road Lung Wo House SE Lung Cheung Road, Ching Tak Street 2. -

Business Overview About MTR
Business Overview About MTR MTR is regarded as one of the world’s leading railways for safety, reliability, customer service and cost efficiency. In addition to its Hong Kong, China and international railway operations, the MTR Corporation is involved in a wide range of business activities including the development of residential and commercial properties, property leasing and management, advertising, telecommunication services and international consultancy services. Corporate Strategy MTR is pursuing a new Corporate Strategy, “Transforming the Future”, The MTR Story by more deeply embedding sustainability and Environmental, Social and Governance principles into its businesses and operations The MTR Corporation was established in 1975 as the Mass Transit with the aim of creating more value for all the stakeholders. Railway Corporation with a mission to construct and operate, under prudent commercial principles, an urban metro system to help meet The strategic pillars of the new Corporate Strategy are: Hong Kong’s public transport requirements. The sole shareholder was the Hong Kong Government. The platform columns at To Kwa Wan Station on Tuen Ma Line are decorated with artworks entitled, “Earth Song”, which presents a modern interpretation of the aesthetics of the Song Dynasty, The Company was re-established as the MTR Corporation Limited in June 2000 after the Hong Kong Special Administrative Region illustrating the scenery from day to night and the spring and winter seasons using porcelain clay. Government sold 23% of its issued share capital to private investors Hong Kong Core in an Initial Public Offering. MTR Corporation shares were listed on the Stock Exchange of Hong Kong on 5 October 2000. -

Sewerage at Clear Water Bay Road, Pik Shui Sun Tsuen and West of Sai Kung Town
For discussion PWSC(2012-13)40 on 17 December 2012 ITEM FOR PUBLIC WORKS SUBCOMMITTEE OF FINANCE COMMITTEE Head 704 – DRAINAGE Environmental Protection – Sewerage and sewage treatment 382DS – Sewerage at Clear Water Bay Road, Pik Shui Sun Tsuen and west of Sai Kung town Members are invited to recommend to Finance Committee to increase the approved project estimate of 382DS by $68.4 million from $290.6 million to $359.0 million in money-of-the-day prices. PROBLEM The approved project estimate (APE) of 382DS is not sufficient to cover the cost of works under the project. PROPOSAL 2. The Director of Drainage Services, with the support of the Secretary for the Environment, proposes to increase the APE of 382DS by $68.4 million from $290.6 million to $359.0 million in money-of-the-day (MOD) prices. PROJECT SCOPE AND NATURE 3. In June 2012, the Finance Committee (FC) approved the upgrading of part of 272DS “Port Shelter sewerage, stage 2” and part of 273DS “Port Shelter sewerage, stage 3” to Category A as 382DS at an estimated cost of $290.6 million in MOD prices. The approved scope of 382DS comprises the construction of – /(a) ….. PWSC(2012-13)40 Page 2 (a) about 12.8 kilometres (km) of sewers ranging from 150 millimetres (mm) to 300 mm in diameter for 11 unsewered areas, namely Kap Pin Long, Nam Shan, Pak Kong, San Uk, Sha Kok Mei, Tai Ping Village, Tai Shui Tseng, Wo Tong Kong, Lung Wo Tsuen, Pik Shui Sun Tsuen and in the vicinity of Fei Ngo Shan Road; (b) about 3.6 km of gravity trunk sewers ranging from 225 mm to 450 mm in diameter along Clear Water Bay Road from Shun Chi Street to Razor Hill Road and around Pik Shui Sun Tsuen; (c) one sewage pumping station (SPS) at Pik Shui Sun Tsuen; (d) about 900 metres (m) of twin rising mains ranging from 150 mm to 350 mm in diameter – (i) at Pik Shui Sun Tsuen in association with construction of the SPS in (c) above; (ii) along sections of Clear Water Bay Road near Tseng Lan Shue and Pak Shek Wo; and (e) ancillary works.