DOCSLIB.ORG

Attractor Molecular Signatures and Their Applications for Prognostic Biomarkers Wei-Yi Cheng

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Attractor Molecular Signatures and Their Applications for Prognostic Biomarkers Wei-Yi Cheng Attractor Molecular Signatures and Their Applications for Prognostic Biomarkers Wei-Yi Cheng Submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy of the Graduate School of Arts and Science COLUMBIA UNIVERSITY 2014 c 2013 Wei-Yi Cheng All rights reserved ABSTRACT Attractor Molecular Signatures and Their Applications for Prognostic Biomarkers Wei-Yi Cheng This dissertation presents a novel data mining algorithm identifying molecular sig- natures, called attractor metagenes, from large biological data sets. It also presents a computational model for combining such signatures to create prognostic biomarkers. Us- ing the algorithm on multiple cancer data sets, we identified three such gene co-expression signatures that are present in nearly identical form in different tumor types represent- ing biomolecular events in cancer, namely mitotic chromosomal instability, mesenchymal transition, and lymphocyte infiltration. A comprehensive experimental investigation us- ing mouse xenograft models on the mesenchymal transition attractor metagene showed that the signature was expressed in the human cancer cells, but not in the mouse stroma. The attractor metagenes were used to build the winning model of a breast cancer prog- nosis challenge. When applied on larger data sets from 12 different cancer types from The Cancer Genome Atlas \Pan-Cancer" project, the algorithm identified additional pan-cancer molecular signatures, some of which involve methylation sites, microRNA expression, and protein activity. Contents List of Figures iv List of Tables vi 1 Introduction 1 1.1 Background . 1 1.2 Previous Work on Identifying Cancer-Related Gene Signatures . 3 1.3 Contributions of the Thesis . 9 2 Attractor Metagenes 11 2.1 Derivation of an Attractor Metagene . 12 2.2 Derivation of a Genomically Co-localized Attractor Metagene . 16 2.3 Derivation of Consensus Attractor Signatures . 17 2.4 Evaluating the Significance of an Attractor Signature . 19 2.5 Choice of Parameters in the Iterative Algorithm . 20 2.6 Comparison with Other Unsupervised Algorithms . 23 2.7 Implementation Complexity . 26 3 Pan-Cancer Attractor Signatures 30 3.1 TCGA Pan-Cancer Project . 31 3.2 18 Pan-Cancer Molecular Signatures . 32 3.3 MES mRNA Signature . 36 3.4 Mitotic CIN mRNA Signature . 37 i 3.5 M+, M− Methylation and LYM mRNA Signature . 40 3.6 END mRNA Signature . 45 3.7 Chr8q24.3 Amplicon mRNA Signature . 46 3.8 Other Pan-Cancer Signatures . 49 4 Further Investigation on the Mesenchymal Transition Signature 53 4.1 MES Signature and Tumor Invasiveness . 53 4.2 MES Signature and Recurrence in Glioblastoma . 54 4.3 Association Between MES Signature and CD44 . 60 4.4 Comparing the MES Signature with Other Mesenchymal Subtypes in Glioma 62 4.5 Source of MES Signature . 63 5 Predicting Breast Cancer Prognosis Using Attractor Signatures 70 5.1 The Sage Bionetworks-DREAM BCC . 71 5.2 Identifying Prognostic Features . 73 5.2.1 Mitotic CIN Signature . 75 5.2.2 MES Signature . 76 5.2.3 LYM Signature . 77 5.2.4 FGD3 -SUSD3 Metagene . 78 5.2.5 Other Breast Cancer-Specific Features . 80 5.3 Building an Ensemble Prognostic Model . 82 5.3.1 Derivation of Features . 82 5.3.2 Building Prognostic Models . 84 5.3.3 Combination of Predictions . 87 5.3.4 Combination of OS- and DS-based Predictions . 88 5.4 Performance of the Prognostic Model in the BCC . 88 5.5 Comparison with Random Gene Expression Signatures . 90 6 Conclusions and Future Work 92 6.1 Building Genomic Assays for Cancer Prognosis Using Attractor Signatures 94 ii 6.2 Integrating Attractor Signatures with Additional Information for Biological Discovery . 96 6.3 Comparing Attractor Signatures Identified in Normal Tissues with Pan-Cancer Attractor Signatures . 96 Bibliography 99 A Mutual Information Estimation 111 B Data Sets and Pre-processing 112 B.1 Data Sets Used in This Dissertation . 112 B.2 Pre-processing of Data Sets . 113 B.2.1 Pre-processing of Gene Expression Microarray Data Sets . 113 B.2.2 Pre-processing of RNASeq and miRNASeq Data Sets . 113 B.2.3 Pre-processing of DNA Methylation and RPPA Data Sets . 113 B.2.4 Clustering Attractors and Creating Consensus Molecular Signatures in Pancan 12 Data Sets . 114 C Supplementary Tables 115 iii List of Figures 2.1 Convergence process of an attractor. 15 2.2 Top 5 attractor clusters found in 6 cancer data sets. 28 2.3 Exponent α and the strength of an attractor. 29 3.1 Scatter plots between ESTIMATE stromal scores and MES signature. 38 3.2 Box plots connecting CIN signature with histological tumor grade. 40 3.3 Scatter plots connecting the LYM, M+ and M- signature in 12 cancer types. 41 3.4 Pan-cancer correlation between LYM signature and leukocyte percentage. 42 3.5 Scatter plots demonstrating the pan-cancer similarity of the LYM feature to ESTIMATE immune score. 43 3.6 Scatter plots demonstrating the pan-cancer association among the LYM feature, M-feature, and the miR-142 microRNA expression. 44 3.7 Scatter plots demonstrating the pan-cancer association between MES and END feature. 47 3.8 Co-amplification of the chr8q24.3 amplicon signature in three TCGA data sets. 48 3.9 DLK1 -DIO3 cluster of ncRNA. 50 4.1 Scatter plot showing the association between MES signature and time to tumor recurrence. 55 4.2 Heat map of the top 10 genes of the MES signature in glioblastoma. 56 iv 4.3 Kaplan-Meier curves comparing samples with high vs. low levels of the MES signature . 58 4.4 Scatter plot showing association between CD44 and MES signature . 59 4.5 Scatter plots showing the association among MES signature, COL11A1, and SNAI2................................... 65 4.6 Scatter plots showing the association among MES signature, COL11A1, and SNAI2 in human and mouse cells. 66 4.7 Heat map showing differentially expressed human and mouse genes. 68 5.1 Kaplan-Meier cumulative survival curves of breast cancer patients over a 15-year period on the basis of the mitotic CIN signature expression . 76 5.2 Kaplan-Meier cumulative survival curves of breast cancer patients over a 15-year period on the basis of the LYM signature expression . 78 5.3 FGD3 -SUSD3 metagene. 79 5.4 Schematic of model development. 83 5.5 Kaplan-Meier cumulative survival curve of the final ensemble model. 89 v List of Tables 3.1 Listing of the 18 attractor signatures . 34 4.1 Top genes in terms of the rank sum for the prolonged time to recurrence. 57 4.2 Top differentially expressed genes in GBM versus lower grade glioma. 61 4.3 Cox regression using MES feature or subtypes in GBM as covariates. 63 5.1 Individual gene expression and survival. 74 5.2 Molecular features used in the model . 81 5.3 Cox proportional hazards model trained on molecular and clinical features on the basis of AIC. 86 5.4 Cox proportional hazards models trained on empirically selected features 87 5.5 CIs of the CIN feature and meta-PCNA index in four breast cancer data sets. 90 C.1 Top 100 genes of the mitotic CIN signature . 115 C.2 Top 100 genes of the MES signature . 115 C.3 Top 168 genes with consensus MI > 0:5 in the LYM signature . 116 C.4 Top 27 methylation sites with consensus MI > 0:5 in the M− signature . 117 C.5 Top 27 genes with consensus MI > 0:5 in the END signature . 117 C.6 Association of MES signature with tumor stage . 118 vi Acknowledgements I would like to thank Tai-Hsien Ou Yang for help with some of the work in this thesis, Linda Raynes for editing, Hsu-Cheng Huang, Wen-Chiang Hong, Chien-Yu Lin, Ching- Ting Chen, Ping-Chien Wu, and Yen-Yi Chen for their support and company. Most importantly, I wish to thank my advisor, Professor Dimitris Anastassiou, for being an inspiring mentor, a supportive supervisor, and an enthusiastic project leader, without whom I would have never completed this work. vii To my parents Yi-Chang Cheng and Wei-Ping Tsai, my brother Wei-Chun Cheng and to my wife Tsai-Wei Chiu viii Chapter 1 Introduction The goal of this thesis is to introduce several molecular signatures that are identified by a novel data mining algorithm across multiple genome-scale biomedical data sets, which we called attractor metagenes. These attractor molecular signatures were found in nearly identical form in multiple data sets of different cancer types, and therefore we hypothezie that they represent the unifying characteristics in cancer. The \pan-cancer" molecular signatures provided insights in generating novel hypotheses for cancer biology and helped build models used to predict clinical phenotypes. 1.1 Background Cancer is prevailingly viewed as a process of clonal evolution. In 1976, Peter Nowell proposed that tumor initiation occurs by an induced change in a single, previously normal cell, making the cell neoplastic and providing it with a selective growth advantage over adjacent normal cells [1]. This neoplastic proliferation then proceeds, allowing sequential selection of more aggressive sublines. As evidenced by its pathological manifestations, cancer is also recognized as many diseases, differing in each patient, which progressively evolve through interplay with a changing environment. The unique nature of cancer 1 demands a more individually-tailored treatment − one that identifies the characteristics of a tumor and adopts therapy accordingly. Even before the term \personalized medicine" emerged, oncologists focused on identifying histological or molecular markers in tumor specimens from individual patients which were associated with prognosis or responses to a specific treatment. Ever since the Human Genome Project [2] was completed, the information of individ- ual genetic, genomic, epigenomic, and proteomic characteristics gradually increased their influence on medical decisions, practices, and products.
Load more

Recommended publications
  • Case Report a Fetus with Kabuki Syndrome 2 Detected by Chromosomal Microarray Analysis
    Int J Clin Exp Pathol 2020;13(2):302-306 www.ijcep.com /ISSN:1936-2625/IJCEP0104334 Case Report A fetus with Kabuki syndrome 2 detected by chromosomal microarray analysis Chen-Zhao Lin1, Bi-Ru Qi1, Jian-Su Hu2, Xiu-Qiong Huang3 Departments of 1Obstetrics and Gynecology, 2Ultrasound, 3Laboratory Medicine, Fuzhou Municipal First Hospital Affiliated to Fujian Medical University, Fuzhou 350009, Fujian Province, The People’s Republic of China Received November 1, 2019; Accepted January 26, 2020; Epub February 1, 2020; Published February 15, 2020 Abstract: Background: Kabuki syndrome is a rare multiple congenital anomaly syndrome characterized by distinct facial features, intellectual disability, cardiovascular and musculoskeletal abnormalities, persistence of fetal finger- tip pads, and postnatal growth deficiency. Currently, the diagnosis mainly depends on clinical manifestations and genetic testing. To date, there is no report on the identification Kabuki syndrome in fetuses using chromosomal microarray analysis (CMA). Case presentation: A fetus was identified with growth retardation and cardiovascular abnormality on color Doppler ultrasonography; however, non-invasive prenatal testing (NIPT) revealed a low risk and G-banding karyotyping revealed no abnormal karyotype detected. CMA identified a 1.3 Mb deletion on the X chromosome (Xp11.3) containing KDM6A, DUSP21, MIR222, MIR221 and CXorf36 genes. The fetus was diagnosed with Kabuki syndrome 2, and labor was induced. In addition, CMA detected a 1.3 Mb deletion in the chromosome Xp11.3 in the mother, which contains 5 genes namely KDM6A, DUSP21, MIR222, MIR221 and CXorf36, while no chromosomal abnormality was identified in the father. Conclusions: We report a fetus with Kabuki syndrome 2 detected using CMA.
    [Show full text]
  • Genetic Basis of Simple and Complex Traits with Relevance to Avian Evolution
    Genetic basis of simple and complex traits with relevance to avian evolution Małgorzata Anna Gazda Doctoral Program in Biodiversity, Genetics and Evolution D Faculdade de Ciências da Universidade do Porto 2019 Supervisor Miguel Jorge Pinto Carneiro, Auxiliary Researcher, CIBIO/InBIO, Laboratório Associado, Universidade do Porto Co-supervisor Ricardo Lopes, CIBIO/InBIO Leif Andersson, Uppsala University FCUP Genetic basis of avian traits Nota Previa Na elaboração desta tese, e nos termos do número 2 do Artigo 4º do Regulamento Geral dos Terceiros Ciclos de Estudos da Universidade do Porto e do Artigo 31º do D.L.74/2006, de 24 de Março, com a nova redação introduzida pelo D.L. 230/2009, de 14 de Setembro, foi efetuado o aproveitamento total de um conjunto coerente de trabalhos de investigação já publicados ou submetidos para publicação em revistas internacionais indexadas e com arbitragem científica, os quais integram alguns dos capítulos da presente tese. Tendo em conta que os referidos trabalhos foram realizados com a colaboração de outros autores, o candidato esclarece que, em todos eles, participou ativamente na sua conceção, na obtenção, análise e discussão de resultados, bem como na elaboração da sua forma publicada. Este trabalho foi apoiado pela Fundação para a Ciência e Tecnologia (FCT) através da atribuição de uma bolsa de doutoramento (PD/BD/114042/2015) no âmbito do programa doutoral em Biodiversidade, Genética e Evolução (BIODIV). 2 FCUP Genetic basis of avian traits Acknowledgements Firstly, I would like to thank to my all supervisors Miguel Carneiro, Ricardo Lopes and Leif Andersson, for the demanding task of supervising myself last four years.
    [Show full text]
  • A Computational Approach for Defining a Signature of Β-Cell Golgi Stress in Diabetes Mellitus
    Page 1 of 781 Diabetes A Computational Approach for Defining a Signature of β-Cell Golgi Stress in Diabetes Mellitus Robert N. Bone1,6,7, Olufunmilola Oyebamiji2, Sayali Talware2, Sharmila Selvaraj2, Preethi Krishnan3,6, Farooq Syed1,6,7, Huanmei Wu2, Carmella Evans-Molina 1,3,4,5,6,7,8* Departments of 1Pediatrics, 3Medicine, 4Anatomy, Cell Biology & Physiology, 5Biochemistry & Molecular Biology, the 6Center for Diabetes & Metabolic Diseases, and the 7Herman B. Wells Center for Pediatric Research, Indiana University School of Medicine, Indianapolis, IN 46202; 2Department of BioHealth Informatics, Indiana University-Purdue University Indianapolis, Indianapolis, IN, 46202; 8Roudebush VA Medical Center, Indianapolis, IN 46202. *Corresponding Author(s): Carmella Evans-Molina, MD, PhD ([email protected]) Indiana University School of Medicine, 635 Barnhill Drive, MS 2031A, Indianapolis, IN 46202, Telephone: (317) 274-4145, Fax (317) 274-4107 Running Title: Golgi Stress Response in Diabetes Word Count: 4358 Number of Figures: 6 Keywords: Golgi apparatus stress, Islets, β cell, Type 1 diabetes, Type 2 diabetes 1 Diabetes Publish Ahead of Print, published online August 20, 2020 Diabetes Page 2 of 781 ABSTRACT The Golgi apparatus (GA) is an important site of insulin processing and granule maturation, but whether GA organelle dysfunction and GA stress are present in the diabetic β-cell has not been tested. We utilized an informatics-based approach to develop a transcriptional signature of β-cell GA stress using existing RNA sequencing and microarray datasets generated using human islets from donors with diabetes and islets where type 1(T1D) and type 2 diabetes (T2D) had been modeled ex vivo. To narrow our results to GA-specific genes, we applied a filter set of 1,030 genes accepted as GA associated.
    [Show full text]
  • Supplementary Table
    Supporting information Additional Supporting Information may be found in the online version of this article: Supplementary Table S1: List of deregulated genes in serum of cancer patients in comparision to serum of healthy individuals (p < 0.05, logFC ≥ 1). ENTREZ Gene ID Symbol Gene Name logFC p-value q-value 8407 TAGLN2 transgelin 2 3,78 3,40E-07 0,0022 7035 TFPI tissue factor pathway inhibitor (lipoprotein-associated coagulation inhibitor) 3,53 4,30E-05 0,022 28996 HIPK2 homeodomain interacting protein kinase 2 3,49 2,50E-06 0,0066 3690 ITGB3 integrin, beta 3 (platelet glycoprotein IIIa, antigen CD61) 3,48 0,00053 0,081 7035 TFPI tissue factor pathway inhibitor (lipoprotein-associated coagulation inhibitor) 3,45 1,80E-05 0,014 4900 NRGN neurogranin (protein kinase C substrate, RC3) 3,32 0,00012 0,037 10398 MYL9 myosin, light chain 9, regulatory 3,22 8,20E-06 0,011 3796 KIF2A kinesin heavy chain member 2A 3,14 0,00015 0,04 5476 CTSA cathepsin A 3,08 0,00015 0,04 6648 SOD2 superoxide dismutase 2, mitochondrial 3,07 4,20E-06 0,0077 2982 GUCY1A3 guanylate cyclase 1, soluble, alpha 3 3,07 0,0015 0,13 8459 TPST2 tyrosylprotein sulfotransferase 2 3,05 0,00043 0,074 2983 GUCY1B3 guanylate cyclase 1, soluble, beta 3 3,04 3,70E-05 0,021 145781 GCOM1 GRINL1A complex locus 3,02 0,00027 0,059 10611 PDLIM5 PDZ and LIM domain 5 2,87 1,80E-05 0,014 5567 PRKACB protein kinase, cAMP-dependent, catalytic, beta 2,85 0,0015 0,13 25907 TMEM158 transmembrane protein 158 (gene/pseudogene) 2,84 0,0068 0,27 8848 TSC22D1 TSC22 domain family, member 1 2,83 0,00058 0,084 26 351 APP amyloid beta (A4) precursor protein 2,82 0,00018 0,045 9240 PNMA1 paraneoplastic antigen MA1 2,78 0,00028 0,06 400073 C12orf76 chromosome 12 open reading frame 76 2,78 0,00069 0,091 649260 ILMN_35781 PREDICTED: Homo sapiens similar to LIM and senescent cell antigen-like domains 1 (LOC649260), mRNA.
    [Show full text]
  • Supplementary Table S4. FGA Co-Expressed Gene List in LUAD
    Supplementary Table S4. FGA co-expressed gene list in LUAD tumors Symbol R Locus Description FGG 0.919 4q28 fibrinogen gamma chain FGL1 0.635 8p22 fibrinogen-like 1 SLC7A2 0.536 8p22 solute carrier family 7 (cationic amino acid transporter, y+ system), member 2 DUSP4 0.521 8p12-p11 dual specificity phosphatase 4 HAL 0.51 12q22-q24.1histidine ammonia-lyase PDE4D 0.499 5q12 phosphodiesterase 4D, cAMP-specific FURIN 0.497 15q26.1 furin (paired basic amino acid cleaving enzyme) CPS1 0.49 2q35 carbamoyl-phosphate synthase 1, mitochondrial TESC 0.478 12q24.22 tescalcin INHA 0.465 2q35 inhibin, alpha S100P 0.461 4p16 S100 calcium binding protein P VPS37A 0.447 8p22 vacuolar protein sorting 37 homolog A (S. cerevisiae) SLC16A14 0.447 2q36.3 solute carrier family 16, member 14 PPARGC1A 0.443 4p15.1 peroxisome proliferator-activated receptor gamma, coactivator 1 alpha SIK1 0.435 21q22.3 salt-inducible kinase 1 IRS2 0.434 13q34 insulin receptor substrate 2 RND1 0.433 12q12 Rho family GTPase 1 HGD 0.433 3q13.33 homogentisate 1,2-dioxygenase PTP4A1 0.432 6q12 protein tyrosine phosphatase type IVA, member 1 C8orf4 0.428 8p11.2 chromosome 8 open reading frame 4 DDC 0.427 7p12.2 dopa decarboxylase (aromatic L-amino acid decarboxylase) TACC2 0.427 10q26 transforming, acidic coiled-coil containing protein 2 MUC13 0.422 3q21.2 mucin 13, cell surface associated C5 0.412 9q33-q34 complement component 5 NR4A2 0.412 2q22-q23 nuclear receptor subfamily 4, group A, member 2 EYS 0.411 6q12 eyes shut homolog (Drosophila) GPX2 0.406 14q24.1 glutathione peroxidase
    [Show full text]
  • Genetic Diagnosis and Respiratory Management Of
    UITNODIGING GENETIC DIAGNOSIS Voor het bijwonen van de openbare verdediging van AND RESPIRATORY het proefschrift Genetic diagnosis and respiratory management of primary ciliary dyskinesia dyskinesia ciliary of primary management respiratory and diagnosis Genetic GENETIC DIAGNOSIS MANAGEMENT OF AND RESPIRATORY MANAGEMENT OF PRIMARY CILIARY PRIMARY CILIARY DYSKINESIA DYSKINESIA Door Tamara Paff Tamara Paff dinsdag 7 november 2017 11:45 uur in de aula van de Vrije Universiteit de Boelelaan, 1105 TE Amsterdam Receptie aansluitend in Grand cafe The Basket op de VU campus Tamara Paff Johann Keplerstraat 8-1 hoog 1098 HL, Amsterdam +31645364292/ [email protected] Tamara Paff Tamara | Paranimfen Marian van der Meij [email protected] 06-15500488 Marc van der Schee [email protected] 06-40883602 14759 - Paff_R11,5_OMS_DEF.indd 1 25-09-17 10:25 UITNODIGING GENETIC DIAGNOSIS Voor het bijwonen van de openbare verdediging van AND RESPIRATORY het proefschrift Genetic diagnosis and respiratory management of primary ciliary dyskinesia dyskinesia ciliary of primary management respiratory and diagnosis Genetic GENETIC DIAGNOSIS MANAGEMENT OF AND RESPIRATORY MANAGEMENT OF PRIMARY CILIARY PRIMARY CILIARY DYSKINESIA DYSKINESIA Door Tamara Paff Tamara Paff Dag datum tijdstip in de aula van de Vrije Universiteit de Boelelaan, 1105 TE Amsterdam Receptie aansluitend in Grand cafe The Basket op de VU campus Tamara Paff Johann Keplerstraat 8-1 hoog 1098 HL, Amsterdam +31645364292/ [email protected] Tamara Paff Tamara Paranimfen Marian van der Meij | [email protected] 06-15500488 Marc van der Schee [email protected] 06-40883602 14759_TPaff_BW.indd 1 19-09-17 13:08 ProefschriftTamaraPaff_Cover+Bladwijzer.indd All Pages 15-08-17 12:47 The studies performed in this thesis were financially supported by the PCD support group (PCD belangengroep), Fonds NutsOhra, the “Dutch mudder” team and Chiesi.
    [Show full text]
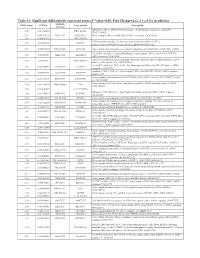
  • (P -Value<0.05, Fold Change≥1.4), 4 Vs. 0 Gy Irradiation
    Table S1: Significant differentially expressed genes (P -Value<0.05, Fold Change≥1.4), 4 vs. 0 Gy irradiation Genbank Fold Change P -Value Gene Symbol Description Accession Q9F8M7_CARHY (Q9F8M7) DTDP-glucose 4,6-dehydratase (Fragment), partial (9%) 6.70 0.017399678 THC2699065 [THC2719287] 5.53 0.003379195 BC013657 BC013657 Homo sapiens cDNA clone IMAGE:4152983, partial cds. [BC013657] 5.10 0.024641735 THC2750781 Ciliary dynein heavy chain 5 (Axonemal beta dynein heavy chain 5) (HL1). 4.07 0.04353262 DNAH5 [Source:Uniprot/SWISSPROT;Acc:Q8TE73] [ENST00000382416] 3.81 0.002855909 NM_145263 SPATA18 Homo sapiens spermatogenesis associated 18 homolog (rat) (SPATA18), mRNA [NM_145263] AA418814 zw01a02.s1 Soares_NhHMPu_S1 Homo sapiens cDNA clone IMAGE:767978 3', 3.69 0.03203913 AA418814 AA418814 mRNA sequence [AA418814] AL356953 leucine-rich repeat-containing G protein-coupled receptor 6 {Homo sapiens} (exp=0; 3.63 0.0277936 THC2705989 wgp=1; cg=0), partial (4%) [THC2752981] AA484677 ne64a07.s1 NCI_CGAP_Alv1 Homo sapiens cDNA clone IMAGE:909012, mRNA 3.63 0.027098073 AA484677 AA484677 sequence [AA484677] oe06h09.s1 NCI_CGAP_Ov2 Homo sapiens cDNA clone IMAGE:1385153, mRNA sequence 3.48 0.04468495 AA837799 AA837799 [AA837799] Homo sapiens hypothetical protein LOC340109, mRNA (cDNA clone IMAGE:5578073), partial 3.27 0.031178378 BC039509 LOC643401 cds. [BC039509] Homo sapiens Fas (TNF receptor superfamily, member 6) (FAS), transcript variant 1, mRNA 3.24 0.022156298 NM_000043 FAS [NM_000043] 3.20 0.021043295 A_32_P125056 BF803942 CM2-CI0135-021100-477-g08 CI0135 Homo sapiens cDNA, mRNA sequence 3.04 0.043389246 BF803942 BF803942 [BF803942] 3.03 0.002430239 NM_015920 RPS27L Homo sapiens ribosomal protein S27-like (RPS27L), mRNA [NM_015920] Homo sapiens tumor necrosis factor receptor superfamily, member 10c, decoy without an 2.98 0.021202829 NM_003841 TNFRSF10C intracellular domain (TNFRSF10C), mRNA [NM_003841] 2.97 0.03243901 AB002384 C6orf32 Homo sapiens mRNA for KIAA0386 gene, partial cds.
    [Show full text]
  • TCTE1 Is a Conserved Component of the Dynein Regulatory Complex and Is Required for Motility and Metabolism in Mouse Spermatozoa
    TCTE1 is a conserved component of the dynein PNAS PLUS regulatory complex and is required for motility and metabolism in mouse spermatozoa Julio M. Castanedaa,b,1, Rong Huac,d,1, Haruhiko Miyatab, Asami Ojib,e, Yueshuai Guoc,d, Yiwei Chengc,d, Tao Zhouc,d, Xuejiang Guoc,d, Yiqiang Cuic,d, Bin Shenc, Zibin Wangc, Zhibin Huc,f, Zuomin Zhouc,d, Jiahao Shac,d, Renata Prunskaite-Hyyrylainena,g,h, Zhifeng Yua,i, Ramiro Ramirez-Solisj, Masahito Ikawab,e,k,2, Martin M. Matzuka,g,i,l,m,n,2, and Mingxi Liuc,d,2 aDepartment of Pathology and Immunology, Baylor College of Medicine, Houston, TX 77030; bResearch Institute for Microbial Diseases, Osaka University, Suita, Osaka 5650871, Japan; cState Key Laboratory of Reproductive Medicine, Nanjing Medical University, Nanjing 210029, People’s Republic of China; dDepartment of Histology and Embryology, Nanjing Medical University, Nanjing 210029, People’s Republic of China; eGraduate School of Pharmaceutical Sciences, Osaka University, Suita, Osaka 5650871, Japan; fAnimal Core Facility of Nanjing Medical University, Nanjing 210029, People’s Republic of China; gCenter for Reproductive Medicine, Baylor College of Medicine, Houston, TX 77030; hFaculty of Biochemistry and Molecular Medicine, University of Oulu, Oulu FI-90014, Finland; iCenter for Drug Discovery, Baylor College of Medicine, Houston, TX 77030; jWellcome Trust Sanger Institute, Hinxton CB10 1SA, United Kingdom; kThe Institute of Medical Science, The University of Tokyo, Minato-ku, Tokyo 1088639, Japan; lDepartment of Molecular and Cellular Biology, Baylor College of Medicine, Houston, TX 77030; mDepartment of Molecular and Human Genetics, Baylor College of Medicine, Houston, TX 77030; and nDepartment of Pharmacology, Baylor College of Medicine, Houston, TX 77030 Contributed by Martin M.
    [Show full text]
  • Mapping the Landscape of Tandem Repeat Variability by Targeted Long Read Single Molecule Sequencing in Familial X-Linked Intelle
    Zablotskaya et al. BMC Medical Genomics (2018) 11:123 https://doi.org/10.1186/s12920-018-0446-7 RESEARCHARTICLE Open Access Mapping the landscape of tandem repeat variability by targeted long read single molecule sequencing in familial X-linked intellectual disability Alena Zablotskaya1, Hilde Van Esch2, Kevin J. Verstrepen3, Guy Froyen4 and Joris R. Vermeesch1* Abstract Background: The etiology of more than half of all patients with X-linked intellectual disability remains elusive, despite array-based comparative genomic hybridization, whole exome or genome sequencing. Since short read massive parallel sequencing approaches do not allow the detection of larger tandem repeat expansions, we hypothesized that such expansions could be a hidden cause of X-linked intellectual disability. Methods: We selectively captured over 1800 tandem repeats on the X chromosome and characterized them by long read single molecule sequencing in 3 families with idiopathic X-linked intellectual disability. Results: In male DNA samples, full tandem repeat length sequences were obtained for 88–93% of the targets and up to 99.6% of the repeats with a moderate guanine-cytosine content. Read length and analysis pipeline allow to detect cases of > 900 bp tandem repeat expansion. In one family, one repeat expansion co-occurs with down- regulation of the neighboring MIR222 gene. This gene has previously been implicated in intellectual disability and is apparently linked to FMR1 and NEFH overexpression associated with neurological disorders. Conclusions: This study demonstrates the power of single molecule sequencing to measure tandem repeat lengths and detect expansions, and suggests that tandem repeat mutations may be a hidden cause of X-linked intellectual disability.
    [Show full text]
  • MALE Protein Name Accession Number Molecular Weight CP1 CP2 H1 H2 PDAC1 PDAC2 CP Mean H Mean PDAC Mean T-Test PDAC Vs. H T-Test
    MALE t-test t-test Accession Molecular H PDAC PDAC vs. PDAC vs. Protein Name Number Weight CP1 CP2 H1 H2 PDAC1 PDAC2 CP Mean Mean Mean H CP PDAC/H PDAC/CP - 22 kDa protein IPI00219910 22 kDa 7 5 4 8 1 0 6 6 1 0.1126 0.0456 0.1 0.1 - Cold agglutinin FS-1 L-chain (Fragment) IPI00827773 12 kDa 32 39 34 26 53 57 36 30 55 0.0309 0.0388 1.8 1.5 - HRV Fab 027-VL (Fragment) IPI00827643 12 kDa 4 6 0 0 0 0 5 0 0 - 0.0574 - 0.0 - REV25-2 (Fragment) IPI00816794 15 kDa 8 12 5 7 8 9 10 6 8 0.2225 0.3844 1.3 0.8 A1BG Alpha-1B-glycoprotein precursor IPI00022895 54 kDa 115 109 106 112 111 100 112 109 105 0.6497 0.4138 1.0 0.9 A2M Alpha-2-macroglobulin precursor IPI00478003 163 kDa 62 63 86 72 14 18 63 79 16 0.0120 0.0019 0.2 0.3 ABCB1 Multidrug resistance protein 1 IPI00027481 141 kDa 41 46 23 26 52 64 43 25 58 0.0355 0.1660 2.4 1.3 ABHD14B Isoform 1 of Abhydrolase domain-containing proteinIPI00063827 14B 22 kDa 19 15 19 17 15 9 17 18 12 0.2502 0.3306 0.7 0.7 ABP1 Isoform 1 of Amiloride-sensitive amine oxidase [copper-containing]IPI00020982 precursor85 kDa 1 5 8 8 0 0 3 8 0 0.0001 0.2445 0.0 0.0 ACAN aggrecan isoform 2 precursor IPI00027377 250 kDa 38 30 17 28 34 24 34 22 29 0.4877 0.5109 1.3 0.8 ACE Isoform Somatic-1 of Angiotensin-converting enzyme, somaticIPI00437751 isoform precursor150 kDa 48 34 67 56 28 38 41 61 33 0.0600 0.4301 0.5 0.8 ACE2 Isoform 1 of Angiotensin-converting enzyme 2 precursorIPI00465187 92 kDa 11 16 20 30 4 5 13 25 5 0.0557 0.0847 0.2 0.4 ACO1 Cytoplasmic aconitate hydratase IPI00008485 98 kDa 2 2 0 0 0 0 2 0 0 - 0.0081 - 0.0
    [Show full text]
  • Whole Genome Sequencing of Familial Non-Medullary Thyroid Cancer Identifies Germline Alterations in MAPK/ERK and PI3K/AKT Signaling Pathways
    biomolecules Article Whole Genome Sequencing of Familial Non-Medullary Thyroid Cancer Identifies Germline Alterations in MAPK/ERK and PI3K/AKT Signaling Pathways Aayushi Srivastava 1,2,3,4 , Abhishek Kumar 1,5,6 , Sara Giangiobbe 1, Elena Bonora 7, Kari Hemminki 1, Asta Försti 1,2,3 and Obul Reddy Bandapalli 1,2,3,* 1 Division of Molecular Genetic Epidemiology, German Cancer Research Center (DKFZ), D-69120 Heidelberg, Germany; [email protected] (A.S.); [email protected] (A.K.); [email protected] (S.G.); [email protected] (K.H.); [email protected] (A.F.) 2 Hopp Children’s Cancer Center (KiTZ), D-69120 Heidelberg, Germany 3 Division of Pediatric Neurooncology, German Cancer Research Center (DKFZ), German Cancer Consortium (DKTK), D-69120 Heidelberg, Germany 4 Medical Faculty, Heidelberg University, D-69120 Heidelberg, Germany 5 Institute of Bioinformatics, International Technology Park, Bangalore 560066, India 6 Manipal Academy of Higher Education (MAHE), Manipal, Karnataka 576104, India 7 S.Orsola-Malphigi Hospital, Unit of Medical Genetics, 40138 Bologna, Italy; [email protected] * Correspondence: [email protected]; Tel.: +49-6221-42-1709 Received: 29 August 2019; Accepted: 10 October 2019; Published: 13 October 2019 Abstract: Evidence of familial inheritance in non-medullary thyroid cancer (NMTC) has accumulated over the last few decades. However, known variants account for a very small percentage of the genetic burden. Here, we focused on the identification of common pathways and networks enriched in NMTC families to better understand its pathogenesis with the final aim of identifying one novel high/moderate-penetrance germline predisposition variant segregating with the disease in each studied family.
    [Show full text]
  • Human Induced Pluripotent Stem Cell–Derived Podocytes Mature Into Vascularized Glomeruli Upon Experimental Transplantation
    BASIC RESEARCH www.jasn.org Human Induced Pluripotent Stem Cell–Derived Podocytes Mature into Vascularized Glomeruli upon Experimental Transplantation † Sazia Sharmin,* Atsuhiro Taguchi,* Yusuke Kaku,* Yasuhiro Yoshimura,* Tomoko Ohmori,* ‡ † ‡ Tetsushi Sakuma, Masashi Mukoyama, Takashi Yamamoto, Hidetake Kurihara,§ and | Ryuichi Nishinakamura* *Department of Kidney Development, Institute of Molecular Embryology and Genetics, and †Department of Nephrology, Faculty of Life Sciences, Kumamoto University, Kumamoto, Japan; ‡Department of Mathematical and Life Sciences, Graduate School of Science, Hiroshima University, Hiroshima, Japan; §Division of Anatomy, Juntendo University School of Medicine, Tokyo, Japan; and |Japan Science and Technology Agency, CREST, Kumamoto, Japan ABSTRACT Glomerular podocytes express proteins, such as nephrin, that constitute the slit diaphragm, thereby contributing to the filtration process in the kidney. Glomerular development has been analyzed mainly in mice, whereas analysis of human kidney development has been minimal because of limited access to embryonic kidneys. We previously reported the induction of three-dimensional primordial glomeruli from human induced pluripotent stem (iPS) cells. Here, using transcription activator–like effector nuclease-mediated homologous recombination, we generated human iPS cell lines that express green fluorescent protein (GFP) in the NPHS1 locus, which encodes nephrin, and we show that GFP expression facilitated accurate visualization of nephrin-positive podocyte formation in
    [Show full text]