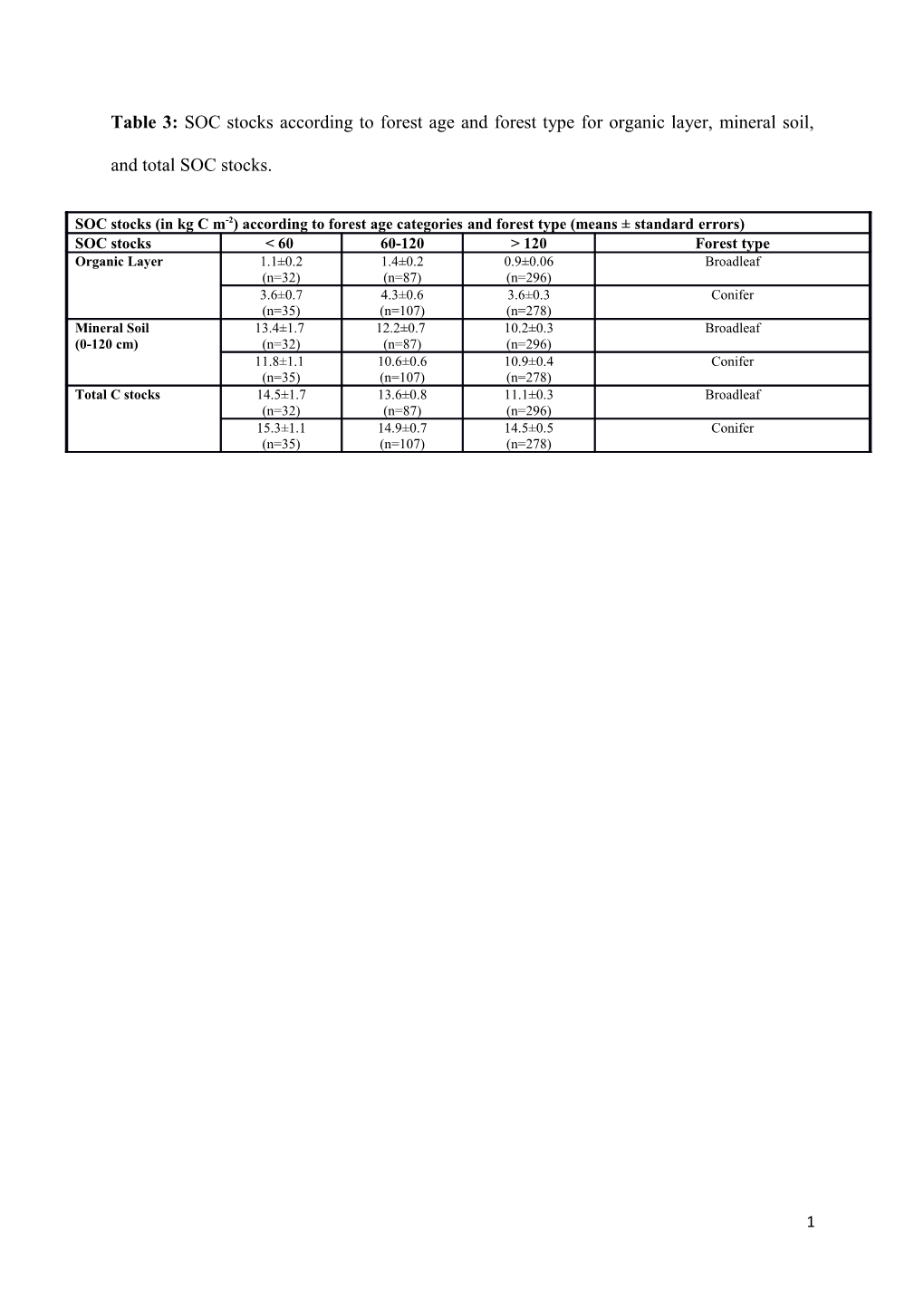
Table 4: ANOVA Models Indicating Order of Variables Used for the Analysis

Table 3: SOC stocks according to forest age and forest type for organic layer, mineral soil,

and total SOC stocks.

SOC stocks (in kg C m-2) according to forest age categories and forest type (means ± standard errors) SOC stocks < 60 60-120 > 120 Forest type Organic Layer 1.1±0.2 1.4±0.2 0.9±0.06 Broadleaf (n=32) (n=87) (n=296) 3.6±0.7 4.3±0.6 3.6±0.3 Conifer (n=35) (n=107) (n=278) Mineral Soil 13.4±1.7 12.2±0.7 10.2±0.3 Broadleaf (0-120 cm) (n=32) (n=87) (n=296) 11.8±1.1 10.6±0.6 10.9±0.4 Conifer (n=35) (n=107) (n=278) Total C stocks 14.5±1.7 13.6±0.8 11.1±0.3 Broadleaf (n=32) (n=87) (n=296) 15.3±1.1 14.9±0.7 14.5±0.5 Conifer (n=35) (n=107) (n=278)

1 Table 4: ANOVA models indicating order of variables used for the analysis.

ANOVA (with function aov.ko) Organic layer summary(model <- aov.ko(log-transformed(organic layer) ~ Region*Soil group + BC*Soil group + Forest age*Soil group + MAT + pH*Forest type, data=Forest age) Mineral soil summary(model <- aov.ko(log-transformed(mineral soil) ~ Region*Soil group + Forest age*Soil group + MAP + Slope + Altitude + Sand content + BC*Soil group + Soil type*BC + Forest type, data=Forest age) Total C stocks summary(model <- aov.ko(log-transformed(total C stocks) ~ Region*Soil group + Forest age*Soil group + BC + BC*Soil group + Relief + Forest type + Slope + MAP + MAT, data= Forest age) The sign “*” denotes an interaction between two covariates. Fitted models are not shown.

Table 5: Results from Post hoc TukeyHSD tests comparing the means of the three forest age

categories.

TukeyHSD post-hoc tests Tukey multiple comparisons of means 95% family-wise confidence interval Forest age Diff Lwr Upr P adj comparison Organic layer Medium - Young 0.23 -0.22 0.68 0.5 Old - Young -0.06 -0.47 0.35 0.9 Old - Medium -0.29 -0.56 -0.03 0.03 Mineral soil Medium - Young -0.03 -0.21 0.16 0.9 Old - Young -0.11 -0.27 0.06 0.26 Old - Medium -0.08 -0.18 0.03 0.17 Total Medium - Young -0.02 -0.19 0.15 0.9 C stocks Old - Young -0.15 -0.30 0.00 0.05 Old - Medium -0.13 -0.23 -0.03 0.006 Confidence level is 0.95, data presents lower and upper limits, their average and the adjusted p-values.

Table 6: ANOVA results on the effect of forest age and other variables on SOC stocks for the five biogeographic regions of Switzerland.

Region Organic Layer Mineral Soil Covariate Df SS (%) F Covariate Df SS (%) F Jura Soil group 2 19.2 F(2,65) = 9.952 Soil group 2 14.6 F(2,66) = *** 7.847 ***

pH 1 3.1 F(1,65) = 3.191 BC 1 12.3 F(1,66) = . 13.218 ***

Soil group x 3 14.9 F(3,65) = 5.164 Forest type 1 5.1 F(1,66) = BC ** 5.493 *

- - - - Slope 1 6.3 F(1,66) =

2 6.775 * Residuals 65 62.8 - Residuals 66 61.7 - Swiss Soil group 2 14.4 F(2,264) = Soil group 2 8.2 F(2,263) = Plateau 33.476 *** 16.311 *** BC 1 9.5 F(1,264) = BC 1 5.5 F(1,263) = 44.422 *** 21.924 ***

MAT 1 1.0 F(1,264) = Slope 1 8.8 F(1,263) = 4.536 * 35.189 ***

pH 1 7.3 F(1,264) = MAP 1 5.6 F(1,263) = 33.867 *** 22.325 ***

Forest type 1 3.5 F(1,264) = Soil group x 2 2.7 F(2,263) = 16.415 *** BC 5.412 **

Soil group x 2 5.9 F(2,264) = Soil group x 6 3.3 F(6,263) = BC 13.784 *** Forest age 2.171 *

pH x Forest 1 1.7 F(1,264) = - - - - type 7.842 ** Residuals 264 56.7 - Residuals 263 65.9 - Pre-Alps Soil group 2 13.3 F(2, 248) = Soil group 2 5.0 F(2,251) = 38.980 *** 8.551 ***

BC 1 18.3 F(1,248) = BC 1 4.7 F(1,251) = 106.945 *** 16.126 ***

MAT 1 4.2 F(1, 248) = Forest type 1 6.9 F(1,251) = 24.537 *** 23.534 ***

pH 1 9.0 F(1, 248) = Slope 1 3.0 F(1,251) = 52.696 *** 9.904 **

Forest type 1 1.7 F(1, 248) = MAP 1 6.8 F(1,251) = 9.826 ** 23.293 ***

Soil group x 2 7.7 F(2, 248) = - - - - BC 22.472 ***

pH x Forest 1 3.3 F(1, 248) = - - - - type 19.088 *** Residuals 248 42.5 - Residuals 251 73.6 - Alps Soil group 2 8.4 F(2, 156) = Soil group 2 5.9 F(2,155) = 9.176 *** 7.190 **

BC 1 10.9 F(1, 156) = BC 1 13.7 F(1,155) = 23.876 *** 32.795 ***

MAT 1 2.3 F(1, 156) = Forest age 2 2.5 F(1,155) = 4.902 * 3.032 .

pH 1 3.4 F(1, 156) = Slope 1 2.7 F(1,155) = 7.431 ** 6.397 **

Forest type 1 3.7 F(1, 156) = MAP 1 10.6 F(1,155) = 8.190 ** 25.347 *** Residuals 156 71.3 - Residuals 155 64.6 - Souther MAT 1 23.0 F(1,65) = Soil group 2 6.4 F(2,65) = n Alps 26.568 *** 2.756 . pH 1 8.0 F(1,65) = 9.227 MAP 1 3.4 F(1,65) = ** 2.935 .

Soil group x 3 12.7 F(3,65) = 4.880 Soil group x 2 14.7 F(1,65) = BC ** BC 6.330 ** Residuals 65 56.3 - Residuals 65 75.5 - The abbreviation df stands for degrees of freedom, SS represents the sum of squares in %, F represents the F-value. The annotation (“-”) means that the variable was not present in the final model fit.

3 Figure 8: TukeyHSD plots comparing the means of the three different forest categories for C stocks in organic layer, mineral soil (0-120 cm soil depth), and total C stocks (top to bottom).

Lines represent the differences in means between forest age groups (from top to bottom: medium vs. young, old vs. young, and old vs. medium, respectively). If a line crosses the 0.0 dashed mark, there is no significant difference between the means of the examined groups, if it does not – there is a significant difference.

4 Figure 9: Distribution of SOC stocks (kg C m-2) according to the five bio-geographic regions of Switzerland (top dashed: organic layer, bottom grey: mineral soil at 0-120 cm soil depth), subdivided by forest age categories. Whiskers indicate standard errors, numbers above forest age categories – number of sites per forest age category. The category ‘young forests’ was not present in the region of Jura.

5 Figure 10: Distribution of SOC stocks (kg C m-2) according to a more detailed separation of forest age (top dashed: organic layer, bottom grey: mineral soil at 0-120 cm soil depth).

Whiskers indicate standard errors, numbers above forest age categories – number of sites per forest age category.