Pdf Nord Modular
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Minimoog Model D Manual
3 IMPORTANT SAFETY INSTRUCTIONS WARNING - WHEN USING ELECTRIC PRODUCTS, THESE BASIC PRECAUTIONS SHOULD ALWAYS BE FOLLOWED. 1. Read all the instructions before using the product. 2. Do not use this product near water - for example, near a bathtub, washbowl, kitchen sink, in a wet basement, or near a swimming pool or the like. 3. This product, in combination with an amplifier and headphones or speakers, may be capable of producing sound levels that could cause permanent hearing loss. Do not operate for a long period of time at a high volume level or at a level that is uncomfortable. 4. The product should be located so that its location does not interfere with its proper ventilation. 5. The product should be located away from heat sources such as radiators, heat registers, or other products that produce heat. No naked flame sources (such as candles, lighters, etc.) should be placed near this product. Do not operate in direct sunlight. 6. The product should be connected to a power supply only of the type described in the operating instructions or as marked on the product. 7. The power supply cord of the product should be unplugged from the outlet when left unused for a long period of time or during lightning storms. 8. Care should be taken so that objects do not fall and liquids are not spilled into the enclosure through openings. There are no user serviceable parts inside. Refer all servicing to qualified personnel only. NOTE: This equipment has been tested and found to comply with the limits for a class B digital device, pursuant to part 15 of the FCC rules. -

Modular Synthesizers
Modular Synthesizers A Brief History and Functional Description of the Modular Music Synthesizer • James Husted Synthwerks, LLC Sunday, March 24, 13 Mod•u•lar - adjective French modulaire or directly from Modern Latin modularis, from Latin modulus "a small measure" 1 : of, relating to, or based on a module or a modulus 2 : constructed with standardized units or dimensions for flexibility and variety in use, as in modular furniture 3 : composed of interchangeable units (!rst recorded 1936) Sunday, March 24, 13 Syn•the•sis - noun Etymology: Greek, from syntithenai to put together 1 : the composition or combination of parts or elements so as to form a whole 2 : the combining of often diverse conceptions into a coherent whole; also : the complex so formed Sunday, March 24, 13 Who’s on first? • 1837 - C.G. Page (Salem. Mass) - !rst to produce electronically generated sound (not necessarily associated with a musical instrument). • 1885 - Person and Ernst Lorenz -'Elektrisches Musikinstrument' - the !rst musical instrument designed to produce electrically generated sound. • 1897 - Taddaeus Cahills - Telharmonium - electromechanical instrument. • 1936 - Oskar Sala - Mixturtrautonium - !rst synth using Subharmonic synthesis • 1939 - Homer Dudley invents the Parallel Bandpass Vocoder (VODER) - A key operated speech synthesizer • 1940 - Homer Dudley invents the The Voder speech synthesizer as a way to transmit speech over telephone lines • 1948 - Hugh LeCaine - Electronic Sackbut - First voltage-controlled synthesizer • 1948 - Dr. Raymond Scott - Wall of Sound - First polyphonic Sequencing Workstation (electromechanical) and the Electronum - !rst sequencer. • 1950 - CSIR - Mk 1 - The !rst known use of a digital computer for the purpose playing music • 1956 - Louie and Bebe Barron - Produced the !rst all-electronic musical score for a major motion picture - MGM's 'Forbidden Planet' • 1957 - Max V. -

A Framework for Embedded Digital Musical Instruments
A Framework for Embedded Digital Musical Instruments Ivan Franco Music Technology Area Schulich School of Music McGill University Montreal, Canada A thesis submitted to McGill University in partial fulfillment of the requirements for the degree of Doctor of Philosophy. © 2019 Ivan Franco 2019/04/11 i Abstract Gestural controllers allow musicians to use computers as digital musical instruments (DMI). The body gestures of the performer are captured by sensors on the controller and sent as digital control data to a audio synthesis software. Until now DMIs have been largely dependent on the computing power of desktop and laptop computers but the most recent generations of single-board computers have enough processing power to satisfy the requirements of many DMIs. The advantage of those single-board computers over traditional computers is that they are much smaller in size. They can be easily embedded inside the body of the controller and used to create fully integrated and self-contained DMIs. This dissertation examines various applications of embedded computing technologies in DMIs. First we describe the history of DMIs and then expose some of the limitations associated with the use of general-purpose computers. Next we present a review on different technologies applicable to embedded DMIs and a state of the art of instruments and frameworks. Finally, we propose new technical and conceptual avenues, materialized through the Prynth framework, developed by the author and a team of collaborators during the course of this research. The Prynth framework allows instrument makers to have a solid starting point for the de- velopment of their own embedded DMIs. -

PRODUCT CATALOG WINTER 2014 the Original Red Keyboards the Nord Factory Is Located in the Creative Area of Stockholm Also Known As Sofo, in the District of Södermalm
Nord Keyboards Product Catalog Winter Catalog Product Keyboards Nord SYNTHESIZERS • STAGE PIANOS • COMBO ORGAN Handmade in Sweden by Clavia DMI AB 2014 PRODUCT CATALOG WINTER 2014 The Original Red Keyboards The Nord factory is located in the creative area of Stockholm also known as SoFo, in the district of Södermalm. With everything located in the same building, communication between development and production is only a matter of walking a few meters. We are proud to say all our Nord products are assembled by hand and they all go through a series of tough tests to ensure they’ll be ready for a long and happy life ‘on the road’. CONTENTS SYNTHESIZERS NORD LEAD A1 6 NEW NORD LEAD 4 14 NORD DRUM 2 22 STAGE PIANOS NORD ELECTRO 4 26 NORD PIANO 2 34 NORD STAGE 2 40 COMBO ORGAN NORD C2D 48 SOUND LIBRARIES 56 Manufacturer: Clavia DMI AB, Box 4214, SE-102 65 Stockholm, Sweden Phone: +46 8 442 73 60 | Fax: +46 8 644 26 50 | Email: [email protected] | www.nordkeyboards.com 3 IT ALL STARTED BACK IN 1983... In 1983 founder Hans Nordelius created the Digital In 2001 the first Nord Electro was released, In 2008 we released the Nord Electro 3 and the Percussion Plate 1 – the first drum pad allowing for introducing stunning emulations of classic vintage exclusively licensed sounds from the Mellotron and dynamic playing using sampled sounds. The DPP1 electro-mechanical instruments with a level of Chamberlin. The Electro 3 became one of the most was an instant success and soon thereafter the portability generally not associated with the original successful products we’ve ever made. -

Opsix Owner's Manual
Owner’s Manual E 2 Table of Contents Introduction .......................................................................... 6 1. Main Features ...............................................................................6 2. About the sound generator of the opsix ....................................7 Operator (modulator, carrier) .................................................................................................................... 7 Algorithms ........................................................................................................................................................ 7 Operator modes ............................................................................................................................................. 7 3. Block Diagram ............................................................................11 Panel description and functions ....................................... 12 1. Front panel ..................................................................................12 2. Rear panel connections ..............................................................15 Connecting the AC adapter ......................................................................................................................15 Other connections .......................................................................................................................................15 Operation Guide ................................................................. 17 1. Turning the power on/off ...........................................................17 -

Theory and Practice of Modified Frequency Modulation Synthesis*
PAPERS Theory and Practice of Modified Frequency Modulation Synthesis* VICTOR LAZZARINI AND JOSEPH TIMONEY ([email protected]) ([email protected]) Sound and Music Technology Group, National University of Ireland, Maynooth, Ireland The theory and applications of a variant of the well-known synthesis method of frequency modulation, modified frequency modulation (ModFM), is discussed. The technique addresses some of the shortcomings of classic FM and provides a more smoothly evolving spectrum with respect to variations in the modulation index. A complete description of the method is provided, discussing its characteristics and practical considerations of instrument design. A phase synchronous version of ModFM is presented and its applications on resonant and formant synthesis are explored. Extensions to the technique are introduced, providing means of changing spectral envelope symmetry. Finally its applications as an adaptive effect are discussed. Sound examples for the various applications of the technique are offered online. 0 INTRODUCTION tion we will examine further applications in complement to the ones presented in [11]. We will also look at exten- The elegance and efficiency of closed-form formulas, sions to the basic technique as well as its use as an adap- which arise in various distortion synthesis algorithms, rep- tive effect. resent a resource for instrument design that is explored too rarely. Among the many techniques in this group there 1 SIMPLE MODFM SYNTHESIS are frequency modulation synthesis [1], summation formula method [2], nonlinear waveshaping [3], [4], and phase dis- ModFM synthesis represents an interesting alternative tortion [5]. Some of these techniques remain largely for- to the well-known FM [1] (or phase-modulation) synthe- gotten, even when many useful applications for them can sis. -

Vector Synthesis: a Media Archaeological Investigation Into Sound-Modulated Light
VECTOR SYNTHESIS: A MEDIA ARCHAEOLOGICAL INVESTIGATION INTO SOUND-MODULATED LIGHT Submitted for the qualification Master of Arts in Sound in New Media, Department of Media, Aalto University, Helsinki FI April, 2019 Supervisor: Antti Ikonen Advisor: Marco Donnarumma DEREK HOLZER [BLANK PAGE] Aalto University, P.O. BOX 11000, 00076 AALTO www.aalto.fi Master of Arts thesis abstract Author Derek Holzer Title of thesis Vector Synthesis: a Media-Archaeological Investigation into Sound-Modulated Light Department Department of Media Degree programme Sound in New Media Year 2019 Number of pages 121 Language English Abstract Vector Synthesis is a computational art project inspired by theories of media archaeology, by the history of computer and video art, and by the use of discarded and obsolete technologies such as the Cathode Ray Tube monitor. This text explores the military and techno-scientific legacies at the birth of modern computing, and charts attempts by artists of the subsequent two decades to decouple these tools from their destructive origins. Using this history as a basis, the author then describes a media archaeological, real time performance system using audio synthesis and vector graphics display techniques to investigate direct, synesthetic relationships between sound and image. Key to this system, realized in the Pure Data programming environment, is a didactic, open source approach which encourages reuse and modification by other artists within the experimental audiovisual arts community. Keywords media art, media-archaeology, audiovisual performance, open source code, cathode- ray tubes, obsolete technology, synesthesia, vector graphics, audio synthesis, video art [BLANK PAGE] O22 ABSTRACT Vector Synthesis is a computational art project inspired by theories of media archaeology, by the history of computer and video art, and by the use of discarded and obsolete technologies such as the Cathode Ray Tube monitor. -
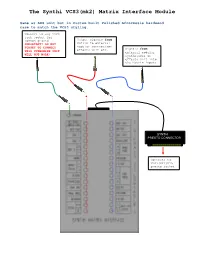
The Synthi VCS3(Mk2) Matrix Interface Module
The Synthi VCS3(mk2) Matrix Interface Module Same as AKS unit but in Custom built Polished Afrormosia hardwood case to match the VCS3 styling. Connect to any VCS3 jack socket for common ground Output signals from Matrix to external IMPORTANT! DO NOT FORGET TO CONNECT modular synthesizer effects unit etc. Signals from THIS OTHERWISE UNIT external modular WILL NOT WORK! synthesizer or effects unit into the Matrix inputs SYNTHI PRESTO CONNECTOR Connects to VCS3(mk2)via presto socket Nn Using the VCS3(mk2)Matrix Interface Module This unit is functionally identical to a similar unit I designed for interfacing to the Synthi AKS. This one however is built into a cool looking polished afrormosia hardwood case. This is exactly the same wood as used on the VCS3 (mk1 or mk2). The front panel is cnc engraved satin anodised silver that complements that of the silver panelled VCS3 mk2’s. Its a complete interface unit for the VCS3(mk2) Matrix...or in other words a 'breakout' box whereby the row/column signals of the Matrix are taken out to 3.5mm jack sockets. This allows powerful interfacing options of the VCS3 with an external modular synthesizer like eg Doepfer-Eurorack and/or external effects racks etc. Note that VCS3 mk1’s don’t have a presto connector unless it has been added as a mod. Therefore this unit is designed only for use with the VCS3(mk2) with a prestopatch connector (some mk2’s from the ‘Datanomics’ period didnt come with them fitted). The panel layout also reflects the mk2 matrix layout which was different from that on the mk1. -

Rack Mount Edition by R.Stephen Dunnington
USER’s MANUAL for the Rack Mount Edition By R.Stephen Dunnington Here it is – the Minimoog Voyager Rack Mount Edition®. Moog Music has put more than 30 years of experience with analog synthesizer technology into the design of this instrument to bring you the fattest lead synthesizer since the minimoog was introduced in 1970. We’ve done away with the things that made 30-year- old analog synthesizers difficult – the tuning instability, the lack of patch memory, and the lack of compatibility with MIDI gear. We’ve kept the good parts – the rugged construction, the fun of changing a sound with knobs in real time, and the amazing, warm, fat, pleasing analog sound. The Voyager is our invitation to you to explore analog synthesis and express yourself. It doesn’t matter what style of music you play – the Voyager is here to help you tear it up in the studio, on stage, or in the privacy of your own home. Have fun! Acknowledgements – Thanks to Bob Moog for designing yet another fantastic music making machine! Thanks are also due to the Moog Music Team, Rudi Linhard of Lintronics for his amazing software, Brian Kehew, Nigel Hopkins, and all the great folks who contributed design ideas, and of course, you – the Moog Music customer. TABLE OF CONTENTS: I. Getting Started……………………………………………………... 2 II. The Basics of Analog Synthesis…………………………………… 5 III. Basic MIDI................................................................................ 12 IV. The Voyager’s Features…………………………………………… 13 V. The Voyager’s Components A. Mixer……………………………………………………………... 17 B. Oscillators……………………………………………………….. 19 C. Filters…………………………………………………………….. 22 D. Envelope Generators………………………………………….. 26 E. Audio Outputs…………………………………………………… 28 F. -

The Synth Issue
THE SYNTH ISSUE KORG ARP ODYSSEY REDUX REVIEWED HANDS ON PREVIEWS Sequential Prophet-6 Moog System 55 Modular Modal Electronics 002 MODES DEMYSTIFIED No Sheet Music Required FAKE IT ’TIL YOU MAKE IT Bigger Samples Aren’t Always Better ROLAND JD-Xi SPACESTATION 3 ARTURIA Meet the Mid-Side Stereo iPROPHET SLOW BLUES MASTER CLASS Mini-Synth to Beat from One Amp Vector Victory Get the Real-Deal Feel 5.2015 | $5.99 A MUSIC PLAYER PUBLICATION 40 YEARS OF GROUNDBREAKING SYNTHS Grammy® winner and MIDI co-creator Dave Smith has designed more groundbreaking synths than anyone. Ever. Whatever your musical need or budget, Dave’s award-winning line of analog and analog/digital hybrid instruments has the right tool for you. Pro 2 · Prophet 12 · Prophet ’08 Mopho · Mopho x4 · Mopho SE Tetra · Tempest · Evolver THE PROPHET-6 IS COMING SOON! www.davesmithinstruments.com Designed and built in California CONTENTS MAY 2015 KNOW TALK 32 SYNTH SOLOING CÞ 8 Voices, tips, and breaking news from the Keyboard community. 4 œ œ We’ve explored his sound; now dive &4 œ œ œ Jan Hammer NEW GEAR SYNTH EDITION into the playing style of . D minor pentatonic 34 BEYOND THE MANUAL 10 In our special synthesizer-focused issue, we bring you first-look Learn tweaks to get more soft synth coverage of the Dave Smith Instruments Prophet 6, Modal mileage from your computer. Electronics 002, and Moog’s Modular systems, plus ten more new synth releases. 36 DANCE Making classic sounds with the ARP. HEAR REVIEW 16 ROAD WARRIORS In NRBQ’s 50th anniversary year, keyboardist 38 ANALOG SYNTH and founding member Terry Adams discusses Korg ARP Odyssey his touring gear, and the Monk tribute he’s always dreamed of making. -

Fusion Best of Vintage Keys 1 to 4 Content
- Sound Research & Development - Fusion Best of Vintage Keys 1-4 Sample Libraries with Program Presets Banks for Alesis Fusion 8HD/6HD. The Best of Vintage Keys series provides the essence of no less than 28 real legends which wrote music history. All sounds were programmed on the original instruments and then carefully sampled for finest sound quality. This handpicked selection offers the typical sounds these instruments are famous for. And a decent Controller Assignment system allows a true rendition of the original performance control. Packed in the 4 titles “Best of Vintage Keys 1-4”, each with the focus on 7 instruments. Available separately and as complete bundle. Sophisticated Controller programming for Control Knobs 1-4, S1 and S2 switches, Trigger Buttons T1-T4, Modulation Wheel, Pitch Bend. Best of Vintage Keys 1 Featured instruments: - Yamaha CS80 - Oberheim Matrix 12 - Mellotron - Minimoog - Korg Mono/Poly - Solina String Ensemble - Elka Synthex Best of Vintage Keys 2 Featured instruments: - Rhodes Chroma - Yamaha DX7II Centennial Version E! - Roland Jupiter 8 - Memorymoog - PPG Wave 2.2 - ARP ProSoloist - Roland VP330 Best of Vintage Keys 3 Featured Instruments: - miniKORG 700S - Godwin Symphoniy - Oberheim OB8 - ARP Odyssey - Polymoog - Polivoks - Korg Trident MkII Best of Vintage Keys 4 Featured instruments: - Korg DW8000 - Farfisa Polychrome - Roland Jupiter 4 - Moog Taurus - Moog Modular - SCI Prophet 5 - ARP Quadra Bonus instruments: - Yamaha PS20 - Casio VL1 General Controller and FX Assignment Use following Controllers -

Let's Get Started…
Welcome to the OASYS Experience! This tour guide is your first stop on an amazing journey of discovery. Our goal here is to get you comfortable working with the user interface and control surface, and to give you a “sneak peek” at some of the many incredibly-musical things that you can do with OASYS! After you’ve finished this tour, you can learn more about this great instrument by working with the OASYS Operation and Parameter Guides. And you’ll find new OASYS tutorials, tips and tricks, and support materials by visiting www.korg.com/oasys and www.karma-labs.com/oasys on a regular basis! Let’s get started… Start by loading the factory data and listening to the demo songs: The factory demos allow you to experience OASYS in all of its glory - as a full production studio! In addition to hearing MIDI tracks which show off OASYS’ superb synth engines, several of the demo songs include HD audio tracks and sample data. 1. Press the DISK button > Select the FACTORY folder on the internal hard drive, and then press Open > Select the file PRELOAD.PCG, and then press Load > Check the boxes next to PRELOAD.SNG and PRELOAD.KSC, and then press OK. This will load the factory sounds, demo songs and samples. 2. Press the SEQ button, and then press the SEQ START/STOP button to play the first demo song, “Sinfonia Russe” > Press the SEQ START/STOP button again when finished listening to this song, and then press the pop-up arrow left of the song name, select and playback the other demo songs.