Suns-VOC characteristics of high performance kesterite solar cells
Oki Gunawan, Tayfun Gokmen, David B. Mitzi IBM T. J. Watson Research Center, PO Box 218, Yorktown Heights, NY 10598 USA
SUPPLEMENTARY MATERIALS
A. Suns-VOC and Suns-ISC measurement
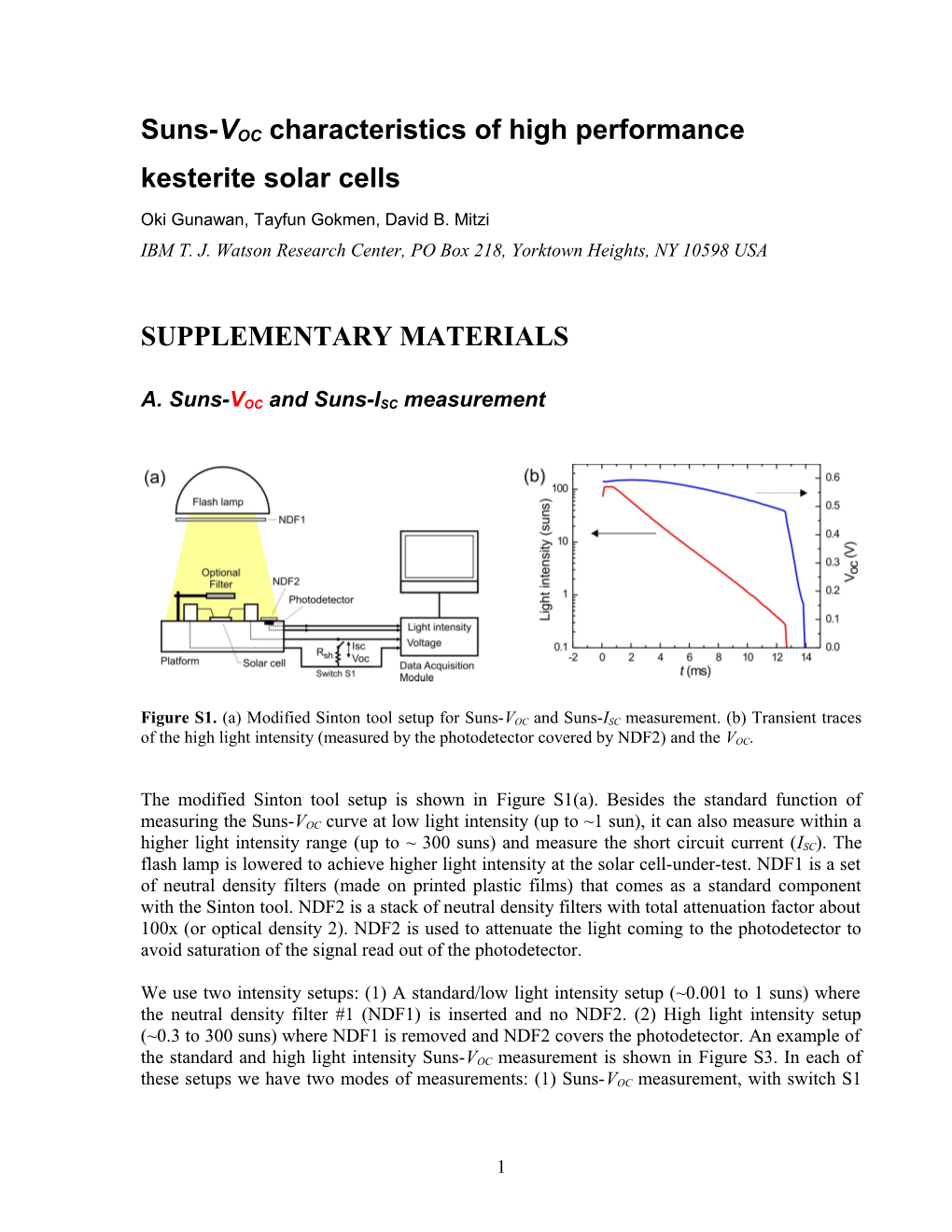
Figure S1. (a) Modified Sinton tool setup for Suns-VOC and Suns-ISC measurement. (b) Transient traces of the high light intensity (measured by the photodetector covered by NDF2) and the VOC.
The modified Sinton tool setup is shown in Figure S1(a). Besides the standard function of measuring the Suns-VOC curve at low light intensity (up to ~1 sun), it can also measure within a higher light intensity range (up to ~ 300 suns) and measure the short circuit current (ISC). The flash lamp is lowered to achieve higher light intensity at the solar cell-under-test. NDF1 is a set of neutral density filters (made on printed plastic films) that comes as a standard component with the Sinton tool. NDF2 is a stack of neutral density filters with total attenuation factor about 100x (or optical density 2). NDF2 is used to attenuate the light coming to the photodetector to avoid saturation of the signal read out of the photodetector.
We use two intensity setups: (1) A standard/low light intensity setup (~0.001 to 1 suns) where the neutral density filter #1 (NDF1) is inserted and no NDF2. (2) High light intensity setup (~0.3 to 300 suns) where NDF1 is removed and NDF2 covers the photodetector. An example of the standard and high light intensity Suns-VOC measurement is shown in Figure S3. In each of these setups we have two modes of measurements: (1) Suns-VOC measurement, with switch S1
1 open, and (2) Suns-ISC measurement, with switch S1 closed, thereby connecting the shunt resistance (Rsh) across the voltage read out.
Figure S2. Measurement example of: (a) Suns-VOC curve. Short circuit current scale is shown on the right using the ISC/S factor calculated from Suns-ISC measurement. (b) Suns-ISC measurement. Similar to
Suns-VOC measurements except the measurement is shunted with Rsh = 1 and with voltage offset correction of DVOFST = 2.07 mV .
The transient plot of the suns-VOC is shown in Figure S2. We could also plot this as ISC-VOC if we know the ISC/S factor, where S is the light intensity in suns, that can be determined from suns-ISC measurement as shown in Figure S2(b).
We can perform the Sun-ISC measurement by shunting the VOC voltage read out by a small shunt resistance e.g. RSH = 1 . The short circuit current at any intensity can be calculated as
ISC= V OC'/ R SH where VOC’ is the shunted “open circuit voltage” measured by the Sinton tool.
The raw data of this Sun-ISC curve is shown as the dotted line in Figure S2(b). However there is a small voltage offset ( DVOFST ) that usually occurs in the analog amplifier input stage of the data acquisition module. This offset voltage (~2 mV) is not negligible compared to the voltage being measured in the shunted condition (VOC’ ~ 0.1 – 100 mV). Thus the raw data of the Suns- ISC curve [dotted line, Figure S2(b)] does not look like a straight line as expected. We can extract this offset voltage in such a way that the corrected Suns-ISC curve shows a linear behavior, i.e. ISC=( V OC ' - D V OFST ) / R sh . In the example shown in Figure S2(b), we obtain
DVOFST = 2.07mV . Given the “corrected Suns-ISC” curve one can calculate the ISC /Sun factor and calculate the ISC for any sun intensity as shown in the right scale of Figure S2(a), thus obtaining the ISC-VOC plot. To minimize the voltage offset effect we could use higher Rsh; however this may distort the Suns-ISC curve at high light intensity [Figure S2(b)], as the voltage drop across the Rsh becomes comparable with the VOC.
The Suns-VOC measurement has also been repeated for high performance CZTSSe devices with various bandgaps as shown in Figure S3 below. All the devices have carrier density < 1017 /cm3,
2 as detected from drive level capacitance profiling technique31. In all curves we observe the
Suns-VOC bending behavior.
Figure S3. High intensity Suns-VOC curves of CZTSSe cells with increasing bandgap. The solid circles indicate inflection points where the ideality factor (nS) is zero.
B. Low intensity Suns-VOC (<1 sun) measurement using Continuous Neutral Density Filter (CNDF)
Besides using the Sinton tool we have also developed a technique to perform in-situ Suns-VOC measurement in a standard solar simulator as shown in Figure S4(a) thus allowing an immediate comparison of the JSC-VOC curves and the standard light and dark J-V curves. This system also allows low temperature measurements of the JSC-VOC curves using the same solar simulator.
For the Suns-VOC sweep the solar simulator maintains a constant 1 sun output and its intensity is attenuated by using a special, custom-made large area continuous neutral density filter (CNDF) as described in Ref. 13. Large area CND filters are not commercially available; thus we fabricate them in-house using ink-jet printing on a common overhead projector transparency sheet. We first draw the radial gray scale pattern, print it and mount it on a black acrylic frame as shown in the inset of Figure S4(b). The filter is mounted on a stepper motor gearbox and can be rotated by a computer-controlled motor controller. The program is implemented in MATLAB.
For JSC-VOC measurement, the system sets the baseline sun intensity to 1 sun and starts the CND filter at the open area position yielding the unattenuated, 1 sun illumination on the solar cell. The motor box then rotates the CND filer slowly towards the darker region and the system -4 captures both JSC and VOC at every light intensity. We can achieve dynamic range of 1 to 10 sun using this setup and the JSC-VOC data can be obtained with fine resolution for accurate ideality factor, nS, extraction. The ideality factor nS is extracted from the asymptotic slope at the highest data point (at 1 sun) using Eq. 1.
3 The advantage of having an integrated JSC-VOC setup into the existing solar simulator station is that we can measure the standard Light-J-V and JSC-VOC data in one sitting. This is not possible if the sun-VOC curve is captured in a separate system (e.g. the Sinton tool). Furthermore the measurement can also be conducted with a small cryostat to obtain temperature dependent Suns- VOC measurement as presented in Fig. 2.
-4 Figure S4. (a) Low intensity (10 – 1 sun) Suns-VOC setup integrated into the standard solar simulator. (b) Sample Suns-VOC or JSC-VOC data for CZTSSe cell “Z1” and a CIGSSe cell “G1”. Inset: The radial CNDF that allows continuous light attenuation from 1 to ~10-4 sun.
We can compare this “CNDF” technique and the Sinton’s tool Suns-VOC measurement that we describe previously as shown in Figure S5. We observe that all measurements are consistent except they cover different ranges. This comparison also allows us to measure the absolute “sun” intensity at the solar cell in the Sinton tool by using the JSC at 1 sun measured from the solar simulator (JSC-VOC data).
10 Figure S5. Comparison of Suns-VOC (JSC-VOC) measurements using the Sinton’s tool and the CNDF technique13.
4 C. Device Simulation Model
Device simulation model parameters for wxAMPS simulation16 in Section IV are presented in Table S1. The absorber model “A0” is the baseline CIGS model18 used to study bulk conductivity effect to Suns-Voc curve (Fig. 4) while absorber model A1 and A2 are used to compare the Suns-Voc characteristics in a clean absorber vs. defected one (Fig. 5). A more detailed device model specific for a high performance CZTSSe cell can be found in Ref. 32.
Symbol Unit ZnO CdS Absorber
LAYER PROPERTIES
Width w nm 200 50 3000
Dielectric constant ε r 9 10 13.6 Affinity eV 4.4 4.2 4.5 2 Electron mobility e cm /Vs 100 100 100 2 Hole mobility p cm /Vs 25 25 25 3 18 18 Donor density ND /cm 10 1.110 0 3 16 Acceptor density NA /cm 0 0 210
Bandgap Eg eV 3.3 2.4 1.15 3 18 18 18 Effective density NC /cm 2.210 2.210 2.210 of states CB+ 3 19 19 19 Effective density NV /cm 1.810 1.810 1.810 of states VB+ ++ CB offset EC eV -0.2 +0.3
DEFECT PROPERTY Model A0 A1 A2 * 3 17 18 14 16 Defect density NDG, NAG /cm D: 10 A:10 D: 10 - D:210 Gaussian Gaussian Gaussian Discrete
Energy peak EA, ED eV midgap midgap midgap - 0.5 position**
Energy distribution WG eV 0.1 0.1 0.1 - - width 2 -12 -17 -13 -15 Capture cross e cm 10 10 510 - 10 section e 2 -15 -12 -15 -15 Capture cross h cm 10 10 10 - 10 section h
Table S1. Device parameters used for the wxAMPS simulation based on a CIGSSe baseline model18. +CB (VB) is the conduction (valence) band. ++CB offset is the difference in CB with the
5 adjacent layer. *Defect can be donor-like (D) or acceptor-like (A). **Energy peak position is measured with respect to conduction (valence) band for donor (acceptor)-like defect.
D. Ideality factor in a clean semiconductor solar cell
Here we derive the ideality factor of a solar cell made of clean semiconductor with no defect states in the bandgap. The VOC is related to the quasi Fermi level separation at the front and the back contact:
VOC= E Fn - E Fp S(1)
The hole EFp is mainly determined by the doping density:
EFp= E i - k B Tln[( NA + D n ) / n i ] S(2)
where ni is the intrinsic carrier concentration and Ei is the intrinsic Fermi level.
The electron EFn will be mainly controlled by the light intensity. Here we have the generation rate proportional to the light intensity (or concentration factor S): G= c1 S , where c1 is an arbitrary constant. Starting from Eq. 3, assuming a constant lifetime and clean density of states: g( E ) � E EC we have:
1g ( E ) G( S ) = R = dE , S(3) 0 1+ exp[(E - EFn ) / k B T ]t ( E , n )
G( S )= c1 S = ni exp[( E Fn - E i ) / k B T ]/t = D n / t S(4)
EFn= E i + k B Tln( D n / n i ) S(5)
k T where Dn is the excess photogenerated electron density. Using Eq. S(1) we have: V = B OC q 骣 骣 (NA+ D n ) D n k B T NA D n ln琪2 ln 琪 2 since NA >> D n . From Eq. S(4) : Dn = c1 St and using 桫niq 桫 n i -1 Eq. 1: nS= [ V T dln S / dV OC ] , we obtain nS = 1.
6 E. Circuit Model with Back Contact Diode
In a solar cell device with non-ohmic back contact, the device can be modeled as a standard solar cell junction “PV” and a parasitic back contact junction “BC” shunted by a shunt resistance RBC as shown in Fig. 7(a). We can model the Suns-VOC behaviors of CZTSSe devices using the following relationships:
骣S J L1 A VOC( S )= V OCA - V OCB = n1 A V T ln琪 + 1 - V OC , B S(6) 桫 J 0 A
S JL1 B= J 0 B[exp( V OCB / n 1 B V T ) - 1] + V OCB / R BC , S(7) where subscript A refers to the primary photovoltaic (PV) diode and B refers to the parasitic back contact diode. From the last equation we can solve for VOCB numerically as:
VOCB= f( S , J L1 B , J 0 B , n 1 B , R BC ) .
We can fit this model into the experimental data as shown in Fig. 7. There are five independent parameters involved: JL1 A/ J 0 A , n1A, JL1 B/ J 0 B , n1B and RBC. First we extract JL1 A/ J 0 A and n1A from the low sun intensity regime (S < 1 sun) and then JL1 B/ J 0 B and n1B from the high intensity regime by fitting VOC- V OCA vs. S. In devices with poor back contact normally the RBC is not 2 small (> 1 .cm ) and should be in order of the series resistance (RS) of the device (if RBC is very small that means the back contact is good or ohmic). The Suns-VOC curve is not very 2 sensitive to RBC when it is large (> 1 .cm ) [see Fig. 7(c)]. We could check the curve fitting result by substituting RBC ~ RS and observe almost no change in the calculated Suns-VOC curve. 29,30 (For device Z2 using Sites’ method for diode parameter extraction we obtain RS = 4.8 .cm2).
For the data as shown in Fig. 6(b) and performing a numerical curve-fitting, we obtain: 9 2 n1A = 0.82 , JL1 A/ J 0 A = 4.0 10 , n1B = 1.7 and JL1 B/ J 0 B = 0.71 and RBC ~5 .cm . These parameters provide a good fit to the experimental data as shown in Fig. 7(a). We observe that the dark reverse saturation current of the back contact (J0B) is much larger (relative to its photocurrent JL1A) than that of the primary PV diode (J0A), indicating that this junction is very leaky–which is expected for a junction that is originally intended to be an ohmic contact.
REFERENCES
31 J. T. Heath, J. D. Cohen, and W. N. Shafarman, J. Appl. Phys. 95, 1000 (2004). 32 T. Gokmen, O. Gunawan, D. B. Mitzi, Appl. Phys. Lett. 105, 033 903 (2014).
7