The Definite Integrals

Definite Integrals Advanced Level Pure Mathematics Definite Integrals 1 Properties of Definite Integrals 3 Integration by Parts 4 Continuity and Differentiability of a Definite Integral 5 Improper Integrals 6

Definite Integrals

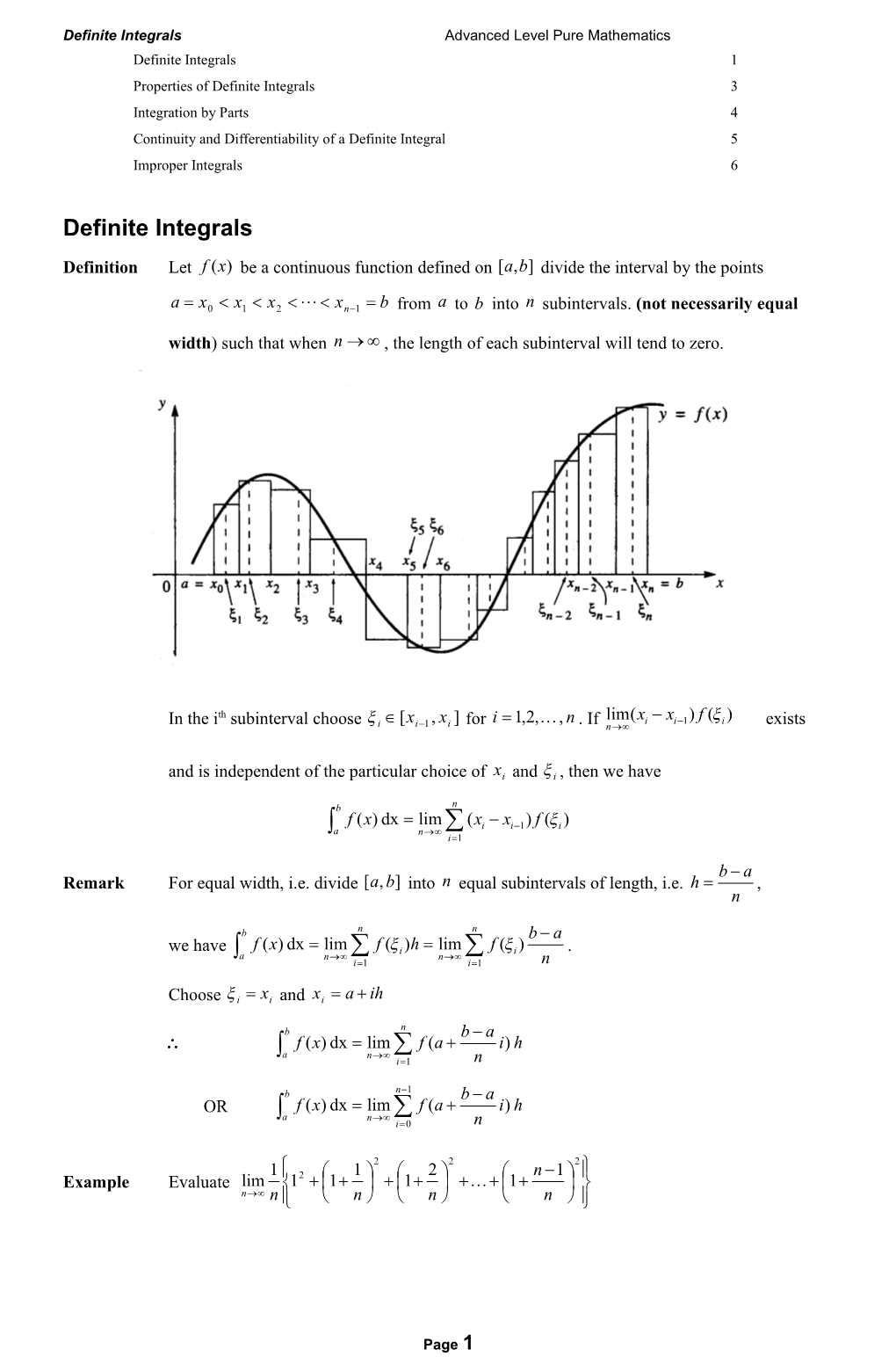
Definition Let f (x) be a continuous function defined on [a,b] divide the interval by the points

a  x0  x1  x2  ⋯  xn1  b from a to b into n subintervals. (not necessarily equal

width) such that when n   , the length of each subinterval will tend to zero.

th  [x , x ] i  1,2,, n lim(xi  xi1) f (i ) In the i subinterval choose i i1 i for . If n exists

and is independent of the particular choice of xi and  i , then we have

b n f (x) dx  lim (xi  xi1) f (i ) a n  i1

b  a Remark For equal width, i.e. divide [a, b] into n equal subintervals of length, i.e. h  , n

b n n b  a we have f (x) dx  lim f (i )h  lim f (i ) . a n  n  i1 i1 n

Choose  i  xi and xi  a  ih

b n b  a  f (x) dx  lim f (a  i) h a n  i1 n

b n1 b  a OR f (x) dx  lim f (a  i) h a n  i0 n

 2 2 2  1  2  1   2   n 1  Example Evaluate lim 1  1   1    1   n n   n   n   n  

Definite Integrals Advanced Level Pure Mathematics

 1 1 1  * Example I = lim  ⋯  n n2  n n2  2n n2  2n2 

1 x x x *AL95II (a) Evaluate  a  b 1 , where a,b  0 . lim  x0 3 

(b) By considering a suitable definite integral, evaluate

 12 22 n2  lim  ⋯   3 3 3 3 3 3  n n 1 n  2 n  n 

dx AL83II-1 Evaluate (a) ,  (x  a)(x  b)

  (b) 4 ln(1 tan x)dx , [ Hint: Put u   x .] 0 4

1   2  (n 1)   *(c) lim cos  cos ⋯ cos  n n  n n n 

Properties of Definite Integrals

P1 The value of the definite integral of a given function is a real number, depending on its lower

and upper limits only, and is independent of the choice of the variable of integration, i.e.

b b b f (x)dx  f (y)dy  f (t)dt . a a a

b a P2 f (x)dx   f (x)dx a b

a b b P3 f (x)dx  f (x)dx  0 dx  0 a b a

b c b P4 Let a  c  b , then f (x)dx  f (x)dx  f (x)dx a a c

P5* Comparison of two integrals

b b If f (x)  g(x) x  (a, b) , then f (x)dx  g(x)dx a a

Example x 2  x , for all x  (0,1) ;

1 1 hence x 2 dx  x dx . 0 0

3  2  2 Example Prove that (a) 2 x sin x dx    . 0 3  2 

  (b) 2 sinn xdx  2 sinn1 xdx 0 0

P6 Rules of Integration

If f (x), g(x) are continuous function on [a, b] then

b b (a) kf (x)dx  k f (x)dx for some constant k. a a

b b b (b)  f (x)  g(x)dx  f (x)dx  g(x)dx . a a a

a a P7* (a) f (x)dx  f (a  x)dx . a : any real constant. 0 0

a a (b) f (x) dx   f (x)  f (x) dx . a 0

2a a (c) f (x)dx   f (x)  f (2a  x) dx 0 0

b b (d) f (x)dx  f (a  b  x)dx a a

Exercise 7C

a a 1. * By proving that f (x)dx  f (a  x)dx (7c5) 0 0

  sin x evaluate (a) 2 (cos x  sin x)1997 dx (b) 2 dx 0 0 sin x  cos x

a a 2 (a) Show that f (x) dx   f (x)  f (x) dx (7c6) a 0

(b) Using (a), or otherwise, evaluate the following integrals:

 1 4 d 2 (i)  (iii) ln(x  1 x )dx  1 4 1 sin

Remind sin x,ex  e x are odd functions.

1 cos x, are even functions. x2 1

Definite Integrals Advanced Level Pure Mathematics Graph of an odd function Graph of an even function

P8 (i) If f (x)  f (x) (Even Function)

a a then f (x) dx  2 f (x) dx a 0

(ii) If f (x)   f (x) (Odd Function)

a then f (x) dx  0 a

Definition Let S be a subset of R , and f (x) be a real-valued function defined on S . f (x) is called a

PERIODIC function if and only if there is a positive real number T such that f (x  T)  f (x) ,

for x  S . The number T is called the PERIOD.

P9 If f (x) is periodic function, with period T i.e. f (x  T)  f (x)

  T (a) f (x)dx  f (x)dx   T

  T (b) f (x)dx  f (x)dx 0 T

T  T (c) f (x)dx  f (x)dx  0

nT T (d) f (x) dx  n f (x) dx for n  Z  0 0

Theorem Cauchy-Inequality for Integration

If f (x) , g(x) are continuous function on [a,b] , then

b 2  b 2  b 2   f (x)g(x)dx    f (x) dx g(x) dx  a   a  a 

Theorem Triangle Inequality for Integration

b b f (x) dx  f (x) dx a a

Integration by Parts

Theorem Integration by Parts

Let u and v be two functions in x . If u'(x) and v'(x) are continuous on a,b, then

b b b uv'dx  uv  vu'dx a a a

b b b or udv  uv  vdu a a a

 sin kx * AL84II-1 (a) For any non-negative integer k, let uk  dx . 0 sin x

Express uk 2 in terms of uk .

Hence, or otherwise, evaluate uk .

 (b) For any non-negative integers m and n , let I(m,n)  2 cosm  sin n dθ 0

(i) Show that if m  2 , then

 m 1 I(m,n) =   I(m  2, n  2) .  n 1  (ii) Evaluate I(1,n) for n  0 .

(iii) Show that if n  2 , then

 n 1 I(0,n) =   I(0,n  2) .  n  (iv) Evaluate I(6,4) .

 AL94II-11 For any non-negative integer n , let 4 n In  tan x dx 0

n1 1   1   (a) (i) Show that    In    . n 1  4  n 1  4 

4x  [ Note: You may assume without proof that x  tan x  for x [0, ] . ]  4

lim In (ii) Using (i), or otherwise, evaluate n .

1 (iii) Show that I  I  for n  2,3,4,. n n2 n 1

n (1)k 1  (b) For n  1,2,3, , let an   . k 1 2k 1

(i) Using (a)(iii), or otherwise, express an in terms of I 2n .

lim an (ii) Evaluate n .

Definite Integrals Advanced Level Pure Mathematics Continuity and Differentiability of a Definite Integral

Theorem Mean Value Theorem for Integral

If f (x) is continuous on [a,b] then there exists some c in [a,b] and

b f (x)dx  f (c)(b  a) a

Theorem Continuity of definite Integral

x If f (t) is continuous on a,band let A(x)  f (t)dt x [a,b] then A(x) is continuous at a

each point x in a,b .

Theorem * Fundamental Theorem of Calculus

x Let f (t) be continuous on [a,b] and F(x)  f (t)dt . Then F'(x)  f (x) , x  (a,b) a

g(x) Remark : H (x)  f (t)dt  H '(x)  f (g(x)) g'(x) a

Example Let f : R  R be a function which is twice-differentiable and with continuous second

x t derivative. Show that f (x)  f (0)  xf '(0)   f ''(s)dsdt , x  R . 0  0 

d x n * AL90II-5 (a) Evaluate f (t) dt , where f is continuous and n is a positive integer. dx 0

2 x 2 (b) If F(x)  et dt , find F '(1). x3

x  1 t 2 1  AL97II-5(b) Evaluate lim  3 e dt  2  . x0  x 0 x 

AL98II-2 Let f : R  R be a continuous periodic function with period T .

d xT x (a) Evaluate  f (t)dt  f (t)dt dx  0 0 

xT T (b) Using (a), or otherwise, show that f (t)dt  f (t)dt for all x . x 0

Improper Integrals

b Definition A definite integral f (x)dx is called IMPROPER INTEGRAL if the interval [a,b] of a

integration is infinite, or if f (x) is not defined or not bounded at one or more points in [a,b].

 1  1  x   1 Example e dx , x 2 , tan xdx , dx are improper integral. e dx 0 2 0  0 x

 b Definition (a) f (x)dx is defined as lim f (x)dx a b a

b b (b) f (x)dx is defined as lim f (x)dx  a a

 c  (c) f (x)dx is defined as f (x)dx  f (x)dx for any real number c .  - c

c ℓ ( Or lim f (x)dx  lim f (x)dx ) ℓ ℓ ℓc

(d) If f (x) is continuous except at a finite number of points, say a, x1, b where

b a  x1  b , then f (x)dx is defined to be a

c ℓ d ℓ lim f (x)dx  lim f (x)dx  lim f (x)dx  lim f (x)dx  ℓ  c  ℓ  d ℓa ℓx1 ℓx1 ℓb

for any c,d such that a  c  x1  d  b .

Definition The improper integral is said to be Convergent or Divergent according to the improper

integral exists or not.

Theorem Let f (x) and g(x) be two real-valued function continuous for x  a . If 0  f (x)  g(x)

  x  a then the fact that f (x)dx diverges implies g(x)dx diverges and the fact that a a

  g(x)dx converges implies that f (x)dx converges. a a

Definite Integrals Advanced Level Pure Mathematics Example Determine whether the improper integrals are convergent or divergent.

0 a) xe x dx (p.109 7-45c) 

2 dx b) 2 2 (p.112 7-50 b) 4 - x

1 dx c) (p.112 7-50 c) 1 x 2