DOCSLIB.ORG

Symplectic Lanczos for Hamiltonian-Positive Matrices Encounters No Serious Breakdown!)

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Symplectic Lanczos for Hamiltonian-Positive Matrices Encounters No Serious Breakdown!) GAMM Annual Meeting 2013 Novi Sad, March 18{22, 2013 THE SYMPLECTIC LANCZOS PROCESS FOR HAMILTONIAN-POSITIVE MATRICES (Symplectic Lanczos for Hamiltonian-positive matrices encounters no serious breakdown!) Peter Benner Max Planck Institute for Dynamics of Complex Technical Systems Computational Methods in Systems and Control Theory Magdeburg, Germany TU Chemnitz Mathematics in Industry and Technology Chemnitz, Germany Joint work with Ahmed Salam (ULCO, Calais) Introduction Symplectic Lanczos Hamiltonian-positiv References Introduction Hamiltonian Eigenproblems Definition 0 In Let J = , then H 2 R2n×2n is called Hamiltonian if −In 0 (HJ)T = HJ. Note: J−1 = JT = −J. Explicit block form of Hamiltonian matrices AB ; where A; B; C 2 n×n and B = BT ; C = C T : C −AT R Max-Planck-Institut Magdeburg Peter Benner, Symplectic Lanczos for Hamiltonian-positive matrices 2/13 Introduction Symplectic Lanczos Hamiltonian-positiv References Introduction Hamiltonian Eigenproblems Definition 0 In Let J = , then H 2 R2n×2n is called Hamiltonian if −In 0 (HJ)T = HJ. Note: J−1 = JT = −J. Explicit block form of Hamiltonian matrices AB ; where A; B; C 2 n×n and B = BT ; C = C T : C −AT R Max-Planck-Institut Magdeburg Peter Benner, Symplectic Lanczos for Hamiltonian-positive matrices 2/13 Typical Hamiltonian spectrum Introduction Symplectic Lanczos Hamiltonian-positiv References Introduction Spectral Properties Hamiltonian Eigensymmetry Hamiltonian matrices exhibit the Hamiltonian eigensymmetry: if λ is a finite eigenvalue of H, then λ,¯ −λ, −λ¯ are eigenvalues of H, too. Max-Planck-Institut Magdeburg Peter Benner, Symplectic Lanczos for Hamiltonian-positive matrices 3/13 Introduction Symplectic Lanczos Hamiltonian-positiv References Introduction Spectral Properties Hamiltonian Eigensymmetry Hamiltonian matrices exhibit the Hamiltonian eigensymmetry: if λ is a finite eigenvalue of H, then λ,¯ −λ, −λ¯ are eigenvalues of H, too. Typical Hamiltonian spectrum Max-Planck-Institut Magdeburg Peter Benner, Symplectic Lanczos for Hamiltonian-positive matrices 3/13 Introduction Symplectic Lanczos Hamiltonian-positiv References Hamiltonian Eigenproblems Goal Structure-preserving algorithm, i.e., if λ~ is a computed eigenvalue of H, then λ,~ −λ,~ −λ~ should also be computed eigenvalues. Goal cannot be achieved by general methods for matrices or matrix pencils like the QR/QZ, Lanczos, Arnoldi algorithms! For an algorithm based on similarity transformations, the goal is achieved if the Hamiltonian structure is preserved. Definition V 2 R2n×2n is symplectic if V T JV = J, i.e., V −1 = JT V T J. 2n×2k T Vk 2 R is symplectic or a J-isometry if Vk JnVk = Jk : Lemma If H is Hamiltonian and V is symplectic, then V −1HV is Hamiltonian, too. Max-Planck-Institut Magdeburg Peter Benner, Symplectic Lanczos for Hamiltonian-positive matrices 4/13 Introduction Symplectic Lanczos Hamiltonian-positiv References Hamiltonian Eigenproblems Goal Structure-preserving algorithm, i.e., if λ~ is a computed eigenvalue of H, then λ,~ −λ,~ −λ~ should also be computed eigenvalues. Goal cannot be achieved by general methods for matrices or matrix pencils like the QR/QZ, Lanczos, Arnoldi algorithms! For an algorithm based on similarity transformations, the goal is achieved if the Hamiltonian structure is preserved. Definition V 2 R2n×2n is symplectic if V T JV = J, i.e., V −1 = JT V T J. 2n×2k T Vk 2 R is symplectic or a J-isometry if Vk JnVk = Jk : Lemma If H is Hamiltonian and V is symplectic, then V −1HV is Hamiltonian, too. Max-Planck-Institut Magdeburg Peter Benner, Symplectic Lanczos for Hamiltonian-positive matrices 4/13 Introduction Symplectic Lanczos Hamiltonian-positiv References Hamiltonian Eigenproblems Goal Structure-preserving algorithm, i.e., if λ~ is a computed eigenvalue of H, then λ,~ −λ,~ −λ~ should also be computed eigenvalues. Goal cannot be achieved by general methods for matrices or matrix pencils like the QR/QZ, Lanczos, Arnoldi algorithms! For an algorithm based on similarity transformations, the goal is achieved if the Hamiltonian structure is preserved. Definition V 2 R2n×2n is symplectic if V T JV = J, i.e., V −1 = JT V T J. 2n×2k T Vk 2 R is symplectic or a J-isometry if Vk JnVk = Jk : Lemma If H is Hamiltonian and V is symplectic, then V −1HV is Hamiltonian, too. Max-Planck-Institut Magdeburg Peter Benner, Symplectic Lanczos for Hamiltonian-positive matrices 4/13 Introduction Symplectic Lanczos Hamiltonian-positiv References Introduction Applications Hamiltonian eigenproblems arise in many different applications, e.g.: Systems and control: Solution methods for algebraic and differential Riccati equations. Design of LQR/LQG/H2/H1 controllers and filters for continuous-time linear control systems. Stability radii and system norm computations; optimization of system norms. Passivity-preserving model reduction based on balancing. Reduced-order control for infinite-dimensional systems based on inertial manifolds. Computational physics: exponential integrators for Hamiltonian dynamics. [Eirola '03, Lopez/Simoncini '06, B./Meister '13] Quantum chemistry: computing excitation energies in many-particle systems using random phase approximation (RPA). Quadratic eigenvalue problems: in particular, gyroscopic systems. Max-Planck-Institut Magdeburg Peter Benner, Symplectic Lanczos for Hamiltonian-positive matrices 5/13 Introduction Symplectic Lanczos Hamiltonian-positiv References The Symplectic Lanczos Algorithm Symplectic Lanczos Algorithm for Hamiltonian operators H is based on transpose-free unsymmetric Lanczos process [Freund '94]; computes partial J-tridiagonalization; 2n×2k provides a symplectic (J-orthogonal) Lanczos basis Vk 2 R , T i.e., Vk JnVk = Jk ; was derived in several variants: [Freund/Mehrmann '94, Ferng/Lin/Wang '97, B./Faßbender '97, Watkins '04]; requires re-J-orthogonalization using, e.g., modified symplectic Gram-Schmidt; can be restarted implicitly using implicit SR steps [B./Faßbender '97] or Krylov-Schur restarting [B./Faßbender/Stoll '11] which allows easy locking & purging procedure; does not provide an orthogonal Lanczos basis and is prone to serious breakdown. Max-Planck-Institut Magdeburg Peter Benner, Symplectic Lanczos for Hamiltonian-positive matrices 6/13 Introduction Symplectic Lanczos Hamiltonian-positiv References The Hamiltonian J-Tridiagonal Form or Hamiltonian J-Hessenberg Form 2 δ1 β1 ζ2 3 6 δ2 ζ2 β2 ζ3 7 6 7 6 .. .. 7 6 δ ζ . 7 6 3 3 7 6 . 7 6 . 7 6 . ζn 7 6 7 2n×2n Tn = 6 δn ζn βn 7 2 R ; 6 7 6 ν1 −δ1 7 6 7 6 ν2 −δ2 7 6 7 6 ν3 −δ3 7 6 7 6 . 7 4 .. .. 5 νn −δn −1 can be computed by symplectic similarity Tn = V HV for almost (serious breakdown!) any V1 = V (:; 1), is computed partially by symplectic Lanczos process, based on symplectic Lanczos recursion T HVk = Vk Tk + ζk+1vk+1e2k ; Vk = [V (:; 1 : k); V (:; n + 1 : n + k)]: Max-Planck-Institut Magdeburg Peter Benner, Symplectic Lanczos for Hamiltonian-positive matrices 7/13 Introduction Symplectic Lanczos Hamiltonian-positiv References The Symplectic Lanczos Algorithm T Algorithm based on symplectic Lanczos recursion HVk = Vk Tk + ζk+1vk+1e2k 2n×2n 2n INPUT: H 2 R , k 2 N, and start vectorv ~1 6= 0 2 R . 2k×2k 2n×2k OUTPUT: Tk 2 R , Vk 2 R , ζk+1, and vk+1. 1 ζ1 = kv~1k2 1 2 v1 = v~1 ζ1 3 FOR m = 1; 2;:::; k (a) t = Hvm (b) δm = ht; vmi % B./Faßbender '97: δm = 1, Watkins '04: δm = 0. (c)~wm = t − δmvm (d) νm = ht; vmiJ 1 (e) wm = w~m νm (f) u = Hwm (g) βm = −hu; wmiJ (h)~vm+1 = u − ζmvm−1 − βmvm + δmwm (i) ζm+1 = kv~m+1k2 1 (j) vm+1 = v~m+1 ζm+1 ENDFOR Note: 3(b) yields orthogonality of vk ; wk [Ferng/Lin/Wang '97] and optimal conditioning of Lanczos basis [B. '03] if kvk2 = 1 is forced. Max-Planck-Institut Magdeburg Peter Benner, Symplectic Lanczos for Hamiltonian-positive matrices 8/13 Introduction Symplectic Lanczos Hamiltonian-positiv References The Symplectic Lanczos Algorithm T Algorithm based on symplectic Lanczos recursion HVk = Vk Tk + ζk+1vk+1e2k 2n×2n 2n INPUT: H 2 R , k 2 N, and start vectorv ~1 6= 0 2 R . 2k×2k 2n×2k OUTPUT: Tk 2 R , Vk 2 R , ζk+1, and vk+1. 1 ζ1 = kv~1k2 1 2 v1 = v~1 ζ1 3 FOR m = 1; 2;:::; k (a) t = Hvm (b) δm = ht; vmi % B./Faßbender '97: δm = 1, Watkins '04: δm = 0. (c)~wm = t − δmvm (d) νm = ht; vmiJ 1 (e) wm = w~m νm (f) u = Hwm (g) βm = −hu; wmiJ (h)~vm+1 = u − ζmvm−1 − βmvm + δmwm (i) ζm+1 = kv~m+1k2 1 (j) vm+1 = v~m+1 ζm+1 ENDFOR Note: 3(b) yields orthogonality of vk ; wk [Ferng/Lin/Wang '97] and optimal conditioning of Lanczos basis [B. '03] if kvk2 = 1 is forced. Max-Planck-Institut Magdeburg Peter Benner, Symplectic Lanczos for Hamiltonian-positive matrices 8/13 Introduction Symplectic Lanczos Hamiltonian-positiv References The Symplectic Lanczos Algorithm Numerical example: rolling tire Results from [B./Faßbender/Stoll '08/'11] Modeling the noise of rolling tires requires to determine the transient vibrations, [Nackenhorst/von Estorff '01]. FEM model of a deformable wheel rolling on a rigid plane surface results in a gyroscopic system of order n = 124; 992 [Nackenhorst '04]. Here, use reduced-order model of size n = 2; 635 computed by AMLS [Elssel/Voß '06]. Max-Planck-Institut Magdeburg Peter Benner, Symplectic Lanczos for Hamiltonian-positive matrices 9/13 Introduction Symplectic Lanczos Hamiltonian-positiv References The Symplectic Lanczos Algorithm Numerical example: rolling tire Results from [B./Faßbender/Stoll '08/'11] Compare eigs and symplectic Lanczos with Krylov-Schur restarting (HKS) applied to H−1 to compute the 12 smallest eigenvalues. eigs needs 8, HKS 6 iterations. max(cond (SR)) = 331. Eigenvalues scaled by 1,000. eigs HKS
Load more

Recommended publications
  • Adam of Bremen on Slavic Religion
    Chapter 3 Adam of Bremen on Slavic Religion 1 Introduction: Adam of Bremen and His Work “A. minimus sanctae Bremensis ecclesiae canonicus”1 – in this humble manner, Adam of Bremen introduced himself on the pages of Gesta Hammaburgensis ecclesiae pontificum, yet his name did not sink into oblivion. We know it thanks to a chronicler, Helmold of Bosau,2 who had a very high opinion of the Master of Bremen’s work, and after nearly a century decided to follow it as a model. Scholarship has awarded Adam of Bremen not only with a significant place among 11th-c. writers, but also in the whole period of the Latin Middle Ages.3 The historiographic genre of his work, a history of a bishopric, was devel- oped on a larger scale only after the end of the famous conflict on investiture between the papacy and the empire. The very appearance of this trend in histo- riography was a result of an increase in institutional subjectivity of the particu- lar Church.4 In the case of the environment of the cathedral in Bremen, one can even say that this phenomenon could be observed at least half a century 1 Adam, [Praefatio]. This manner of humble servant refers to St. Paul’s writing e.g. Eph 3:8; 1 Cor 15:9, and to some extent it seems to be an allusion to Christ’s verdict that his disciples quarrelled about which one of them would be the greatest (see Lk 9:48). 2 Helmold I, 14: “Testis est magister Adam, qui gesta Hammemburgensis ecclesiae pontificum disertissimo sermone conscripsit …” (“The witness is master Adam, who with great skill and fluency described the deeds of the bishops of the Church in Hamburg …”).
    [Show full text]
  • Economic Risks Associated with Low Flows in the Elbe River Basin (Germany): an Integrated Economic-Hydrologic Approach to Assess Vulnerability to Climate Change
    IWRM Conference in Dresden 12-13 October 2011 Hamburg Magdeburg Dresden Ústí n. L. Economic risks associated with low flows in the Elbe River Basin (Germany): an integrated economic-hydrologic approach to assess vulnerability to climate change. Malte Grossmann TU Berlin IWRM Conference 12.-13. Oct. 2011 Dresden Grossmann Hamburg Overview Magdeburg 1 / General background Dresden 2/ Approach of the GLOWA Elbe Project Ústí n. L. 3/ Results – assessment of climate risk 4/ Results - cost benefit analysis of adaptation options 5/ Conclusions IWRM Conference 12.-13. Oct. 2011 Dresden Grossmann Hamburg Magdeburg Dresden Ústí n. L. 1 / General background IWRM Conference 12.-13. Oct. 2011 Dresden Grossmann Why develop integrated hydrologic-economic waterHamburg resources models? Magdeburg Dresden Ústí n. L. Management challenges: (a) to develop strategies to minimise economic impact of drought and periodic water shortages (b) to assess basin wide efficiency of water use and to assess instruments to improve efficiency for example by inter-sectoral reallocations in water scarce basins (c) to assess infrastructure investments in terms of benefits and costs in the context of long term water systems planning => to assess the impacts of climate change on the long term performance of water resource system IWRM Conference 12.-13. Oct. 2011 Dresden Grossmann Hamburg Two principal modelling approaches Magdeburg Optimisation Dresden => ability to identify economically efficient water allocations and to analyse Ústí n. L. different institutional mechanisms of water allocation. Simulation ⇒ allow a more detailed analysis of the hydrological processes. ⇒ assessment of the feasibility of management options with regard to infrastructure operations and to identify systems components that have a high risk of failure under extreme conditions.
    [Show full text]
  • Magdeburg - Hamburg (8 Tage)
    Magdeburg - Hamburg (8 Tage) Beschreibung: Dieser Routenverlauf verbindet Sie, dem Strom der Elbe folgend, mit zwei sehr sehens- und erlebenswerten Städten. Sie beginnen Ihre Tour in der sachsen-anhaltischen Landeshauptstadt Magdeburg, die im Jahr 2005 ihr 1200-jähriges Stadtjubiläum beging. Auf dem Elberadweg radeln Sie auf einer der reizvollsten Radwanderrouten Europas Richtung Norden. Lassen Sie Ihren Blick über die weiträumigen Auenlandschaften schweifen und erkunden Sie die Schätze des Biosphärenreservats „Flusslandschaft Elbetal“. Neben der einzigartigen Flusslandschaft durchradeln Sie reizvolle Orte, allen voran die Kaiserstadt Tangermünde und das malerische Elbstädtchen Lauenburg. Den abschließenden Höhepunkt Ihrer Tour bildet die Freie und Hansestadt Hamburg. Hamburg bietet nicht nur viel Sehenswertes und alle Vorzüge einer Metropole, sondern auch einmalige Bedingungen für alle Fahrrad- und Naturbegeisterten. Klicken Sie auf das Bild rechts für weitere Impressionen! Termine: Reisebeginn täglich möglich 01.04. - 31.10.2021 buchbarer Zeitraum: 01.04.2021 - 31.10.2021 Streckenlänge: 353 km Route: Tag 1: Individuelle Anreise nach Magdeburg Heute reisen Sie in Magdeburg an. Die 1200-jährige Landeshauptstadt Sachsen-Anhalts hält viel Sehens- und Erlebenswertes für Sie bereit! Mit zahllosen Parkanlagen, die zu Erholung und Entspannung einladen, ist sie die drittgrünste Stadt Deutschlands. Besuchen Sie den imposanten Dom und das altehrwürdige Kloster Unser Lieben Frauen im Herzen der Stadt. Überall begegnen Ihnen Spuren berühmter Kinder der Stadt, von denen der Physiker Otto von Guericke, der Musiker Georg Phillip Telemann und General von Steuben zu den bekanntesten zählen. Tag 2: Magdeburg - Tangermünde (ca. 73 km) Über den Herrenkrugpark, immer entlang der Elbe, verlassen Sie die Domstadt Richtung Norden. Besichtigen Sie auf Ihrem Weg das modernste Wasserstraßenkreuz Europas mit einer Trogbrücke, die ingenieurtechnisch ihresgleichen sucht.
    [Show full text]
  • Elbe, Magdeburg - Hamburg - Cuxhaven Vom „Magdeburger Reiter“ Zur Hansestadt, Dem „Tor Zur Welt“ Und an Die Nordsee
    Individuell Elbe, Magdeburg - Hamburg - Cuxhaven Vom „Magdeburger Reiter“ zur Hansestadt, dem „Tor zur Welt“ und an die Nordsee Hamburg mit Rathaus und Alster 10. Tag Glückstadt – Cuxhaven Deutschland Die Elbfähre (nicht inkl.) bringt Sie über den Fluss. Sie radeln durch den “Cuxland” genannten Landkreis Cuxhaven, in dem traditionsreiche Badeorte und Seebäder zahlreiche Gäste an die Nordseeküste locken. (ca. 58 km) 11. Tag Cuxhaven Individuelle Abreise oder Verlängerung. Termine Tour EBH/EBC Freitag u. Sonntag Saison 1: 09.04. - 21.05. und 24.08. - 04.10.21 Saison 2: 22.05. - 23.08.21 Termine Tour EH/EC Samstag u. Montag Saison 1: 10.04. - 21.05. und 24.08. - 04.10.21 Saison 2: 22.05. - 23.08.21 (Sondertermine ab 4 Personen auf Anfrage) Reisepreise in EUR pro Person: Tour DZ/ÜF EZZ Die Domstadt Magdeburg ist Startpunkt dieser Radreise. Auf dieser abwechslungsreichen Tour EH, Saison 1 595 175 kommen Sie in das mittelalterliche Tangermünde, nach Havelberg mit dem prächtigen Dom und in EH, Saison 2 635 175 die Fachwerkstadt Hitzacker. Das Biosphärenreservat Flusslandschaft Elbe, die Festung Dömitz, das EBH, Saison 1 675 200 Schloss Bleckede und Lauenburg sind weitere Höhepunkte auf dem Weg zum “Tor zur Welt” und der EBH, Saison 2 715 200 EC, Saison 1 785 225 Elbphilharmonie. Bei der 10 bzw. 11 tägigen Tour radeln Sie weiter bis an die Nordsee. EC, Saison 2 825 225 4. Tag Tangermünde – Havelberg EBC, Saison 1 849 250 Individuelle Touren, ca. 350/460 km EBC, Saison 2 879 250 EH/EBH: 8/9 Tage / 7/8 Nächte Die Radeltour durch das Naturschutzgebiet “Alte Leihrad 7-/21-Gang, EH/EBH 79/85 Magdeburg - Hamburg Elbe” führt Sie vorbei am Schloss Storkau nach Leihrad 7-/21-Gang EC/EBC 89/95 EC/EBC: 10/11 Tage / 9/10 Nächte Havelberg, der “Insel- und Domstadt im Grünen” Elektrorad, EH/EBH 189/199 Magdeburg - Hamburg - Cuxhaven am Zusammenfluss von Havel und Elbe.
    [Show full text]
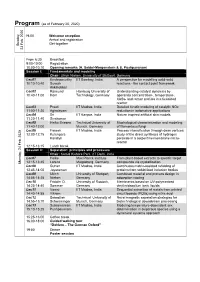
  • Program (As of February 20, 2020)
    Program (as of February 20, 2020) 19:00 Welcome reception Arrival and registration Get-together Sunday, 23 Feb. Feb. 2020 23 From 6:30 Breakfast 9:00-10:00 Registration 10:00-10:10 Opening remarks (A. Seidel-Morgenstern & S. Pushpavanam) Session I: Fundamentals and modeling Chair: Ulrich Nieken, University of Stuttgart, Germany Lec01 Krishnamurthy IIT Bombay, India A perspective for modelling solid-solid 10:10-10:40 Suresh reactions - the contact point framework Akkihebbal Lec02 Raimund Hamburg University of Understanding catalyst dynamics by 10:40-11:00 Horn Technology, Germany operando concentration-, temperature-, XASs- and raman profiles in a fixed-bed reactor Lec03 Preeti IIT Madras, India Detailed kinetic modeling of catalytic NOx 11:00-11:20 Aghalayam reduction in automotive applications Lec04 Sri IIT Kanpur, India Nature inspired artificial skin models 11:20-11:40 Sivakumar Lec05 Heiko Briesen Technical University of Mophological characterization and modeling 11:40-12:00 Munich, Germany of filamentous fungi Lec06 Faseeh IIT Madras, India Process intensification through dean vortices: 12:00-12:15 Kulangara study of the direct synthesis of hydrogen Kandiyil peroxide in a serpentine membrane micro- reactor 12:15-13:15 Lunch break Session II: Separation: principles and processes Chair: Kamal Kishore Pant, IIT Dehli, India Lec07 Heike Max Planck Institute From plant-based extracts to specific target Monday, 24 Feb. 2020 Feb. 24 Monday, 13:15-13:45 Lorenz Magdeburg, Germany compounds via crystallization Lec08 Guhan IIT Madras, India Continuous matrix-assisted refolding of 13:45-14:05 Jayaraman proteins from solubilized inclusion bodies Lec09 Ulrich University of Stuttgart, Combined material and process design in 14:05-14:25 Nieken Germany adsorption cooling Lec10 Fridolin O.
    [Show full text]
  • Assistive Technologies: Companion Or Controller? Appropriation Instead of Instruction
    Assistive technologies: companion or controller? Appropriation instead of instruction Tina HAASE Fraunhofer Institute for Factory Operation and Automation IFF Sandtorstr. 22, 39106 Magdeburg, Germany Wilhelm TERMATH Otto von Guericke University Magdeburg, Department of Vocational Education and Human Resources Development Zschokkestr. 32, 39104 Magdeburg, Germany Dirk BERNDT Fraunhofer Institute for Factory Operation and Automation IFF 39106 Magdeburg, Germany Michael DICK Otto von Guericke University Magdeburg, Department of Vocational Education and Human Resources Development Zschokkestr. 32, 39104 Magdeburg, Germany ABSTRACT1 1. DIGITAL ASSISTIVE TECHNOLOGIES Assistive digital technologies support employees in coping Digital cognitive assistance systems already support the with complex activities by providing the necessary infor- employee in many areas of work [1]. In the field of mainte- mation directly related to the work task and according to nance, the employee requests status data of complex tech- the individual requirements. On the one hand, they have nical systems, opens the latest maintenance documents for the potential to relieve people at work, for example by sup- a malfunctioning component in the work situation, and re- porting physical assistance systems in physically demand- ceives information about the machine and the colleague ing activities. Cognitive assistance systems can achieve re- who conducted the last maintenance [2]. lief by preparing complex data in a way that is comprehen- In the commissioning department, the warehouse employ- sible to the employee and supporting him in carrying out ees are guided using data glasses and pick-by-light. his work and in making decisions. On the other hand, as- In manual assembly, assistance systems are used to sup- sistance systems can lead to expropriation and alienation port the worker in the assembly of increasingly diversified by depriving employees of autonomy and room for maneu- products.
    [Show full text]
  • Application of the Process Modeling Tool Promot to the Modeling of Metabolic Networks
    APPLICATION OF THE PROCESS MODELING TOOL PROMOT TO THE MODELING OF METABOLIC NETWORKS M. Ginkel1, A. Kremling1, F. Tr¨ankle2, E. D. Gilles1,3, and M. Zeitz3 1 Max-Planck-Institut f¨urDynamik komplexer technischer Systeme, Zenit-Geb¨aude Leipziger Str. 44, D-39120 Magdeburg, Phone: +49 391 6117 563, E-mail: [email protected] 2 ETAS GmbH & Co. KG, Stuttgart, Germany. 3 Institut f¨urSystemdynamik und Regelungstechnik, Universit¨atStuttgart, Germany. Abstract. The process modeling tool ProMoT [6, 5] has been developed for the object-oriented and equation-based modeling of chemical processes. This contribution presents the application of ProMoT to a novel application field: the design and implementation of a knowledge base for modeling metabolic networks in living cells. This knowledge base contains predefined modeling entities for the hierarchical aggregation of complex reaction network models. The principles of defining primitive metabolic entities as well as the construction of a flexible knowledge base for modeling larger metabolic networks are presented. Key words: computer-aided process modeling, knowledge base design, object-oriented modeling lan- guage, process modeling tool, metabolic processes 1 Introduction Today commercially and freely available software tools for the steady-state and dynamic simulation of chemical and biological processes are well established in the process engineering community. Whereas these simulation tools provide state-of-the-art numerical methods, the computer-aided development, im- plementation, and reuse of mathematical models for chemical and bioengineering processes are not suffi- ciently supported. The process modeling tool ProMoT has been designed for the computer-aided mod- eling of chemical processes as well as for the implementation of knowledge bases that contain reusable modeling entities [5, 6].
    [Show full text]
  • Cities of Tomorrow Challenges, Visions, Ways Forward
    EN Cities of tomorrow Challenges, visions, ways forward October 2011 Europe Direct is a service to help you find answers to your questions about the European Union Freephone number (*): 00 800 6 7 8 9 10 11 (*) Certain mobile telephone operators do not allow access to 00 800 numbers or these calls may be billed. Copyrights: Cover: © ZAC DE BONNE - AKTIS ARCHITECTURE - Chapter 1: © iStockphoto Page 6: © EC - Page 9: © PHOTOGRAPHIEDEPOT Frank-Heinrich Müller - Chapter 2: © Tova Svanfeldt Page 15: © Corinne Hermant - Page 17: © iStockphoto - Page 20: © Krisztina Keresztely Page 23: © Carmen Vossen - Chapter 3: © Iván Tosics - Page 36: © iStockphoto - Page 37: © iStockphoto Page 41: © Henrik Johansson - Page 42: © La Citta Vita - Page 46: © EC - Page 47: © iStockphoto Page 53: © Anja Schlamann - Page 54: © Marie Schmerkova - Page 59: © iStockphoto - Chapter 4: © Iván Tosics Page 67: © Iván Tosics - Page 73: © iStockphoto - Page 77: © Bernard_in_va Page 82: © "Fragment de Tags" http://fragmentdetags.net/ - Page 83: © W. Vainqueur Conclusions: © City of Växjö © European Union, 2011 Reproduction is authorised provided the source is acknowledged. ISBN: 978-92-79-21307-6 doi:10.2776/41803 European Commission, Directorate General for Regional Policy Unit C.2 - Urban Development, Territorial Cohesion Wladyslaw Piskorz E-mail: [email protected] Internet: http://ec.europa.eu/regional_policy/conferences/citiesoftomorrow/index_en.cfm Unit B.1 – Communication, Information, Relations with Third Countries Raphaël Goulet Avenue de Tervuren 41 B - 1040 Brussels Fax: +32 22966003 E-mail: [email protected] Internet: http://ec.europa.eu/regional_policy/index_en.htm The opinion expressed in this publication do not necessarily reflect the views of the European Commission.
    [Show full text]
  • Germany – Elbe from Dresden to Magdeburg Bike Tour 2021 Individual Self- Guided 8 Days / 7 Nights
    Germany – Elbe from Dresden to Magdeburg Bike Tour 2021 Individual Self- Guided 8 days / 7 nights You arrive in the Florence of the Elbe, Dresden, which is beautifully located along the Elbe valley. Experience in Magdeburg the famous Cathedral and the Monastery. You arrive in the Florence of the Elbe, Dresden, which is beautifully located along the Elbe valley. Magdeburg offers lots of rambling parkways where you can relax. Experience also the famous Cathedral and the Monastery. OK Cycle & Adventure Tours Inc. - 666 Kirkwood Ave - Suite B102 – Ottawa, Ontario Canada K1Z 5X9 www.okcycletours.com Toll Free 1-888-621-6818 Local 613-702-5350 Itinerary Day to Day Day 1: Arrival to Dresden You arrive in the “Florence of the Elbe” Dresden, which is beautifully located along the Elbe valley. Whether the famous Zwinger, the Semper Opera or the Court Church – a tour of the former royal residence by bicycle is worth it. Day 2: Dresden – Meissen 30 km From far away you can already see the landmark of the city of Meissen: the impressive castle hill with the cathedral and Albrechtsburg castle. A visit to the world-famous Meissen porcelain factory is also a must. Enjoy a good wine in the evening as you are in the heart of one of the smallest yet most distinguished winegrowing regions of Germany. Day 3: Meissen – Riesa or Strehla 28 km or 36 km Today’s tour will take you along the picturesque wine villages located along the Elbe River. Next stop will be Riesa, the city of sports or Strehla with an enchanting rural atmosphere.
    [Show full text]
  • How to Handle the Covid-19-Pandemic in Saxony-Anhalt and Magdeburg at the Moment There Are a Many New Infections with the Coronavirus Every Day in Magdeburg
    How to handle the Covid-19-pandemic in Saxony-Anhalt and Magdeburg At the moment there are a many new infections with the Coronavirus every day in Magdeburg. It is important to prevent the virus from spreading fast in order to keep schools and day care/ kindergarten operating and maintain a functional health system. Please take care of yourself and help also to protect others. Therefore reduce the number of private contacts only to essential meetings and try to avoid visits with family and friends. What should I do, if I feel sick or had close contact to somebody, who was tested positivly? Typical symptoms of COVID-19: cough, elevated temperature, fever, shortness of breath, loss of taste or smell, soare throat, headache and muscle aches, or fatigue. If you notice any of these symptoms, stay at home! - do not meet other people, don’t go to work or school - call your doctor or the local public health department (hotline : 0391/ 540 2000) and follow the instructions. - inform your employer and/or the children’s day-care/school - if you notice typical symptoms of COVID-19, you can get tested at Fieberambulanz. - If you show no symptoms of COVID-19, but had contact to an infected person, you will be tested towards the end of quarantine. - Infected people and those, who had contact to infected people stay under quarantine for 14 days (counted from either the positve test result or the day of contact). - A negative test result does not end quarantine. Realisation of Corona test and results: - The test can be realized in Fieberambulanz, Brandenburger Straße 8, 39104 Magdeburg.
    [Show full text]
  • Hamburg - Magdeburg (8 Tage)
    Hamburg - Magdeburg (8 Tage) Beschreibung: Der Elberadweg gehört zu den reizvollsten und abwechslungsreichsten Radwanderrouten Europas. Nehmen Sie sich Zeit, all die landschaftlichen, historischen und kulturellen Orte zu bestaunen! Sie beginnen Ihre Tour in der Hansestadt Hamburg mit ihren zahlreichen Sehenswürdigkeiten und kulturellen Angeboten. Ihre Fahrt führt Sie durch die herrliche norddeutsche Landschaft, die vom Segen und Fluch des Elbwassers geprägt ist. Der mächtige Fluss durchzieht in seinem freien Lauf idyllische Fachwerkdörfer und riesige Obstplantagen. Durch das Biosphärenreservat „Flusslandschaft Elbe“ und die malerische Kaiserstadt Tangermünde führt Sie Ihr Weg bis in die Domstadt Magdeburg. Auch hier lohnt ein längeres Verweilen, denn die Lieblingsresidenz Kaiser Otto I. blickt auf eine 1200-jährige Geschichte zurück. Das flache Terrain ermöglicht es auch dem ungeübten Radler, überall problemlos größere Etappen zu bewältigen. Klicken Sie auf das Bild rechts für weitere Impressionen! Termine: Reisebeginn täglich möglich 01.04. - 31.10.2021 buchbarer Zeitraum: 01.04.2021 - 31.10.2021 Streckenlänge: 353 km Route: Tag 1: Individuelle Anreise nach Hamburg Individuelle Anreise nach Hamburg. Haben Sie Lust abends noch eines der zahlreichen Musicaltheater zu besuchen? Gern sind wir Ihnen bei der Organisation behilflich. Tag 2: Hamburg - Lauenburg (ca. 55 km) Heute beginnt Ihre Radtour Richtung Süden. Erholsam für Auge und Seele sind die stillen Elbauen und eine Wonne für jeden Naturliebhaber. Ihr Etappenziel Lauenburg hat eine malerische Altstadt mit vielen Fachwerkhäusern. Tag 3: Lauenburg - Hitzacker (ca. 57 km) Wenn Sie am linken Elbufer weiterfahren, passieren Sie Bleckede, ein Städtchen am historischen Elbübergang (Fähre) an der „Storchenstraße“. In Hitzacker säumen schmucke Fachwerkhäuser die Ufer des Stromes. Die pittoreske Altstadtinsel mit Fachwerkhäusern und norddeutscher Backsteinarchitektur prägen das Städtchen.
    [Show full text]
  • Smart Cities Final Report
    Smart cities Ranking of European medium-sized cities Research Institute for Centre of Regional Department of Housing, Urban and Science (SRF) Geography Mobility Studies (OTB) Vienna University of University of Delft University of Technology Ljubljana Technology Final report, October 2007 Smart cities – Ranking of European medium-sized cities General notes This report represents the final report of a research project sponsored by Asset One Immo- bilienentwicklungs AG, Kaiser- feldgasse 2, 8010 Graz. The project was elaborated from April to October 2007. This report was edited by the Centre of Regional Science (SRF), Vienna University of Technology in October 2007. Contact: Rudolf Giffinger [email protected] www.srf.tuwien.ac.at Project team The research was carried out in collaborative work of persons from the Centre of Regional Science at the Vienna University of Technology (lead partner), the Department of Geography at University of Ljubljana and the OTB Research Institute for Housing, Urban and Mobility Studies at the Delft University of Technology. Rudolf Giffinger, Vienna UT Christian Fertner, Vienna UT Hans Kramar, Vienna UT Robert Kalasek, Vienna UT Nataša Pichler-Milanović, University of Ljubljana Evert Meijers, Delft UT Moreover thanks to Markus Petzl, Andreas Kleboth, Ernst Giselbrecht for participating contextually at the Kick-Off workshops. Project homepage www.smart-cities.eu © Centre of Regional Science, Vienna UT, October 2007 1 Smart cities – Ranking of European medium-sized cities 2 Smart cities – Ranking of European medium-sized cities Content 1 Background 5 1.1 Aim of the project 5 1.2 The role of city-rankings in regional competition 6 2 Objective 10 2.1 Defining smart city 10 2.2 Operationalizing smart city 11 3 Methodology 13 3.1 Selecting cities 13 3.2 Identifying indicators and data sources 14 3.3 Standardizing and aggregating data 14 4 Results and dissemination 15 4.1 Performance of 70 cities 15 4.2 City profiles 17 4.3 Dissemination 18 4.4 Outlook 18 5 Annex 21 Figures Fig.
    [Show full text]