1 Steiner Minimal Trees

Copy Link

Steiner Minimal Trees^∗

Bang Ye Wu
Kun-Mao Chao

1 Steiner Minimal Trees

⊂
••

−−
−

11
22

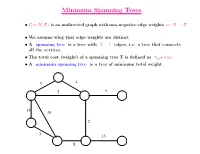
1.1 Approximation by MST

⊂
⊂

Problem Instance Goal

⊂
⊂

^∗An excerpt from the book “Spanning Trees and Optimization Problems,” by Bang Ye Wu and Kun-Mao Chao
(2004), Chapman & Hall/CRC Press, USA.

Exact Cover by 3-Sets
MST-Steiner

⊂
← ∅
∈

v₁
v₂
v₁
v₂

88
4

u₃

u₁

6
5

u₄

u₂

1
4
6
9

5
8
9

v₃
v₃

v₄
v₅

v₄v₅

8
(a)
(b)

v₁
v₂
v₁

4
2

u₁

7
6

u₂

1
5

v₃v₄

v₄
v₅

v₁
v₂

v₁
v₂

u₁u₁

u₂

3
3

v₃v₃v₅v₄v₄

(e)
(f)

MST-Steiner

{ | ≤ ≤ }
≤
≤

∈

21
32

≤

...

1
1
1
2

1
2
1

2
2
2
2

(a)

−
−

| || |

MST-Steiner

| || |

Bibliographic Notes and Further Reading

√
√

References

Recommended publications

‣ Dijkstra's Algorithm ‣ Minimum Spanning Trees ‣ Prim, Kruskal, Boruvka ‣ Single-Link Clustering ‣ Min-Cost Arborescences

4. GREEDY ALGORITHMS II ‣ Dijkstra's algorithm ‣ minimum spanning trees ‣ Prim, Kruskal, Boruvka ‣ single-link clustering ‣ min-cost arborescences Lecture slides by Kevin Wayne Copyright © 2005 Pearson-Addison Wesley http://www.cs.princeton.edu/~wayne/kleinberg-tardos Last updated on Feb 18, 2013 6:08 AM 4. GREEDY ALGORITHMS II ‣ Dijkstra's algorithm ‣ minimum spanning trees ‣ Prim, Kruskal, Boruvka ‣ single-link clustering ‣ min-cost arborescences SECTION 4.4 Shortest-paths problem Problem. Given a digraph G = (V, E), edge weights ℓe ≥ 0, source s ∈ V, and destination t ∈ V, find the shortest directed path from s to t. 1 15 3 5 4 12 source s 0 3 8 7 7 2 9 9 6 1 11 5 5 4 13 4 20 6 destination t length of path = 9 + 4 + 1 + 11 = 25 3 Car navigation 4 Shortest path applications ・PERT/CPM. ・Map routing. ・Seam carving. ・Robot navigation. ・Texture mapping. ・Typesetting in LaTeX. ・Urban traffic planning. ・Telemarketer operator scheduling. ・Routing of telecommunications messages. ・Network routing protocols (OSPF, BGP, RIP). ・Optimal truck routing through given traffic congestion pattern. Reference: Network Flows: Theory, Algorithms, and Applications, R. K. Ahuja, T. L. Magnanti, and J. B. Orlin, Prentice Hall, 1993. 5 Dijkstra's algorithm Greedy approach. Maintain a set of explored nodes S for which algorithm has determined the shortest path distance d(u) from s to u. ・Initialize S = { s }, d(s) = 0. ・Repeatedly choose unexplored node v which minimizes shortest path to some node u in explored part, followed by a single edge (u, v) ℓe v d(u) u S s 6 Dijkstra's algorithm Greedy approach.
Converting MST to TSP Path by Branch Elimination

applied sciences Article Converting MST to TSP Path by Branch Elimination Pasi Fränti 1,2,* , Teemu Nenonen 1 and Mingchuan Yuan 2 1 School of Computing, University of Eastern Finland, 80101 Joensuu, Finland; [email protected] 2 School of Big Data & Internet, Shenzhen Technology University, Shenzhen 518118, China; [email protected] * Correspondence: [email protected].fi Abstract: Travelling salesman problem (TSP) has been widely studied for the classical closed loop variant but less attention has been paid to the open loop variant. Open loop solution has property of being also a spanning tree, although not necessarily the minimum spanning tree (MST). In this paper, we present a simple branch elimination algorithm that removes the branches from MST by cutting one link and then reconnecting the resulting subtrees via selected leaf nodes. The number of iterations equals to the number of branches (b) in the MST. Typically, b << n where n is the number of nodes. With O-Mopsi and Dots datasets, the algorithm reaches gap of 1.69% and 0.61 %, respectively. The algorithm is suitable especially for educational purposes by showing the connection between MST and TSP, but it can also serve as a quick approximation for more complex metaheuristics whose efficiency relies on quality of the initial solution. Keywords: traveling salesman problem; minimum spanning tree; open-loop TSP; Christofides 1. Introduction The classical closed loop variant of travelling salesman problem (TSP) visits all the nodes and then returns to the start node by minimizing the length of the tour. Open loop TSP is slightly different variant, which skips the return to the start node.
CSE 421 Algorithms Warmup Dijkstra's Algorithm

Single Source Shortest Path Problem • Given a graph and a start vertex s – Determine distance of every vertex from s CSE 421 – Identify shortest paths to each vertex Algorithms • Express concisely as a “shortest paths tree” • Each vertex has a pointer to a predecessor on Richard Anderson shortest path 1 u u Dijkstra’s algorithm 1 2 3 5 s x s x 3 4 3 v v Construct Shortest Path Tree Warmup from s • If P is a shortest path from s to v, and if t is 2 d d on the path P, the segment from s to t is a a 1 5 a 4 4 shortest path between s and t 4 e e -3 c s c v -2 s t 3 3 2 s 6 g g b b •WHY? 7 3 f f Assume all edges have non-negative cost Simulate Dijkstra’s algorithm Dijkstra’s Algorithm (strarting from s) on the graph S = {}; d[s] = 0; d[v] = infinity for v != s Round Vertex sabcd While S != V Added Choose v in V-S with minimum d[v] 1 a c 1 Add v to S 1 3 2 For each w in the neighborhood of v 2 s 4 1 d[w] = min(d[w], d[v] + c(v, w)) 4 6 3 4 1 3 y b d 4 1 3 1 u 0 1 1 4 5 s x 2 2 2 2 v 2 3 z 5 Dijkstra’s Algorithm as a greedy Correctness Proof algorithm • Elements committed to the solution by • Elements in S have the correct label order of minimum distance • Key to proof: when v is added to S, it has the correct distance label.
Minimum Spanning Trees Announcements

Lecture 15 Minimum Spanning Trees Announcements • HW5 due Friday • HW6 released Friday Last time • Greedy algorithms • Make a series of choices. • Choose this activity, then that one, .. • Never backtrack. • Show that, at each step, your choice does not rule out success. • At every step, there exists an optimal solution consistent with the choices we’ve made so far. • At the end of the day: • you’ve built only one solution, • never having ruled out success, • so your solution must be correct. Today • Greedy algorithms for Minimum Spanning Tree. • Agenda: 1. What is a Minimum Spanning Tree? 2. Short break to introduce some graph theory tools 3. Prim’s algorithm 4. Kruskal’s algorithm Minimum Spanning Tree Say we have an undirected weighted graph 8 7 B C D 4 9 2 11 4 A I 14 E 7 6 8 10 1 2 A tree is a H G F connected graph with no cycles! A spanning tree is a tree that connects all of the vertices. Minimum Spanning Tree Say we have an undirected weighted graph The cost of a This is a spanning tree is 8 7 spanning tree. the sum of the B C D weights on the edges. 4 9 2 11 4 A I 14 E 7 6 8 10 A tree is a This tree 1 2 H G F connected graph has cost 67 with no cycles! A spanning tree is a tree that connects all of the vertices. Minimum Spanning Tree Say we have an undirected weighted graph This is also a 8 7 spanning tree.
Minimum Perfect Bipartite Matchings and Spanning Trees Under Categorization

View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Elsevier - Publisher Connector Discrete Applied Mathematics 39 (1992) 147- 153 147 North-Holland Minimum perfect bipartite matchings and spanning trees under categorization Michael B. Richey Operations Research & Applied Statistics Department, George Mason University, Fairfax, VA 22030, USA Abraham P. Punnen Mathematics Department, Indian Institute of Technology. Kanpur-208 016, India Received 2 February 1989 Revised 1 May 1990 Abstract Richey, M.B. and A.P. Punnen, Minimum perfect bipartite mats-Yngs and spanning trees under catego- rization, Discrete Applied Mathematics 39 (1992) 147-153. Network optimization problems under categorization arise when the edge set is partitioned into several sets and the objective function is optimized over each set in one sense, then among the sets in some other sense. Here we find that unlike some other problems under categorization, the minimum perfect bipar- tite matching and minimum spanning tree problems (under categorization) are NP-complete, even on bipartite outerplanar graphs. However for one objective function both problems can be solved in polynomial time on arbitrary graphs if the number of sets is fixed. 1. Introduction In operations research and in graph-theoretic optimization, two types of objective functions have dominated the attention of researchers, namely optimization of the weighted sum of the variables and optimization of the most extreme value of the variables. Recently the following type of (minimization) objective function has appeared in the literature [1,6,7,14]: divide the variables into categories, find the Correspondence to: Professor M.B. Richey, Operations Research & Applied Statistics Department, George Mason University, Fairfax, VA 22030, USA.
NP-Hard Problems [Sp’15]

Algorithms Lecture 30: NP-Hard Problems [Sp’15] [I]n his short and broken treatise he provides an eternal example—not of laws, or even of method, for there is no method except to be very intelligent, but of intelligence itself swiftly operating the analysis of sensation to the point of principle and deﬁnition. — T. S. Eliot on Aristotle, “The Perfect Critic”, The Sacred Wood (1921) The nice thing about standards is that you have so many to choose from; furthermore, if you do not like any of them, you can just wait for next year’s model. — Andrew S. Tannenbaum, Computer Networks (1981) Also attributed to Grace Murray Hopper and others If a problem has no solution, it may not be a problem, but a fact — not to be solved, but to be coped with over time. — Shimon Peres, as quoted by David Rumsfeld, Rumsfeld’s Rules (2001) 30 NP-Hard Problems 30.1 A Game You Can’t Win A salesman in a red suit who looks suspiciously like Tom Waits presents you with a black steel box with n binary switches on the front and a light bulb on the top. The salesman tells you that the state of the light bulb is controlled by a complex boolean circuit—a collection of And, Or, and Not gates connected by wires, with one input wire for each switch and a single output wire for the light bulb. He then asks you the following question: Is there a way to set the switches so that the light bulb turns on? If you can answer this question correctly, he will give you the box and a million billion trillion dollars; if you answer incorrectly, or if you die without answering at all, he will take your soul.
Lecture Notes on “Analysis of Algorithms”: Directed Minimum Spanning Trees

Lecture notes on \Analysis of Algorithms": Directed Minimum Spanning Trees Lecturer: Uri Zwick ∗ April 22, 2013 Abstract We describe an efficient implementation of Edmonds' algorithm for finding minimum directed spanning trees in directed graphs. 1 Minimum Directed Spanning Trees Let G = (V; E; w) be a weighted directed graph, where w : E ! R is a cost (or weight) function defined on its edges. Let r 2 V . A directed spanning tree (DST) of G rooted at r, is a subgraph T of G such that the undirected version of T is a tree and T contains a directed path from r to any other vertex in V . The cost w(T ) of a directed spanning tree T is the sum of the costs of its edges, P i.e., w(T ) = e2T w(e). A minimum directed spanning tree (MDST) rooted at r is a directed spanning tree rooted at r of minimum cost. A directed graph contains a directed spanning tree rooted at r if and only if all vertices in G are reachable from r. This condition can be easily tested in linear time. The proof of the following lemma is trivial as is left as an exercise. Lemma 1.1 The following conditions are equivalent: (i) T is a directed spanning tree of G rooted at r. (ii) The indegree of r in T is 0, the indegree of every other vertex of G in T is 1, and T is acyclic, i.e., contains no directed cycles. (iii) The indegree of r in T is 0, the indegree of every other vertex of G in T is 1, and there are directed paths in T from r to all other vertices.
Lecture 8: the Traveling Salesman Problem

TU Eindhoven Advanced Algorithms (2IL45) — Course Notes Lecture 8: The Traveling Salesman Problem Let G = (V, E) be an undirected graph. A Hamiltonian cycle of G is a cycle that visits every vertex v ∈ V exactly once. Instead of Hamiltonian cycle, we sometimes also use the term tour. Not every graph has a Hamiltonian cycle: if the graph is a single path, for example, then obviously it does not have a Hamiltonian cycle. The problem Hamiltonian Cycle is to decide for a given graph graph G whether it has a Hamiltonian cycle. Hamiltonian Cycle is NP-complete. Now suppose that G is a complete graph—that is, G has an edge between every pair of vertices—where each edge e ∈ E has a non-negative length. It is easy to see that because G is complete it must have a Hamiltonian cycle. Since the edges now have lengths, however, some Hamiltonian cycles may be shorter than others. This leads to the traveling salesman problem, or TSP for short: given a complete graph G = (V, E), where each edge e ∈ E has a length, ﬁnd a minimum-length tour (Hamiltonian cycle) of G. (The length of a tour is deﬁned as the sum of the lengths of the edges in the tour.) TSP is NP-hard. We are therefore interested in approximation algorithms. Unfortunately, even this is too much to ask. Theorem 8.1 There is no value c for which there exists a polynomial-time c-approximation algorithm for TSP, unless P=NP. Proof. As noted above, Hamiltonian Cycle is NP-complete, so there is no polynomial-time algorithm for the problem unless P=NP.
‣ Dijkstra′S Algorithm ‣ Minimum Spanning Trees ‣ Prim, Kruskal, Boruvka ‣ Single-Link Clustering ‣ Min-Cost Arborescences

4. GREEDY ALGORITHMS II ‣ Dijkstra′s algorithm ‣ minimum spanning trees ‣ Prim, Kruskal, Boruvka ‣ single-link clustering ‣ min-cost arborescences Lecture slides by Kevin Wayne Copyright © 2005 Pearson-Addison Wesley http://www.cs.princeton.edu/~wayne/kleinberg-tardos Last updated on 2/25/20 4:16 PM 4. GREEDY ALGORITHMS II ‣ Dijkstra′s algorithm ‣ minimum spanning trees ‣ Prim, Kruskal, Boruvka ‣ single-link clustering ‣ min-cost arborescences SECTION 4.4 Single-pair shortest path problem Problem. Given a digraph G = (V, E), edge lengths ℓe ≥ 0, source s ∈ V, and destination t ∈ V, find a shortest directed path from s to t. 1 15 3 5 4 12 source s 0 3 8 7 7 2 9 9 6 1 11 5 5 4 13 4 20 6 destination t length of path = 9 + 4 + 1 + 11 = 25 3 Single-source shortest paths problem Problem. Given a digraph G = (V, E), edge lengths ℓe ≥ 0, source s ∈ V, find a shortest directed path from s to every node. 1 15 3 5 4 12 source s 0 3 8 7 7 2 9 9 6 1 11 5 5 4 13 4 20 6 shortest-paths tree 4 Shortest paths: quiz 1 Suppose that you change the length of every edge of G as follows. For which is every shortest path in G a shortest path in G′? A. Add 17. B. Multiply by 17. C. Either A or B. D. Neither A nor B. 24 —7 s —1 —2 3— t 18 19 20 5 Shortest paths: quiz 2 Which variant in car GPS? A.
$Arxiv:1710.09672V1 [Math.CO] 26 Oct 2017 Minimum Spanning Tree (MST)$

Arxiv:1710.09672V1 [Math.CO] 26 Oct 2017 Minimum Spanning Tree (MST)

1-SKELETONS OF THE SPANNING TREE PROBLEMS WITH ADDITIONAL CONSTRAINTS VLADIMIR BONDARENKO, ANDREI NIKOLAEV, DZHAMBOLET SHOVGENOV Abstract. We consider the polyhedral properties of two spanning tree problems with addi- tional constraints. In the first problem, it is required to find a tree with a minimum sum of edge weights among all spanning trees with the number of leaves less or equal a given value. In the second problem, an additional constraint is the assumption that the degree of all vertices of the spanning tree does not exceed a given value. The decision versions of both problems are NP-complete. We consider the polytopes of these problems and their 1-skeletons. We prove that in both cases it is a NP-complete problem to determine whether the vertices of 1-skeleton are adjacent. Although it is possible to obtain a superpolynomial lower bounds on the clique numbers of these graphs. These values characterize the time complexity in a broad class of algorithms based on linear comparisons. The results indicate a fundamental difference in combinatorial and geometric properties between the considered problems and the classical minimum spanning tree problem. 1. Introduction A significant number of works related to the computational complexity of combinatorial prob- lems is aimed at the study of geometric objects associated with problems. Usually such objects are the polytopes of the problems and their 1-skeletons. In particular, the clique number of the 1-skeleton (the size of the maximum clique) of the problem serves as a lower bound on compu- tational complexity in a broad class of algorithms based on linear comparisons.
Combinatorial Characterisations of Graphical Computational Search

Combinatorial Characterisations of accessible Graphical Computational Search Problems: P= 6 NP. Kayibi Koko-Kalambay School of Mathematics. Department of Sciences University of Bristol Abstract Let G be a connected graph with edge-set E and vertex-set V . Given an input X, where X is the edge-set or the vertex-set of the graph G, a graphical computational search problem associated with a predicate γ con- sists of finding a solution Y , where Y ⊆ X, and Y satisfies the condition γ. We denote such a problem as Π(X; γ), and we let Π^ to denote the decision problem associated with Π(X; γ). A sub-solution of Π(X; γ) is a subset Y 0 that is a solution of the problem Π(X0; γ), where X0 ⊂ X, and X0 is the edge-set or the vertex-set of the contraction-minor G=A, where A ⊆ E. To each search problem Π(X; γ), we associate the set system (X; I), where I denotes the set of all the solutions and sub-solutions of Π(X; γ). The predicate γ is an accessible predicate if, given Y 6= ;, Y satisfies γ in X implies that there is an element y 2 Y such that Y n y satisfies γ in X0. If γ is an accessible property, we then show in Theorem 1 that a decision problem Π^ is in P if and only if, for all input X, the set system (X; I) satisfies Axioms M2', where M2', called the Augmentability Axiom, is an extension of both the Exchange Axiom and the Accessibility Axiom of a greedoid.
Minimum Spanning Trees

Minimum Spanning Trees • G = (V; E) is an undirected graph with non-negative edge weights w : E ! Z+ • We assume wlog that edge weights are distinct • A spanning tree is a tree with V − 1 edges, i.e. a tree that connects all the vertices. P • The total cost (weight) of a spanning tree T is deﬁned as e2T w(e) • A minimum spanning tree is a tree of minimum total weight. 6 4 5 9 14 10 2 3 15 8 Minimum Spanning Trees • G = (V; E) is an undirected graph with non-negative edge weights w : E ! Z+ • We assume wlog that edge weights are distinct • A spanning tree is a tree with V − 1 edges, i.e. a tree that connects all the vertices. P • The total cost (weight) of a spanning tree T is deﬁned as e2T w(e) • A minimum spanning tree is a tree of minimum total weight. 6 4 5 9 14 10 2 3 15 8 Cuts • A cut in a graph is a partition of the vertices into two sets S and T . • An edge (u; v) with u 2 S and v 2 T is said to cross the cut. 6 4 5 9 14 10 2 3 15 8 Cuts • A cut in a graph is a partition of the vertices into two sets S and T . • An edge (u; v) with u 2 S and v 2 T is said to cross the cut. 6 4 5 9 14 10 2 3 15 8 Cuts • A cut in a graph is a partition of the vertices into two sets S and T .