DOCSLIB.ORG

Converting MST to TSP Path by Branch Elimination

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Converting MST to TSP Path by Branch Elimination applied sciences Article Converting MST to TSP Path by Branch Elimination Pasi Fränti 1,2,* , Teemu Nenonen 1 and Mingchuan Yuan 2 1 School of Computing, University of Eastern Finland, 80101 Joensuu, Finland; [email protected] 2 School of Big Data & Internet, Shenzhen Technology University, Shenzhen 518118, China; [email protected] * Correspondence: [email protected].fi Abstract: Travelling salesman problem (TSP) has been widely studied for the classical closed loop variant but less attention has been paid to the open loop variant. Open loop solution has property of being also a spanning tree, although not necessarily the minimum spanning tree (MST). In this paper, we present a simple branch elimination algorithm that removes the branches from MST by cutting one link and then reconnecting the resulting subtrees via selected leaf nodes. The number of iterations equals to the number of branches (b) in the MST. Typically, b << n where n is the number of nodes. With O-Mopsi and Dots datasets, the algorithm reaches gap of 1.69% and 0.61 %, respectively. The algorithm is suitable especially for educational purposes by showing the connection between MST and TSP, but it can also serve as a quick approximation for more complex metaheuristics whose efficiency relies on quality of the initial solution. Keywords: traveling salesman problem; minimum spanning tree; open-loop TSP; Christofides 1. Introduction The classical closed loop variant of travelling salesman problem (TSP) visits all the nodes and then returns to the start node by minimizing the length of the tour. Open loop TSP is slightly different variant, which skips the return to the start node. They are both NP-hard problems [1], which means that finding optimal solution fast can be done only for very Citation: Fränti, P.; Nenonen, T.; small size inputs. Yuan, M. Converting MST to TSP The open loop variant appears in mobile-based orienteering game called O-Mopsi Path by Branch Elimination. Appl. Sci. (http://cs.uef.fi/o-mopsi/) where the goal is to find a set of real-world targets with the 2021, 11, 177. https://dx.doi.org/ help of smartphone navigation [2]. This includes three challenges: (1) Deciding the order 10.3390/11010177 of visiting the targets, (2) navigating to the next target, and (3) physical movement. Unlike in classical orienteering where the order of visiting the targets is fixed, O-Mopsi players Received: 23 November 2020 optimize the order while playing. Finding the optimal order is not necessary but desirable Accepted: 24 December 2020 Published: 27 December 2020 if one wants to minimize the tour length. However, the task is quite challenging for humans even for short problem instances. In [2], only 14% of the players managed to solve the best Publisher’s Note: MDPI stays neu- order among those who completed the tour. Most players did not even realize they were tral with regard to jurisdictional claims dealing with TSP problem. in published maps and institutional Minimum spanning tree (MST) and TSP are closely related algorithmic problems. In spe- affiliations. cific, open loop TSP solution is also a spanning tree but not necessarily the minimum spanning tree; see Figure1. The solutions have the same number of links ( n − 1) and they both minimize the total weight of the selected links. The difference is that TSP does not have any branches. This connection is interesting for two reasons. First, finding optimal Copyright: © 2020 by the authors. Li- solution for TSP requires exponential time while optimal solution for MST can be found in censee MDPI, Basel, Switzerland. This polynomial time using greedy algorithms like Prim and Kruskal, with time complexity very article is an open access article distributed close to O(n2) with appropriate data structure. under the terms and conditions of the The connection between the two problems have inspired researchers to develop heuris- Creative Commons Attribution (CC BY) tic algorithms for the TSP by utilizing the minimum spanning tree. Classical schoolbook license (https://creativecommons.org/ algorithm is Christofides [3,4], which first creates an MST. More links are then added so licenses/by/4.0/). Appl. Sci. 2021, 11, 177. https://dx.doi.org/10.3390/app11010177 https://www.mdpi.com/journal/applsci Appl. Sci. 2021, 11, 177 2 of 17 that the Euler tour can be constructed. Travelling salesman tour is obtained from the Euler tour by removing nodes that are visited repeatedly. This algorithm is often used as classroom example because it provides upper limit how far the solution can be from the Appl. Sci. 2021, 11, x FOR PEER REVIEW 2 of 17 optimal solution in the worst case. Even if the upper limit, 50%, is rather high for real life applications, it serves as an example of the principle of approximation algorithms. Figure 1. MinimumFigure 1. spanningMinimum tree spanning(MST) (left) tree and (MST) open loop (left) travel andling open salesman looptravelling problem (TSP) salesman solutions problem (right) for (TSP) the same problemsolutions instance. (right) The branching for the same nodes problem are shown instance. by blue, and The the branching links that nodesare different are shown in the two by blue, solutions and have the thicker blacklinks line. that In addition are different to the inbran theches, two there solutions are only have two thicker other places black (red line. circles) In addition where tothe the two branches, solutions differ. there Among all links, 29/37 = 78% are the same in both solutions. are only two other places (red circles) where the two solutions differ. Among all links, 29/37 = 78% are the same in bothThe solutions. connection between the two problems have inspired researchers to develop heu- ristic algorithms for the TSP by utilizing the minimum spanning tree. Classical schoolbook MST hasalgorithm also been is usedChristofides to estimate [3,4], which lower first limit creates forthe an MST. optimal More TSP links solution are then in added [5], so and to estimatethat the the difficultyEuler tour ofcan a be TSP constructed. instance Travel by countingling salesman the number tour is obtained of branches from the [6]. Euler Prim’s and Kruskal’stour by removing algorithms nodes can that also are been visited modified repeatedly. to obtainThis algorithm sub-optimal is often solutions used as class- for TSP. Classroom of insertion example algorithms because itwere provides studied upper in limit [7]. Theyhow far iteratively the solution add can new be nodesfrom the to opti- the current path.mal Thesolution variant in the that worst adds case. a new Even node if the to eitherupper endlimit, of 50%, the existingis rather pathhigh canfor bereal life seen as modificationapplications, of the it Prim’sserves as algorithm an example where of the additions principle areof approximation allowed only algorithms to the ends. of the path. Similarly,MST has algorithm also been called used Kruskal-TSPto estimate lower[8] modifieslimit for the Kruskal’s optimal algorithmTSP solution so in [5], that it allowsand to merge to estimate two spanningthe difficulty trees of (pathsa TSP instan in casece ofby TSP)counting only the by number their end of points.branches [6]. In this paper,Prim’s we and introduce Kruskal’s aalgorithms more sophisticated can also been approach modified to obtain utilize sub-optimal the minimum solutions spanning treefor to TSP. obtain Class solution of insertion for travellingalgorithms were salesman studied problem. in [7]. They The iteratively algorithm, add called new nodes to the current path. The variant that adds a new node to either end of the existing path MST-to-TSP, creates a minimum spanning tree using any algorithm such as Prim or Kruskal. can be seen as modification of the Prim’s algorithm where additions are allowed only to However, instead of adding redundant links like Chirstofides, we detect branching nodes the ends of the path. Similarly, algorithm called Kruskal-TSP [8] modifies Kruskal’s algo- and eliminaterithm them so bythat a it series allows of tolink merge swaps, two spanning see Figure trees2. (pathsBranching in case nodeof TSP)is aonly node by their that connectsend more points. than two other nodes in the tree [6]. We introduce two strategies. First, a simple greedyIn thisvariant paper, removeswe introduce the a longest more soph of allisticated links approach connecting to utilize to any the of minimum the branching nodes.spanning The tree resulting to obtain sub-trees solution are for thentravelling reconnected salesman by problem. selecting The the algorithm, shortest called link betweenMST-to-TSP leaf nodes., Thecreates second a minimum strategy, spanningall-pairs tree, considers using any allalgorithm possible such removal as Prim and or Krus- reconnection possibilitieskal. However, and instead selects of adding the best redundant pair. links like Chirstofides, we detect branching We test thenodes algorithm and eliminate with them two datasetsby a series consisting of link swaps, of open see Figure loop 2. problem Branching instances node is a node with known groundthat connects truth: more O-Mopsi than two [2] other and Dotsnodes [ 9in]. the Experiments tree [6]. We introduce show that two the strategies. all-pairs First, variant providea simple average greedy gaps variant of 1.69% removes (O-Mopsi) the longest and of 0.61% all links (Dots). connecting These areto any clearly of the better branching than those ofnodes. the existing The resulting MST-based sub-trees variants are then including reconnected Christofides by selecting (12.77% the shortest and 9.10%),link between leaf nodes. The second strategy, all-pairs, considers all possible removal and reconnection Prim-TSP (6.57% and 3.84%), and Kruskal-TSP (4.87% and 2.66%). Although sub-optimal, possibilities and selects the best pair. the algorithm is useful to provide reasonable estimate for the TSP solution.
Load more

Recommended publications
  • 1 Steiner Minimal Trees
    Steiner Minimal Trees¤ Bang Ye Wu Kun-Mao Chao 1 Steiner Minimal Trees While a spanning tree spans all vertices of a given graph, a Steiner tree spans a given subset of vertices. In the Steiner minimal tree problem, the vertices are divided into two parts: terminals and nonterminal vertices. The terminals are the given vertices which must be included in the solution. The cost of a Steiner tree is de¯ned as the total edge weight. A Steiner tree may contain some nonterminal vertices to reduce the cost. Let V be a set of vertices. In general, we are given a set L ½ V of terminals and a metric de¯ning the distance between any two vertices in V . The objective is to ¯nd a connected subgraph spanning all the terminals of minimal total cost. Since the distances are all nonnegative in a metric, the solution is a tree structure. Depending on the given metric, two versions of the Steiner tree problem have been studied. ² (Graph) Steiner minimal trees (SMT): In this version, the vertex set and metric is given by a ¯nite graph. ² Euclidean Steiner minimal trees (Euclidean SMT): In this version, V is the entire Euclidean space and thus in¯nite. Usually the metric is given by the Euclidean distance 2 (L -norm). That is, for two points with coordinates (x1; y2) and (x2; y2), the distance is p 2 2 (x1 ¡ x2) + (y1 ¡ y2) : In some applications such as VLSI routing, L1-norm, also known as rectilinear distance, is used, in which the distance is de¯ned as jx1 ¡ x2j + jy1 ¡ y2j: Figure 1 illustrates a Euclidean Steiner minimal tree and a graph Steiner minimal tree.
    [Show full text]
  • ‣ Dijkstra's Algorithm ‣ Minimum Spanning Trees ‣ Prim, Kruskal, Boruvka ‣ Single-Link Clustering ‣ Min-Cost Arborescences
    4. GREEDY ALGORITHMS II ‣ Dijkstra's algorithm ‣ minimum spanning trees ‣ Prim, Kruskal, Boruvka ‣ single-link clustering ‣ min-cost arborescences Lecture slides by Kevin Wayne Copyright © 2005 Pearson-Addison Wesley http://www.cs.princeton.edu/~wayne/kleinberg-tardos Last updated on Feb 18, 2013 6:08 AM 4. GREEDY ALGORITHMS II ‣ Dijkstra's algorithm ‣ minimum spanning trees ‣ Prim, Kruskal, Boruvka ‣ single-link clustering ‣ min-cost arborescences SECTION 4.4 Shortest-paths problem Problem. Given a digraph G = (V, E), edge weights ℓe ≥ 0, source s ∈ V, and destination t ∈ V, find the shortest directed path from s to t. 1 15 3 5 4 12 source s 0 3 8 7 7 2 9 9 6 1 11 5 5 4 13 4 20 6 destination t length of path = 9 + 4 + 1 + 11 = 25 3 Car navigation 4 Shortest path applications ・PERT/CPM. ・Map routing. ・Seam carving. ・Robot navigation. ・Texture mapping. ・Typesetting in LaTeX. ・Urban traffic planning. ・Telemarketer operator scheduling. ・Routing of telecommunications messages. ・Network routing protocols (OSPF, BGP, RIP). ・Optimal truck routing through given traffic congestion pattern. Reference: Network Flows: Theory, Algorithms, and Applications, R. K. Ahuja, T. L. Magnanti, and J. B. Orlin, Prentice Hall, 1993. 5 Dijkstra's algorithm Greedy approach. Maintain a set of explored nodes S for which algorithm has determined the shortest path distance d(u) from s to u. ・Initialize S = { s }, d(s) = 0. ・Repeatedly choose unexplored node v which minimizes shortest path to some node u in explored part, followed by a single edge (u, v) ℓe v d(u) u S s 6 Dijkstra's algorithm Greedy approach.
    [Show full text]
  • CSE 421 Algorithms Warmup Dijkstra's Algorithm
    Single Source Shortest Path Problem • Given a graph and a start vertex s – Determine distance of every vertex from s CSE 421 – Identify shortest paths to each vertex Algorithms • Express concisely as a “shortest paths tree” • Each vertex has a pointer to a predecessor on Richard Anderson shortest path 1 u u Dijkstra’s algorithm 1 2 3 5 s x s x 3 4 3 v v Construct Shortest Path Tree Warmup from s • If P is a shortest path from s to v, and if t is 2 d d on the path P, the segment from s to t is a a 1 5 a 4 4 shortest path between s and t 4 e e -3 c s c v -2 s t 3 3 2 s 6 g g b b •WHY? 7 3 f f Assume all edges have non-negative cost Simulate Dijkstra’s algorithm Dijkstra’s Algorithm (strarting from s) on the graph S = {}; d[s] = 0; d[v] = infinity for v != s Round Vertex sabcd While S != V Added Choose v in V-S with minimum d[v] 1 a c 1 Add v to S 1 3 2 For each w in the neighborhood of v 2 s 4 1 d[w] = min(d[w], d[v] + c(v, w)) 4 6 3 4 1 3 y b d 4 1 3 1 u 0 1 1 4 5 s x 2 2 2 2 v 2 3 z 5 Dijkstra’s Algorithm as a greedy Correctness Proof algorithm • Elements committed to the solution by • Elements in S have the correct label order of minimum distance • Key to proof: when v is added to S, it has the correct distance label.
    [Show full text]
  • Minimum Spanning Trees Announcements
    Lecture 15 Minimum Spanning Trees Announcements • HW5 due Friday • HW6 released Friday Last time • Greedy algorithms • Make a series of choices. • Choose this activity, then that one, .. • Never backtrack. • Show that, at each step, your choice does not rule out success. • At every step, there exists an optimal solution consistent with the choices we’ve made so far. • At the end of the day: • you’ve built only one solution, • never having ruled out success, • so your solution must be correct. Today • Greedy algorithms for Minimum Spanning Tree. • Agenda: 1. What is a Minimum Spanning Tree? 2. Short break to introduce some graph theory tools 3. Prim’s algorithm 4. Kruskal’s algorithm Minimum Spanning Tree Say we have an undirected weighted graph 8 7 B C D 4 9 2 11 4 A I 14 E 7 6 8 10 1 2 A tree is a H G F connected graph with no cycles! A spanning tree is a tree that connects all of the vertices. Minimum Spanning Tree Say we have an undirected weighted graph The cost of a This is a spanning tree is 8 7 spanning tree. the sum of the B C D weights on the edges. 4 9 2 11 4 A I 14 E 7 6 8 10 A tree is a This tree 1 2 H G F connected graph has cost 67 with no cycles! A spanning tree is a tree that connects all of the vertices. Minimum Spanning Tree Say we have an undirected weighted graph This is also a 8 7 spanning tree.
    [Show full text]
  • Minimum Perfect Bipartite Matchings and Spanning Trees Under Categorization
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Elsevier - Publisher Connector Discrete Applied Mathematics 39 (1992) 147- 153 147 North-Holland Minimum perfect bipartite matchings and spanning trees under categorization Michael B. Richey Operations Research & Applied Statistics Department, George Mason University, Fairfax, VA 22030, USA Abraham P. Punnen Mathematics Department, Indian Institute of Technology. Kanpur-208 016, India Received 2 February 1989 Revised 1 May 1990 Abstract Richey, M.B. and A.P. Punnen, Minimum perfect bipartite mats-Yngs and spanning trees under catego- rization, Discrete Applied Mathematics 39 (1992) 147-153. Network optimization problems under categorization arise when the edge set is partitioned into several sets and the objective function is optimized over each set in one sense, then among the sets in some other sense. Here we find that unlike some other problems under categorization, the minimum perfect bipar- tite matching and minimum spanning tree problems (under categorization) are NP-complete, even on bipartite outerplanar graphs. However for one objective function both problems can be solved in polynomial time on arbitrary graphs if the number of sets is fixed. 1. Introduction In operations research and in graph-theoretic optimization, two types of objective functions have dominated the attention of researchers, namely optimization of the weighted sum of the variables and optimization of the most extreme value of the variables. Recently the following type of (minimization) objective function has appeared in the literature [1,6,7,14]: divide the variables into categories, find the Correspondence to: Professor M.B. Richey, Operations Research & Applied Statistics Department, George Mason University, Fairfax, VA 22030, USA.
    [Show full text]
  • NP-Hard Problems [Sp’15]
    Algorithms Lecture 30: NP-Hard Problems [Sp’15] [I]n his short and broken treatise he provides an eternal example—not of laws, or even of method, for there is no method except to be very intelligent, but of intelligence itself swiftly operating the analysis of sensation to the point of principle and definition. — T. S. Eliot on Aristotle, “The Perfect Critic”, The Sacred Wood (1921) The nice thing about standards is that you have so many to choose from; furthermore, if you do not like any of them, you can just wait for next year’s model. — Andrew S. Tannenbaum, Computer Networks (1981) Also attributed to Grace Murray Hopper and others If a problem has no solution, it may not be a problem, but a fact — not to be solved, but to be coped with over time. — Shimon Peres, as quoted by David Rumsfeld, Rumsfeld’s Rules (2001) 30 NP-Hard Problems 30.1 A Game You Can’t Win A salesman in a red suit who looks suspiciously like Tom Waits presents you with a black steel box with n binary switches on the front and a light bulb on the top. The salesman tells you that the state of the light bulb is controlled by a complex boolean circuit—a collection of And, Or, and Not gates connected by wires, with one input wire for each switch and a single output wire for the light bulb. He then asks you the following question: Is there a way to set the switches so that the light bulb turns on? If you can answer this question correctly, he will give you the box and a million billion trillion dollars; if you answer incorrectly, or if you die without answering at all, he will take your soul.
    [Show full text]
  • Lecture Notes on “Analysis of Algorithms”: Directed Minimum Spanning Trees
    Lecture notes on \Analysis of Algorithms": Directed Minimum Spanning Trees Lecturer: Uri Zwick ∗ April 22, 2013 Abstract We describe an efficient implementation of Edmonds' algorithm for finding minimum directed spanning trees in directed graphs. 1 Minimum Directed Spanning Trees Let G = (V; E; w) be a weighted directed graph, where w : E ! R is a cost (or weight) function defined on its edges. Let r 2 V . A directed spanning tree (DST) of G rooted at r, is a subgraph T of G such that the undirected version of T is a tree and T contains a directed path from r to any other vertex in V . The cost w(T ) of a directed spanning tree T is the sum of the costs of its edges, P i.e., w(T ) = e2T w(e). A minimum directed spanning tree (MDST) rooted at r is a directed spanning tree rooted at r of minimum cost. A directed graph contains a directed spanning tree rooted at r if and only if all vertices in G are reachable from r. This condition can be easily tested in linear time. The proof of the following lemma is trivial as is left as an exercise. Lemma 1.1 The following conditions are equivalent: (i) T is a directed spanning tree of G rooted at r. (ii) The indegree of r in T is 0, the indegree of every other vertex of G in T is 1, and T is acyclic, i.e., contains no directed cycles. (iii) The indegree of r in T is 0, the indegree of every other vertex of G in T is 1, and there are directed paths in T from r to all other vertices.
    [Show full text]
  • Lecture 8: the Traveling Salesman Problem
    TU Eindhoven Advanced Algorithms (2IL45) — Course Notes Lecture 8: The Traveling Salesman Problem Let G = (V, E) be an undirected graph. A Hamiltonian cycle of G is a cycle that visits every vertex v ∈ V exactly once. Instead of Hamiltonian cycle, we sometimes also use the term tour. Not every graph has a Hamiltonian cycle: if the graph is a single path, for example, then obviously it does not have a Hamiltonian cycle. The problem Hamiltonian Cycle is to decide for a given graph graph G whether it has a Hamiltonian cycle. Hamiltonian Cycle is NP-complete. Now suppose that G is a complete graph—that is, G has an edge between every pair of vertices—where each edge e ∈ E has a non-negative length. It is easy to see that because G is complete it must have a Hamiltonian cycle. Since the edges now have lengths, however, some Hamiltonian cycles may be shorter than others. This leads to the traveling salesman problem, or TSP for short: given a complete graph G = (V, E), where each edge e ∈ E has a length, find a minimum-length tour (Hamiltonian cycle) of G. (The length of a tour is defined as the sum of the lengths of the edges in the tour.) TSP is NP-hard. We are therefore interested in approximation algorithms. Unfortunately, even this is too much to ask. Theorem 8.1 There is no value c for which there exists a polynomial-time c-approximation algorithm for TSP, unless P=NP. Proof. As noted above, Hamiltonian Cycle is NP-complete, so there is no polynomial-time algorithm for the problem unless P=NP.
    [Show full text]
  • ‣ Dijkstra′S Algorithm ‣ Minimum Spanning Trees ‣ Prim, Kruskal, Boruvka ‣ Single-Link Clustering ‣ Min-Cost Arborescences
    4. GREEDY ALGORITHMS II ‣ Dijkstra′s algorithm ‣ minimum spanning trees ‣ Prim, Kruskal, Boruvka ‣ single-link clustering ‣ min-cost arborescences Lecture slides by Kevin Wayne Copyright © 2005 Pearson-Addison Wesley http://www.cs.princeton.edu/~wayne/kleinberg-tardos Last updated on 2/25/20 4:16 PM 4. GREEDY ALGORITHMS II ‣ Dijkstra′s algorithm ‣ minimum spanning trees ‣ Prim, Kruskal, Boruvka ‣ single-link clustering ‣ min-cost arborescences SECTION 4.4 Single-pair shortest path problem Problem. Given a digraph G = (V, E), edge lengths ℓe ≥ 0, source s ∈ V, and destination t ∈ V, find a shortest directed path from s to t. 1 15 3 5 4 12 source s 0 3 8 7 7 2 9 9 6 1 11 5 5 4 13 4 20 6 destination t length of path = 9 + 4 + 1 + 11 = 25 3 Single-source shortest paths problem Problem. Given a digraph G = (V, E), edge lengths ℓe ≥ 0, source s ∈ V, find a shortest directed path from s to every node. 1 15 3 5 4 12 source s 0 3 8 7 7 2 9 9 6 1 11 5 5 4 13 4 20 6 shortest-paths tree 4 Shortest paths: quiz 1 Suppose that you change the length of every edge of G as follows. For which is every shortest path in G a shortest path in G′? A. Add 17. B. Multiply by 17. C. Either A or B. D. Neither A nor B. 24 —7 s —1 —2 3— t 18 19 20 5 Shortest paths: quiz 2 Which variant in car GPS? A.
    [Show full text]
  • Arxiv:1710.09672V1 [Math.CO] 26 Oct 2017 Minimum Spanning Tree (MST)
    1-SKELETONS OF THE SPANNING TREE PROBLEMS WITH ADDITIONAL CONSTRAINTS VLADIMIR BONDARENKO, ANDREI NIKOLAEV, DZHAMBOLET SHOVGENOV Abstract. We consider the polyhedral properties of two spanning tree problems with addi- tional constraints. In the first problem, it is required to find a tree with a minimum sum of edge weights among all spanning trees with the number of leaves less or equal a given value. In the second problem, an additional constraint is the assumption that the degree of all vertices of the spanning tree does not exceed a given value. The decision versions of both problems are NP-complete. We consider the polytopes of these problems and their 1-skeletons. We prove that in both cases it is a NP-complete problem to determine whether the vertices of 1-skeleton are adjacent. Although it is possible to obtain a superpolynomial lower bounds on the clique numbers of these graphs. These values characterize the time complexity in a broad class of algorithms based on linear comparisons. The results indicate a fundamental difference in combinatorial and geometric properties between the considered problems and the classical minimum spanning tree problem. 1. Introduction A significant number of works related to the computational complexity of combinatorial prob- lems is aimed at the study of geometric objects associated with problems. Usually such objects are the polytopes of the problems and their 1-skeletons. In particular, the clique number of the 1-skeleton (the size of the maximum clique) of the problem serves as a lower bound on compu- tational complexity in a broad class of algorithms based on linear comparisons.
    [Show full text]
  • Combinatorial Characterisations of Graphical Computational Search
    Combinatorial Characterisations of accessible Graphical Computational Search Problems: P= 6 NP. Kayibi Koko-Kalambay School of Mathematics. Department of Sciences University of Bristol Abstract Let G be a connected graph with edge-set E and vertex-set V . Given an input X, where X is the edge-set or the vertex-set of the graph G, a graphical computational search problem associated with a predicate γ con- sists of finding a solution Y , where Y ⊆ X, and Y satisfies the condition γ. We denote such a problem as Π(X; γ), and we let Π^ to denote the decision problem associated with Π(X; γ). A sub-solution of Π(X; γ) is a subset Y 0 that is a solution of the problem Π(X0; γ), where X0 ⊂ X, and X0 is the edge-set or the vertex-set of the contraction-minor G=A, where A ⊆ E. To each search problem Π(X; γ), we associate the set system (X; I), where I denotes the set of all the solutions and sub-solutions of Π(X; γ). The predicate γ is an accessible predicate if, given Y 6= ;, Y satisfies γ in X implies that there is an element y 2 Y such that Y n y satisfies γ in X0. If γ is an accessible property, we then show in Theorem 1 that a decision problem Π^ is in P if and only if, for all input X, the set system (X; I) satisfies Axioms M2', where M2', called the Augmentability Axiom, is an extension of both the Exchange Axiom and the Accessibility Axiom of a greedoid.
    [Show full text]
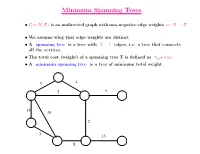
  • Minimum Spanning Trees
    Minimum Spanning Trees • G = (V; E) is an undirected graph with non-negative edge weights w : E ! Z+ • We assume wlog that edge weights are distinct • A spanning tree is a tree with V − 1 edges, i.e. a tree that connects all the vertices. P • The total cost (weight) of a spanning tree T is defined as e2T w(e) • A minimum spanning tree is a tree of minimum total weight. 6 4 5 9 14 10 2 3 15 8 Minimum Spanning Trees • G = (V; E) is an undirected graph with non-negative edge weights w : E ! Z+ • We assume wlog that edge weights are distinct • A spanning tree is a tree with V − 1 edges, i.e. a tree that connects all the vertices. P • The total cost (weight) of a spanning tree T is defined as e2T w(e) • A minimum spanning tree is a tree of minimum total weight. 6 4 5 9 14 10 2 3 15 8 Cuts • A cut in a graph is a partition of the vertices into two sets S and T . • An edge (u; v) with u 2 S and v 2 T is said to cross the cut. 6 4 5 9 14 10 2 3 15 8 Cuts • A cut in a graph is a partition of the vertices into two sets S and T . • An edge (u; v) with u 2 S and v 2 T is said to cross the cut. 6 4 5 9 14 10 2 3 15 8 Cuts • A cut in a graph is a partition of the vertices into two sets S and T .
    [Show full text]