Dependent Sources and Ideal Op Amps
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Chapter 2 Basic Concepts in RF Design
Chapter 2 Basic Concepts in RF Design 1 Sections to be covered • 2.1 General Considerations • 2.2 Effects of Nonlinearity • 2.3 Noise • 2.4 Sensitivity and Dynamic Range • 2.5 Passive Impedance Transformation 2 Chapter Outline Nonlinearity Noise Impedance Harmonic Distortion Transformation Compression Noise Spectrum Intermodulation Device Noise Series-Parallel Noise in Circuits Conversion Matching Networks 3 The Big Picture: Generic RF Transceiver Overall transceiver Signals are upconverted/downconverted at TX/RX, by an oscillator controlled by a Frequency Synthesizer. 4 General Considerations: Units in RF Design Voltage gain: rms value Power gain: These two quantities are equal (in dB) only if the input and output impedance are equal. Example: an amplifier having an input resistance of R0 (e.g., 50 Ω) and driving a load resistance of R0 : 5 where Vout and Vin are rms value. General Considerations: Units in RF Design “dBm” The absolute signal levels are often expressed in dBm (not in watts or volts); Used for power quantities, the unit dBm refers to “dB’s above 1mW”. To express the signal power, Psig, in dBm, we write 6 Example of Units in RF An amplifier senses a sinusoidal signal and delivers a power of 0 dBm to a load resistance of 50 Ω. Determine the peak-to-peak voltage swing across the load. Solution: a sinusoid signal having a peak-to-peak amplitude of Vpp an rms value of Vpp/(2√2), 0dBm is equivalent to 1mW, where RL= 50 Ω thus, 7 Example of Units in RF A GSM receiver senses a narrowband (modulated) signal having a level of -100 dBm. -

The Basics of Power the Background of Some of the Electronics
We Often talk abOut systeMs from a “in front of the (working) screen” or a Rudi van Drunen “software” perspective. Behind all this there is a complex hardware architecture that makes things work. This is your machine: the machine room, the network, and all. Everything has to do with electronics and electrical signals. In this article I will discuss the basics of power the background of some of the electronics, Rudi van Drunen is a senior UNIX systems consul- introducing the basics of power and how tant with Competa IT B.V. in the Netherlands. He to work with it, so that you will be able to also has his own consulting company, Xlexit Tech- nology, doing low-level hardware-oriented jobs. understand the issues and calculations that [email protected] are the basis of delivering the electrical power that makes your system work. There are some basic things that drive the electrons through your machine. I will be explaining Ohm’s law, the power law, and some aspects that will show you how to lay out your power grid. power Law Any piece of equipment connected to a power source will cause a current to flow. The current will then have the device perform its actions (and produce heat). To calculate the current that will be flowing through the machine (or light bulb) we divide the power rating (in watts) by the voltage (in volts) to which the system is connected. An ex- ample here is if you take a 100-watt light bulb and connect this light bulb to the wall power voltage of 115 volts, the resulting current will be 100/115 = 0.87 amperes. -

Automated Problem and Solution Generation Software for Computer-Aided Instruction in Elementary Linear Circuit Analysis
AC 2012-4437: AUTOMATED PROBLEM AND SOLUTION GENERATION SOFTWARE FOR COMPUTER-AIDED INSTRUCTION IN ELEMENTARY LINEAR CIRCUIT ANALYSIS Mr. Charles David Whitlatch, Arizona State University Mr. Qiao Wang, Arizona State University Dr. Brian J. Skromme, Arizona State University Brian Skromme obtained a B.S. degree in electrical engineering with high honors from the University of Wisconsin, Madison and M.S. and Ph.D. degrees in electrical engineering from the University of Illinois, Urbana-Champaign. He was a member of technical staff at Bellcore from 1985-1989 when he joined Ari- zona State University. He is currently professor in the School of Electrical, Computer, and Energy Engi- neering and Assistant Dean in Academic and Student Affairs. He has more than 120 refereed publications in solid state electronics and is active in freshman retention, computer-aided instruction, curriculum, and academic integrity activities, as well as teaching and research. c American Society for Engineering Education, 2012 Automated Problem and Solution Generation Software for Computer-Aided Instruction in Elementary Linear Circuit Analysis Abstract Initial progress is described on the development of a software engine capable of generating and solving textbook-like problems of randomly selected topologies and element values that are suitable for use in courses on elementary linear circuit analysis. The circuit generation algorithms are discussed in detail, including the criteria that define an “acceptable” circuit of the type typically used for this purpose. The operation of the working prototype is illustrated, showing automated problem generation, node and mesh analysis, and combination of series and parallel elements. Various graphical features are available to support student understanding, and an interactive exercise in identifying series and parallel elements is provided. -

9 Op-Amps and Transistors
Notes for course EE1.1 Circuit Analysis 2004-05 TOPIC 9 – OPERATIONAL AMPLIFIER AND TRANSISTOR CIRCUITS . Op-amp basic concepts and sub-circuits . Practical aspects of op-amps; feedback and stability . Nodal analysis of op-amp circuits . Transistor models . Frequency response of op-amp and transistor circuits 1 THE OPERATIONAL AMPLIFIER: BASIC CONCEPTS AND SUB-CIRCUITS 1.1 General The operational amplifier is a universal active element It is cheap and small and easier to use than transistors It usually takes the form of an integrated circuit containing about 50 – 100 transistors; the circuit is designed to approximate an ideal controlled source; for many situations, its characteristics can be considered as ideal It is common practice to shorten the term "operational amplifier" to op-amp The term operational arose because, before the era of digital computers, such amplifiers were used in analog computers to perform the operations of scalar multiplication, sign inversion, summation, integration and differentiation for the solution of differential equations Nowadays, they are considered to be general active elements for analogue circuit design and have many different applications 1.2 Op-amp Definition We may define the op-amp to be a grounded VCVS with a voltage gain (µ) that is infinite The circuit symbol for the op-amp is as follows: An equivalent circuit, in the form of a VCVS is as follows: The three terminal voltages v+, v–, and vo are all node voltages relative to ground When we analyze a circuit containing op-amps, we cannot use the -

Current Source & Source Transformation Notes
EE301 – CURRENT SOURCES / SOURCE CONVERSION Learning Objectives a. Analyze a circuit consisting of a current source, voltage source and resistors b. Convert a current source and a resister into an equivalent circuit consisting of a voltage source and a resistor c. Evaluate a circuit that contains several current sources in parallel Ideal sources An ideal source is an active element that provides a specified voltage or current that is completely independent of other circuit elements. DC Voltage DC Current Source Source Constant Current Sources The voltage across the current source (Vs) is dependent on how other components are connected to it. Additionally, the current source voltage polarity does not have to follow the current source’s arrow! 1 Example: Determine VS in the circuit shown below. Solution: 2 Example: Determine VS in the circuit shown above, but with R2 replaced by a 6 k resistor. Solution: 1 8/31/2016 EE301 – CURRENT SOURCES / SOURCE CONVERSION 3 Example: Determine I1 and I2 in the circuit shown below. Solution: 4 Example: Determine I1 and VS in the circuit shown below. Solution: Practical voltage sources A real or practical source supplies its rated voltage when its terminals are not connected to a load (open- circuited) but its voltage drops off as the current it supplies increases. We can model a practical voltage source using an ideal source Vs in series with an internal resistance Rs. Practical current source A practical current source supplies its rated current when its terminals are short-circuited but its current drops off as the load resistance increases. We can model a practical current source using an ideal current source in parallel with an internal resistance Rs. -

Circuit Elements Basic Circuit Elements
CHAPTER 2: Circuit Elements Basic circuit elements • Voltage sources, • Current sources, • Resistors, • Inductors, • Capacitors We will postpone introducing inductors and capacitors until Chapter 6, because their use requires that you solve integral and differential equations. 2.1 Voltage and Current Sources • An electrical source is a device that is capable of converting nonelectric energy to electric energy and vice versa. – A discharging battery converts chemical energy to electric energy, whereas a battery being charged converts electric energy to chemical energy. – A dynamo is a machine that converts mechanical energy to electric energy and vice versa. • If operating in the mechanical-to-electric mode, it is called a generator. • If transforming from electric to mechanical energy, it is referred to as a motor. • The important thing to remember about these sources is that they can either deliver or absorb electric power, generally maintaining either voltage or current. 2.1 Voltage and Current Sources • An ideal voltage source is a circuit element that maintains a prescribed voltage across its terminals regardless of the current flowing in those terminals. • Similarly, an ideal current source is a circuit element that maintains a prescribed current through its terminals regardless of the voltage across those terminals. • These circuit elements do not exist as practical devices—they are idealized models of actual voltage and current sources. 2.1 Voltage and Current Sources • Ideal voltage and current sources can be further described as either independent sources or dependent sources. An independent source establishes a voltage or current in a circuit without relying on voltages or currents elsewhere in the circuit. -
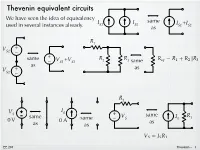
Thevenin Equivalent Circuits
Thevenin equivalent circuits We have seen the idea of equivalency same IS1 IS2 I +I used in several instances already. as S1 S2 R1 V + S1 – + same V +V R R = + – S1 S2 2 3 same as V + as S2 – R1 V IS S + V same R same same – S IS 1 0 V 0 A as as as = EE 201 Thevenin – 1 The behavior of any circuit, with respect to a pair of terminals (port) can be represented with a Thevenin equivalent, which consists of a voltage source in series with a resistor. load some two terminals some + R v circuit (two nodes) = circuit L RL port – RTh RTh load + + Thevenin + V V R v Th – equivalent Th – L RL – Need to determine VTh and RTh so that the model behaves just like the original. EE 201 Thevenin – 2 Norton equivalent load load some + + I v circuit vRL N RN RL – – Ideas developed independently (Thevenin in 1880’s and Norton in 1920’s). But we recognize the two forms as identical because they are source transformations of each other. In EE 201, we won’t make a distinction between the methods for finding Thevenin and Norton. Find one and we have the other. RTh = + V IN R Th – N = EE 201 Thevenin – 3 Example R 1.5 k! 1 RTh 1 k! V R I R R S + 2 S L V + L 9V – 3 k! 6 mA Th – 12 V Attach various load resistors to the R v i P original circuit. Do the same for 1 ! 11.99 mV 11.99 mA 0.144 mW the equivalent circuit. -

IR Temperature Sensor
IR Temperature Sensor By Kika Arias & Elaine Ng MIT 6.101 Final Project Spring 2020 1 Introduction (Kika) The goal of our project is to build an infrared thermometer which is a device that is used to measure the emitted energy from the surface of an object. IR thermometers are used in medical, industrial and home settings for a wide variety of applications. Many electronics retailers sell IR thermometer sensors that perform all of the processing to produce a temperature reading. We wanted to dissect this “black box” to understand how waves of energy can become a human readable temperature. We learned that IR thermometers consist of three basic stages. A sensing stage, in which IR radiation is converted to an electrical signal, a signal conditioning stage, where filtering, amplification, and linearization are performed, and a digital output stage, where the analog signal is converted into a digital one. Our project replicates these basic stages to create a simulated IR temperature sensor. System Overview (Kika) Fig 1. System Block Diagram. Thermopile signal processing in red, and temperature calculation and digital output in purple. As mentioned in the previous section, an IR thermometer consists of three basic stages: sensing, signal conditioning, and digital output. Figure 1 shows our system block diagram with the sensing and signal conditioning stages shown in red, and the digital output and additional processing shown in purple. The sensing stage of our project uses a thermopile sensor which has a negative temperature coefficient (NTC) thermistor for temperature compensation. The thermopile sensor absorbs infrared radiation and converts the IR to a small voltage (typically on the order of μVs). -

Chapter 2: Circuit Elements
Chapter 2: Circuit Elements Objectives o Understand concept of basic circuit elements . Resistor, voltage source, current source, capacitor, inductor o Learn to apply KVL, KCL, Ohm’s Law . Sign conventions Homework/Quiz/Exam Prep o When do we have enough equations? o Math requirements . Simultaneous linear algebraic equations Presentation o Ideal Basic Circuit Elements . Sources: Dependent and Independent . R, L, C o Resistors . Ohm’s Law . Power o Flashlight Circuit . KVL, KCL, Ohm . KVL shortcut o Special Cases . Short circuit; Open circuit . What happens to resistors that are shorted/opened? Activity: worksheet on KVL, KCL, Ohm Activity: sample problems Chapter 2: Circuit Elements There are five Ideal Basic Circuit Elements. We listed these in the previous chapter; we discuss them further here. The Ideal Basic Circuit Elements are as follows. Voltage source Current source Resistor Capacitor Inductor These circuit elements are used to model electrical systems, as we discussed in Chapter 1. They are available in the laboratory, but the ones in the lab are not “ideal”; they are “real”. When we draw circuit models on the board or in quizzes and exams, we assume that ideal elements are intended, unless otherwise stated. To solve circuits involving capacitors and inductors, we require differential equations. Therefore we will postpone these circuit elements until later in the course and deal for the moment with sources and resistors only. 2.1 Sources Source: a device capable of conversion between non-electrical energy and electrical energy. Examples… Generator: mechanical electrical Motor: electrical mechanical Important: energy and power can be either delivered or absorbed, depending on the circuit element and how it is connected into the circuit. -

1. Characteristics and Parameters of Operational Amplifiers
1. CHARACTERISTICS AND PARAMETERS OF OPERATIONAL AMPLIFIERS The characteristics of an ideal operational amplifier are described first, and the characteristics and performance limitations of a practical operational amplifier are described next. There is a section on classification of operational amplifiers and some notes on how to select an operational amplifier for an application. 1.1 IDEAL OPERATIONAL AMPLIFIER 1.1.1 Properties of An Ideal Operational Amplifier The characteristics or the properties of an ideal operational amplifier are: i. Infinite Open Loop Gain, ii. Infinite Input Impedance, iii. Zero Output Impedance, iv. Infinite Bandwidth, v. Zero Output Offset, and vi. Zero Noise Contribution. The opamp, an abbreviation for the operational amplifier, is the most important linear IC. The circuit symbol of an opamp shown in Fig. 1.1. The three terminals are: the non-inverting input terminal, the inverting input terminal and the output terminal. The details of power supply are not shown in a circuit symbol. 1.1.2 Infinite Open Loop Gain From Fig.1.1, it is found that vo = - Ao × vi, where `Ao' is known as the open-loop 5 gain of the opamp. Let vo be -10 Volts, and Ao be 10 . Then vi is 100 :V. Here 1 the input voltage is very small compared to the output voltage. If Ao is very large, vi is negligibly small for a finite vo. For the ideal opamp, Ao is taken to be infinite in value. That means, for an ideal opamp vi = 0 for a finite vo. Typical values of Ao range from 20,000 in low-grade consumer audio-range opamps to more than 2,000,000 in premium grade opamps ( typically 200,000 to 300,000). -

Implementing Voltage Controlled Current Source in Electromagnetic Full-Wave Simulation Using the FDTD Method Khaled Elmahgoub and Atef Z
Implementing Voltage Controlled Current Source in Electromagnetic Full-Wave Simulation using the FDTD Method Khaled ElMahgoub and Atef Z. Elsherbeni Center of Applied Electromagnetic System Research (CAESR), Department of Electrical Engineering, The University of Mississippi, University, Mississippi, USA. [email protected] and [email protected] Abstract — The implementation of a voltage controlled FDTD is introduced with efficient use of both memory and current source (VCCS) in full-wave electromagnetic simulation computational time. This new approach can be used to analyze using finite-difference time-domain (FDTD) is introduced. The VCCS is used to model a metal oxide semiconductor field effect circuits including VCCS or circuits include devices such as transistor (MOSFET) commonly used in microwave circuits. This MOSFETs and BJTs using their equivalent circuit models. To new approach is verified with several numerical examples the best of the authors’ knowledge, the implementation of including circuits with VCCS and MOSFET. Good agreement is dependent sources using FDTD has not been adequately obtained when the results are compared with those based on addressed before. In addition, in most of the previous work the analytical solution and PSpice. implementation of nonlinear devices such as transistors has Index Terms — Finite-difference time-domain, dependent been handled using FDTD-SPICE models or by importing the sources, voltage controlled current source, MOSFET. S-parameters from another technique to the FDTD simulation [2]-[7]. In this work the implementation of the VCCS in I. INTRODUCTION FDTD will be used to simulate a MOSFET with its equivalent The finite-difference time-domain (FDTD) method has gained model without the use of external tools, the entire simulation great popularity as a tool used for electromagnetic can be done using the FDTD. -

Electrical Engineering Dictionary
ratio of the power per unit solid angle scat- tered in a specific direction of the power unit area in a plane wave incident on the scatterer R from a specified direction. RADHAZ radiation hazards to personnel as defined in ANSI/C95.1-1991 IEEE Stan- RS commonly used symbol for source dard Safety Levels with Respect to Human impedance. Exposure to Radio Frequency Electromag- netic Fields, 3 kHz to 300 GHz. RT commonly used symbol for transfor- mation ratio. radial basis function network a fully R-ALOHA See reservation ALOHA. connected feedforward network with a sin- gle hidden layer of neurons each of which RL Typical symbol for load resistance. computes a nonlinear decreasing function of the distance between its received input and Rabi frequency the characteristic cou- a “center point.” This function is generally pling strength between a near-resonant elec- bell-shaped and has a different center point tromagnetic field and two states of a quan- for each neuron. The center points and the tum mechanical system. For example, the widths of the bell shapes are learned from Rabi frequency of an electric dipole allowed training data. The input weights usually have transition is equal to µE/hbar, where µ is the fixed values and may be prescribed on the electric dipole moment and E is the maxi- basis of prior knowledge. The outputs have mum electric field amplitude. In a strongly linear characteristics, and their weights are driven 2-level system, the Rabi frequency is computed during training. equal to the rate at which population oscil- lates between the ground and excited states.