Logic, Words, and Integers
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Bit Nove Signal Interface Processor
www.audison.eu bit Nove Signal Interface Processor POWER SUPPLY CONNECTION Voltage 10.8 ÷ 15 VDC From / To Personal Computer 1 x Micro USB Operating power supply voltage 7.5 ÷ 14.4 VDC To Audison DRC AB / DRC MP 1 x AC Link Idling current 0.53 A Optical 2 sel Optical In 2 wire control +12 V enable Switched off without DRC 1 mA Mem D sel Memory D wire control GND enable Switched off with DRC 4.5 mA CROSSOVER Remote IN voltage 4 ÷ 15 VDC (1mA) Filter type Full / Hi pass / Low Pass / Band Pass Remote OUT voltage 10 ÷ 15 VDC (130 mA) Linkwitz @ 12/24 dB - Butterworth @ Filter mode and slope ART (Automatic Remote Turn ON) 2 ÷ 7 VDC 6/12/18/24 dB Crossover Frequency 68 steps @ 20 ÷ 20k Hz SIGNAL STAGE Phase control 0° / 180° Distortion - THD @ 1 kHz, 1 VRMS Output 0.005% EQUALIZER (20 ÷ 20K Hz) Bandwidth @ -3 dB 10 Hz ÷ 22 kHz S/N ratio @ A weighted Analog Input Equalizer Automatic De-Equalization N.9 Parametrics Equalizers: ±12 dB;10 pole; Master Input 102 dBA Output Equalizer 20 ÷ 20k Hz AUX Input 101.5 dBA OPTICAL IN1 / IN2 Inputs 110 dBA TIME ALIGNMENT Channel Separation @ 1 kHz 85 dBA Distance 0 ÷ 510 cm / 0 ÷ 200.8 inches Input sensitivity Pre Master 1.2 ÷ 8 VRMS Delay 0 ÷ 15 ms Input sensitivity Speaker Master 3 ÷ 20 VRMS Step 0,08 ms; 2,8 cm / 1.1 inch Input sensitivity AUX Master 0.3 ÷ 5 VRMS Fine SET 0,02 ms; 0,7 cm / 0.27 inch Input impedance Pre In / Speaker In / AUX 15 kΩ / 12 Ω / 15 kΩ GENERAL REQUIREMENTS Max Output Level (RMS) @ 0.1% THD 4 V PC connections USB 1.1 / 2.0 / 3.0 Compatible Microsoft Windows (32/64 bit): Vista, INPUT STAGE Software/PC requirements Windows 7, Windows 8, Windows 10 Low level (Pre) Ch1 ÷ Ch6; AUX L/R Video Resolution with screen resize min. -

Signedness-Agnostic Program Analysis: Precise Integer Bounds for Low-Level Code
Signedness-Agnostic Program Analysis: Precise Integer Bounds for Low-Level Code Jorge A. Navas, Peter Schachte, Harald Søndergaard, and Peter J. Stuckey Department of Computing and Information Systems, The University of Melbourne, Victoria 3010, Australia Abstract. Many compilers target common back-ends, thereby avoid- ing the need to implement the same analyses for many different source languages. This has led to interest in static analysis of LLVM code. In LLVM (and similar languages) most signedness information associated with variables has been compiled away. Current analyses of LLVM code tend to assume that either all values are signed or all are unsigned (except where the code specifies the signedness). We show how program analysis can simultaneously consider each bit-string to be both signed and un- signed, thus improving precision, and we implement the idea for the spe- cific case of integer bounds analysis. Experimental evaluation shows that this provides higher precision at little extra cost. Our approach turns out to be beneficial even when all signedness information is available, such as when analysing C or Java code. 1 Introduction The “Low Level Virtual Machine” LLVM is rapidly gaining popularity as a target for compilers for a range of programming languages. As a result, the literature on static analysis of LLVM code is growing (for example, see [2, 7, 9, 11, 12]). LLVM IR (Intermediate Representation) carefully specifies the bit- width of all integer values, but in most cases does not specify whether values are signed or unsigned. This is because, for most operations, two’s complement arithmetic (treating the inputs as signed numbers) produces the same bit-vectors as unsigned arithmetic. -

Metaclasses: Generative C++
Metaclasses: Generative C++ Document Number: P0707 R3 Date: 2018-02-11 Reply-to: Herb Sutter ([email protected]) Audience: SG7, EWG Contents 1 Overview .............................................................................................................................................................2 2 Language: Metaclasses .......................................................................................................................................7 3 Library: Example metaclasses .......................................................................................................................... 18 4 Applying metaclasses: Qt moc and C++/WinRT .............................................................................................. 35 5 Alternatives for sourcedefinition transform syntax .................................................................................... 41 6 Alternatives for applying the transform .......................................................................................................... 43 7 FAQs ................................................................................................................................................................. 46 8 Revision history ............................................................................................................................................... 51 Major changes in R3: Switched to function-style declaration syntax per SG7 direction in Albuquerque (old: $class M new: constexpr void M(meta::type target, -

Meta-Class Features for Large-Scale Object Categorization on a Budget
Meta-Class Features for Large-Scale Object Categorization on a Budget Alessandro Bergamo Lorenzo Torresani Dartmouth College Hanover, NH, U.S.A. faleb, [email protected] Abstract cation accuracy over a predefined set of classes, and without consideration of the computational costs of the recognition. In this paper we introduce a novel image descriptor en- We believe that these two assumptions do not meet the abling accurate object categorization even with linear mod- requirements of modern applications of large-scale object els. Akin to the popular attribute descriptors, our feature categorization. For example, test-recognition efficiency is a vector comprises the outputs of a set of classifiers evaluated fundamental requirement to be able to scale object classi- on the image. However, unlike traditional attributes which fication to Web photo repositories, such as Flickr, which represent hand-selected object classes and predefined vi- are growing at rates of several millions new photos per sual properties, our features are learned automatically and day. Furthermore, while a fixed set of object classifiers can correspond to “abstract” categories, which we name meta- be used to annotate pictures with a set of predefined tags, classes. Each meta-class is a super-category obtained by the interactive nature of searching and browsing large im- grouping a set of object classes such that, collectively, they age collections calls for the ability to allow users to define are easy to distinguish from other sets of categories. By us- their own personal query categories to be recognized and ing “learnability” of the meta-classes as criterion for fea- retrieved from the database, ideally in real-time. -
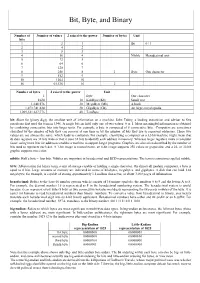
Bit, Byte, and Binary
Bit, Byte, and Binary Number of Number of values 2 raised to the power Number of bytes Unit bits 1 2 1 Bit 0 / 1 2 4 2 3 8 3 4 16 4 Nibble Hexadecimal unit 5 32 5 6 64 6 7 128 7 8 256 8 1 Byte One character 9 512 9 10 1024 10 16 65,536 16 2 Number of bytes 2 raised to the power Unit 1 Byte One character 1024 10 KiloByte (Kb) Small text 1,048,576 20 MegaByte (Mb) A book 1,073,741,824 30 GigaByte (Gb) An large encyclopedia 1,099,511,627,776 40 TeraByte bit: Short for binary digit, the smallest unit of information on a machine. John Tukey, a leading statistician and adviser to five presidents first used the term in 1946. A single bit can hold only one of two values: 0 or 1. More meaningful information is obtained by combining consecutive bits into larger units. For example, a byte is composed of 8 consecutive bits. Computers are sometimes classified by the number of bits they can process at one time or by the number of bits they use to represent addresses. These two values are not always the same, which leads to confusion. For example, classifying a computer as a 32-bit machine might mean that its data registers are 32 bits wide or that it uses 32 bits to identify each address in memory. Whereas larger registers make a computer faster, using more bits for addresses enables a machine to support larger programs. -

Floating Point Arithmetic
Systems Architecture Lecture 14: Floating Point Arithmetic Jeremy R. Johnson Anatole D. Ruslanov William M. Mongan Some or all figures from Computer Organization and Design: The Hardware/Software Approach, Third Edition, by David Patterson and John Hennessy, are copyrighted material (COPYRIGHT 2004 MORGAN KAUFMANN PUBLISHERS, INC. ALL RIGHTS RESERVED). Lec 14 Systems Architecture 1 Introduction • Objective: To provide hardware support for floating point arithmetic. To understand how to represent floating point numbers in the computer and how to perform arithmetic with them. Also to learn how to use floating point arithmetic in MIPS. • Approximate arithmetic – Finite Range – Limited Precision • Topics – IEEE format for single and double precision floating point numbers – Floating point addition and multiplication – Support for floating point computation in MIPS Lec 14 Systems Architecture 2 Distribution of Floating Point Numbers e = -1 e = 0 e = 1 • 3 bit mantissa 1.00 X 2^(-1) = 1/2 1.00 X 2^0 = 1 1.00 X 2^1 = 2 1.01 X 2^(-1) = 5/8 1.01 X 2^0 = 5/4 1.01 X 2^1 = 5/2 • exponent {-1,0,1} 1.10 X 2^(-1) = 3/4 1.10 X 2^0 = 3/2 1.10 X 2^1= 3 1.11 X 2^(-1) = 7/8 1.11 X 2^0 = 7/4 1.11 X 2^1 = 7/2 0 1 2 3 Lec 14 Systems Architecture 3 Floating Point • An IEEE floating point representation consists of – A Sign Bit (no surprise) – An Exponent (“times 2 to the what?”) – Mantissa (“Significand”), which is assumed to be 1.xxxxx (thus, one bit of the mantissa is implied as 1) – This is called a normalized representation • So a mantissa = 0 really is interpreted to be 1.0, and a mantissa of all 1111 is interpreted to be 1.1111 • Special cases are used to represent denormalized mantissas (true mantissa = 0), NaN, etc., as will be discussed. -

OMG Meta Object Facility (MOF) Core Specification
Date : October 2019 OMG Meta Object Facility (MOF) Core Specification Version 2.5.1 OMG Document Number: formal/2019-10-01 Standard document URL: https://www.omg.org/spec/MOF/2.5.1 Normative Machine-Readable Files: https://www.omg.org/spec/MOF/20131001/MOF.xmi Informative Machine-Readable Files: https://www.omg.org/spec/MOF/20131001/CMOFConstraints.ocl https://www.omg.org/spec/MOF/20131001/EMOFConstraints.ocl Copyright © 2003, Adaptive Copyright © 2003, Ceira Technologies, Inc. Copyright © 2003, Compuware Corporation Copyright © 2003, Data Access Technologies, Inc. Copyright © 2003, DSTC Copyright © 2003, Gentleware Copyright © 2003, Hewlett-Packard Copyright © 2003, International Business Machines Copyright © 2003, IONA Copyright © 2003, MetaMatrix Copyright © 2015, Object Management Group Copyright © 2003, Softeam Copyright © 2003, SUN Copyright © 2003, Telelogic AB Copyright © 2003, Unisys USE OF SPECIFICATION - TERMS, CONDITIONS & NOTICES The material in this document details an Object Management Group specification in accordance with the terms, conditions and notices set forth below. This document does not represent a commitment to implement any portion of this specification in any company's products. The information contained in this document is subject to change without notice. LICENSES The companies listed above have granted to the Object Management Group, Inc. (OMG) a nonexclusive, royalty-free, paid up, worldwide license to copy and distribute this document and to modify this document and distribute copies of the modified version. Each of the copyright holders listed above has agreed that no person shall be deemed to have infringed the copyright in the included material of any such copyright holder by reason of having used the specification set forth herein or having conformed any computer software to the specification. -

Handwritten Digit Classication Using 8-Bit Floating Point Based Convolutional Neural Networks
Downloaded from orbit.dtu.dk on: Apr 10, 2018 Handwritten Digit Classication using 8-bit Floating Point based Convolutional Neural Networks Gallus, Michal; Nannarelli, Alberto Publication date: 2018 Document Version Publisher's PDF, also known as Version of record Link back to DTU Orbit Citation (APA): Gallus, M., & Nannarelli, A. (2018). Handwritten Digit Classication using 8-bit Floating Point based Convolutional Neural Networks. DTU Compute. (DTU Compute Technical Report-2018, Vol. 01). General rights Copyright and moral rights for the publications made accessible in the public portal are retained by the authors and/or other copyright owners and it is a condition of accessing publications that users recognise and abide by the legal requirements associated with these rights. • Users may download and print one copy of any publication from the public portal for the purpose of private study or research. • You may not further distribute the material or use it for any profit-making activity or commercial gain • You may freely distribute the URL identifying the publication in the public portal If you believe that this document breaches copyright please contact us providing details, and we will remove access to the work immediately and investigate your claim. Handwritten Digit Classification using 8-bit Floating Point based Convolutional Neural Networks Michal Gallus and Alberto Nannarelli (supervisor) Danmarks Tekniske Universitet Lyngby, Denmark [email protected] Abstract—Training of deep neural networks is often con- In order to address this problem, this paper proposes usage strained by the available memory and computational power. of 8-bit floating point instead of single precision floating point This often causes it to run for weeks even when the underlying which allows to save 75% space for all trainable parameters, platform is employed with multiple GPUs. -

Bit Preservation
Just keep the bits: an introduction to bit level preservation Just keep the bits… What are the risks? (1) • Media obsolescence • Media failure or decay (such as “bit rot”) • Natural / human-made disaster Images by Aldric Rodríguez Iborra, Erin Standley, Marie Van den Broeck, Edward Boatman and Dilon Choudhury from the Noun Project What is the result? Image courtesy of the British Library How do we solve these problems? • As a minimum: • Keep more than one copy • Refresh storage media • Integrity check your data (also called “Fixity”) What is a “checksum” or “hash value”? the past 02ace44afd49e9a522c9f14c7d89c3e9 A less pleasant the future 02ace44afd49e9a522c9f14c7d89c3e902ace11afd49e9a522c9f14c7d79c3e2 future Image by Arthur Shlain from the Noun Project Combined strategies: keep 3 copies and perform integrity checks Integrity checking - tools • Fixity • https://www.avpreserve.com/tools/fixity/ • Auditing Control Environment (ACE) • https://wiki.umiacs.umd.edu/adapt/index.php/Ace • For alternatives – see COPTR • http://coptr.digipres.org/Category:Fixity Data storage – some options • Hard disk, magnetic tape or optical disc • Consumer hand held media • Managed storage • Cloud Long lived media: a red herring “…announcements of very long-lived media have made no practical difference to large-scale digital preservation…” David Rosenthal, Stanford University Library http://blog.dshr.org/2013/07/immortal-media.html What are the risks? (2) • Common mode failure (technology) • Human error and malicious damage Recap • Keep several copies of all -

10 Disruptive Trends in Wealth Management
10 Disruptive trends in wealth management 10 Disruptive trends in wealth management i 1 Introduction Wealth Management (WM)1 is one of the most attractive The WM industry is in the midst of significant change: sectors within financial services for at least two reasons: a new generation of investors, whose expectations and First, WM businesses tend to have greater growth preferences have been shaped by new technologies prospects, lower capital requirements, and a higher return and by their living through the last financial crisis, have on equity (ROE) than most other retail banking businesses, brought new standards to the industry in terms of how hence their appeal to diversified financial services firms at a advice and investment products are being delivered. These time when capital is viewed as more expensive, growth is new investors will control an increasing share of US retail hard to come by, and equity returns for the banking industry assets over the next decade. Furthermore, a challenging are close to the cost of capital. Second, WM offerings investment environment, characterized by increased levels are essential to attracting and retaining profitable retail of uncertainty and rising costs of risk to investors and WM customers. For instance, based on our experience, mass firms alike is making it harder for advisors to generate affluent customers can typically represent 80% or more of superior investment performance for their clients. Shifting the net income generated by retail banks and they often demographics with the aging of advisors and an upcoming regard their relationship with a provider of WM services as transfer of wealth from baby boomers to their children their most important financial relationship. -

CS/COE1541: Introduction to Computer Architecture Dept
CS/COE1541: Introduction to Computer Architecture Dept. of Computer Science University of Pittsburgh http://www.cs.pitt.edu/~melhem/courses/1541p/index.html Chapter 5: Exploiting the Memory Hierarchy Lecture 2 Lecturer: Rami Melhem 1 The Basics of Caches • Until specified otherwise, it will be assumed that a block is one word of data • Three issues: – How do we know if a data item is in the cache? – If it is, how do we find it? address – If it is not, what do we do? Main CPU Cache memory • It boils down to – where do we put an item in the cache? – how do we identify the items in the cache? data • Two solutions – put item anywhere in cache (associative cache) – associate specific locations to specific items (direct mapped cache) Note: we will assume that memory requests are for words (4 Bytes) although an instruction can address a byte 2 Fully associative cache 00000 00001 To cache a data word, d, whose memory address is L: 00010 00011 •Put d in any location in the cache 00100 00101 • Tag the data with the memory address L. 00110 00111 01000 Cache index 01001 01010 01011 000 01001000 01100 Example: 001 001 01101 010 010 01110 • An 8-word cache 011 011 01111 (indexed by 000, … , 111) 100 11000100 10000 101 101 10001 • A 32-words memory 110 01110110 10010 111 111 10011 (addresses 00000, … , 11111) Tags Data 10100 10101 Cache 10110 10111 11000 Advantage: can fully utilize the cache capacity 11001 11010 Disadvantage: need to search all tags to find data 11011 11100 Memory word addresses 11101 11110 (without the 2-bits byte offset) 11111 Memory 3 Direct Mapped Cache (direct hashing) 00000 Assume that the size of the cache is N words. -

Python 3 Metaprogramming Requirements
Python 3 Metaprogramming David Beazley @dabeaz http://www.dabeaz.com Presented at PyCon'2013, Santa Clara, CA March 14, 2013 Copyright (C) 2013, http://www.dabeaz.com 1 Requirements • Python 3.3 or more recent • Don't even attempt on any earlier version • Support files: http://www.dabeaz.com/py3meta Copyright (C) 2013, http://www.dabeaz.com 2 Welcome! • An advanced tutorial on two topics • Python 3 • Metaprogramming • Honestly, can you have too much of either? • No! Copyright (C) 2013, http://www.dabeaz.com 3 Metaprogramming • In a nutshell: code that manipulates code • Common examples: • Decorators • Metaclasses • Descriptors • Essentially, it's doing things with code Copyright (C) 2013, http://www.dabeaz.com 4 Why Would You Care? • Extensively used in frameworks and libraries • Better understanding of how Python works • It's fun • It solves a practical problem Copyright (C) 2013, http://www.dabeaz.com 5 DRY Copyright (C) 2013, http://www.dabeaz.com 6 DRY Don't Repeat Yourself Copyright (C) 2013, http://www.dabeaz.com 7 DRY Don't Repeat Yourself Don't Repeat Yourself Copyright (C) 2013, http://www.dabeaz.com 8 Don't Repeat Yourself • Highly repetitive code sucks • Tedious to write • Hard to read • Difficult to modify Copyright (C) 2013, http://www.dabeaz.com 9 This Tutorial • A modern journey of metaprogramming • Highlight unique aspects of Python 3 • Explode your brain Copyright (C) 2013, http://www.dabeaz.com 10 Target Audience • Framework/library builders • Anyone who wants to know how things work • Programmers wishing to increase "job security" Copyright (C) 2013, http://www.dabeaz.com 11 Reading • Tutorial loosely based on content in "Python Cookbook, 3rd Ed." • Published May, 2013 • You'll find even more information in the book Copyright (C) 2013, http://www.dabeaz.com 12 Preliminaries Copyright (C) 2013, http://www.dabeaz.com 13 Basic Building Blocks statement1 def func(args): statement2 statement1 statement3 statement2 ..