Introducing Young Children to Complex Systems Through Modelling
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
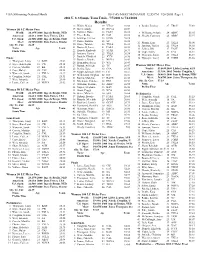
2004 Olympic Trials Results
USA Swimming-National Meets Hy-Tek's MEET MANAGER 12:55 PM 1/26/2005 Page 1 2004 U. S. Olympic Team Trials - 7/7/2004 to 7/14/2004 Results 13 Walsh, Mason 19 VTAC 26.08 8 Benko, Lindsay 27 TROJ 55.69 Women 50 LC Meter Free 15 Silver, Emily 18 NOVA 26.09 World: 24.13W 2000 Inge de Bruijn, NED 16 Vollmer, Dana 16 FAST 26.12 9 Williams, Stefanie 24 ABSC 55.95 American: 24.63A 2000 Dara Torres, USA 17 Price, Keiko 25 CAL 26.16 10 Shealy, Courtney 26 ABSC 55.97 18 Jennings, Emilee 15 KING 26.18 U.S. Open: 24.50O 2000 Inge de Bruijn, NED 19 Radke, Katrina 33 SC 26.22 Meet: 24.90M 2000 Dara Torres, Stanfor 11 Phenix, Erin 23 TXLA 56.00 20 Stone, Tammie 28 TXLA 26.23 Oly. Tr. Cut: 26.39 12 Jamison, Tanica 22 TXLA 56.02 21 Boutwell, Lacey 21 PASA 26.29 Name Age Team 13 Jeffrey, Rhi 17 FAST 56.09 22 Harada, Kimberly 23 STAR 26.33 Finals Time 14 Cope, Haley 25 CAJ 56.11 23 Jamison, Tanica 22 TXLA 26.34 15 Wanezek, Sarah 21 TXLA 56.19 24 Daniels, Elizabeth 22 JCCS 26.36 Finals 16 Nymeyer, Lacey 18 FORD 56.56 25 Boncher, Brooke 21 NOVA 26.42 1 Thompson, Jenny 31 BAD 25.02 26 Hernandez, Sarah 19 WA 26.43 2 Joyce, Kara Lynn 18 CW 25.11 27 Bastak, Ashleigh 22 TC 26.47 Women 100 LC Meter Free 3 Correia, Maritza 22 BA 25.15 28 Denby, Kara 18 CSA 26.50 World: 53.66W 2004 Libby Lenton, AUS 4 Cope, Haley 25 CAJ 25.22 29 Ripple Johnston, Shell 23 ES 26.51 American: 53.99A 2002 Natalie Coughlin, U 5 Wanezek, Sarah 21 TXLA 25.27 29 Medendorp, Meghan 22 IST 26.51 U.S. -

Preparation of Sprint Swimmers
SWIMMING IN AUSTRALIA – November-December 2003 In this presentation I would like to share my PREPARATION OF experience in developing Michael Klim’s talent. Reflecting back on the 1998 World SPRINT SWIMMERS Championships and the way we approached the By Gennadi Touretski plan, I realise that since 1993 when I first met Presented at ASCTA 1998 Convention Michael I cannot recall a single occasion when he was significantly off track or disappointed in his progress. His motivation and dedication to INTRODUCTION training during this period was extremely high. Since this time, he has swum some 8,000km in The Men’s 100m Freestyle is regarded as the the pool with almost 500 races in his quest to blue riband event of the Olympic Swimming, become the number one swimmer in the world. World Championships, with many gold medallists becoming household names. It has Many people have asked me the key to lead to two Olympic champions to movie fame: Michael’s success. The answer is always the most notably Johnny Weissmuller in the role of same: natural talent coupled with the ability to Tarzan. He won two successive Olympic 100m work consistently and adopting a philosophy Freestyle gold medals in the 1920s. that you shouldn’t dive twice into the same water. The only way to win is with non-stop Among the Olympic champions we have two perfection. For developing athletes, the Australians … John Devitt and Michael Wenden personality of the swimmer is extremely who were successful in 1960 and 1968 important and swimming and training with respectively. I have been privileged to coach Aleksandre Popov, the world’s fastest swimmer, Aleksandre Popov the World 100m Freestyle helped Michael to improve his technique and champion in 1994 and 1998, double Olympic educate himself in the way champions should Champion in the 50 and 100m Freestyle in behave. -

Code De Conduite Pour Le Water Polo
HistoFINA SWIMMING MEDALLISTS AND STATISTICS AT OLYMPIC GAMES Last updated in November, 2016 (After the Rio 2016 Olympic Games) Fédération Internationale de Natation Ch. De Bellevue 24a/24b – 1005 Lausanne – Switzerland TEL: (41-21) 310 47 10 – FAX: (41-21) 312 66 10 – E-mail: [email protected] Website: www.fina.org Copyright FINA, Lausanne 2013 In memory of Jean-Louis Meuret CONTENTS OLYMPIC GAMES Swimming – 1896-2012 Introduction 3 Olympic Games dates, sites, number of victories by National Federations (NF) and on the podiums 4 1896 – 2016 – From Athens to Rio 6 Olympic Gold Medals & Olympic Champions by Country 21 MEN’S EVENTS – Podiums and statistics 22 WOMEN’S EVENTS – Podiums and statistics 82 FINA Members and Country Codes 136 2 Introduction In the following study you will find the statistics of the swimming events at the Olympic Games held since 1896 (under the umbrella of FINA since 1912) as well as the podiums and number of medals obtained by National Federation. You will also find the standings of the first three places in all events for men and women at the Olympic Games followed by several classifications which are listed either by the number of titles or medals by swimmer or National Federation. It should be noted that these standings only have an historical aim but no sport signification because the comparison between the achievements of swimmers of different generations is always unfair for several reasons: 1. The period of time. The Olympic Games were not organised in 1916, 1940 and 1944 2. The evolution of the programme. -

1/4/2004 Piscina Olímpica Encantada T
Untitled 1/5/04 10:24 AM Licensed to Natacion Fernando Delgado Hy-Tek's Meet Manager II WINTER TRAINING MEET - 1/4/2004 PISCINA OLÍMPICA ENCANTADA TRUJILLO ALTO, PUERTO RICO Results Event 1 Women Open 200 LC Meter Medley Relay =============================================================================== MEET RECORD: * 2:07.03 1/5/2003 SYRACUSE, SYRACUSE- R Wrede, J Jonusaitis, E McDonough, C Jansen School Seed Finals =============================================================================== 1 NOTRE DAME SWIMMING 'A' 2:00.78 2:05.38* 2 NOTRE DAME SWIMMING 'B' 2:05.85 2:06.39* 3 SYRACUSE ORANGEMEN 'A' 2:04.13 2:07.59 4 YALE 'A' 1:59.10 2:09.30 5 ST'S. JOHNS UNIVERSITY 'A' 1:58.35 2:09.94 6 NADADORES SANTURCE 'A' 2:11.51 2:12.48 7 SETON HALL UNIVERSITY 'A' 2:07.98 2:13.43 8 YALE 'B' 2:03.60 2:13.86 9 ST'S. JOHNS UNIVERSITY 'B' 2:01.50 2:14.43 10 GEORGETOWN SWIMMING 'A' 2:10.33 2:15.81 11 ST'S. JOHNS UNIVERSITY 'C' 2:05.00 2:16.53 12 BRANDIES UNIVERSITY 'A' 3:11.00 2:17.50 13 YALE 'C' 2:05.70 2:17.73 14 SETON HALL UNIVERSITY 'B' 2:15.64 2:20.05 15 NADADORES SANTURCE 'B' 2:15.87 2:20.21 16 NOTRE DAME SWIMMING 'C' 2:10.77 2:22.08 17 GEORGETOWN SWIMMING 'B' 2:14.55 2:22.68 18 MONTCLAIR STATE UNIVERSITY 'A' 2:07.30 2:29.65 19 BRANDIES UNIVERSITY 'B' 3:20.00 2:29.75 Event 2 Men Open 200 LC Meter Medley Relay =============================================================================== MEET RECORD: * 1:53.79 1/5/2003 YALE UNIVERSITY, YALE- School Seed Finals =============================================================================== 1 SETON HALL UNIVERSITY 'A' 1:44.09 1:51.80* 2 YALE 'A' 1:44.30 1:53.18* 3 SYRACUSE ORANGEMEN 'A' 1:46.22 1:54.65 4 NADADORES SANTURCE 'A' 1:58.39 1:55.65 5 NADADORES SANTURCE 'B' 2:02.01 1:56.01 6 YALE 'B' 1:49.70 1:56.66 7 ST'S. -

II~Ny Ore, Continue Their Dominance of Their Respective Events
I'_l .N" l'.l('l FI4' There are different opportunities f II A .~1 I' I qi ~ ~ II I i ~ au'aiting all swimmers the year after an Olympic Games. By BtdD ~i,VmHllnoin.~,~i~ tions' exciting new talent to showcase its potential. Neil Walker, FUKUOKA, Japan--The post-Olympic year provides different op- Lenny Krayzelburg, Mai Nakamura, Grant Hackett, Ian Thorpe and portunities for swimmers. others served notice to the swimming world that they will be a force For the successful Atlanta Olympians, the opportunity to contin- to be reckoned with leading up to the 2000 Sydney Olympics. ue their Olympic form still remains, or they can take a back seat The meet was dominated once again by the U.S. and Australian with a hard-earned break from international competition. teams, who between them took home 31 of the 37 gold medals. For those who turned in disappointing results in Atlanta, there Japan (2), Costa Rica (2), China (i) and Puerto Rico (1) all won was the opportunity to atone for their disappointment and return to gold, while charter nation Canada failed to win an event. world-class form. The increasing gap between the top two nations and other com- And for others, the post-Olympic year provides the opportunity peting countries must be a concern for member federations in an era to break into respective national teams and world ranking lists while when most major international competitions are seeing a more even gaining valuable international racing experience. spread of success among nations. The 1997 Pan Pacific Championships Aug. -

Analysis of Stroke Rates in Freestyle Events at 2000 Olympics
ANALYSIS OF STROKE RATES IN FREESTYLE EVENTS AT 2000 OLYMPICS By David Pyne & Cassie Trewin Department of Physiology, Australian Institute of Sport The aim of this article is to examine the patterns of stroke rates of successful swimmers during the 2000 Sydney Olympic Games. Stroke rates of swimmers in the Final (top 8 swimmers) of selected Freestyle events were taken from the Competition Analysis of the 2000 Olympic Games (courtesy of the Biomechanics Department, Australian Institute of Sport). The stroke rates for each 25, 50 or 100m race split and placing in the 50, 100, 200 and 400 m freestyle events were collated. The interesting questions are … Were there differences in stroke rates between the sprint (50 and 100m) and middle-distance (200 and 400m) events? Were there any differences in stroke rates between the Men’s and Women’s events? How much variation in stroke rate was evident between swimmers in the same event? And how much difference was observed between first and last lap stroke rates compared to the average for the event for each individual swimmer. The individual and mean stroke rates for each of the finalists in the 50, 100, 200 and 400 Freestyle events are presented in Table 1. Statistical analysis (data not shown) indicated that there were no significant correlations between average stroke rate on any lap and final placing. The only exception was the Women’s 400m Freestyle where the placegetters had a significantly higher average stroke rate over the race than those swimmers finishing outside the medals. This indicates that there is considerable variation in stroke rate between different swimmers at the Olympic level. -

Men's All-Time Top 50 World Performers-Performances
Men’s All-Time World Top 50 Performers-Performances’ Rankings Page 111 ο f 727272 MEN’S ALL-TIME TOP 50 WORLD PERFORMERS-PERFORMANCES RANKINGS ** World Record # 2nd-Performance All-Time +* European Record *+ Commonwealth Record *" Latin-South American Record ' U.S. Open Record * National Record r Relay Leadoff Split p Preliminary Time + Olympic Record ^ World Championship Record a Asian Record h Hand time A Altitude-aided 50 METER FREESTYLE Top 51 Performances 20.91** Cesar Augusto Filho Cielo, BRA/Auburn BRA Nationals Sao Paulo 12-18-09 (Reaction Time: +0-66. (Note: first South American swimmer to set 50 free world-record. Fifth man to hold 50-100 meter freestyle world records simultaneously: Others: Matt Biondi [USA], Alexander Popov [RUS], Alain Bernard [FRA], Eamon Sullivan [AUS]. (Note: first time world-record broken in South America. First world-record swum in South America since countryman Da Silva went 26.89p @ the Trofeu Maria Lenk meet in Rio on May 8, 2009. First Brazilian world record-setter in South America: Ricardo Prado, who won 400 IM @ 1982 World Championships in Guayaquil.) 20.94+*# Fred Bousquet, FRA/Auburn FRA Nationals/WCTs Montpellier 04-26-09 (Reaction Time: +0.74. (Note: first world-record of career, first man sub 21.0, first Auburn male world record-setter since America’s Rowdy Gaines [49.36, 100 meter freestyle, Austin, 04/81. Gaines broke his own 200 free wr following summer @ U.S. WCTs.) (Note: Bousquet also first man under 19.0 for 50 yard freestyle [18.74, NCAAs, 2005, Minneapolis]) 21.02p Cielo BRA Nationals Sao Paulo 12-18-09 21.08 Cielo World Championships Rome 08-02-09 (Reaction Time: +0.68. -

Swimming Australia
SWIMMING SPECIAL EDITION IN AUSTRALIA PREVIEW PRESSURE SITUATIONS - NO WORRIES! An ultralight, low resistance racing goggle, the Stealth MKII features extended arms and a 3D seal to relieve pressure on and around the eyes. Stealth MKII Immerse yourself in Vorgee’s full product range at vorgee.com © Delly Carr Swimming Australia Trials, tribulations and testing times for Tokyo as our swimmers face their moments of truth in Adelaide ASCTA engaged swimming media expert Ian Hanson to profile a selection of athletes that will line up in Adelaide from June 12-17 for the 2021 Australian Swimming Trials at the SA Aquatic & Leisure Centre, after a frantic and frenetic time where Selection Criteria has changed with the inclusion of contingencies and recent lockdowns, forcing WA and Victorian Olympic and Paralympic hopefuls into Queensland. It will be a testing Trials in more ways than one - for swimmers, coaches and event staff as they work round the clock to give the class of 2020-21 a crack at their Olympic and Paralympic dreams. Here Ian Hanson provides his insight into the events that will seal the Tokyo team for the Games. Please enjoy and we wish the best of luck to all coaches and athletes at the Australian Swimming Trials. WOMEN 2021 © Delly Carr Swimming Australia WOMEN 50m Freestyle WORLD RECORD: Sarah Sjostrom, Sweden, 23.67 (2017) AUSTRALIAN RECORD: Cate Campbell, 23.78 (2018) Olympic QT: 24.46 Preview: An event shared at Australian Championship level by the Campbell sisters from Knox Pymble (Coach: Simon Cusack) since Cate Campbell won her first Australian title in 2012 - the first of her seven National championship wins. -

Aus Men Top 25 Lc, 1 Jan to 23 Dec 2010
Australian Men Top 25 Long Course 1st January to 23 December 2010 email any errors or omissions to [email protected] FPS Male 50 Free * 22.09 L 921 F Eamon Sullivan 24 AUS 18/06/2010 Pescara, Italy * 22.09 L 921 F Ashley Callus 31 NTEND 16/03/2010 2010 Telstra Australian Championships 22.28 L 897 S Cameron Prosser 25 AUS 3/10/2010 Commonwealth Games - Delhi 22.39 L 884 S Matthew Abood 23 SYDU 16/03/2010 2010 Telstra Australian Championships 22.44 L 878 P Kyle Richardson 23 AUS 18/08/2010 Pan Pacific Championships 22.48 L 874 P Te Haumi Maxwell 16 AUS 26/08/2010 Junior Pan Pacific Championships 22.49 L 872 F Kenneth To 18 AUS 26/08/2010 Junior Pan Pacific Championships 22.66 L 853 F Matt Targett 24 MVC 16/03/2010 2010 Telstra Australian Championships 22.75 L 843 P James Magnussen 19 AUS 18/08/2010 Pan Pacific Championships * 22.86 L 831 F James Roberts 18 NTEND 5/04/2010 2010 Australian Age Championships * 22.86 L 831 S Hamish Rose 19 CPER 16/03/2010 2010 Telstra Australian Championships 22.87 L 830 S Steve Neuwert 25 WSS 16/03/2010 2010 Telstra Australian Championships 23.00 L 816 S Jonathon Newton 29 SYDU 16/03/2010 2010 Telstra Australian Championships * 23.08 L 807 F Joel Alati 17 CAA 15/01/2010 2010 Open SWD Victorian Championships * 23.08 L 807 P Kenrick Monk 22 AUS 18/08/2010 Pan Pacific Championships 23.09 L 806 F Hayden Stoeckel 25 NWD 5/06/2010 2010 SA Division 1 Complete Series * 23.16 L 799 P Andrew Abood 19 KNGC 16/03/2010 2010 Telstra Australian Championships * 23.16 L 799 P Thomas Barrett 18 ACACI 16/03/2010 2010 Telstra -

Record Revolution Underway Canadian Olympic Trials
CANADIAN OLYMPIC TRIALS RECORD REVOLUTION UNDERWAY $ 4.95 USA NUMBER 258 www.swimnews.com MAY-JUNE 2000 $ 4.95 CAN CANADIANCANADIAN RECORDRECORD SETTERSETTER RICKRICK SAYSAY O'NEILLO'NEILL ANDAND THORPETHORPE RULERULE AUSTRALIANAUSTRALIAN TRIALSTRIALS 2 SWIMNEWS / MAY-JUNE 2000 SWIMNEWS CONTENTS MAY-JUNE 2000 N. J. Thierry, Editor & Publisher CONSECUTIVE NUMBER 258 VOLUME 27, NUMBER 5 Marco Chiesa, Business Manager Karin Helmstaedt, International Editor FEATURES Russ Ewald, Sunland, USA Editor Paul Quinlan, Australian Editor 14 Australian Olympic Trials / Nationals Nick Thierry Cecil Colwin, Ottawa, Features Editor Anita Smale, Copy Editor Aussies Have Strongest Olympic Team in 40 Years Feature Writers George Block, San Antonio, USA 17 Personality: Ian Thorpe Ian Hanson Nikki Dryden, Calgary Knows No Fear, Knows No Barriers or Limits Katharine Dunn, Halifax Wayne Goldsmith, Australia 18 Personality: Susan O’Neill Ian Hanson Anita Lonsbrough, England Oldest Record Falls International Statistical Support Group: Jorge Aguado, Argentina 16-17 Poster: Geoff Huegill Marco Chiesa Rumen Atanasov, Bulgaria Chaker Belhadj, Tunisia 22 Canadian Olympic Trials Katherine Dunn Young-Ryul Cho, Korea Rick Say Betters 20-Year-Old 400 Free Record Szabolcs Fodor, Hungary Gerd Heydn, Germany Three Canadian Records Tumble Franck Jensen, Denmark Berth Johansson, Sweden 23 Qualify for Individual Events and 13 as Relay Alternates Daniel Pichon / Michel Salles, France Hans Peter Sick, Germany 25 Personality: Michael Mintenko Nikki Dryden Juan Antonio Sierra, Spain Neville Smith, South Africa Success at Age 24 Fratisek Stochl, Czech Republic 26 Trends Katherine Dunn Nelson Vargas, Mexico Janusz Wasko, Poland Older, Wiser, and Faster Sumire Watanabe, Japan Computer programs for TAG, World Rankings 27 Nikki’s Diary Nikki Dryden developed by EveryWare Development Corporation. -

MICHAEL KLIM Olympian | Swimming
MICHAEL KLIM Olympian | Swimming One of the most recognisable faces of Australian Swimming. A multiple Olympic gold medalist, World Champion and now a doting family man. A multiple Olympic and World Champion, Michael Klim is part of the star-studded group that has taken Australia back to the top of world swimming. Named Australian Swimming Rookie of the Year in 1995, Klim won a bronze medal at the Atlanta Olympics. His star continued to rise in 1997 when he took the World Record in the 100-metre butterfly on the way to being named World Swimmer of the Year. At the 1998 FINA World Championships in Perth, Klim's record haul of seven medals in seven events including four gold rates as one of the most outstanding performances by an Australian at an international swim meet. The 1998 Commonwealth Games in Kuala Lumpur saw Klim exert his dominance, winning seven medals including four gold once again. Klim was one of the undisputed stars of the Sydney Olympic Games with two gold and two silver. He was instrumental in the Australians' thrilling 4x100m relay victory, unleashing a world record lead off swim to win his first gold on the first night. Klim later helped smash the world record in the 4x200m relay to win his second gold. Back in the pool in 2001 at the FINA World Championships, Klim showed he had not lost his golden touch, winning two gold medals and setting a world record in the 4x200m freestyle relay. An amazing effort for a man who only days earlier had seriously injured his ankle. -

Tomorrow's Swimmer Today Ncaa Championships
NCAA CHAMPIONSHIPS TOMORROW'S SWIMMER TODAY $ 4.95 USA NUMBER 256 www.swimnews.com MARCH 2000 $ 4.95 CAN FIVEFIVE GOLDSGOLDS FORFOR NEILNEIL WALKERWALKER ATAT SCSC WORLDSWORLDS RICKRICK SAYSAY BETTERSBETTERS 200200 FREEFREE RECORDRECORD 2 SWIMNEWS / MARCH 2000 SWIMNEWS CONTENTS MARCH 2000 N. J. Thierry, Editor & Publisher CONSECUTIVE NUMBER 256 VOLUME 27, NUMBER 3 Marco Chiesa, Business Manager Karin Helmstaedt, International Editor FEATURES Russ Ewald, Sunland, USA Editor Paul Quinlan, Australian Editor 13 Speedo Spring Nationals Nikki Dryden Cecil Colwin, Ottawa, Features Editor Anita Smale, Copy Editor West is Best as Centres Dominate Feature Writers George Block, San Antonio, USA Record in 200 Free For Rick Say Nikki Dryden, Calgary Katharine Dunn, Halifax 15 Short Course World Championships Nick Thierry Wayne Goldsmith, Australia Anita Lonsbrough, England Fifteen World Records International Statistical Support Group: Americans Win Most Medals Jorge Aguado, Argentina Rumen Atanasov, Bulgaria 18 Women’s NCAA Championships Mary Wagner Chaker Belhadj, Tunisia Young-Ryul Cho, Korea Georgia Wins Second Team Title Szabolcs Fodor, Hungary Gerd Heydn, Germany Two World Records Set Franck Jensen, Denmark Berth Johansson, Sweden 19 Men’s NCAA Championships Mary Wagner Daniel Pichon / Michel Salles, France Hans Peter Sick, Germany Moses Parts The Waters Juan Antonio Sierra, Spain Neville Smith, South Africa Texas Runs Away With Team Title Fratisek Stochl, Czech Republic Nelson Vargas, Mexico Canadian Records for Riley Janes Janusz Wasko, Poland Sumire Watanabe, Japan 21 Ask Judy Judy Goss Computer programs for TAG, World Rankings developed by EveryWare Development Corporation. Don’t Always Expect It! SWIMNEWS established in 1974 Published ten times yearly (January to October) 28 Taking The Next Step Wayne Goldsmith Contents copyright © No portion of this magazine may be reprinted without permission of the publisher.