DOCSLIB.ORG

2018 Table of Polarizabilities

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
2018 Table of Polarizabilities 2018 Table of Polarizabilities Lit.: P. Schwerdtfeger, J. K. Nagle, “2018 Table of Static Dipole Polarizabilities of the Neutral Elements in the Periodic Table”, Mol. Phys. (2019): https://doi.org/10.1080/00268976.2018.1535143 Last update: November 27, 2018 1 18 1 2 H He 1 2 4.50(0) 13 14 15 16 17 1.38(0) 3 4 5 6 7 8 9 10 2 Li Be B C N O F Ne 164(0) 37.7(1) 20.5(1) 11.3(2) 7.4(2) 5.3(2) 3.74(8) 2.66(0) 11 12 13 14 15 16 17 18 3 Na Mg Al Si P S Cl Ar 163(1) 71.2(4) 3 4 5 6 7 8 9 10 11 12 57.8(1) 37.3(7) 25(1) 19.4(1) 14.6(2) 11.1(0) 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 4 K Ca Sc Ti V Cr Mn Fe Co Ni Cu Zn Ga Ge As Se Br Kr 290(1) 161(4) 97(10) 100(10) 87(10) 83(12) 68(9) 62(4) 55(4) 49(3) 47(1) 38.7(3) 50(3) 40(1) 30(1) 29(1) 21(1) 16.8(0) 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 5 Rb Sr Y Zr Nb Mo Tc Ru Rh Pd Ag Cd In Sn Sb Te I Xe 320(1) 197(1) 162(12) 112(13) 98(8) 87(6) 79(10) 72(10) 66(10) 26.1(1) 55(8) 46(2) 65(4) 53(6) 43(2) 38(4) 32.9(1) 27.3(2) 55 56 71 72 73 74 74 76 77 78 79 80 81 82 83 84 85 86 6 Cs Ba Lu Hf Ta W Re Os Ir Pt Au Hg Tl Pb Bi Po At Rn 401(1) 272(10) 137(7) 103(6) 74(20) 68(15) 62(3) 57(3) 54(7) 48(4) 36(3) 33.9(4) 50(2) 47(3) 48(4) 44(4) 42(4) 35(2) 87 88 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 7 Fr Ra Lr Rf Db Sg Bh Hs Mt Ds Rg Cn Nh Fl Mc Lv Ts Og 318(2) 246(4) 320(20) 112(10) 42(4) 40(4) 38(4) 36(4) 34(3) 32(3) 32(6) 28(2) 29(2) 31(4) 71(20) ? 76(15) 58(6) 119 120 8 Uue Ubn 169(4) 159(10) 57 58 59 60 61 62 63 64 65 66 67 68 69 70 6 La Ce Pr Nd Pm Sm Eu Gd Tb Dy Ho Er Tm Yb 215(20) 205(20) 216(20) 208(20) 200(20) 192(20) 184(20) 158(20) 170(20) 165(15) 156(10) 150(15) 144(15) 139(6) 89 90 91 92 93 94 95 96 97 98 99 100 101 102 7 Ac Th Pa U Np Pu Am Cm Bk Cf Es Fm Md No 203(12) 217(54) 154(20) 129(17) 151(20) 132(20) 131(25) 144(25) 125(25) 122(20) 118(20) 113(20) 109(20) 110(6) Figure 1. Recommended values from Table 1 for the atomic polarizabilities (atomic units; estimated uncertainties in parentheses) of elements Z = 1-120. The various blocks of elements are color-coded: s-block, yellow; p-block, green; d-block, blue; f-block, orange. Acknowledgment PS thanks Ivan Lim, Gordon W. F. Drake (Windsor), Nicola Gaston (Auckland), Uwe Hohm (Braunschweig), Antonio Rizzo (Pisa), Jürgen Hinze (Bielefeld), Gary Doolen (Los Alamos National Laboratory), Dirk Andrae (Bielefeld), Vitaly Kresin (Los Angeles), Timo Fleig (Düsseldorf), Ajit Thakkar (Fredericton), Pekka Pyykkö (Helsinki), Zong-Chao Yan, (Brunswick), Juha Tiihonen (Helsinki) and Keith Bonin (Winston-Salem) for helpful discussions. Financial support from Marsden funding (17-MAU-021) by the Royal Society of New Zealand is gratefully acknowledged. JN thanks Bowdoin College for sabbatical leave support. 2 Table 1. Static scalar dipole polarizabilities (in atomic units) for neutral atoms. If not otherwise indicated by the state symmetry, ML (MJ) - averaged polarizabilities are listed; ML (MJ) respectively denotes that the polarizability for each ML (MJ) state can be found in the reference given. Abbreviations used (uncertainties given here consistently as ± values): exp.: experimentally determined value; NR: nonrelativistic; R: Relativistic, DK: Scalar relativistic Douglas-Kroll; MVD: mass-velocity-Darwin; SO: Spin-orbit coupled; SF: Dyall’s spin-free formalism (scalar relativistic); PP: relativistic pseudopotential; LDA: local (spin) density approximation; PW91: Perdew-Wang 91 functional; RPA: Random phase approximation; PolPot: Polarization potential; MBPT: many-body perturbation theory; CI: configuration interaction; CCSD(T): coupled cluster singles doubles (SD) with perturbative triples; FS Fock-space; CEPA: coupled electron pair approximation; MR: multi- reference; CAS: complete active space; VPA: variational perturbation approach. For all other abbreviations see text or references. If the symmetry of the state is not clearly specified as in Doolen’s calculations, the calculation was most likely set at a specific configuration (orbital occupancy) as listed in the Desclaux tables [1], reflecting the ground state symmetry of the specific atom. NB: 1 a.u. = 0.14818471 Å3 = 1.6487773 ´ 10–41 C m2/V. 3 Z Atom Refs. State aD Comments 1 H [2] 2S 4.5 NR, exact 2 [2,3] S1/2 4.49975149589 R, Dirac, variational, Slater basis/B-splines (more digits are given in ref 3) 2 [4] S1/2 4.49975149518 R, Dirac, Lagrange mesh method (more digits are given in this paper) 2 1 [3] S1/2 4.507107623 R, Dirac (as above), but with finite mass correction added for the H isotope 2 S1/2 4.50711±0.00003 recommended 1 4 2 He [5] S0 1.383191 R, Dirac, Breit-Pauli, QED, mass pol., correlated basis ( He) 1 [6] S0 1.38376079 R, Dirac, Breit-Pauli, QED, mass pol., exponentially correlated Slater ±0.00000023 functions (4He) 1 4 [7] S0 1.3837295330 R, Dirac, Breit, QED, recoil, … ( He) ±0.0000000001 1 [8,9] S0 1.383746±0.000007 exp. 1 [10] S0 1.383759±0.000013 exp. 1 S0 1.38375±0.00002 recommended 3 Li [11,12] 2S 164.05 NR, exponentially correlated Gaussians [18] + R/DK 2 7 [13] S1/2 164.084 R, Dirac, MBPT, Breit, QED, recoil ( Li) 2 7 [14] S1/2 164.1125±0.0005 Hylleraas basis, R(MV+Darwin+Breit), QED, recoil ( Li) 2 [15] S1/2 164.21 Frozen core Hamiltonian, semi-empirical polarization potential 2 [16] S1/2 164.0±3.4 exp. 2 [17] S1/2 164.2±1.1 exp. 2 S1/2 164.1125±0.0005 recommended 4 Z Atom Refs. State aD Comments 4 Be [11] 1S 37.755 NR, exponentially correlated Gaussians [18] 1 [19] S0 37.80±0.47 R, Dirac, coupled cluster 1 [20] S0 37.76±0.22 R, Dirac, CI+MBPT+ experimental data 1 [11,21] S0 37.739±0.030 R correction of –0.016 applied to value from ref [11] 1 [22] S0 37.86±0.17 R, Dirac, MBPT, CCSD 1 [23] S0 37.73±0.05 CCSD(T) 1 [24] S0 37.807 CI, expanded London formula 1 [25] S0 37.69 Combination of ab initio and semi-empirical methods 1 [26] S0 37.29 All-electron SCF plus valence CI 1 [27] S0 37.9 Model potential 37.74±0.03 recommended 2 5 B [28] P 20.47 NR, PNO-CEPA, ML res. 2 [29] P 20.43±0.11 NR, CCSD(T), ML res. 2 [30] P 20.59 R, SF, MRCI, ML res. 2 2 [30] P1/2/ P3/2 20.53/20.54 R, Dirac, MRCI, MJ res. 20.5±0.1 recommended 3 6 C [31] P 11.39 NR, CASPT2, ML res. 3 [29] P 11.67±0.07 NR, CCSD(T), ML res. 3 [32] P0 11.26±0.20 R, Dirac+Gaunt, CCSD(T) 11.3±0.2 recommended 7 N [28] 4S 7.43 NR, PNO-CEPA 4 [33] S 7.41 R, DK, CASPT2 4 [29] S 7.26±0.05 NR, CCSD(T) 4 [16,34] S3/2 7.6±0.4 exp. 4 [35,36] S3/2 7.28 exp. 7.4±0.2 recommended 5 Z Atom Refs. State aD Comments 3 8 O [28,86] P 5.41±0.11 NR, PNO-CEPA, ML res. 3 [31] P 5.4±0.7 NR, CASPT2, ML res. 3 [21,29] P 5.24±0.04 NR, CCSD(T), ML res. 3 [34] P2 5.2±0.4 exp. 5.3±0.2 recommended 2 9 F [28] P 3.76 NR, PNO-CEPA, ML res. 2 [37] P 3.76±0.06 NR, CASPT2, ML res. 2 [29] P 3.70±0.03 NR, CCSD(T), ML res. 3.74±0.08 recommended 10 Ne [38] 1S 2.68 NR, CCSD(T) 1 [39] S 2.665 NR, CC3 1 [39,40,41] S 2.666 R, CC3+FCI+DK3 correction 1 [42,43] S0 2.677±0.070 R, Dirac-Coulomb, non-linear PRCC 1 [44] S0 2.66063±0.00001 CCSD(T), ECP 1 [21] S0 2.661±0.005 R, CCSD(T) 1 [45] S0 2.663 exp. 1 [46] S0 2.6669±0.0008 exp. 1 [47] S0 2.66110±0.00003 exp. 2.66110±0.00003 recommended 2 11 Na [48] S1/2 162.6±0.3 R, SD all orders + exp.
Load more

Recommended publications
  • Appendix 1 Dynamic Polarizability of an Atom
    Appendix 1 Dynamic Polarizability of an Atom Definition of Dynamic Polarizability The dynamic (dipole) polarizability aoðÞis an important spectroscopic characteris- tic of atoms and nanoobjects describing the response to external electromagnetic disturbance in the case that the disturbing field strength is much less than the atomic << 2 5 4 : 9 = electric field strength E Ea ¼ me e h ffi 5 14 Á 10 V cm, and the electromag- netic wave length is much more than the atom size. From the mathematical point of view dynamic polarizability in the general case is the tensor of the second order aij connecting the dipole moment d induced in the electron core of a particle and the strength of the external electric field E (at the frequency o): X diðÞ¼o aijðÞo EjðÞo : (A.1) j For spherically symmetrical systems the polarizability aij is reduced to a scalar: aijðÞ¼o aoðÞdij; (A.2) where dij is the Kronnecker symbol equal to one if the indices have the same values and to zero if not. Then the Eq. A.1 takes the simple form: dðÞ¼o aoðÞEðÞo : (A.3) The polarizability of atoms defines the dielectric permittivity of a medium eoðÞ according to the Clausius-Mossotti equation: eoðÞÀ1 4 ¼ p n aoðÞ; (A.4) eoðÞþ2 3 a V. Astapenko, Polarization Bremsstrahlung on Atoms, Plasmas, Nanostructures 347 and Solids, Springer Series on Atomic, Optical, and Plasma Physics 72, DOI 10.1007/978-3-642-34082-6, # Springer-Verlag Berlin Heidelberg 2013 348 Appendix 1 Dynamic Polarizability of an Atom where na is the concentration of substance atoms.
    [Show full text]
  • Structure and Bonding Electron Configurations in the Periodic Table
    Structure and Bonding The study of organic chemistry must at some point extend to the molecular level, for the physical and chemical properties of a substance are ultimately explained in terms of the structure and bonding of molecules. This module introduces some basic facts and principles that are needed for a discussion of organic molecules. Electronic Configurations Electron Configurations in the Periodic Table 1A 2A 3A 4A 5A 6A 7A 8A 1 2 H He 1 2 1s 1s 3 4 5 6 7 8 9 10 Li Be B C N O F Ne 2 2 2 2 2 2 2 2 1s 1s 1s 1s 1s 1s 1s 1s 2s1 2s2 2s22p1 2s22p2 2s22p3 2s22p4 2s22p5 2s22p6 11 12 13 14 15 16 17 18 Na Mg Al Si P S Cl Ar [Ne] [Ne] [Ne] [Ne] [Ne] [Ne] [Ne] [Ne] 3s1 3s2 3s23p1 3s23p2 3s23p3 3s23p4 3s23p5 3s23p6 Four elements, hydrogen, carbon, oxygen and nitrogen, are the major components of most organic compounds. Consequently, our understanding of organic chemistry must have, as a foundation, an appreciation of the electronic structure and properties of these elements. The truncated periodic table shown above provides the orbital electronic structure for the first eighteen elements (hydrogen through argon). According to the Aufbau principle, the electrons of an atom occupy quantum levels or orbitals starting from the lowest energy level, and proceeding to the highest, with each orbital holding a maximum of two paired electrons (opposite spins). Electron shell #1 has the lowest energy and its s-orbital is the first to be filled.
    [Show full text]
  • VSEPR Theory
    VSEPR Theory The valence-shell electron-pair repulsion (VSEPR) model is often used in chemistry to predict the three dimensional arrangement, or the geometry, of molecules. This model predicts the shape of a molecule by taking into account the repulsion between electron pairs. This handout will discuss how to use the VSEPR model to predict electron and molecular geometry. Here are some definitions for terms that will be used throughout this handout: Electron Domain – The region in which electrons are most likely to be found (bonding and nonbonding). A lone pair, single, double, or triple bond represents one region of an electron domain. H2O has four domains: 2 single bonds and 2 nonbonding lone pairs. Electron Domain may also be referred to as the steric number. Nonbonding Pairs Bonding Pairs Electron domain geometry - The arrangement of electron domains surrounding the central atom of a molecule or ion. Molecular geometry - The arrangement of the atoms in a molecule (The nonbonding domains are not included in the description). Bond angles (BA) - The angle between two adjacent bonds in the same atom. The bond angles are affected by all electron domains, but they only describe the angle between bonding electrons. Lewis structure - A 2-dimensional drawing that shows the bonding of a molecule’s atoms as well as lone pairs of electrons that may exist in the molecule. Provided by VSEPR Theory The Academic Center for Excellence 1 April 2019 Octet Rule – Atoms will gain, lose, or share electrons to have a full outer shell consisting of 8 electrons. When drawing Lewis structures or molecules, each atom should have an octet.
    [Show full text]
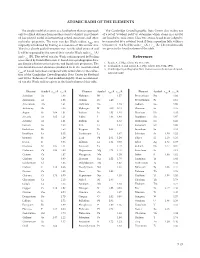
  • ATOMIC RADII of the ELEMENTS References
    ATOMIC RADII OF THE ElEMENTS The simple model of an atom as a hard sphere that can approach The Cambridge Crystallographic Data Center also makes use only to a fixed distance from another atom to which it is not bond- of a set of “covalent radii” to determine which atoms in a crystal ed has proved useful in interpreting crystal structures and other are bonded to each other . Thus two atoms A and B are judged to molecular properties . The term van der Waals radius, rvdw, was be connected by a covalent bond if their separation falls within a originally introduced by Pauling as a measure of this atomic size . tolerance of ±0 .4 Å of the sum rcov (A) + rcov (B) . The covalent radii Thus in a closely packed structure two non-bonded atoms A and are given in the fourth column of the table . B will be separated by the sum of their van der Waals radii rvdw (A) and rvdw (B) . The set of van der Waals radii proposed by Pauling References was refined by Bondi (Reference 1) based on crystallographic data, gas kinetic collision cross sections, and liquid state properties . The 1 . Bondi, A ., J. Phys. Chem. 68, 441, 1964 . non-bonded contact distances predicted from the recommended 2 . Rowland, R . S . and Taylor, R ., J. Phys. Chem. 100, 7384, 1996 . 3 . Cambridge Crystallographic Data Center, www .ccdc .cam .ac .uk/prod- r of Bondi have been compared with actual data in the collec- vdw ucts/csd/radii/ tion of the Cambridge Crystallographic Data Center by Rowland and Taylor (Reference 2) and modified slightly .
    [Show full text]
  • 8.3 Bonding Theories >
    8.3 Bonding Theories > Chapter 8 Covalent Bonding 8.1 Molecular Compounds 8.2 The Nature of Covalent Bonding 8.3 Bonding Theories 8.4 Polar Bonds and Molecules 1 Copyright © Pearson Education, Inc., or its affiliates. All Rights Reserved. 8.3 Bonding Theories > Molecular Orbitals Molecular Orbitals How are atomic and molecular orbitals related? 2 Copyright © Pearson Education, Inc., or its affiliates. All Rights Reserved. 8.3 Bonding Theories > Molecular Orbitals • The model you have been using for covalent bonding assumes the orbitals are those of the individual atoms. • There is a quantum mechanical model of bonding, however, that describes the electrons in molecules using orbitals that exist only for groupings of atoms. 3 Copyright © Pearson Education, Inc., or its affiliates. All Rights Reserved. 8.3 Bonding Theories > Molecular Orbitals • When two atoms combine, this model assumes that their atomic orbitals overlap to produce molecular orbitals, or orbitals that apply to the entire molecule. 4 Copyright © Pearson Education, Inc., or its affiliates. All Rights Reserved. 8.3 Bonding Theories > Molecular Orbitals Just as an atomic orbital belongs to a particular atom, a molecular orbital belongs to a molecule as a whole. • A molecular orbital that can be occupied by two electrons of a covalent bond is called a bonding orbital. 5 Copyright © Pearson Education, Inc., or its affiliates. All Rights Reserved. 8.3 Bonding Theories > Molecular Orbitals Sigma Bonds When two atomic orbitals combine to form a molecular orbital that is symmetrical around the axis connecting two atomic nuclei, a sigma bond is formed. • Its symbol is the Greek letter sigma (σ).
    [Show full text]
  • Chemical Bonding & Chemical Structure
    Chemistry 201 – 2009 Chapter 1, Page 1 Chapter 1 – Chemical Bonding & Chemical Structure ings from inside your textbook because I normally ex- Getting Started pect you to read the entire chapter. 4. Finally, there will often be a Supplement that con- If you’ve downloaded this guide, it means you’re getting tains comments on material that I have found espe- serious about studying. So do you already have an idea cially tricky. Material that I expect you to memorize about how you’re going to study? will also be placed here. Maybe you thought you would read all of chapter 1 and then try the homework? That sounds good. Or maybe you Checklist thought you’d read a little bit, then do some problems from the book, and just keep switching back and forth? That When you have finished studying Chapter 1, you should be sounds really good. Or … maybe you thought you would able to:1 go through the chapter and make a list of all of the impor- tant technical terms in bold? That might be good too. 1. State the number of valence electrons on the following atoms: H, Li, Na, K, Mg, B, Al, C, Si, N, P, O, S, F, So what point am I trying to make here? Simply this – you Cl, Br, I should do whatever you think will work. Try something. Do something. Anything you do will help. 2. Draw and interpret Lewis structures Are some things better to do than others? Of course! But a. Use bond lengths to predict bond orders, and vice figuring out which study methods work well and which versa ones don’t will take time.
    [Show full text]
  • Atomic and Ionic Radii of Elements 1–96 Martinrahm,*[A] Roald Hoffmann,*[A] and N
    DOI:10.1002/chem.201602949 Full Paper & Elemental Radii Atomic and Ionic Radii of Elements 1–96 MartinRahm,*[a] Roald Hoffmann,*[a] and N. W. Ashcroft[b] Abstract: Atomic and cationic radii have been calculated for tive measureofthe sizes of non-interacting atoms, common- the first 96 elements, together with selected anionicradii. ly invoked in the rationalization of chemicalbonding, struc- The metric adopted is the average distance from the nucleus ture, and different properties. Remarkably,the atomic radii where the electron density falls to 0.001 electrons per bohr3, as defined in this way correlate well with van der Waals radii following earlier work by Boyd. Our radii are derived using derived from crystal structures. Arationalizationfor trends relativistic all-electron density functional theory calculations, and exceptionsinthose correlations is provided. close to the basis set limit. They offer asystematic quantita- Introduction cule,[2] but we prefer to follow through with aconsistent pic- ture, one of gauging the density in the atomic groundstate. What is the size of an atom or an ion?This question has been The attractivenessofdefining radii from the electron density anatural one to ask over the centurythat we have had good is that a) the electron density is, at least in principle, an experi- experimental metricinformation on atoms in every form of mental observable,and b) it is the electron density at the out- matter,and (more recently) reliable theory for thesesame ermost regionsofasystem that determines Pauli/exchange/ atoms. And the momentone asks this question one knows same-spinrepulsions, or attractive bondinginteractions, with that there is no unique answer.Anatom or ion coursing down achemical surrounding.
    [Show full text]
  • ARC: an Open-Source Library for Calculating Properties of Alkali Rydberg Atoms
    ARC: An open-source library for calculating properties of alkali Rydberg atoms N. Šibalic´a,∗, J. D. Pritchardb, C. S. Adamsa, K. J. Weatherilla aJoint Quantum Center (JQC) Durham-Newcastle, Department of Physics, Durham University, South Road, Durham, DH1 3LE, United Kingdom bDepartment of Physics, SUPA, University of Strathclyde, 107 Rottenrow East, Glasgow, G4 0NG, United Kingdom Abstract We present an object-oriented Python library for computation of properties of highly-excited Rydberg states of alkali atoms. These include single-body effects such as dipole matrix elements, excited-state lifetimes (radiative and black-body limited) and Stark maps of atoms in external electric fields, as well as two-atom interaction potentials accounting for dipole and quadrupole coupling effects valid at both long and short range for arbitrary placement of the atomic dipoles. The package is cross-referenced to precise measurements of atomic energy levels and features extensive documentation to facilitate rapid upgrade or expansion by users. This library has direct application in the field of quantum information and quantum optics which exploit the strong Rydberg dipolar interactions for two-qubit gates, robust atom-light interfaces and simulating quantum many-body physics, as well as the field of metrology using Rydberg atoms as precise microwave electrometers. Keywords: Alkali atom, Matrix elements, Dipole-dipole interactions, Stark shift, Förster resonances PROGRAM SUMMARY They are a flourishing field for quantum information process- Program Title: ARC: Alkali Rydberg Calculator ing [1, 2] and quantum optics [3, 4, 5] in the few to single exci- Licensing provisions: BSD-3-Clause tation regime, as well as many-body physics [6, 7, 8, 9, 10, 11], Programming language: Python 2.7 or 3.5, with C extension in the many-excitations limit.
    [Show full text]
  • Electron Configurations, Orbital Notation and Quantum Numbers
    5 Electron Configurations, Orbital Notation and Quantum Numbers Electron Configurations, Orbital Notation and Quantum Numbers Understanding Electron Arrangement and Oxidation States Chemical properties depend on the number and arrangement of electrons in an atom. Usually, only the valence or outermost electrons are involved in chemical reactions. The electron cloud is compartmentalized. We model this compartmentalization through the use of electron configurations and orbital notations. The compartmentalization is as follows, energy levels have sublevels which have orbitals within them. We can use an apartment building as an analogy. The atom is the building, the floors of the apartment building are the energy levels, the apartments on a given floor are the orbitals and electrons reside inside the orbitals. There are two governing rules to consider when assigning electron configurations and orbital notations. Along with these rules, you must remember electrons are lazy and they hate each other, they will fill the lowest energy states first AND electrons repel each other since like charges repel. Rule 1: The Pauli Exclusion Principle In 1925, Wolfgang Pauli stated: No two electrons in an atom can have the same set of four quantum numbers. This means no atomic orbital can contain more than TWO electrons and the electrons must be of opposite spin if they are to form a pair within an orbital. Rule 2: Hunds Rule The most stable arrangement of electrons is one with the maximum number of unpaired electrons. It minimizes electron-electron repulsions and stabilizes the atom. Here is an analogy. In large families with several children, it is a luxury for each child to have their own room.
    [Show full text]
  • Atomic Structure and Bonding
    IM2665 Chemistry of Nanomaterials Atomic Structure and Bonding Assoc. Prof. Muhammet Toprak Division of Functional Materials KTH Royal Institute of Technology Background • Electromagnetic waves • Materials wave motion, • Quantified energy and – Louis de Broglie (1892-1987) photons • Uncertainity principle – Max Planck (1858-1947) – Werner Heisenberg (1901-1976) – Albert Einstein (1879-1955) • Schrödinger equation • Bohr’s atom model – Erwin Schrödinger (1887-1961) – Niels Bohr (1885-1962) IM2657 Nanostr. Mater. & Self Assembly 2 Electromagnetic Spectrum Visible light is only a small part of the Electromagnetic Spectrum IM2657 Nanostr. Mater. & Self Assembly 3 Electromagnetic Waves • Wavemotion is defined by • Calculations – ν = Frequency ( Hz) – c = ν × λ – λ = wavelength (m) – c = 3,00 × 108 m/s (speed of light) IM2657 Nanostr. Mater. & Self Assembly 4 Quantified Energy and Photons • E = h × ν; where h = 6,63 × 10-34 J s (Planck’s constant) • Photoelectric Effect (1905) IM2657 Nanostr. Mater. & Self Assembly 5 Thomson´s Pudding Model For a helium atom, the model proposes a large spherical cloud with two units of positive charge. Th e two electrons lie on a line through the center of the cloud. The loss of one electron produces the He+1 ion, with the remaining electron at the center of the cloud. The loss of a second electron prod uces He+2 , in which there is just a cloud of positive charge. IM2657 Nanostr. Mater. & Self Assembly 6 Rutherford’s Experiment The notion that atoms consist of very small nuclei containing protons and neutrons surrounded by a much larger cloud of electrons was IM2657 Nanostr. Mater. & Self Assembly 7 developed from an α particle scattering experiment.
    [Show full text]
  • Coupled Electricity and Magnetism: Multiferroics and Beyond
    Coupled electricity and magnetism: multiferroics and beyond Daniel Khomskii Cologne University, Germany JMMM 306, 1 (2006) Physics (Trends) 2, 20 (2009) Degrees of freedom charge Charge ordering Ferroelectricity Qαβ ρ(r) (monopole) P or D (dipole) (quadrupole) Spin Orbital ordering Magnetic ordering Lattice Maxwell's equations Magnetoelectric effect In Cr2O3 inversion is broken --- it is linear magnetoelectric In Fe2O3 – inversion is not broken, it is not ME (but it has weak ferromagnetism) Magnetoelectric coefficient αij can have both symmetric and antisymmetric parts Pi = αij Hi ; Symmetric: Then along main axes P║H , M║E For antisymmetric tensor αij one can introduce a dual vector T is the toroidal moment (both P and T-odd). Then P ┴ H, M ┴ E, P = [T x H], M = - [T x E] For localized spins For example, toroidal moment exists in magnetic vortex Coupling of electric polarization to magnetism Time reversal symmetry P → +P t → −t M → −M Inversion symmetry E ∝ αHE P → −P r → −r M → +M MULTIFERROICS Materials combining ferroelectricity, (ferro)magnetism and (ferro)elasticity If successful – a lot of possible applications (e.g. electrically controlling magnetic memory, etc) Field active in 60-th – 70-th, mostly in the Soviet Union Revival of the interest starting from ~2000 • Perovskites: either – or; why? • The ways out: Type-I multiferroics: Independent FE and magnetic subsystems 1) “Mixed” systems 2) Lone pairs 3) “Geometric” FE 4) FE due to charge ordering Type-II multiferroics:FE due to magnetic ordering 1) Magnetic spirals (spin-orbit interaction) 2) Exchange striction mechanism 3) Electronic mechanism Two general sets of problems: Phenomenological treatment of coupling of M and P; symmetry requirements, etc.
    [Show full text]
  • Density Functional Studies of the Dipole Polarizabilities of Substituted Stilbene, Azoarene and Related Push-Pull Molecules
    Int. J. Mol. Sci. 2004, 5, 224-238 International Journal of Molecular Sciences ISSN 1422-0067 © 2004 by MDPI www.mdpi.org/ijms/ Density Functional Studies of the Dipole Polarizabilities of Substituted Stilbene, Azoarene and Related Push-Pull Molecules Alan Hinchliffe 1,*, Beatrice Nikolaidi 1 and Humberto J. Soscún Machado 2 1 The University of Manchester, School of Chemistry (North Campus), Sackville Street, Manchester M60 1QD, UK. 2 Departamento de Química, Fac. Exp. de Ciencias, La Universidad del Zulia, Grano de Oro Módulo No. 2, Maracaibo, Venezuela. * Corresponding author; E-mail: [email protected] Received: 3 June 2004; in revised form: 15 August 2004 / Accepted: 16 August 2004 / Published: 30 September 2004 Abstract: We report high quality B3LYP Ab Initio studies of the electric dipole polarizability of three related series of molecules: para-XC6H4Y, XC6H4CH=CHC6H4Y and XC6H4N=NC6H4Y, where X and Y represent H together with the six various activating through deactivating groups NH2, OH, OCH3, CHO, CN and NO2. Molecules for which X is activating and Y deactivating all show an enhancement to the mean polarizability compared to the unsubstituted molecule, in accord with the order given above. A number of representative Ab Initio calculations at different levels of theory are discussed for azoarene; all subsequent Ab Initio polarizability calculations were done at the B3LYP/6-311G(2d,1p)//B3LYP/6-311++G(2d,1p) level of theory. We also consider semi-empirical polarizability and molecular volume calculations at the AM1 level of theory together with QSAR-quality empirical polarizability calculations using Miller’s scheme. Least-squares correlations between the various sets of results show that these less costly procedures are reliable predictors of <α> for the first series of molecules, but less reliable for the larger molecules.
    [Show full text]