Alternative Logics and Applied Mathematics [Draft of 5 March 2018]
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

A Simple Logic for Comparisons and Vagueness
THEODORE J. EVERETT A SIMPLE LOGIC FOR COMPARISONS AND VAGUENESS ABSTRACT. I provide an intuitive, semantic account of a new logic for comparisons (CL), in which atomic statements are assigned both a classical truth-value and a “how much” value or extension in the range [0, 1]. The truth-value of each comparison is determined by the extensions of its component sentences; the truth-value of each atomic depends on whether its extension matches a separate standard for its predicate; everything else is computed classically. CL is less radical than Casari’s comparative logics, in that it does not allow for the formation of comparative statements out of truth-functional molecules. I argue that CL provides a better analysis of comparisons and predicate vagueness than classical logic, fuzzy logic or supervaluation theory. CL provides a model for descriptions of the world in terms of comparisons only. The sorites paradox can be solved by the elimination of atomic sentences. In his recent book on vagueness, Timothy Williamson (1994) attacks accounts of vagueness arising from either fuzzy logic or supervaluation theory, both of which have well-known problems, stemming in part from their denial of classical bivalence. He then gives his own, epistemic ac- count of vagueness, according to which the vagueness of a predicate is fundamentally a matter of our not knowing whether or not it applies in every case. My main purpose in this paper is not to criticize William- son’s positive view, but to provide an alternative, non-epistemic account of predicate vagueness, based on a very simple logic for comparisons (CL), which preserves bivalence. -

Does Informal Logic Have Anything to Learn from Fuzzy Logic?
University of Windsor Scholarship at UWindsor OSSA Conference Archive OSSA 3 May 15th, 9:00 AM - May 17th, 5:00 PM Does informal logic have anything to learn from fuzzy logic? John Woods University of British Columbia Follow this and additional works at: https://scholar.uwindsor.ca/ossaarchive Part of the Philosophy Commons Woods, John, "Does informal logic have anything to learn from fuzzy logic?" (1999). OSSA Conference Archive. 62. https://scholar.uwindsor.ca/ossaarchive/OSSA3/papersandcommentaries/62 This Paper is brought to you for free and open access by the Conferences and Conference Proceedings at Scholarship at UWindsor. It has been accepted for inclusion in OSSA Conference Archive by an authorized conference organizer of Scholarship at UWindsor. For more information, please contact [email protected]. Title: Does informal logic have anything to learn from fuzzy logic? Author: John Woods Response to this paper by: Rolf George (c)2000 John Woods 1. Motivation Since antiquity, philosophers have been challenged by the apparent vagueness of everyday thought and experience. How, these philosophers have wanted to know, are the things we say and think compatible with logical laws such as Excluded Middle?1 A kindred attraction has been the question of how truth presents itself — relatively and in degrees? in approximations? in resemblances, or in bits and pieces? F.H. Bradley is a celebrated (or as the case may be, excoriated) champion of the degrees view of truth. There are, one may say, two main views of error, the absolute and relative. According to the former view there are perfect truths, and on the other side there are sheer errors.. -

Section 1.4: Predicate Logic
Section 1.4: Predicate Logic January 22, 2021 Abstract We now consider the logic associated with predicate wffs, including a new set of derivation rules for demonstrating validity (the analogue of tautology in the propositional calculus) – that is, for proving theorems! 1 Derivation rules • First of all, all the rules of propositional logic still hold. Whew! Propositional wffs are simply boring, variable-less predicate wffs. • Our author suggests the following “general plan of attack”: – strip off the quantifiers – work with the separate wffs – insert quantifiers as necessary Now, how may we legitimately do so? Consider the classic syllo- gism: a. (All) Humans are mortal. b. Socrates is human. Therefore Socrates is mortal. The way we reason is that the rule “Humans are mortal” applies to the specific example “Socrates”; hence this Socrates is mortal. We might write this as a. (∀x)(H(x) → M(x)) b. H(s) Therefore M(s). It seems so obvious! But how do we justify that in a proof se- quence? • New rules for predicate logic: in the following, you should un- derstand by the symbol x in P (x) an expression with free variable x, possibly containing other (quantified) variables: e.g. P (x) ≡ (∀y)(∃z)Q(x,y,z) (1) – Universal Instantiation: from (∀x)P (x) deduce P (t). Caveat: t must not already appear as a variable in the ex- pression for P (x): in the equation above, (1), it would not do to deduce P (y) or P (z), as those variables appear in the expression (in a quantified fashion) already. -

Pure Mathematics Professors Teaching and Leading Research CO-OP OR REGULAR 28
PURE MATHEMATICS Pure Mathematics professors teaching and leading research CO-OP OR REGULAR 28 Mathematician ranked among top 10 TOP 10 jobs from 2011-2017 – Comcast.com of grads are employed Search for a deeper 96.6% within 2 years understanding of mathematics Pure mathematics is at the foundation of all mathematical reasoning. If first-year calculus ALEX teaches you how to drive the car, Pure Mathematics teaches you how to build one. 3B, PURE MATHEMATICS AND Mathematicians know that there could be no general relativity without differential COMBINATORICS AND geometry, and no computer security without advanced number theory. OPTIMIZATION Pure Mathematics at Waterloo is a small, cohesive, and challenging program that will open countless doors for you. Our graduates have used the program as a springboard into careers WHAT DO YOU LOVE ABOUT in information technology, finance, business, science, education, and insurance, often by way PURE MATHEMATICS? The satisfaction from understanding of some of the most prestigious graduate programs in the world. an idea at a deeper level and tying together unrelated branches of ALEX’S FAVOURITE COURSES mathematics or physics for the › PMATH 320 Euclidean Geometry: This course is everything you love about Geometry: first time is the most rewarding Euclid’s axioms, isometries of the Euclidean plane and of Euclidean space, polygons, part of learning and understanding polyhedral, polytopes, and the kissing problem. mathematics. What I really enjoy is › PMATH 351 Real Analysis: It’s a very intuitive and natural approach to real analysis, and the developing a deep understanding of complexity of the course builds very naturally to the end of the semester. -

Intransitivity and Vagueness
Intransitivity and Vagueness Joseph Y. Halpern∗ Cornell University Computer Science Department Ithaca, NY 14853 [email protected] http://www.cs.cornell.edu/home/halpern Abstract preferences. Moreover, it is this intuition that forms the ba- sis of the partitional model for knowledge used in game the- There are many examples in the literature that suggest that indistinguishability is intransitive, despite the fact that the in- ory (see, e.g., [Aumann 1976]) and in the distributed sys- distinguishability relation is typically taken to be an equiv- tems community [Fagin, Halpern, Moses, and Vardi 1995]. alence relation (and thus transitive). It is shown that if the On the other hand, besides the obvious experimental obser- uncertainty perception and the question of when an agent vations, there have been arguments going back to at least reports that two things are indistinguishable are both care- Poincare´ [1902] that the physical world is not transitive in fully modeled, the problems disappear, and indistinguishabil- this sense. In this paper, I try to reconcile our intuitions ity can indeed be taken to be an equivalence relation. More- about indistinguishability with the experimental observa- over, this model also suggests a logic of vagueness that seems tions, in a way that seems (at least to me) both intuitively to solve many of the problems related to vagueness discussed appealing and psychologically plausible. I then go on to ap- in the philosophical literature. In particular, it is shown here ply the ideas developed to the problem of vagueness. how the logic can handle the Sorites Paradox. To understand the vagueness problem, consider the well- n+1 1 Introduction known Sorites Paradox: If grains of sand make a heap, then so do n. -

On the Relationship Between Fuzzy Autoepistemic Logic and Fuzzy Modal Logics of Belief
JID:FSS AID:6759 /FLA [m3SC+; v1.204; Prn:31/03/2015; 9:42] P.1(1-26) Available online at www.sciencedirect.com ScienceDirect Fuzzy Sets and Systems ••• (••••) •••–••• www.elsevier.com/locate/fss On the relationship between fuzzy autoepistemic logic and fuzzy modal logics of belief ∗ Marjon Blondeel d, ,1, Tommaso Flaminio a,2, Steven Schockaert b, Lluís Godo c,3, Martine De Cock d,e a Università dell’Insubria, Department of Theorical and Applied Science, Via Mazzini 5, 21100 Varese, Italy b Cardiff University, School of Computer Science and Informatics, 5The Parade, Cardiff, CF24 3AA, UK c Artficial Intelligence Research Institute (IIIA) – CSIC, Campus UAB, 08193 Bellaterra, Spain d Ghent University, Department of Applied Mathematics, Computer Science and Statistics, Krijgslaan 281 (S9), 9000 Gent, Belgium e University of Washington Tacoma – Center for Web and Data Science, 1900 Commerce Street, Tacoma, WA 98402-3100, USA Received 12 February 2014; received in revised form 30 September 2014; accepted 26 February 2015 Abstract Autoepistemic logic is an important formalism for nonmonotonic reasoning originally intended to model an ideal rational agent reflecting upon his own beliefs. Fuzzy autoepistemic logic is a generalization of autoepistemic logic that allows to represent an agent’s rational beliefs on gradable propositions. It has recently been shown that, in the same way as autoepistemic logic generalizes answer set programming, fuzzy autoepistemic logic generalizes fuzzy answer set programming as well. Besides being related to answer set programming, autoepistemic logic is also closely related to several modal logics. To investigate whether a similar relationship holds in a fuzzy logical setting, we firstly generalize the main modal logics for belief to the setting of finitely-valued c Łukasiewicz logic with truth constants Łk, and secondly we relate them with fuzzy autoepistemic logics. -

Pure Mathematics
Why Study Mathematics? Mathematics reveals hidden patterns that help us understand the world around us. Now much more than arithmetic and geometry, mathematics today is a diverse discipline that deals with data, measurements, and observations from science; with inference, deduction, and proof; and with mathematical models of natural phenomena, of human behavior, and social systems. The process of "doing" mathematics is far more than just calculation or deduction; it involves observation of patterns, testing of conjectures, and estimation of results. As a practical matter, mathematics is a science of pattern and order. Its domain is not molecules or cells, but numbers, chance, form, algorithms, and change. As a science of abstract objects, mathematics relies on logic rather than on observation as its standard of truth, yet employs observation, simulation, and even experimentation as means of discovering truth. The special role of mathematics in education is a consequence of its universal applicability. The results of mathematics--theorems and theories--are both significant and useful; the best results are also elegant and deep. Through its theorems, mathematics offers science both a foundation of truth and a standard of certainty. In addition to theorems and theories, mathematics offers distinctive modes of thought which are both versatile and powerful, including modeling, abstraction, optimization, logical analysis, inference from data, and use of symbols. Mathematics, as a major intellectual tradition, is a subject appreciated as much for its beauty as for its power. The enduring qualities of such abstract concepts as symmetry, proof, and change have been developed through 3,000 years of intellectual effort. Like language, religion, and music, mathematics is a universal part of human culture. -

Logic and Proof
CS2209A 2017 Applied Logic for Computer Science Lecture 11, 12 Logic and Proof Instructor: Yu Zhen Xie 1 Proofs • What is a theorem? – Lemma, claim, etc • What is a proof? – Where do we start? – Where do we stop? – What steps do we take? – How much detail is needed? 2 The truth 3 Theories and theorems • Theory: axioms + everything derived from them using rules of inference – Euclidean geometry, set theory, theory of reals, theory of integers, Boolean algebra… – In verification: theory of arrays. • Theorem: a true statement in a theory – Proved from axioms (usually, from already proven theorems) Pythagorean theorem • A statement can be a theorem in one theory and false in another! – Between any two numbers there is another number. • A theorem for real numbers. False for integers! 4 Axioms example: Euclid’s postulates I. Through 2 points a line segment can be drawn II. A line segment can be extended to a straight line indefinitely III. Given a line segment, a circle can be drawn with it as a radius and one endpoint as a centre IV. All right angles are congruent V. Parallel postulate 5 Some axioms for propositional logic • For any formulas A, B, C: – A ∨ ¬ – . – . – A • Also, like in arithmetic (with as +, as *) – , – Same holds for ∧. – Also, • And unlike arithmetic – ( ) 6 Counterexamples • To disprove a statement, enough to give a counterexample: a scenario where it is false – To disprove that • Take = ", = #, • Then is false, but B is true. – To disprove that if %& '( ) &, ( , then '( %& ) &, ( , • Set the domain of x and y to be {0,1} • Set P(0,0) and P(1,1) to true, and P(0,1), P(1,0) to false. -

Philosophy 109, Modern Logic Russell Marcus
Philosophy 240: Symbolic Logic Hamilton College Fall 2014 Russell Marcus Reference Sheeet for What Follows Names of Languages PL: Propositional Logic M: Monadic (First-Order) Predicate Logic F: Full (First-Order) Predicate Logic FF: Full (First-Order) Predicate Logic with functors S: Second-Order Predicate Logic Basic Truth Tables - á á @ â á w â á e â á / â 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 0 0 1 1 0 1 0 0 1 0 0 0 0 1 0 1 1 0 1 1 0 0 1 0 0 0 0 0 0 0 1 0 0 1 0 Rules of Inference Modus Ponens (MP) Conjunction (Conj) á e â á á / â â / á A â Modus Tollens (MT) Addition (Add) á e â á / á w â -â / -á Simplification (Simp) Disjunctive Syllogism (DS) á A â / á á w â -á / â Constructive Dilemma (CD) (á e â) Hypothetical Syllogism (HS) (ã e ä) á e â á w ã / â w ä â e ã / á e ã Philosophy 240: Symbolic Logic, Prof. Marcus; Reference Sheet for What Follows, page 2 Rules of Equivalence DeMorgan’s Laws (DM) Contraposition (Cont) -(á A â) W -á w -â á e â W -â e -á -(á w â) W -á A -â Material Implication (Impl) Association (Assoc) á e â W -á w â á w (â w ã) W (á w â) w ã á A (â A ã) W (á A â) A ã Material Equivalence (Equiv) á / â W (á e â) A (â e á) Distribution (Dist) á / â W (á A â) w (-á A -â) á A (â w ã) W (á A â) w (á A ã) á w (â A ã) W (á w â) A (á w ã) Exportation (Exp) á e (â e ã) W (á A â) e ã Commutativity (Com) á w â W â w á Tautology (Taut) á A â W â A á á W á A á á W á w á Double Negation (DN) á W --á Six Derived Rules for the Biconditional Rules of Inference Rules of Equivalence Biconditional Modus Ponens (BMP) Biconditional DeMorgan’s Law (BDM) á / â -(á / â) W -á / â á / â Biconditional Modus Tollens (BMT) Biconditional Commutativity (BCom) á / â á / â W â / á -á / -â Biconditional Hypothetical Syllogism (BHS) Biconditional Contraposition (BCont) á / â á / â W -á / -â â / ã / á / ã Philosophy 240: Symbolic Logic, Prof. -
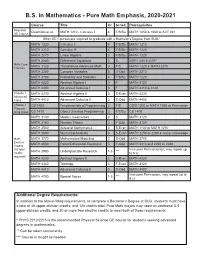
B.S. in Mathematics - Pure Math Emphasis, 2020-2021
B.S. in Mathematics - Pure Math Emphasis, 2020-2021 Course Title Cr. Sched. Prerequisites Required Quantitative Lit. MATH 1210 - Calculus I 4 F/S/Su MATH 1050 & 1060 or ACT 26+ GE Course Other GE Courses are required to graduate with a Bachelor’s Degree from SUU.* MATH 1220 Calculus II 4 F/S/Su MATH 1210 MATH 2210 Calculus III 4 F/S/Su MATH 1220 MATH 2270 Linear Algebra 3 F/S/Su MATH 1220 MATH 2280 Differential Equations 3 S MATH 1220 & 2270** Math Core MATH 3120 Transition to Advanced Math 3 F/S MATH 1220 & MATH 2270 Courses MATH 3250 Complex Variables 3 S-Odd MATH 2210 MATH 3700 Probability and Statistics 4 F/S/Su MATH 1220 MATH 4220 Abstract Algebra I 3 F MATH 3120 MATH 4400 Advanced Calculus I 3 F MATH 2210 & 3120 Choose 1 MATH 4230 Abstract Algebra II 3 S-Even MATH 4220 Advanced Class MATH 4410 Advanced Calculus II 3 S-Odd MATH 4400 Choose 1 CS 1400 Fundamentals of Programming 3 F/S CSIS 1030 or MATH 1050 or Permission Program- ming Class CS 1410 Object Oriented Programming 3 F/S/Su CS 1400 MATH 3130 Modern Geometries 3 S MATH 3120 MATH 3160 Number Theory 3 F-Odd MATH 3120 MATH 3500 Actuarial Mathematics 3 S-Even MATH 1100 or MATH 1210 MATH 3600 Numerical Analysis 3 S-Even MATH 2250 or 2280 & comp. knowledge Math MATH 3770 Mathematical Modeling 3 S-Odd MATH 3700 Elective MATH 3800 Partial Differential Equations 3 F-Odd MATH 2210 and 2250 or 2280 Credits (15 total Instructor Permissission; may repeat up MATH 3990 Undergraduate Research 1-3 *** credits to 5 cr. -

Predicate Logic
Predicate Logic Andreas Klappenecker Predicates A function P from a set D to the set Prop of propositions is called a predicate. The set D is called the domain of P. Example Let D=Z be the set of integers. Let a predicate P: Z -> Prop be given by P(x) = x>3. The predicate itself is neither true or false. However, for any given integer the predicate evaluates to a truth value. For example, P(4) is true and P(2) is false Universal Quantifier (1) Let P be a predicate with domain D. The statement “P(x) holds for all x in D” can be written shortly as ∀xP(x). Universal Quantifier (2) Suppose that P(x) is a predicate over a finite domain, say D={1,2,3}. Then ∀xP(x) is equivalent to P(1)⋀P(2)⋀P(3). Universal Quantifier (3) Let P be a predicate with domain D. ∀xP(x) is true if and only if P(x) is true for all x in D. Put differently, ∀xP(x) is false if and only if P(x) is false for some x in D. Existential Quantifier The statement P(x) holds for some x in the domain D can be written as ∃x P(x) Example: ∃x (x>0 ⋀ x2 = 2) is true if the domain is the real numbers but false if the domain is the rational numbers. Logical Equivalence (1) Two statements involving quantifiers and predicates are logically equivalent if and only if they have the same truth values no matter which predicates are substituted into these statements and which domain is used. -

Chapter 4, Propositional Calculus
ECS 20 Chapter 4, Logic using Propositional Calculus 0. Introduction to Discrete Mathematics. 0.1. Discrete = Individually separate and distinct as opposed to continuous and capable of infinitesimal change. Integers vs. real numbers, or digital sound vs. analog sound. 0.2. Discrete structures include sets, permutations, graphs, trees, variables in computer programs, and finite-state machines. 0.3. Five themes: logic and proofs, discrete structures, combinatorial analysis, induction and recursion, algorithmic thinking, and applications and modeling. 1. Introduction to Logic using Propositional Calculus and Proof 1.1. “Logic” is “the study of the principles of reasoning, especially of the structure of propositions as distinguished from their content and of method and validity in deductive reasoning.” (thefreedictionary.com) 2. Propositions and Compound Propositions 2.1. Proposition (or statement) = a declarative statement (in contrast to a command, a question, or an exclamation) which is true or false, but not both. 2.1.1. Examples: “Obama is president.” is a proposition. “Obama will be re-elected.” is not a proposition. 2.1.2. “This statement is false.” is a paradox that many would not consider a proposition. 2.1.3. For ECS 20, we will use p, q, and r to symbolize propositions, subpropositions, or logical variables which take true or false values. 2.2. Compound Proposition = a proposition that has its truth value completely determined by the truth values of two or more subpropositions and the operators (also called connectives) connecting them. 3. Basic Logical Operations 3.1. Conjunction = = “and.” If both p and q are true, then p q is true, otherwise p q is false.