Computer Cartograms
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Digital Mapping & Spatial Analysis
Digital Mapping & Spatial Analysis Zach Silvia Graduate Community of Learning Rachel Starry April 17, 2018 Andrew Tharler Workshop Agenda 1. Visualizing Spatial Data (Andrew) 2. Storytelling with Maps (Rachel) 3. Archaeological Application of GIS (Zach) CARTO ● Map, Interact, Analyze ● Example 1: Bryn Mawr dining options ● Example 2: Carpenter Carrel Project ● Example 3: Terracotta Altars from Morgantina Leaflet: A JavaScript Library http://leafletjs.com Storytelling with maps #1: OdysseyJS (CartoDB) Platform Germany’s way through the World Cup 2014 Tutorial Storytelling with maps #2: Story Maps (ArcGIS) Platform Indiana Limestone (example 1) Ancient Wonders (example 2) Mapping Spatial Data with ArcGIS - Mapping in GIS Basics - Archaeological Applications - Topographic Applications Mapping Spatial Data with ArcGIS What is GIS - Geographic Information System? A geographic information system (GIS) is a framework for gathering, managing, and analyzing data. Rooted in the science of geography, GIS integrates many types of data. It analyzes spatial location and organizes layers of information into visualizations using maps and 3D scenes. With this unique capability, GIS reveals deeper insights into spatial data, such as patterns, relationships, and situations - helping users make smarter decisions. - ESRI GIS dictionary. - ArcGIS by ESRI - industry standard, expensive, intuitive functionality, PC - Q-GIS - open source, industry standard, less than intuitive, Mac and PC - GRASS - developed by the US military, open source - AutoDESK - counterpart to AutoCAD for topography Types of Spatial Data in ArcGIS: Basics Every feature on the planet has its own unique latitude and longitude coordinates: Houses, trees, streets, archaeological finds, you! How do we collect this information? - Remote Sensing: Aerial photography, satellite imaging, LIDAR - On-site Observation: total station data, ground penetrating radar, GPS Types of Spatial Data in ArcGIS: Basics Raster vs. -

Chapter 13.2: Topographic Maps 1
Chapter 13.2: Topographic Maps 1 A map is a model or representation of objects and terrain in the actual environment. There are numerous types of maps. Some of the types of maps include mental, planimetric, topographic, and even treasure maps. The concept of mapping was introduced in the section using natural features. Maps are created for numerous purposes. A treasure map is used to find the buried treasure. Topographic maps were originally used for military purposes. Today, they have been used for planning and recreational purposes. Although other types of maps are mentioned, the primary focus of this section is on topographic maps. Types of Maps Mental Maps – The mind makes mental maps all the time. You drive to the grocery store. You turn right onto the boulevard. You identify a street sign, building or other landmark and know where this is where you turn. You have made a mental map. This was discussed under using natural features. Planimetric Maps – A planimetric map is a two dimensional representation of objects in the environment. Generally, planimetric maps do not include topographic representation. Road maps, Rand McNally ® and GoogleMaps ® (not GoogleEarth) are examples of planimetric maps. Topographic Maps – Topographic maps show elevation or three-dimensional topography two dimensionally. Topographic maps use contour lines to show elevation. A chart refers to a nautical chart. Nautical charts are topographic maps in reverse. Rather than giving elevation, they provide equal levels of water depth. Topographic Maps Topographic maps show elevation or three-dimensional topography two dimensionally. Topographic maps use contour lines to show elevation. -
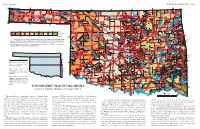
TOPOGRAPHIC MAP of OKLAHOMA Kenneth S
Page 2, Topographic EDUCATIONAL PUBLICATION 9: 2008 Contour lines (in feet) are generalized from U.S. Geological Survey topographic maps (scale, 1:250,000). Principal meridians and base lines (dotted black lines) are references for subdividing land into sections, townships, and ranges. Spot elevations ( feet) are given for select geographic features from detailed topographic maps (scale, 1:24,000). The geographic center of Oklahoma is just north of Oklahoma City. Dimensions of Oklahoma Distances: shown in miles (and kilometers), calculated by Myers and Vosburg (1964). Area: 69,919 square miles (181,090 square kilometers), or 44,748,000 acres (18,109,000 hectares). Geographic Center of Okla- homa: the point, just north of Oklahoma City, where you could “balance” the State, if it were completely flat (see topographic map). TOPOGRAPHIC MAP OF OKLAHOMA Kenneth S. Johnson, Oklahoma Geological Survey This map shows the topographic features of Oklahoma using tain ranges (Wichita, Arbuckle, and Ouachita) occur in southern contour lines, or lines of equal elevation above sea level. The high- Oklahoma, although mountainous and hilly areas exist in other parts est elevation (4,973 ft) in Oklahoma is on Black Mesa, in the north- of the State. The map on page 8 shows the geomorphic provinces The Ouachita (pronounced “Wa-she-tah”) Mountains in south- 2,568 ft, rising about 2,000 ft above the surrounding plains. The west corner of the Panhandle; the lowest elevation (287 ft) is where of Oklahoma and describes many of the geographic features men- eastern Oklahoma and western Arkansas is a curved belt of forested largest mountainous area in the region is the Sans Bois Mountains, Little River flows into Arkansas, near the southeast corner of the tioned below. -

What Is Geovisualization? to the Growing Field of Geovisualization
This issue of GeoMatters is devoted What is Geovisualization? to the growing field of geovisualization. Brian McGregor uses geovisualiztion to by Joni Storie produce animated maps showing settle- ment patterns of Hutterite colonies. Dr. Marc Vachon’s students use it to produce From a cartography perspective, dynamic presentation options to com- videos about urban visualization (City geovisualization represents a change in municate knowledge. For example, at- Hall and Assiniboine Park), while Dr. how knowledge is formed and repre- lases require extra planning compared Chris Storie shows geovisualiztion for sented. Traditional cartography is usu- to individual maps, structurally they retail mapping in Winnipeg. Also in this issue Honours students describe their ally seen a visualization (a.k.a. map) could include hundreds of maps, and thesis projects for the upcoming collo- that is presented after the conclusion all the maps relate to each other. Dr. quium next March, Adrienne Ducharme is reached to emphasize or compliment Danny Blair and Dr. Ian Mauro, in the tells us about her graduate research at the research conclusions. Geovisual- Department of Geography, provide an ELA, we have a report about Cultivate ization changes this format by incor- excellent example of this integration UWinnipeg and our alumni profile fea- porating spatial data into the analysis with the Prairie Climate Atlas (http:// tures Michelle Méthot (Smith). (O’Sullivan and Unwin, 2010). Spatial www.climateatlas.ca/). The combina- Please feel free to pass this newsletter data, statistics and analysis are used to tion of maps with multimedia provides to anyone with an interest in geography. answer questions which contribute to for better understanding as well as en- Individuals can also see GeoMatters at the Geography website, or keep up with the conclusion that is reached within riched and informative experiences of us on Facebook (Department of Geog- the research. -

Loading and Managing OS Mastermap Topography Layer
Loading and Managing OS MasterMap® Topography Layer An ESRI (UK) White Paper Confidentiality Statement This document contains information which is confidential to ESRI (UK) Limited. No part of this document should be reproduced or revealed to third parties without the express permission of ESRI (UK) Limited. © 2008 ESRI (UK) Ltd and its third party licensors. All rights reserved. ESRI (UK) Ltd Millennium House 65 Walton Street Aylesbury Buckinghamshire HP21 7QG Tel: +44 (0) 1296 745500 Fax: +44 (0) 1296 745544 Website: www.esriuk.com Released: 10/11/2008 Version: 5.3 Document History: Version Date Changes 1.0 31/08/2003 Document initial release. 2.0 16/12/2003 Document Updated/ Name Change. 3.0 23/11/2004 Document Reviewed/ Name Change. 4.0 05/06/05 OS MasterMap v6 4.1 11/08/05 Edits after Ordnance Survey review 5.0 19/05/2006 Technology updates 5.1 19/05/2006 Len Laver and Wai-Ming Lee review and edit of sections relevant to OS MasterMap-to-Go service 5.2 01/04/2008 Updated to new ESRI (UK) branding and style. 5.3 10/11/2008 Updates for new ‘minimise load on database’ option. © ESRI (UK) 2008 2 Contents Page 1. Introduction ........................................................................... 5 2. OS MasterMap® ...................................................................... 6 2.1. What is OS MasterMap? ............................................................... 6 2.2. Benefits of OS MasterMap ............................................................ 7 2.3. TOIDs and TOID-Associations ....................................................... 8 2.4. How OS MasterMap Topography Layer is Structured ........................ 9 2.5. OS MasterMap Topography Layer Data Schema ............................. 10 3. OS MasterMap Topography Layer Data Supply ................... 16 3.1. Initial OS MasterMap Topography Layer Data Supply ..................... -

The Topography of the Earth's Surface
CHAPTER 3 THE LAY OF THE LAND: THE TOPOGRAPHY OF THE EARTH’S SURFACE 1. LATITUDE AND LONGITUDE 1.1 You probably know already that the basic coordinate system that’s used to describe the position of a point on the Earth's surface is latitude and longitude. In this system (Figure 3-1), the Earth is imagined to be cut by a series of planes that pass through the north–south axis of rotation. The intersection of such a plane with the Earth’s surface is called a line (really a curve) of longitude, or a meridian. Longitude is measured in degrees, from zero to 360. One meridian (the one that passes through Greenwich, England) is called the prime meridian, and longitude is measured 180 degrees to the west of that and 180 degrees to the east of that. The opposite meridian, 180 degrees around the world from the prime meridian (and the intersection of the longitude plane with the other side of the world) lies about in the middle of the Pacific Ocean. 1.2 One consequence of this definition of longitude is that the spacing between two meridians gets smaller as you go north or south from the equator. Think about this the next time you fly west in a jetliner: You would have to move awfully fast to keep up with the sun, and land at the same time of day you took off, if you're flying along the equator, but if you're flying east to west in the far north or far south on the earth, you could easily arrive at your destination a lot earlier in the day than you took off! 1.3 The other element of the coordinate system is a series of latitude circles (Figure 3-1). -

Bibliographical Index
Bibliographical Index BIBLIOGRAPHICAL ACCESS TO THIS VOLUME Bacon, Roger. Opus Majus. 305, 322, 345 Basil, Saint. Homilies. 328 Three modes of access to bibliographical information are used Bede, the Venerable. De natura rerum. 137 in this volume: the footnotes; the bibliographies; and the Bib ---. De temporum ratione. 321 liographical Index. The footnotes provide the full form of a reference the first Cassiodorus. Institutiones divinarum et saecularium time it is cited in each chapter with short-title versions in litterarum. 172, 255, 259, 261 subsequent citations. In each of the short-title references, the Cato the Elder. Origines. 205 note number of the fully cited work is given in parentheses. Censorinus. De die natalie 255 The bibliographies following each chapter provide a selec Chaucer, Geoffrey. Prologue to the Canterbury Tales. 387 tive list of major books and articles relevant to its subject Cicero. Arataea (translation of Aratus's versification of matter. Eudoxus's Phaenomena). 143 The Bibliographical Index comprises a complete list, ar ---. Letters to Atticus. 255 ranged alphabetically by author's name, of all works cited in ---. De natura deorum. 160,168 the footnotes. Numbers in bold type indicate the pages on --. The Republic. 159, 160, 255 which references to these works can be found. This index is ---. Tusculan Disputations. 160 divided into two parts. The first part identifies the texts of Cleomedes. De motu circulari. 152, 154, 169 classical and medieval authors. The second part lists the mod Cosmas Indicopleustes. Christian Topography. 143, 144, ern literature. 261 Ctesias of Cnidus. Indica. 149 TEXTS OF CLASSICAL AND MEDIEVAL ---. Persica. 149 AUTHORS Dicuil. -

Application of GIS in Determination and Mapping of Topographic
International Journal of Chemical Studies 2019; 7(2): 1092-1097 P-ISSN: 2349–8528 E-ISSN: 2321–4902 IJCS 2019; 7(2): 1092-1097 Application of GIS in determination and © 2019 IJCS Received: 11-01-2019 mapping of topographic characteristics of Accepted: 15-02-2019 temperate Himalaya Owais Bashir Division of Soil Science and Agricultural Chemistry, Sher-E- Owais Bashir, Tahir Ali, D Ram, GH Rather, Nageena Nazir, QAH Dar Kashmir University of Agricultural Sciences And Technology of and Perminder singh Kashmir, Jammu and Kashmir India Abstract For the understanding and management of physical environment the mapping and visualization of Tahir Ali topographic information is of great importance. Researchers all over the world are using GIS software in Division of Soil Science and Agricultural Chemistry, Sher-E- their investigation because it has proved to be a successful tool for sustainable development. In view to Kashmir University of Agricultural contemporary cartographic output the application of GIS in landscape mapping and visualization has Sciences And Technology of increased many folds. The main objective of this paper is to determine the application of GIS software to Kashmir, Jammu and Kashmir analyze the topographical data. The application of GIS in mapping and visualization has occurred due to India advances in computer technology. For the perceived user needs and the technology that allows faster visual display, GIS uses the idea of visualization through maps. For manipulation and extraction of D Ram terrain features DEM based topographic data of the study region was entered in the GIS softwares. Some Division of Soil Science and Agricultural Chemistry, Sher-E- important topographic features were generated and extracted that built GIS assisted topographical data Kashmir University of Agricultural such as contour and spot height, slope and relief direction, drainage and hill shade. -

Ordnance Survey® Mastermap® Topographic Layer
Product Brochure Vector Mapping Data Ordnance Survey® MasterMap® Topographic Layer Product Overview Value Added Supply OS MasterMap® Topographic Layer provides vector mapping At no additional cost: which can be overlaid with your data, to provide contextual Optimised value added, work-ready format mapping. This allows for intuitive and informative outputs, Established quality assured processes enabling faster decision-making. Vector mapping allows the Standard format symbology of the base maps to be customised, and queried Reduces setup overheads and administrative costs through the attribute table. OS MasterMap® Topographic Layer Value Added Supply Large Scale background map data includes: Individual buildings, roads and areas of land Generation of a non-tiled national vector dataset with feature In excess of 400 million individual features, each attributed to continuity one of 9 themes Re-structured data feature layers Rich topographic data content Optimised formats for Esri users Uncluttered and clean mapping OS Open Data™ (Strategi®, VectorMap® Most detailed background map District and OpenMap Local) supplied free of charge for Great Britain coverage Area of Interest bought, providing background mapping which Scale range: 1:1,250 to 1:10,000 can be viewed at smaller scales British National Grid Projection (OSGB36) Layer files and map documents (mxd’s) ensuring quick and Full supply file-geodatabase delivery size: approximately easy access to the data, with consistent symbolisation across 120GB Open data and MasterMap® Topographic Layer Full feature level metadata Bulk load service Product Brochure Contents Data layers re-structured from original supply into feature groups or individual layers to ensure the data can be used effectively and as flexibly as possible. -

Topographic Analysis and Predictive Modeling Using Geographic Information Systems Steven Hall Clemson University, [email protected]
Clemson University TigerPrints All Dissertations Dissertations 12-2008 Topographic Analysis and Predictive Modeling using Geographic Information Systems Steven Hall Clemson University, [email protected] Follow this and additional works at: https://tigerprints.clemson.edu/all_dissertations Part of the Agriculture Commons Recommended Citation Hall, Steven, "Topographic Analysis and Predictive Modeling using Geographic Information Systems" (2008). All Dissertations. 322. https://tigerprints.clemson.edu/all_dissertations/322 This Dissertation is brought to you for free and open access by the Dissertations at TigerPrints. It has been accepted for inclusion in All Dissertations by an authorized administrator of TigerPrints. For more information, please contact [email protected]. TOPOGRAPHIC ANALYSIS AND PREDICTIVE MODELING USING GEOGRAPHIC INFORMATION SYSTEMS A Dissertation Presented to the Graduate School of Clemson University In Partial Fulfillment of the Requirements for the Degree Doctor of Philosophy Forest Resources by Steven Thomas Hall December 2008 Accepted by: Dr. Chris J. Post, Committee Chair Dr. Elena A. Mikhailova Dr. Thomas A. Waldrop Dr. Patrick D. Gerard i ABSTRACT This dissertation describes three GIS models developed to better model topographic features and the occurrence of mountain laurel (Kalmia latifolia) in the southern Appalachian Mountains. The first study presented “A LiDAR based GIS model to calculate Terrain Shape Index on a landscape scale”, attempts to develop a GIS based model to calculate the Terrain Shape Index (TSI). TSI is typically collected in the field using a series of elevation measurements to determine the average elevation change within the study plot. In this study, a GIS model is developed and TSI values compared to those collected using conventional methods. -

Digital Outlines and Topography of the Glaciers of the American West
Prepared in cooperation with the Departments of Geology and Geography, Portland State University, Portland, Oregon Digital Outlines and Topography of the Glaciers of the American West Open-File Report 2006–1340 U.S. Department of the Interior U.S. Geological Survey Cover. Map showing distribution of glaciers in the American West. Prepared in cooperation with the Departments of Geology and Geography, Portland State University, Portland, Oregon Digital Outlines and Topography of the Glaciers of the American West By Andrew G. Fountain, Matthew Hoffman, Keith Jackson, Hassan Basagic, Thomas Nylen, and David Percy Open-File Report 2006–1340 U.S. Department of the Interior U.S. Geological Survey iii U.S. Department of the Interior DIRK KEMPTHORNE, Secretary U.S. Geological Survey Mark D. Myers, Director U.S. Geological Survey, Reston, Virginia: 2007 For product and ordering information: World Wide Web: http://www.usgs.gov/pubprod Telephone: 1-888-ASK-USGS For more information on the USGS—the Federal source for science about the Earth, its natural and living resources, natural hazards, and the environment: World Wide Web: http://www.usgs.gov Telephone: 1-888-ASK-USGS Suggested citation: Fountain, A.G., Hoffman, Matthew, Jackson, Keith, Basagic, Hassan, Nylen, Thomas, and Percy, David, 2007, Digital outlines and topography of the glaciers of the American West: U.S. Geological Survey Open-File Report 2006–1340, 23 p. Any use of trade, product, or firm names is for descriptive purposes only and does not imply endorsement by the U.S. Government. Although this report is in the public domain, permission must be secured from the individual copyright owners to reproduce any copyrighted material contained within this report. -

Geographic Information System Software Selection Guide July 2013
System Assessment and Validation for Emergency Responders (SAVER) Geographic Information System Software Selection Guide July 2013 Prepared by Space and Naval Warfare Systems Center Atlantic Approved for public release; distribution is unlimited. The Geographic Information System Software Selection Guide was funded under Interagency Agreement No. HSHQPM-12-X-00031 from the U.S. Department of Homeland Security, Science and Technology Directorate. The views and opinions of authors expressed herein do not necessarily reflect those of the U.S. Government. Reference herein to any specific commercial products, processes, or services by trade name, trademark, manufacturer, or otherwise does not necessarily constitute or imply its endorsement, recommendation, or favoring by the U.S. Government. The information and statements contained herein shall not be used for the purposes of advertising, nor to imply the endorsement or recommendation of the U.S. Government. With respect to documentation contained herein, neither the U.S. Government nor any of its employees make any warranty, express or implied, including but not limited to the warranties of merchantability and fitness for a particular purpose. Further, neither the U.S. Government nor any of its employees assume any legal liability or responsibility for the accuracy, completeness, or usefulness of any information, apparatus, product, or process disclosed; nor do they represent that its use would not infringe privately owned rights. Distribution authorized to Federal, state, local, and tribal government agencies for administrative or operational use, July 2013. Other requests for this document shall be referred to the SAVER Program, U.S. Department of Homeland Security, Science and Technology Directorate, OTE Stop 0215, 245 Murray Lane, Washington, DC 20528-0215.