DOCSLIB.ORG

Review to the Duckworth-Lewis Method Using Data Mining Techniques

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Review to the Duckworth-Lewis Method Using Data Mining Techniques Imperial Journal of Interdisciplinary Research (IJIR) Vol-2, Issue-5, 2016 ISSN: 2454-1362, http://www.onlinejournal.in Review to the Duckworth-Lewis Method Using Data Mining Techniques Rohan Brahme1*, Roshan Birar2, Poonam Kadnar3 & Prof. Suruchi Malao4 1,2,3,4Department of Computer Engineering, K. K. Wagh Institute of Engg. Education & Research, Savitribai Phule Pune University, India Abstract- The Duckworth - Lewis system represents mathematical formulation used to get a target score B. Duckworth-Lewis Method for cricket matches interrupted by bad weather Two British statisticians Frank Duckworth and conditions. The Duckworth-Lewis (D/L) method Tony Lewis developed their Method called considers only two factors to provide updated target Duckworth-Lewis (D/L) method which is nothing but i.e. number of runs which can be scored in the a statistical method used to predict the target score of remaining innings as a function of the number of the team batting second in a limited overs game which overs remaining and the number of wickets in hand. is interrupted by unavoidable circumstances. The D/L We will be using WEKA tool to find bias in current method, a system based on mathematical model D/L system and capably illustrate those. considers only two resources – wickets left and overs Duckworth Lewis system has observed to be remaining. When overs are lost, setting an adjusted biased towards the team batting first and the team target is not as simple as to reduce the batting team’s winning the toss from the scenarios like interruption target proportionally, because a team batting second of the game for multiple times in same match and fall with wickets in hand can be expected to play more wickets in death overs while batting second. Bias in aggressively than one with full 50 over’s and hence the context of the outline is defined as taking can achieve a higher run rate. So then Duckworth & advantage of the assets of systems such as the Lewis (1998) considered the most common situation D/Lewis method. We also explore to show that such where two terms play a full length game. taking advantage of the system permits prediction of the result of the match winner which is better than just chance. Using the above analysis, we propose a modification to the existing Duckworth Lewis system by considering the observed patterns from the dataset as an additional resource to reduce the bias along with the existing resources to predict the target score. Keywords- Cricket, Duckworth - Lewis, WEKA, C4.5, Decision Trees. I. INTRODUCTION A. The game of Cricket The above graph [1] shows the percentage of As mentioned in [1]. Cricket is a bat-and-ball team resources remaining for a team to the number of overs sport that is originated in England and is one of the bowled. As we see it in an exponential graph reducing most popular games in the world. Moving on from the as more number of wickets keep falling and comes conventional Test cricket, it has slowly ventured into down to zero when the 9th wicket falls. Duckworth- limited over formats like ODI and T20 so that a Lewis observed a close connection between the definite result is obtained, making it more entertaining availability of these resources and team’s final score, as a spectator sport. Sometimes due constraints like which this algorithm tries to exploit. bad weather (rain, sandstorms and bad lights), In above table the remaining overs are plotted floodlight failure and crowd issue certain amount of against wickets lost. overs are lost and hence a definite result isn’t obtained. To overcome these obstacles methods have been devised to revise target scores and/or declare a winner. Imperial Journal of Interdisciplinary Research (IJIR) Page 547 Imperial Journal of Interdisciplinary Research (IJIR) Vol-2, Issue-5, 2016 ISSN: 2454-1362, http://www.onlinejournal.in 1. South Africa vs. New Zealand, Durban, November 2000 Batting first for New Zealand and score was 81 for 5 after 27.2 overs when rain reduced the game to 49 overs per side. Then, with New Zealand on 114 for 5 in 32.4, their innings was stopped due to rain, and the second innings was shortened to 32 overs. South Africa's got new target according to the D/L charts was 153, but modified version suggests that the target would have been 156. At the time when game was interrupted, New Zealand's run rate was 3.48 for five wickets down and 17.2 overs to spare. Resource Percentage Table According to D/L's modified calculations, South Africa's required run rate would be The above table [3] is the calculation of percentage 4.87. of resources left. Here the percentage of resources are calculated beforehand by taking into consideration of 2. West Indies vs. New Zealand, Port-of- the overs left and the wickets lost and is stored in the Spain, 2002 table so that it comes in handy while calculating the New Zealand made 212 for 5 in 44.2 revised target. This table is actually referred to while overs while batting first, when their Duckworth Lewis comes into picture. innings was called off and West Indies' However, some of the factors like the toss may chase was truncated to 33 overs. D/L play a crucial role while deciding the winner since it calculated their revised target at the time involves a lot of speculation and research while as 212. Again, a comparison of run rates deciding bat or field first after winning the toss. For raises a few questions. New Zealand's run example, the analysis of pitch report, previous history rate at the end of their innings was 4.78; of the ground, and expected weather conditions and West Indies' required rate in 33 overs these factors that suggests the decision. In rain according to D/L is 6.36, an increase of affected matches the batting first is the advantageous 33%. decision. After rain, the pitch becomes soft and outfield becomes slow and the ball bounces unevenly, 3. South Africa vs. New Zealand, making it difficult to bat as mentioned in [2]. Johannesburg, WC2003 Replying to South Africa's imposing 306 C. Duckworth-Lewis Model for 6 in 50 overs, New Zealand, riding on Objective of D/L system was to find method that Stephen Fleming's outstanding century, must follow the criteria given below. were 182 for 1 in 30.2 when rain reduced 1. It must maintain exact fairness to both the chase to 39 overs. According to the sides. new D/L calculations, the revised target 2. It must give appropriate result in all would have been 229 (it was 226 at the possible situations. time). The point of contention is this: at 3. Team 1’s scoring pattern should not affect the time of the interruption, New the revised target for team 2 in an Zealand's required rate was 6.35 runs per interrupted game. over, stretching over a period of almost 20 The interruption of game for multiple times during overs. Going by the current D/L same match and the fall of wickets in death overs calculations, the required run rate on cause the unfair dealing with target prediction. So the resumption is 5.42, over a period of just data mining to reduce such bias in specific conditions 8.4 overs - obviously, the rain has should be done. simplified New Zealand's task enormously (though the D/L contention is that New Zealand are reaping the rewards of being D. Controversial D/L method decided well ahead of the par score at the point of matches [2] interruption). Some actual scenarios from ODIs that highlight the shortcomings in D/L method: Imperial Journal of Interdisciplinary Research (IJIR) Page 548 Imperial Journal of Interdisciplinary Research (IJIR) Vol-2, Issue-5, 2016 ISSN: 2454-1362, http://www.onlinejournal.in E. Formula for D/L score calculation[6] in death over cause unfair result if inning gets Let, truncated. S: Team 1’s score [4] We are going to these tools to extract such R1: Resources % available to team 1 (from R. P. patterns and will try to minimise bias. This is the table) foundation for evaluation part of the project and base R2: Resources % available to team 2 (from R. P. input for extension part. table) Following are some observed patterns [2]: T: Target score for team 2 1. Pattern 1: Team winning the toss wins the matches in 66% cases. Case 1: 2. Pattern 2: Team batting first wins the If R1>R2, match in 64% cases. T=S(R1/R2)+1; 3. Pattern 3: 54% of teams winning toss Reduces team’s score in proportion to reduction in elects to field first in the rain affected resources matches. 4. Pattern 4: Average of difference in run Case 2: rate between winning and losing team If R1=R2, scores is not significant T=S+1; No adjustment required A. Inferences from the above patterns[2] 1. D/L method has been biased towards the Case 3: team batting 1st. If R1<R2; 2. D/L method has been biased towards the T=S+[G50*(R2-R1)/100]+1; team winning the toss. Where G50 for matches involving ICC full 3. D/L method stresses more on wickets member nations, at present is 235 rather than run rate and the runs scored. Increase team 2 target score by the extra runs that are predicted in accordance with the extra resources Based on the above observations, we have a heuristic model to predict the winner in a match F.
Load more

Recommended publications
  • Arxiv:1908.07372V1 [Physics.Soc-Ph] 12 Aug 2019 We Introduce the Concept of Using SDE for the Game of Cricket Using a Very Rudimentary Model in Subsection 2.1
    Stochastic differential theory of cricket Santosh Kumar Radha Department of physics *Case Western Reserve University Abstract A new formalism for analyzing the progression of cricket game using Stochastic differential equa- tion (SDE) is introduced. This theory enables a quantitative way of representing every team using three key variables which have physical meaning associated with them. This is in contrast with the traditional system of rating/ranking teams based on combination of different statical cumulants. Fur- ther more, using this formalism, a new method to calculate the winning probability as a progression of number of balls is given. Keywords: Stochastic Differential Equation, Cricket, Sports, Math, Physics 1. Introduction Sports, as a social entertainer exists because of the unpredictable nature of its outcome. More recently, the world cup final cricket match between England and New Zealand serves as a prime example of this unpredictability. Even when one team is heavily advantageous, there is a chance that the other team will win and that likelihood varies by the particular sport as well as the teams involved. There have been many studies showing that unpredictability is an unavoidable fact of sports [1], despite which there has been numerous attempts at predicting the outcome of sports [5]. Though different, there has been considerable efforts directed towards predicting the future of other fields including financial markets [4], arts and entertainment award events [6], and politics [7]. There has been a wide range of statistical analysis performed on sports, primarily baseball and football[8,2,3] but very few have been applied to understand cricket. Complex system analysis[9], machine learning models[10, 12] and various statical data analysis[13, 14, 15, 16, 17] have been used in previous studies to describe and analyze cricket.
    [Show full text]
  • Winning and Score Predictor (Wasp) Tool
    WINNING AND SCORE PREDICTOR (WASP) TOOL 1 2 3 Anik Shah , Dhaval Jha , Jaladhi Vyas 1,2Department of Computer Science & Engineering, Nirma University, Ahmadabad, Gujarat, (India) ABSTRACT Winning and Score Predictor (WASP) is a calculation tool used in cricket to predict the scores and possible results of a limited over match format, e.g. One Day and Twenty-20 (T-20) matches. The prediction is based on the factors such as the ease of scoring on the day, according to the pitch, weather and boundary size. For the team batting first, it gives the prediction of the final total. For the team batting second, it gives the probability of the chasing team winning, although it does not take the match situation into the equation. Predictions are based on the average team playing against the average team in those conditions. Here we have proposed an advanced and modified method for calculating the score. Keywords: Dynamic Programming, Predictor tool, ODIs, T-20, WASP. I. INTRODUCTION For years while watching limited overs cricket, we have seen projected scores at different intervals being displayed on our television screens. But in one of the match played between New Zeland and India, something different in the form of WASP (Winning and Score Prediction) was shown. In this paper, we have a look to differentiate between the two and explain what WASP brings to the table. WASP was first introduced by Sky Sport New Zealand on November 2012 during Auckland's HRV Cup Twenty20 game against Wellington. The WASP technique is a product of some extensive research from PhD graduate Dr.
    [Show full text]
  • Race and Cricket: the West Indies and England At
    RACE AND CRICKET: THE WEST INDIES AND ENGLAND AT LORD’S, 1963 by HAROLD RICHARD HERBERT HARRIS Presented to the Faculty of the Graduate School of The University of Texas at Arlington in Partial Fulfillment of the Requirements for the Degree of DOCTOR OF PHILOSOPHY THE UNIVERSITY OF TEXAS AT ARLINGTON August 2011 Copyright © by Harold Harris 2011 All Rights Reserved To Romelee, Chamie and Audie ACKNOWLEDGEMENTS My journey began in Antigua, West Indies where I played cricket as a boy on the small acreage owned by my family. I played the game in Elementary and Secondary School, and represented The Leeward Islands’ Teachers’ Training College on its cricket team in contests against various clubs from 1964 to 1966. My playing days ended after I moved away from St Catharines, Ontario, Canada, where I represented Ridley Cricket Club against teams as distant as 100 miles away. The faculty at the University of Texas at Arlington has been a source of inspiration to me during my tenure there. Alusine Jalloh, my Dissertation Committee Chairman, challenged me to look beyond my pre-set Master’s Degree horizon during our initial conversation in 2000. He has been inspirational, conscientious and instructive; qualities that helped set a pattern for my own discipline. I am particularly indebted to him for his unwavering support which was indispensable to the inclusion of a chapter, which I authored, in The United States and West Africa: Interactions and Relations , which was published in 2008; and I am very grateful to Stephen Reinhardt for suggesting the sport of cricket as an area of study for my dissertation.
    [Show full text]
  • Rules Will Be in Effect (Except Free Hit)
    TENNISBALL CRICKET ASSOCIATION P a g e | 1 2016 TCA Confidential| BAY AREA CHAPTER 2016 FLT+ Copyright © 2003-2016 by Tennisball Cricket Association. All rights reserved. 870 Corriente Point Dr, Redwood City, CA 94065 ICC 2000 Code 2nd Edition – 2003 are Copyright of Marylebone Cricket Club (MCC). No part of this document may be reproduced in any form without prior written permission of the copyright holder. The information contained herein and on the website and on other communique of TCA, including but not limited to member e-mails, e-mail aliases mentioned in this document are properties of TCA. Unauthorized use of this property or disclosure of any information without prior written approval of the TCA constitutes a criminal offense. TCA reserve the right to make changes to this document without notice and without incurring any liability. The information is provided in this document “as is” and is subject to change without notice. P a g e | 2 2016 TCA Confidential| REGISTRATION AND MEMBERSHIP Registration Deadline: Sep 4, 2016 (via web document) . Registration documents can be found here: http://tennisballcricket.com/2016-registration . Regular Mail: TCA, 870 Corriente Point Dr, Redwood City, CA 94065 . Email: [email protected] . FEE: $350/team (FLT+ tournament only) TOURNAMENT SUMMARY Format Max # of Teams: 48 Round Robin Grouping: 12 groups (A to L) of 4 teams each. Team will play across groups. Groups: A vs L B vs K C vs J D vs I E vs H F vs G After Round if the points are the same, the tie breaker will be Number of wins than Ties than Losses than DRR than Rank at start of round.
    [Show full text]
  • MONITORING a CRICKET MATCH IIT Madras April 3, 2016
    MONITORING A CRICKET MATCH IIT Madras April 3, 2016 1. Introduction Various sensors at Accenture used for monitoring Project Development Cycle will record and report the occurrences of various events like over budget, deadline missed, resources overused etc. These recordings can be both numeric and textual with which we try to monitor the project development and performance by a team at Accenture. We believe this is similar to monitoring the performance of the team on strike in the second innings of a cricket match. The team has a target to chase, and at any given point, its resources, used and remaining, are wickets and number of overs. The simplest thing to do is to keep track of the required run rate, and perhaps make a recommendation - which could, for example, be about which batsman should come in next, or whether a player is doing well by “rotating strike”. Such observations and recommendations will also draw upon other information, for example historical strike rate of a player, current form of a player, the state of the pitch and whether the first team is above or below par (as decided by some commentator), the number of overs remaining for key bowlers etc. Such a system could be built given the numerical data associated with each ball as well as the historical data. A more sophisticated system, on the other hand, could extract more information from the text of the commentary, for example when catches are dropped, a ball is mis-fielded, an overthrow, or a change in field placement. Such a system needs data not only in the numeric form, but also in the form of spoken / written text about the match, as well as from the contextual information.
    [Show full text]
  • Effectiveness of Top 3 Batsmen Helping Team in Winning ODI Matches
    Yadav et al (2020): Effectiveness of batsmen towards wining Nov 2020 Vol. 23 Issue 17 Effectiveness of Top 3 Batsmen helping team in Winning ODI Matches Cintukumar Yadav1, Amritashish Bagchi2*, Antriksh Jaiswal3 and Jayvrat Kapoor4 1,3,4Student, MBA, 2Assistant Professor,Symbiosis School of Sports Sciences, Symbiosis International (Deemed University), Pune, Maharashtra, India *Corresponding author: [email protected] (Bagchi) Abstract Background:This Research paper tells us about how effective a role Top 3 batsman plays in competitive cricket. Cricket has become one of the majorly-watched sport across the globe in recent years. Over the years the game of cricket has evolved drastically with changes in formats and also playing style and strategy. Winning a game of cricket depends on many factors like winning the toss, home advantage, player combination, team composition and, individuals’ performance, this research paper takes into consideration the impact of the top 3 batsmen helping a team to score a big total (runs) in ODIs.Methods: The teams that have been selected for the study are the current top 5 ranked teams in ICC’s latest ODI Rankings - England, India, New Zealand, South Africa and Australia ranked 1,2,3,4 and 5 respectively, the number of times they have scored more than 300 runs and the contribution of Top 3 Batsman’s.Conclusion. The study will act as valuable aid and help the team management to select the right combination of players at Top 3 in the playing XI to win the match. The contribution of Top 3 Batsman’s had an impact on the match result, researchers have found that when team scoring more than 300, their team has won the match 80.7% of times.
    [Show full text]
  • Assessing Decision Rules for Stopped Cricket Games Assessing Decision Rules for Stopped Cricket Games
    Assessing Decision Rules For Stopped Cricket Games Assessing decision rules for stopped cricket games Ahsan Bhatti, B. Sc., A. Stat A project Submitted to the School of Graduate Studies in Partial Fulfilment of the Requirements for the Degree of Master of Science McMaster University c 2015 Ahsan Bhatti i Master of Science (2015) McMaster University Statistics Hamilton, Ontario TITLE: Assessing Decision Rules For Stopped Cricket Games AUTHOR: Ahsan Bhatti SUPERVISOR: Professor Ben Bolker NUMBER OF PAGES: ix, 75 ii Abstract In interrupted limited overs cricket games, teams do not always get a chance to finish the full game. In such cases, different methods can be used to establish which team wins. The method currently in use is called the Duckworth-Lewis method; it was introduced at the international level in 1998. The purpose of this project is to investigate and check the accuracy of Duckworth-Lewis method and make statistical comparisons with other proposed methods. The accuracy is checked via bias estimation, Cohen's Kappa and root mean square error methods; cross-validation is used to assess out-of-sample accuracy. The resource table, a summary of the expected fraction of total runs scored by a given point in the game, has missing values and monotonicity flaws. To improve the resource table, different statistical methods such as isotonic regression and Gibbs sampling, are used to construct different resource surfaces. The accuracy results show that the Duckworth- Lewis displays the lowest accuracy out of all the methods; whereas, the improved Duckworth-Lewis is more accurate at predicting the new target or results of stopped games.
    [Show full text]
  • Fairness and Incentive in Interrupted Cricket Matches∗
    Cricket interruptus: fairness and incentive in interrupted cricket matches∗ Michael Carter and Graeme Guthrie† October 26, 2002 Abstract We present a new adjustment rule for interrupted cricket matches that equalizes the probability of winning before and after the interruption. Our proposal differs from existing rules in the quantity preserved (the probability of winning), and also in the point at which it is measured (the time of interruption). We claim this is both fair and free of incentive effects. We give several examples of how our rule could have been applied in past matches, including some in which the ultimate result might have been different. The game of cricket is an immensely popular participatory and spectator sport in Britain and its former colonies in Africa (South Africa and Zimbabwe), Australasia (Australia and New Zealand), the Indian subcontinent (Bangladesh, India, Pakistan, Sri Lanka), and the West Indies. Traditionally, an international cricket match (“test match”)is played over five days and, more often than not, it ends in a draw. It is a game for afficionados. Recognising the potential popular appeal of a shorter game that provided a decisive result, the Australian media magnate Kerry Packer pioneered the introduction of a one-day game in the 1970s. Since then, the game has flourished commercially as a television sport, becoming the second most popular (after football)spectator sport. International teams travel the world, playing a mixture of one-day games and the traditional test matches. Annual one-day tournaments are held in Australia and Sharjah. Every four years, all major cricketing nations compete in the World Cup to produce an international champion.
    [Show full text]
  • Tolchards Devon Cricket League Playing Rules –2020 45/45 Overs
    Tolchards Devon Cricket League Playing Rules –2020 45/45 Overs 1 General a. All teams will be scheduled to play each other on a home and away basis determined by the Fixtures Secretary. All matches shall be of one innings of limited overs, one innings duration per team. b. Independent Umpires will be appointed by DACO for all Tier 1 groups Independent Umpires will be appointed by DACO for all Tier 2 groups except group South 2 and two teams from group West 1 and East 2 (prior informed). c. Each team shall supply one non-playing Scorer. Failure by any side to provide a Scorer for both innings shall result in 2 points being deducted from that side for the match concerned. d. Each team shall score the match live, on-line using a suitable scoring program, for example ‘Total Cricket Scorer’ or ‘ECB Play Cricket Scorer Pro’, with DLS available on each Scorer’s laptop. e. The provision of Wi-Fi by the home club for each of the Scorers is required. Failure of either Scorer or Club to meet these conditions shall result in 2 points being deducted from that side for the match concerned. If there is an operational failure of the technology, then the sanction will not be enforced. The Umpires will be responsible for reporting this offence on the Facilities Report. 2 Conduct of Matches Matches shall be conducted in accordance with the MCC Laws of Cricket (amended as at 1st April 2019) except for matters specifically provided within the Playing Rules that follow: a.
    [Show full text]
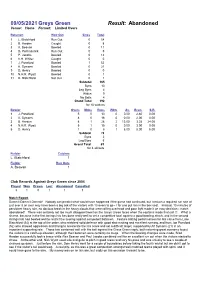
  • 09/05/2021Greys Green Result: Abandoned
    09/05/2021 Greys Green Result: Abandoned Venue: Home Format: Limited Overs Batsmen How Out Sixes Total 1 L. Blatchford Run Out 0 54 2 B. Harden Caught 0 8 3 A. Beavan Bowled 0 11 4 D. Penhallurick Run Out 0 5 5 P. Jacobs Bowled 0 12 6 K.H. Whiter Caught 0 0 7 J. Ponsford Bowled 1 52 8 A. Symons Bowled 0 21 9 D. Henry Bowled 0 0 10 N.H.R. Wyatt Bowled 0 1 11 R. Blatchford Not Out 0 1 Subtotal 165 Byes 10 Leg Byes 4 Wides 9 No Balls 4 Grand Total 192 for 10 wickets Bowler Overs Mdns Runs Wkts Av. Econ. S.R. 1 J. Ponsford 5 0 13 0 0.00 2.60 0.00 2 A. Symons 8 0 16 0 0.00 2.00 0.00 3 B. Harden 8 1 26 2 13.00 3.25 24.00 4 N.H.R. Wyatt 5 1 15 0 0.00 3.00 0.00 5 D. Henry 1 0 8 1 8.00 8.00 6.00 Subtotal 78 Byes 2 Leg Byes 5 Grand Total 85 for 4 wickets Fielder Catches L. Blatchford 1 Fielder Run Outs A. Beavan 1 Club Records Against Greys Green since 2004 Played Won Drawn Lost Abandoned Cancelled 3 1 0 1 1 1 Match Report Dammit Dammit Dammit! Nobody can predict what would have happened if the game had continued, but I reckon a required run rate of just over 8 an over may have been a big ask of the visitors with 13 overs to go - I for one put Isis in the box seat.
    [Show full text]
  • World Cup Cricket, England, 1983
    World Cup Cricket, England, 1983 With the elevation of Sri Lanka to Test status, only one place was available through qualification at the ICC Trophy, held in England in 1982. The newcomers, Zimbabwe, dominated the competition, defeating Bermuda in the final. There was a change of format, with again two groups of four, but this time they played each other twice each, thus doubling the number of matches played. The West Indies, still with Greenidge, Haynes, Richards and Lloyd at the top of the order, and Marshall, Roberts, Garner and Holding forming a strong pace attack, were hot favourites. Group A England, Pakistan, New Zealand, and Sri Lanka contested this group. England got off to a flying start, with a surprisingly easy win over New Zealand. Lamb made a fine century, and Snedden became the only bowler ever to concede over 100 runs in a World Cup match with figures of 12-1-105-2. England's 322/6 was too much for New Zealand despite 95 from Martin Crowe, with Willis taking 2/9 off 7 overs. Mohsin Khan, Zaheer Abbas, Javed Miandad and Imran Khan all had half centuries as Pakistan made hay against the Sri Lankan bowling in their first match. Despite 72 from Kuruppu and 59 from the number 9 bat, de Alwis, Sri Lanka were always behind the required run rate, and Pakistan won by 50 runs. When England took on Sri Lanka two days later the scoreline was almost identical. England made 333, with Gower contributing a superb 130, and Sri Lanka this time got to within 47 runs, Mendis with a 50 and de Alwis, promoted to 8, 58*.
    [Show full text]
  • How to Enter Scoresheet on Website
    How to Enter Scoresheet 1. Go to following website using your computer. Please note update scoresheet doesn’t work from CricClubs APP or from Mobile. You have to use the computer. http://phillymetrocricketleague.com/ OR https://cricclubs.com/PMCL 2. Use login button at top right corner to go to login screen. Login button is shown in below screen 3. At login screen enter your login details and hit SIGN IN button as shown below. If you don’t have it please send email to [email protected]. 4. On signing in you will be taken to default screen which shows your profile. Click Matches from top menu bar and click schedule as shown below 5. Next screen will take you to schedule and shows ADMIN ACTION drop down for games you are assigned umpiring. 6. Click Admin Action and Full card as shown below screen. 7. From the below screen please choose who won the toss, who is batting first and number of overs in the game 8. Select Batsman name, how out, bowler name from drop down and enter number of runs, number of balls, number of fours , sixers for each player. 9. Enter for each player as shown above. Enter Byes, Leg byes 10. Enter bowling figures. Once you enter wides and no balls in bowling figures it will automatically added to score above. 11. Enter details for both innings select man of the match, enter your name as an umpire and hit validate button at bottom of the screen 12. Once you hit validate button it will show you the scoresheet.
    [Show full text]