Polarization Due to Rotational Distortion in the Bright Star Regulus
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Thursday, December 22Nd Swap Meet & Potluck Get-Together Next First
Io – December 2011 p.1 IO - December 2011 Issue 2011-12 PO Box 7264 Eugene Astronomical Society Annual Club Dues $25 Springfield, OR 97475 President: Sam Pitts - 688-7330 www.eugeneastro.org Secretary: Jerry Oltion - 343-4758 Additional Board members: EAS is a proud member of: Jacob Strandlien, Tony Dandurand, John Loper. Next Meeting: Thursday, December 22nd Swap Meet & Potluck Get-Together Our December meeting will be a chance to visit and share a potluck dinner with fellow amateur astronomers, plus swap extra gear for new and exciting equipment from somebody else’s stash. Bring some food to share and any astronomy gear you’d like to sell, trade, or give away. We will have on hand some of the gear that was donated to the club this summer, including mirrors, lenses, blanks, telescope parts, and even entire telescopes. Come check out the bargains and visit with your fellow amateur astronomers in a relaxed evening before Christmas. We also encourage people to bring any new gear or projects they would like to show the rest of the club. The meeting is at 7:00 on December 22nd at EWEB’s Community Room, 500 E. 4th in Eugene. Next First Quarter Fridays: December 2nd and 30th Our November star party was clouded out, along with a good deal of the month afterward. If that sounds familiar, that’s because it is: I changed the date in the previous sentence from October to November and left the rest of the sentence intact. Yes, our autumn weather is predictable. Here’s hoping for a lucky break in the weather for our two December star parties. -

Another Unit of Distance (I Like This One Better): Light Year
How far away are the nearest stars? Last time: • Distances to stars can be measured via measurement of parallax (trigonometric parallax, stellar parallax) • Defined two units to be used in describing stellar distances (parsec and light year) Which stars are they? Another unit of distance (I like this A new unit of distance: the parsec one better): light year A parsec is the distance of a star whose parallax is 1 arcsecond. A light year is the distance a light ray travels in one year A star with a parallax of 1/2 arcsecond is at a distance of 2 parsecs. A light year is: • 9.460E+15 meters What is the parsec? • 3.26 light years = 1 parsec • 3.086 E+16 meters • 206,265 astronomical units The distances to the stars are truly So what are the distances to the stars? enormous • If the distance between the Earth and Sun were • First measurements made in 1838 (Friedrich Bessel) shrunk to 1 cm (0.4 inches), Alpha Centauri • Closest star is Alpha would be 2.75 km (1.7 miles) away Centauri, p=0.75 arcseconds, d=1.33 parsecs= 4.35 light years • Nearest stars are a few to many parsecs, 5 - 20 light years 1 When we look at the night sky, which So, who are our neighbors in space? are the nearest stars? Altair… 5.14 parsecs = 16.8 light years Look at Appendix 12 of the book (stars nearer than 4 parsecs or 13 light years) The nearest stars • 34 stars within 13 light years of the Sun • The 34 stars are contained in 25 star systems • Those visible to the naked eye are Alpha Centauri (A & B), Sirius, Epsilon Eridani, Epsilon Indi, Tau Ceti, and Procyon • We won’t see any of them tonight! Stars we can see with our eyes that are relatively close to the Sun A history of progress in measuring stellar distances • Arcturus … 36 light years • Parallaxes for even close stars • Vega … 26 light years are tiny and hard to measure • From Abell “Exploration of the • Altair … 17 light years Universe”, 1966: “For only about • Beta Canum Venaticorum . -

GEORGE HERBIG and Early Stellar Evolution
GEORGE HERBIG and Early Stellar Evolution Bo Reipurth Institute for Astronomy Special Publications No. 1 George Herbig in 1960 —————————————————————– GEORGE HERBIG and Early Stellar Evolution —————————————————————– Bo Reipurth Institute for Astronomy University of Hawaii at Manoa 640 North Aohoku Place Hilo, HI 96720 USA . Dedicated to Hannelore Herbig c 2016 by Bo Reipurth Version 1.0 – April 19, 2016 Cover Image: The HH 24 complex in the Lynds 1630 cloud in Orion was discov- ered by Herbig and Kuhi in 1963. This near-infrared HST image shows several collimated Herbig-Haro jets emanating from an embedded multiple system of T Tauri stars. Courtesy Space Telescope Science Institute. This book can be referenced as follows: Reipurth, B. 2016, http://ifa.hawaii.edu/SP1 i FOREWORD I first learned about George Herbig’s work when I was a teenager. I grew up in Denmark in the 1950s, a time when Europe was healing the wounds after the ravages of the Second World War. Already at the age of 7 I had fallen in love with astronomy, but information was very hard to come by in those days, so I scraped together what I could, mainly relying on the local library. At some point I was introduced to the magazine Sky and Telescope, and soon invested my pocket money in a subscription. Every month I would sit at our dining room table with a dictionary and work my way through the latest issue. In one issue I read about Herbig-Haro objects, and I was completely mesmerized that these objects could be signposts of the formation of stars, and I dreamt about some day being able to contribute to this field of study. -
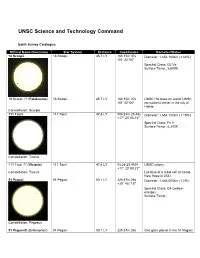
UNSC Science and Technology Command
UNSC Science and Technology Command Earth Survey Catalogue: Official Name/(Common) Star System Distance Coordinates Remarks/Status 18 Scorpii {TCP:p351} 18 Scorpii {Fact} 45.7 LY 16h 15m 37s Diameter: 1,654,100km (1.02R*) {Fact} -08° 22' 06" {Fact} Spectral Class: G2 Va {Fact} Surface Temp.: 5,800K {Fact} 18 Scorpii ?? (Falaknuma) 18 Scorpii {Fact} 45.7 LY 16h 15m 37s UNSC HQ base on world. UNSC {TCP:p351} {Fact} -08° 22' 06" recruitment center in the city of Halkia. {TCP:p355} Constellation: Scorpio 111 Tauri 111 Tauri {Fact} 47.8 LY 05h:24m:25.46s Diameter: 1,654,100km (1.19R*) {Fact} +17° 23' 00.72" {Fact} Spectral Class: F8 V {Fact} Surface Temp.: 6,200K {Fact} Constellation: Taurus 111 Tauri ?? (Victoria) 111 Tauri {Fact} 47.8 LY 05:24:25.4634 UNSC colony. {GoO:p31} {Fact} +17° 23' 00.72" Constellation: Taurus Location of a rebel cell at Camp New Hope in 2531. {GoO:p31} 51 Pegasi {Fact} 51 Pegasi {Fact} 50.1 LY 22h:57m:28s Diameter: 1,668,000km (1.2R*) {Fact} +20° 46' 7.8" {Fact} Spectral Class: G4 (yellow- orange) {Fact} Surface Temp.: Constellation: Pegasus 51 Pegasi-B (Bellerophon) 51 Pegasi 50.1 LY 22h:57m:28s Gas giant planet in the 51 Pegasi {Fact} +20° 46' 7.8" system informally named Bellerophon. Diameter: 196,000km. {Fact} Located on the edge of UNSC territory. {GoO:p15} Its moon, Pegasi Delta, contained a Covenant deuterium/tritium refinery destroyed by covert UNSC forces in 2545. {GoO:p13} Constellation: Pegasus 51 Pegasi-B-1 (Pegasi 51 Pegasi 50.1 LY 22h:57m:28s Moon of the gas giant planet 51 Delta) {GoO:p13} +20° 46' 7.8" Pegasi-B in the 51 Pegasi star Constellation: Pegasus system; a Covenant stronghold on the edge of UNSC territory. -

MAN-KZIN WARS V Created by Larry Niven with Jerry Pournelle S.M
MAN-KZIN WARS V Created by Larry Niven with Jerry Pournelle S.M. Stirling & Thomas T. Thomas MAN-KZIN WARS V This is a work of fiction. All the characters and events portrayed in this book are fictional, and any resemblance to real people or incidents is purely coincidental. Copyright ~ 1992, by Larry Niven All rights reserved, including the right to reproduce this book or portions thereof in any form. A Baen Books Original Baen Publishing Enterprises P.O. Box 1403 Riverdale, NY 10471 ISBN: 0-671-72137-2 Cover art by Stephen Hickman First Printing, October 1992 Printed in the United States of America Distributed by Simon & Schuster 1230 Avenue of the Americas New York, NY 10020 CONTENTS IN THE HALL OF THE MOUNTAIN KING, Jerry Pournelle & S.M. Stirling 7 HEY DIDDLE DIDDLE, Thomas T. Thomas 203 IN THE HALL OF THE MOUNTAIN KING Jerry Pournelle S.M. Sterling Copyright ~ 1992 by Jerry Pournelle & S.M. Stirling ù Prologue Durvash the tnuctipun knew he was dying. The thought did not bother him overmuch-he was a warrior of a peculiar and desperate kind and had never expected to survive the War-but the consciousness of failure was far worse than the wound along his side. Breath rasped harsh between his fangs. Thin fringed lips drew back from them, fledged with purple blood from his injured airsac. Unbending will kept all fourteen digits splayed on the rough rock; the light gravity of this world helped, as well. Cold wind hooted down from the heights, plucking at him until he came to a crack that was deep enough for a leg and an arm; the long flexible fingers on both wound into irregularities, anchoring him. -

Can We Communicate with an Alien Star System?
EXPLORATION 4: TO THE STARS! Can we communicate with an alien star system? The challenge ecently, astronomers have discovered more than 100 stars, in Raddition to our own Sun, that are orbited by planets! No one The solar system is our knows whether these alien star systems contain life. Sun plus all the planets, moons and other objects You have been asked by the United Nations to explore the that orbit it. possibility of traveling to one of these alien star systems. The U.N. A star system is a star also wants you to explore the possibility of communicating, from plus all the planets, Earth, with any life forms that might exist there. moons and other objects that orbit it. Your challenge is to use the telescope to determine the distance to one of these newly-discovered star systems. Using your findings, report on: How long would it take to reach the star and its planets by spaceship? Could we communicate with beings that might exist there? Artist's conception of planets orbiting another star. From the Ground Up!: Stars 1 © 2003 Smithsonian Institution Part 1. Your ideas about stars Suppose that the Earth were always cloudy at night, so that no one had ever seen the night sky. Would it make a difference to you? If so, how? _______________________________________________________ _______________________________________________________ _______________________________________________________ Do you think it's possible to travel to the stars? Would you want to go? If so, why? What would you expect / hope to find? _______________________________________________________ _______________________________________________________ _______________________________________________________ Describe some of the stories or movies you've seen in which humans travel between star systems. -
A Green Line Around the Box Means a Habitable Planet Exists in the Starsystem
Hussey 575 BD+30 2494 BD+24 2733 1.5 BD+14 2774 2.5 1.5 1.5 Ross 512 1.5 WO 9502 1.5 BD+17 2785 2 BD+15 3108 G136-101 Sigma Bootis BD+30 2512 1 Struve 1785 1.5 1 2.5 via LP441.33 1.5 BD+24 2786 1.5 1.5 1.5 1.5 1.5 45 Bootis L1344-37 GJ 3966 Ross 863 1.5 Lambda Serpentis Wolf 497 BD+25 2874 1.5 3 via V645 Herc Gliese 625 1 1.5 3.5 via GJ 3910 3 via V645 Herc 1.5 BD-9 3413 GJ-1179 Zeta Herculis 1.5 Eta Bootes 1 Rho Coronae Borealis 1.5 1.5 2.5 via Giclas 258.33 Luyten 758-105 BD+54 1716 1 BD+25 3173 Giclas 179-43 1.5 1.5 1.5 1 3 via Ross 948 3 via WO 9564 3 via GJ 3796 3 via Ross 948 Eta Coronae Borealis Chi Draconis 3 via HYG86887 1 3.5 via V645 Herc 1 Gamma Serpentis 2 BD+17 2611 (VESTA) Arcturus 3 via V645 Herc 3 via BD+21 2763 3.5 via BD+0 2989, DT Virginis 4 via HYG86887&8 Struve 2135 BD+33 2777 14 Herculis Porimma (Gamma Virginis) 3.5 via BD+45 2247 3 via BD+41 2695 1.5 3.5 BD+60 1623 BD+53 1719 THETIS 1.5 Chi Hercules 2 3.5 1.5 1.5 BD+38 3095 3.5 via BD+46 1189 Mu Herculis 4 via WO 9564 CR Draconis BD+52 2045 3 via BD+43 2796 1.5 3 via Giclas 179-43 BD+36 2393 Queen Isabel Star Sigma Draconis 3.5 via BD+43 2796 CE Bootes 1.5 BD+19 2881 1 1.5 1.5 1.5 2.5 I Bootis via BD+45 2247 BD+47 2112 1 4 via EGWD 329, CR Draconis 3 via LP 272-25 4.5 via Ross 948, L 910-10 44 Bootis Aitkens Double Star 1 ADS 10288 3 via BD+61 2068 1.5 Gilese 625 1.5 Vega 3 via Kuiper 79 3 via Giclas 179-43 4 via BD+46 1189, BD+50 2030 Ross 52 Theta Draconis 2 EV Lacertae Gliese 892 BD+39 2947 3 via BD+18 3421 1.5 0.5 Theta Bootis 1.5 3 via EV Lacertae 2.5 via -

Serpens – the Serpent
A JPL Image of surface of Mars, and JPL Ingenuity Helicioptor illustration, in flight Monthly Meeting May 10th at 7:00 PM at HRPO, and via Jitsi (Monthly meetings are on 2nd Mondays at Highland Road Park Observatory, will also broadcast via. (meet.jit.si/BRASMeet). PRESENTATION: Dr. Alan Hale, professional astronomer and co-discoverer of Comet Hale-Bopp, among other endeavors. What's In This Issue? President’s Message Member Meeting Minutes Business Meeting Minutes Outreach Report Light Pollution Committee Report Globe at Night SubReddit and Discord Messages from the HRPO REMOTE DISCUSSION Solar Viewing International Astronomy Day American Radio Relay League Field Day Observing Notes: Serpens - The Serpent & Mythology Like this newsletter? See PAST ISSUES online back to 2009 Visit us on Facebook – Baton Rouge Astronomical Society BRAS YouTube Channel Baton Rouge Astronomical Society Newsletter, Night Visions Page 2 of 20 May 2021 President’s Message Ahhh, welcome to May, the last pleasant month in Louisiana before the start of the hurricane season and the brutal summer months that follow. April flew by pretty quickly, and with the world slowly thawing from the long winter, why shouldn’t it? To celebrate, we decided we’re going to try to start holding our monthly meetings at Highland Road Park Observatory again, only with the added twist of incorporating an on-line component for those who for whatever reason don’t feel like making it out. To that end, we’ll have both our usual live broadcast on the BRAS YouTube channel and the Brasmeet page on Jitsi—which is where our out of town guests and, at least this month, our guest speaker can join us. -
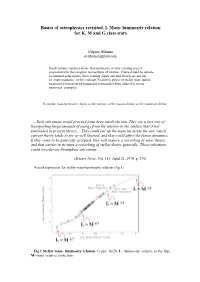
Basics of Astrophysics Revisited. I. Mass- Luminosity Relation for K, M and G Class Stars
Basics of astrophysics revisited. I. Mass- luminosity relation for K, M and G class stars Edgars Alksnis [email protected] Small volume statistics show, that luminosity of slow rotating stars is proportional to their angular momentums of rotation. Cause should be outside of standard solar model. Slow rotating giants and dim dwarfs are not out of „main sequence” in this concept. Predictive power of stellar mass-radius- equatorial rotation speed-luminosity relation has been offered to test in numerous examples. Keywords: mass-luminosity relation, stellar rotation, stellar mass prediction, stellar rotation prediction ...Such vibrations would proceed from deep inside the sun. They are a fast way of transporting large amounts of energy from the interior to the surface that is not envisioned in present theory.... They could stir up the material inside the sun, which current theory tends to see as well layered, and that could affect the fusion dynamics. If they come to be generally accepted, they will require a reworking of solar theory, and that carries in its train a reworking of stellar theory generally. These vibrations could reverberate throughout astronomy. (Science News, Vol. 115, April 21, 1979, p. 270). Actual expression for stellar mass-luminosity relation (fig.1) Fig.1 Stellar mass- luminosity relation. Credit: Ay20. L- luminosity, relative to the Sun, M- mass, relative to the Sun. remain empiric and in fact contain unresolvable contradiction: stellar luminosity basically is connected with their surface area (radius squared) but mass (radius in cube) appears as a factor which generate luminosity. That purely geometric difference had pressed astrophysicists to place several classes of stars outside of „main sequence” in the frame of their strange theoretic constructions. -
5-6Index 6 MB
CLEAR SKIES OBSERVING GUIDES 5-6" Carbon Stars 228 Open Clusters 751 Globular Clusters 161 Nebulae 199 Dark Nebulae 139 Planetary Nebulae 105 Supernova Remnants 10 Galaxies 693 Asterisms 65 Other 4 Clear Skies Observing Guides - ©V.A. van Wulfen - clearskies.eu - [email protected] Index ANDROMEDA - the Princess ST Andromedae And CS SU Andromedae And CS VX Andromedae And CS AQ Andromedae And CS CGCS135 And CS UY Andromedae And CS NGC7686 And OC Alessi 22 And OC NGC752 And OC NGC956 And OC NGC7662 - "Blue Snowball Nebula" And PN NGC7640 And Gx NGC404 - "Mirach's Ghost" And Gx NGC891 - "Silver Sliver Galaxy" And Gx Messier 31 (NGC224) - "Andromeda Galaxy" And Gx Messier 32 (NGC221) And Gx Messier 110 (NGC205) And Gx "Golf Putter" And Ast ANTLIA - the Air Pump AB Antliae Ant CS U Antliae Ant CS Turner 5 Ant OC ESO435-09 Ant OC NGC2997 Ant Gx NGC3001 Ant Gx NGC3038 Ant Gx NGC3175 Ant Gx NGC3223 Ant Gx NGC3250 Ant Gx NGC3258 Ant Gx NGC3268 Ant Gx NGC3271 Ant Gx NGC3275 Ant Gx NGC3281 Ant Gx Streicher 8 - "Parabola" Ant Ast APUS - the Bird of Paradise U Apodis Aps CS IC4499 Aps GC NGC6101 Aps GC Henize 2-105 Aps PN Henize 2-131 Aps PN AQUARIUS - the Water Bearer Messier 72 (NGC6981) Aqr GC Messier 2 (NGC7089) Aqr GC NGC7492 Aqr GC NGC7009 - "Saturn Nebula" Aqr PN NGC7293 - "Helix Nebula" Aqr PN NGC7184 Aqr Gx NGC7377 Aqr Gx NGC7392 Aqr Gx NGC7585 (Arp 223) Aqr Gx NGC7606 Aqr Gx NGC7721 Aqr Gx NGC7727 (Arp 222) Aqr Gx NGC7723 Aqr Gx Messier 73 (NGC6994) Aqr Ast 14 Aquarii Group Aqr Ast 5-6" V2.4 Clear Skies Observing Guides - ©V.A. -

Serpentis System Information
SERPENTIS SYSTEM INFORMATION Primary: Lambda Serpentis • Class: G0-V main sequence star Lambda Serpentis IIB • Mass: 1.04 Solar Masses (2.06 x 1030 kg) • Mean orbital distance: 825,000 km • Radius: 1.1 • Diameter: 4,960 km • Magnitude: 4.4 • Density: 4.741 x 103 kg/m3 • Luminosity: 1.04 • Mass: 3.03 x 1023 kg • Gravity: 0.336 g Lambda Serpentis I • Orbital period: 78.4 Standard Days • Mean orbital distance: 0.7 AU (105 million km) • Rotational period: 29.5 Standard Days • Diameter: 12,141 km • Avg. surface pressure: 0.14 atm • Mass: 5 x 1024 kg • Avg. mean temp: 29°C • Orbital Period: 210 Standard Days Lambda Serpentis III Lambda Serpentis II • Orbital distance: 1.4 to 1.8 AU (210 million km • Mean orbital distance: 1.1 AU (165 million km) to 270 million km) • Diameter: 13,750 km • Circumferance: 43,121 km Lambda Serpentis IV • Axial tilt: 29°05' 57" • Mean orbital distance: 2.3 AU (345 million km) • Rotation: 30.012 Standard Hours • Diameter: 42,960 km • Year: 413.2 Standard Days • Mass: 6.6 x 1025 kg • Mass: 1.133 Earth Masses (6.799 x 1024 kg) • Orbital Period: 1,259 Standard Days • Density: 4.999 x 103 kg/m3 • Gravity: 0.98 g Lambda Serpentis V • Albedo: 0.74 • Mean orbital distance: 3.5 AU (525 million km) • Avg. surface pressure: 1.30 atm • Diameter: 112,440 km • Dry surface area: 3% • Mass: 6.4 x 1026 kg • Avg. cloud cover: 70% • Orbital Period: 6.42 Standard Years • Avg. mean temp: 19°C Lambda Serpentis VI Lambda Serpentis IIA • Mean orbital distance: 5.5 AU (825 million km) • Mean orbital distance: 587,400 km • Diameter: 50,000 km • Diameter: 7,243 km • Mass: 1.1 x 1026 kg • Density: 4.941 x 103 kg/m3 • Orbital Period: 12.65 Standard Years • Mass: 9.827 x 1023 kg • Gravity: 0.510 g • Orbital period: 47 Standard Days • Rotational period: 46.9 Standard Days • Avg. -

Spitzer Approved Galactic Spitzer Approved Galactic
Printed_by_SSC Mar 25, 10 16:33Spitzer_Approved_Galactic Page 1/847 Mar 25, 10 16:33Spitzer_Approved_Galactic Page 2/847 Spitzer Space Telescope − Archive Research Proposal #20309 Spitzer Space Telescope − Archive Research Proposal #30144 PAH Emission Features in the 15 to 20 Micron Region: Emitting to the Beat of a Diamonds are a PAHs Best Friend Different Drummer Principal Investigator: Louis Allamandola Principal Investigator: Louis Allamandola Institution: NASA Ames Research Center Institution: NASA Ames Research Center Technical Contact: Louis Allamandola, NASA Ames Research Center Technical Contact: Louis Allamandola, NASA Ames Research Center Co−Investigators: Co−Investigators: Andrew Mattioda, SETI Andrew Mattioda, SETI Institute and NASA Ames Els Peeters, SETI Els Peeters, NASA Ames Research Center Douglas Hudgins, NASA Ames Research Center Douglas Hudgins, NASA Ames Research Center Alexander Tielens, NASA Ames Research Center Xander Tielens, Kapteyn Institute, The Netherlands Charles Bauschlicher, Jr., NASA Ames Research Center Charlie Bauschlicher, Jr., NASA Ames Research Center Science Category: ISM Science Category: ISM Dollars Approved: 56727.0 Dollars Approved: 72000.0 Abstract: Abstract: The mid−IR spectroscopic capabilities and unprecedented sensitivity of the Spitzer has added a new complex of bands near 17 um to the PAH emission band Spitzer Space Telescope has shown that the ubiquitious infrared (IR) emission family. This 17 um band complex, the second most intense of the PAH features, features can be used as probes of many galactic and extragalactic objects. carries unique information about the emitting species. Because these bands arise These features, formerly called the Unidentified Infrared (UIR) Bands, are now from drumhead vibrations of the hexagonal carbon skeleton, they carry generally attributed to the vibrational emission from polycyclic aromatic information directly related to PAH shape, size, and charge.