Euclid's Elements: Introduction to “Proofs” Euclid Is
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Canada Archives Canada Published Heritage Direction Du Branch Patrimoine De I'edition
Rhetoric more geometrico in Proclus' Elements of Theology and Boethius' De Hebdomadibus A Thesis submitted in Candidacy for the Degree of Master of Arts in Philosophy Institute for Christian Studies Toronto, Ontario By Carlos R. Bovell November 2007 Library and Bibliotheque et 1*1 Archives Canada Archives Canada Published Heritage Direction du Branch Patrimoine de I'edition 395 Wellington Street 395, rue Wellington Ottawa ON K1A0N4 Ottawa ON K1A0N4 Canada Canada Your file Votre reference ISBN: 978-0-494-43117-7 Our file Notre reference ISBN: 978-0-494-43117-7 NOTICE: AVIS: The author has granted a non L'auteur a accorde une licence non exclusive exclusive license allowing Library permettant a la Bibliotheque et Archives and Archives Canada to reproduce, Canada de reproduire, publier, archiver, publish, archive, preserve, conserve, sauvegarder, conserver, transmettre au public communicate to the public by par telecommunication ou par Plntemet, prefer, telecommunication or on the Internet, distribuer et vendre des theses partout dans loan, distribute and sell theses le monde, a des fins commerciales ou autres, worldwide, for commercial or non sur support microforme, papier, electronique commercial purposes, in microform, et/ou autres formats. paper, electronic and/or any other formats. The author retains copyright L'auteur conserve la propriete du droit d'auteur ownership and moral rights in et des droits moraux qui protege cette these. this thesis. Neither the thesis Ni la these ni des extraits substantiels de nor substantial extracts from it celle-ci ne doivent etre imprimes ou autrement may be printed or otherwise reproduits sans son autorisation. reproduced without the author's permission. -

Thermodynamics of Spacetime: the Einstein Equation of State
gr-qc/9504004 UMDGR-95-114 Thermodynamics of Spacetime: The Einstein Equation of State Ted Jacobson Department of Physics, University of Maryland College Park, MD 20742-4111, USA [email protected] Abstract The Einstein equation is derived from the proportionality of entropy and horizon area together with the fundamental relation δQ = T dS connecting heat, entropy, and temperature. The key idea is to demand that this relation hold for all the local Rindler causal horizons through each spacetime point, with δQ and T interpreted as the energy flux and Unruh temperature seen by an accelerated observer just inside the horizon. This requires that gravitational lensing by matter energy distorts the causal structure of spacetime in just such a way that the Einstein equation holds. Viewed in this way, the Einstein equation is an equation of state. This perspective suggests that it may be no more appropriate to canonically quantize the Einstein equation than it would be to quantize the wave equation for sound in air. arXiv:gr-qc/9504004v2 6 Jun 1995 The four laws of black hole mechanics, which are analogous to those of thermodynamics, were originally derived from the classical Einstein equation[1]. With the discovery of the quantum Hawking radiation[2], it became clear that the analogy is in fact an identity. How did classical General Relativity know that horizon area would turn out to be a form of entropy, and that surface gravity is a temperature? In this letter I will answer that question by turning the logic around and deriving the Einstein equation from the propor- tionality of entropy and horizon area together with the fundamental relation δQ = T dS connecting heat Q, entropy S, and temperature T . -

Chapter 5 Dimensional Analysis and Similarity
Chapter 5 Dimensional Analysis and Similarity Motivation. In this chapter we discuss the planning, presentation, and interpretation of experimental data. We shall try to convince you that such data are best presented in dimensionless form. Experiments which might result in tables of output, or even mul- tiple volumes of tables, might be reduced to a single set of curves—or even a single curve—when suitably nondimensionalized. The technique for doing this is dimensional analysis. Chapter 3 presented gross control-volume balances of mass, momentum, and en- ergy which led to estimates of global parameters: mass flow, force, torque, total heat transfer. Chapter 4 presented infinitesimal balances which led to the basic partial dif- ferential equations of fluid flow and some particular solutions. These two chapters cov- ered analytical techniques, which are limited to fairly simple geometries and well- defined boundary conditions. Probably one-third of fluid-flow problems can be attacked in this analytical or theoretical manner. The other two-thirds of all fluid problems are too complex, both geometrically and physically, to be solved analytically. They must be tested by experiment. Their behav- ior is reported as experimental data. Such data are much more useful if they are ex- pressed in compact, economic form. Graphs are especially useful, since tabulated data cannot be absorbed, nor can the trends and rates of change be observed, by most en- gineering eyes. These are the motivations for dimensional analysis. The technique is traditional in fluid mechanics and is useful in all engineering and physical sciences, with notable uses also seen in the biological and social sciences. -
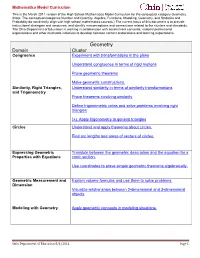
High School Geometry Model Curriculum Math.Pdf
Mathematics Model Curriculum This is the March 2011 version of the High School Mathematics Model Curriculum for the conceptual category Geometry. (Note: The conceptual categories Number and Quantity, Algebra, Functions, Modeling, Geometry, and Statistics and Probability do not directly align with high school mathematics courses.) The current focus of this document is to provide instructional strategies and resources, and identify misconceptions and connections related to the clusters and standards. The Ohio Department of Education is working in collaboration with assessment consortia, national professional organizations and other multistate initiatives to develop common content elaborations and learning expectations. Geometry Domain Cluster Congruence Experiment with transformations in the plane Understand congruence in terms of rigid motions Prove geometric theorems Make geometric constructions. Similarity, Right Triangles, Understand similarity in terms of similarity transformations and Trigonometry Prove theorems involving similarity Define trigonometric ratios and solve problems involving right triangles (+) Apply trigonometry to general triangles Circles Understand and apply theorems about circles. Find arc lengths and areas of sectors of circles. Expressing Geometric Translate between the geometric description and the equation for a Properties with Equations conic section. Use coordinates to prove simple geometric theorems algebraically. Geometric Measurement and Explain volume formulas and use them to solve problems. Dimension -

Circle Theorems
Circle theorems A LEVEL LINKS Scheme of work: 2b. Circles – equation of a circle, geometric problems on a grid Key points • A chord is a straight line joining two points on the circumference of a circle. So AB is a chord. • A tangent is a straight line that touches the circumference of a circle at only one point. The angle between a tangent and the radius is 90°. • Two tangents on a circle that meet at a point outside the circle are equal in length. So AC = BC. • The angle in a semicircle is a right angle. So angle ABC = 90°. • When two angles are subtended by the same arc, the angle at the centre of a circle is twice the angle at the circumference. So angle AOB = 2 × angle ACB. • Angles subtended by the same arc at the circumference are equal. This means that angles in the same segment are equal. So angle ACB = angle ADB and angle CAD = angle CBD. • A cyclic quadrilateral is a quadrilateral with all four vertices on the circumference of a circle. Opposite angles in a cyclic quadrilateral total 180°. So x + y = 180° and p + q = 180°. • The angle between a tangent and chord is equal to the angle in the alternate segment, this is known as the alternate segment theorem. So angle BAT = angle ACB. Examples Example 1 Work out the size of each angle marked with a letter. Give reasons for your answers. Angle a = 360° − 92° 1 The angles in a full turn total 360°. = 268° as the angles in a full turn total 360°. -

Lesson 19: Equations for Tangent Lines to Circles
NYS COMMON CORE MATHEMATICS CURRICULUM Lesson 19 M5 GEOMETRY Lesson 19: Equations for Tangent Lines to Circles Student Outcomes . Given a circle, students find the equations of two lines tangent to the circle with specified slopes. Given a circle and a point outside the circle, students find the equation of the line tangent to the circle from that point. Lesson Notes This lesson builds on the understanding of equations of circles in Lessons 17 and 18 and on the understanding of tangent lines developed in Lesson 11. Further, the work in this lesson relies on knowledge from Module 4 related to G-GPE.B.4 and G-GPE.B.5. Specifically, students must be able to show that a particular point lies on a circle, compute the slope of a line, and derive the equation of a line that is perpendicular to a radius. The goal is for students to understand how to find equations for both lines with the same slope tangent to a given circle and to find the equation for a line tangent to a given circle from a point outside the circle. Classwork Opening Exercise (5 minutes) Students are guided to determine the equation of a line perpendicular to a chord of a given circle. Opening Exercise A circle of radius ퟓ passes through points 푨(−ퟑ, ퟑ) and 푩(ퟑ, ퟏ). a. What is the special name for segment 푨푩? Segment 푨푩 is called a chord. b. How many circles can be drawn that meet the given criteria? Explain how you know. Scaffolding: Two circles of radius ퟓ pass through points 푨 and 푩. -

Can One Design a Geometry Engine? on the (Un) Decidability of Affine
Noname manuscript No. (will be inserted by the editor) Can one design a geometry engine? On the (un)decidability of certain affine Euclidean geometries Johann A. Makowsky Received: June 4, 2018/ Accepted: date Abstract We survey the status of decidabilty of the consequence relation in various ax- iomatizations of Euclidean geometry. We draw attention to a widely overlooked result by Martin Ziegler from 1980, which proves Tarski’s conjecture on the undecidability of finitely axiomatizable theories of fields. We elaborate on how to use Ziegler’s theorem to show that the consequence relations for the first order theory of the Hilbert plane and the Euclidean plane are undecidable. As new results we add: (A) The first order consequence relations for Wu’s orthogonal and metric geometries (Wen- Ts¨un Wu, 1984), and for the axiomatization of Origami geometry (J. Justin 1986, H. Huzita 1991) are undecidable. It was already known that the universal theory of Hilbert planes and Wu’s orthogonal geom- etry is decidable. We show here using elementary model theoretic tools that (B) the universal first order consequences of any geometric theory T of Pappian planes which is consistent with the analytic geometry of the reals is decidable. The techniques used were all known to experts in mathematical logic and geometry in the past but no detailed proofs are easily accessible for practitioners of symbolic computation or automated theorem proving. Keywords Euclidean Geometry · Automated Theorem Proving · Undecidability arXiv:1712.07474v3 [cs.SC] 1 Jun 2018 J.A. Makowsky Faculty of Computer Science, Technion–Israel Institute of Technology, Haifa, Israel E-mail: [email protected] 2 J.A. -
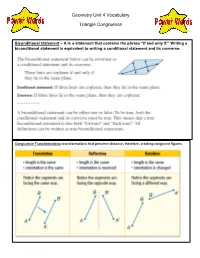
Geometry Unit 4 Vocabulary Triangle Congruence
Geometry Unit 4 Vocabulary Triangle Congruence Biconditional statement – A is a statement that contains the phrase “if and only if.” Writing a biconditional statement is equivalent to writing a conditional statement and its converse. Congruence Transformations–transformations that preserve distance, therefore, creating congruent figures Congruence – the same shape and the same size Corresponding Parts of Congruent Triangles are Congruent CPCTC – the angle made by two lines with a common vertex. (When two lines meet at a common point Included angle (vertex) the angle between them is called the included angle. The two lines define the angle.) Included side – the common side of two legs. (Usually found in triangles and other polygons, the included side is the one that links two angles together. Think of it as being “included” between 2 angles. Overlapping triangles – triangles lying on top of one another sharing some but not all sides. Theorems AAS Congruence Theorem – Triangles are congruent if two pairs of corresponding angles and a pair of opposite sides are equal in both triangles. ASA Congruence Theorem -Triangles are congruent if any two angles and their included side are equal in both triangles. SAS Congruence Theorem -Triangles are congruent if any pair of corresponding sides and their included angles are equal in both triangles. SAS SSS Congruence Theorem -Triangles are congruent if all three sides in one triangle are congruent to the corresponding sides in the other. Special congruence theorem for RIGHT TRIANGLES! . -

A Congruence Problem for Polyhedra
A congruence problem for polyhedra Alexander Borisov, Mark Dickinson, Stuart Hastings April 18, 2007 Abstract It is well known that to determine a triangle up to congruence requires 3 measurements: three sides, two sides and the included angle, or one side and two angles. We consider various generalizations of this fact to two and three dimensions. In particular we consider the following question: given a convex polyhedron P , how many measurements are required to determine P up to congruence? We show that in general the answer is that the number of measurements required is equal to the number of edges of the polyhedron. However, for many polyhedra fewer measurements suffice; in the case of the cube we show that nine carefully chosen measurements are enough. We also prove a number of analogous results for planar polygons. In particular we describe a variety of quadrilaterals, including all rhombi and all rectangles, that can be determined up to congruence with only four measurements, and we prove the existence of n-gons requiring only n measurements. Finally, we show that one cannot do better: for any ordered set of n distinct points in the plane one needs at least n measurements to determine this set up to congruence. An appendix by David Allwright shows that the set of twelve face-diagonals of the cube fails to determine the cube up to conjugacy. Allwright gives a classification of all hexahedra with all face- diagonals of equal length. 1 Introduction We discuss a class of problems about the congruence or similarity of three dimensional polyhedra. -

Angles ANGLE Topics • Coterminal Angles • Defintion of an Angle
Angles ANGLE Topics • Coterminal Angles • Defintion of an angle • Decimal degrees to degrees, minutes, seconds by hand using the TI-82 or TI-83 Plus • Degrees, seconds, minutes changed to decimal degree by hand using the TI-82 or TI-83 Plus • Standard position of an angle • Positive and Negative angles ___________________________________________________________________________ Definition: Angle An angle is created when a half-ray (the initial side of the angle) is drawn out of a single point (the vertex of the angle) and the ray is rotated around the point to another location (becoming the terminal side of the angle). An angle is created when a half-ray (initial side of angle) A: vertex point of angle is drawn out of a single point (vertex) AB: Initial side of angle. and the ray is rotated around the point to AC: Terminal side of angle another location (becoming the terminal side of the angle). Hence angle A is created (also called angle BAC) STANDARD POSITION An angle is in "standard position" when the vertex is at the origin and the initial side of the angle is along the positive x-axis. Recall: polynomials in algebra have a standard form (all the terms have to be listed with the term having the highest exponent first). In trigonometry, there is a standard position for angles. In this way, we are all talking about the same thing and are not trying to guess if your math solution and my math solution are the same. Not standard position. Not standard position. This IS standard position. Initial side not along Initial side along negative Initial side IS along the positive x-axis. -

20. Geometry of the Circle (SC)
20. GEOMETRY OF THE CIRCLE PARTS OF THE CIRCLE Segments When we speak of a circle we may be referring to the plane figure itself or the boundary of the shape, called the circumference. In solving problems involving the circle, we must be familiar with several theorems. In order to understand these theorems, we review the names given to parts of a circle. Diameter and chord The region that is encompassed between an arc and a chord is called a segment. The region between the chord and the minor arc is called the minor segment. The region between the chord and the major arc is called the major segment. If the chord is a diameter, then both segments are equal and are called semi-circles. The straight line joining any two points on the circle is called a chord. Sectors A diameter is a chord that passes through the center of the circle. It is, therefore, the longest possible chord of a circle. In the diagram, O is the center of the circle, AB is a diameter and PQ is also a chord. Arcs The region that is enclosed by any two radii and an arc is called a sector. If the region is bounded by the two radii and a minor arc, then it is called the minor sector. www.faspassmaths.comIf the region is bounded by two radii and the major arc, it is called the major sector. An arc of a circle is the part of the circumference of the circle that is cut off by a chord. -

Understand the Principles and Properties of Axiomatic (Synthetic
Michael Bonomi Understand the principles and properties of axiomatic (synthetic) geometries (0016) Euclidean Geometry: To understand this part of the CST I decided to start off with the geometry we know the most and that is Euclidean: − Euclidean geometry is a geometry that is based on axioms and postulates − Axioms are accepted assumptions without proofs − In Euclidean geometry there are 5 axioms which the rest of geometry is based on − Everybody had no problems with them except for the 5 axiom the parallel postulate − This axiom was that there is only one unique line through a point that is parallel to another line − Most of the geometry can be proven without the parallel postulate − If you do not assume this postulate, then you can only prove that the angle measurements of right triangle are ≤ 180° Hyperbolic Geometry: − We will look at the Poincare model − This model consists of points on the interior of a circle with a radius of one − The lines consist of arcs and intersect our circle at 90° − Angles are defined by angles between the tangent lines drawn between the curves at the point of intersection − If two lines do not intersect within the circle, then they are parallel − Two points on a line in hyperbolic geometry is a line segment − The angle measure of a triangle in hyperbolic geometry < 180° Projective Geometry: − This is the geometry that deals with projecting images from one plane to another this can be like projecting a shadow − This picture shows the basics of Projective geometry − The geometry does not preserve length