Impact of a Blended ICT Adoption Model on Chilean Vulnerable Schools Correlates with Amount of on Online Practice
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Primer Tribunal Electoral De La Region Metropolitana
PRIMER TRIBUNAL ELECTORAL DE LA REGIÓN METROPOLITANA ESTADO CONFORME AL ART. 27 LEY N° 18.593 Pág.1/3 Santiago, 11 de octubre de 2018 ORDEN ROL N° ROL (en letras) RECLAMANTE - MATERIA RESOLUCIONES 1 6224 Seis mil doscientos veinticuatro Junta de Vecinos “Amapolas” de la comuna de Ñuñoa. Calificación elecciones. Sentencia 2 6321 Seis mil trescientos veintiuno CDL de Salud “Cesfam Quinta Bella” de la comuna de Recoleta. Calificación elecciones. Sentencia 3 6375 Seis mil trescientos setenta y cinco Club Deportivo “Fernando Collinao” de la comuna de Lo Prado. Calificación elecciones. Sentencia 4 6458 Seis mil cuatrocientos cincuenta y ocho Club de Adulto Mayor “Comienzo de una Vida” de la comuna de La Cisterna. Calificación elecciones. Sentencia Club Deportivo y Social “Seniors Villa España” de la comuna de Estación Central. Calificación 5 6463 Seis mil cuatrocientos sesenta y tres elecciones Sentencia 6 6465 Seis mil cuatrocientos sesenta y cinco Comité de Allegados “Juntos por Nuestra Casa” de la comuna de La Granja. Calificación elecciones. Sentencia Club Adulto Mayor, Cultural y Social “Los Años Dorados” de la comuna de Huechuraba. Calificación 7 6466 Seis mil cuatrocientos sesenta y seis elecciones. Sentencia 8 6468 Seis mil cuatrocientos sesenta y ocho Centro Cultural “Comunicacional TV 8 Peñalolén” de la comuna de Peñalolén. Calificación elecciones. Sentencia 9 6473 Seis mil cuatrocientos setenta y tres Club del Adulto Mayor “Pila del Ganso” de la comuna de Estación Central. Calificación elecciones. Sentencia Centro de Desarrollo Social “Esperanza del Mañana” de la comuna de La Granja. Calificación 10 6503 Seis mil quinientos tres elecciones. Sentencia 11 6607 Seis mil seiscientos siete Comité de Allegados “Fuerza y Coraje” de la comuna de Puente Alto. -
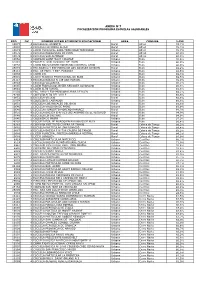
Rbd Dv Nombre Establecimiento
ANEXO N°7 FOCALIZACIÓN PROGRAMA ESCUELAS SALUDABLES RBD DV NOMBRE ESTABLECIMIENTO EDUCACIONAL AREA COMUNA %IVE 10877 4 ESCUELA EL ASIENTO Rural Alhué 74,7% 10880 4 ESCUELA HACIENDA ALHUE Rural Alhué 78,3% 10873 1 LICEO MUNICIPAL SARA TRONCOSO TRONCOSO Urbano Alhué 78,7% 10878 2 ESCUELA BARRANCAS DE PICHI Rural Alhué 80,0% 10879 0 ESCUELA SAN ALFONSO Rural Alhué 90,3% 10662 3 COLEGIO SAINT MARY COLLEGE Urbano Buin 76,5% 31081 6 ESCUELA SAN IGNACIO DE BUIN Urbano Buin 86,0% 10658 5 LICEO POLIVALENTE MODERNO CARDENAL CARO Urbano Buin 86,0% 26015 0 ESC.BASICA Y ESP.MARIA DE LOS ANGELES DE BUIN Rural Buin 88,2% 26111 4 ESC. DE PARV. Y ESP. PUKARAY Urbano Buin 88,6% 10638 0 LICEO 131 Urbano Buin 89,3% 25591 2 LICEO TECNICO PROFESIONAL DE BUIN Urbano Buin 89,5% 26117 3 ESCUELA BÁSICA N 149 SAN MARCEL Urbano Buin 89,9% 10643 7 ESCUELA VILLASECA Urbano Buin 90,1% 10645 3 LICEO FRANCISCO JAVIER KRUGGER ALVARADO Urbano Buin 90,8% 10641 0 LICEO ALTO JAHUEL Urbano Buin 91,8% 31036 0 ESC. PARV.Y ESP MUNDOPALABRA DE BUIN Urbano Buin 92,1% 26269 2 COLEGIO ALTO DEL VALLE Urbano Buin 92,5% 10652 6 ESCUELA VILUCO Rural Buin 92,6% 31054 9 COLEGIO EL LABRADOR Urbano Buin 93,6% 10651 8 ESCUELA LOS ROSALES DEL BAJO Rural Buin 93,8% 10646 1 ESCUELA VALDIVIA DE PAINE Urbano Buin 93,9% 10649 6 ESCUELA HUMBERTO MORENO RAMIREZ Rural Buin 94,3% 10656 9 ESCUELA BASICA G-N°813 LOS AROMOS DE EL RECURSO Rural Buin 94,9% 10648 8 ESCUELA LO SALINAS Rural Buin 94,9% 10640 2 COLEGIO DE MAIPO Urbano Buin 97,9% 26202 1 ESCUELA ESP. -

13 Anexo N°13 Focalizacion
ANEXO N°13 NOMINA DE ESTABLECIMIENTOS EDUCACIONALES FOCALIZADOS RBD DV Nombre establecimiento Comuna IVE SINAE Observación 9088 3 LICEO ANTONIO HERMIDA FABRES Peñalolén 91,15% CONTINUIDAD 9098 0 ESCUELA JUAN BAUTISTA PASTEN Peñalolén 89,77% CONTINUIDAD 9103 0 ESCUELA UNION NACIONAL ARABE Peñalolén 85,03% CONTINUIDAD 9105 7 CENTRO EDUCACIONAL EDUARDO DE LA BARRA Peñalolén 91,26% CONTINUIDAD 24997 1 ESCUELA SANTA MARIA DE PENALOLEN Peñalolén 91,57% CONTINUIDAD 10455 8 LICEO SAN GERONIMO Puente Alto 90,70% CONTINUIDAD 10458 2 ESCUELA VILLA INDEPENDENCIA Puente Alto 93,03% CONTINUIDAD 10461 2 ESCUELA LOS ANDES Puente Alto 88,08% CONTINUIDAD 10464 7 ESCUELA VILLA PEDRO AGUIRRE CERDA Puente Alto 90,57% CONTINUIDAD 10465 5 ESCUELA EJERCITO LIBERTADOR Puente Alto 94,28% CONTINUIDAD 10472 8 ESCUELA CASAS VIEJAS Puente Alto 86,40% CONTINUIDAD 10476 0 ESCUELA LAS PALMAS Puente Alto 93,00% CONTINUIDAD 24443 0 LICEO MUNICIPAL CHILOE Puente Alto 94,03% CONTINUIDAD 24987 4 ESCUELA ANDES DEL SUR Puente Alto 82,13% CONTINUIDAD 25002 3 ESCUELA BASICA PADRE ALBERTO HURTADO Puente Alto 95,13% CONTINUIDAD 9863 9 LICEO SANTIAGO BUERAS Y AVARIA Maipú 75,76% CONTINUIDAD 9867 1 CENTRO DE EDUC. TECN.PROFESIONAL CODEDUC Maipú 81,33% CONTINUIDAD 9892 2 ESCUELA LAS AMERICAS Maipú 66,87% CONTINUIDAD 24883 5 ESCUELA BÁSICA MUNICIPAL SAN LUIS Maipú 92,62% CONTINUIDAD 25314 6 ESCUELA BÁSICA 1737 LOS ALERCES DE MAIPÚ Maipú 79,89% CONTINUIDAD 9778 7 ESCUELA BASICA GERMAN RIESCO ERRAZURIZ Maipú 79,65% CONTINUIDAD 9881 7 ESCUELA VICENTE REYES PALAZUELOS Maipú 85,71% CONTINUIDAD 9883 3 ESCUELA BÁSICA N 263 RAMON FREIRE Maipú 85,59% CONTINUIDAD 9889 2 LICEO REINO DE DINAMARCA Maipú 89,94% CONTINUIDAD 9895 7 ESCUELA BASICA REINA DE SUECIA Maipú 77,76% CONTINUIDAD 25186 0 COLEGIO MUNIC. -

Sostenibilidad Urbana En La Comuna De Santiago De Chile
AE-OBSV. Observatorios de Sostenibilidad. Iniciativas Españolas e Iberoamericanas SOSTENIBILIDAD URBANA EN LA COMUNA DE SANTIAGO DE CHILE Néstor Ahumada Galaz Técnico Asesoría Urbana ASESORÍA URBANA MUNICIPALIDAD DE SANTIAGO DE CHILE www.conama9.org Sostenibilidad Urbana en la Comuna de Santiago de Chile Néstor Ahumada Galaz Geógrafo I. Municipalidad de Santiago Asesoría Urbana Santiago en el continente Región Metropolitana en el contexto nacional Chile en el Contexto Sudamericano Superficie continental: 816.260 Km2 Capital: Santiago, ubicada en la Región Metropolitana Superficie territorio antártico: 1.250.000 km2 Población: 15.116.435 de habitantes (aprox.) Superficie Región Metropolitana: 15.403 km2 Regiones: 13 Población de la ciudad de Santiago (R M): 6.061.185. Santiago Metropolitano Evolución 1541 1600 1900 1920 1940 1952 1960 1970 1980 1996 2004 Antecedentes generales 2005 COMUNA DE SANTIAGO Superficie : 2.320 há. QU ILI CU RA HUECHURABA VI TAC URA Población : 200.792 hab. CONCHALI RENCA Densidad : 99.5 hab/há. RECOLETA LAS CONDES INDEPENDENCIA CERRO NAVIA Población flotante: 1.800.000 QUINTA NORMAL PR OVID EN CI A PU DAH UEL LO PRADO LA REI NA SANTIAGO CENTRO FINANCIERO Y NUNOA EST C ENTR AL COMERCIAL PENALOLEN P AGUIRRE C MACUL SAN JOAQUIN Sede de las casas matrices de CERRILLOS MAIPU SAN M IGUEL bancos y financieras y de la LO ESPEJO Bolsa de Comercio LA CISTERNA LA FLORI DA SAN RAMONLA GRANJ A - 61% colocaciones bancarias EL BOSQUE - 56% depósitos y captaciones bancarias PUENTE ALTO LA PIN TANA CENTRO DE EDUCACION SAN BERNARDO - 25% de la matrícula de educación superior a escala nacional CENTRO DE CULTURA SEDE DEL PODER POLITICO Actividades hacia la sostenibilidad Certificación Ambiental El municipio de Santiago ha trabajando desde el año 2005 en el “Sistema Nacional de Certificación Ambiental de Establecimientos Educacionales”, iniciativa impulsada por organismos del gobierno central en pos de fortalecer la educación ambiental. -

Actualización Plan De Desarrollo Comunal Lo Prado 2018
“ACTUALIZACIÓN PLAN DE DESARROLLO COMUNAL (PLADECO) COMUNA DE LO PRADO – REGIÓN METROPOLITANA DE SANTIAGO” ACTUALIZACIÓN PLAN DE INFORME FINAL DESARROLLO COMUNAL LO PRADO 2018 - 2022 INFORME FINAL Praxis Consultores Asociados Ltda. Marzo 2019 Versión 2.0 Presentación: Praxis Consultores Asociados Ltda. 318 “ACTUALIZACIÓN PLAN DE DESARROLLO COMUNAL (PLADECO) COMUNA DE LO PRADO – REGIÓN METROPOLITANA DE SANTIAGO” INFORME FINAL Presentación: El presente Plan de Desarrollo Comunal, es el resultado de un proceso de trabajo realizado durante los meses de Julio del año 2018 a Marzo del año 2019 y cuyo objetivo esencial, consistió en establecer de manera participativa, cuáles deben ser las estrategias, ejes e iniciativas de inversión a implementar por el municipio de Lo Prado y su Gobierno Local, de aquí al año 2022. Se destacan en el documento, los antecedentes estadísticos relativos a aspectos demográficos, económicos y sociales, una descripción de la gestión de diversas áreas del municipio, constatándose, la comprometida labor del conjunto de los funcionarios y funcionarias: También se destaca la relevante y significativa participación de alrededor 500 dirigentes y representantes de organizaciones sociales, de líderes locales y de vecinos y vecinas en general en los más de 30 talleres implementados en los Diálogos Vecinales en cada uno de los 4 Territorios de Planificación; talleres que permitieron establecer las principales necesidades, demandas o problemáticas más sentidas por la comunidad. Una vez establecido el conjunto de necesidades, se implementó una Consulta Ciudadana, a fin de que fuese la propia comunidad lopradina, la que, mediante un ejercicio de votación informada, libre y secreta, indicara cuáles debían ser las Iniciativas de Inversión que constituyese la Cartera de Proyectos del presente Plan de Desarrollo Comunal. -

Convencionales Constituyentes 9° Distrito Electoral Comunas: Conchalí, Renca, Huechuraba, Cerro Navia, Quinta Normal, Lo Prado, Recoleta E Independencia
CONVENCIONALES CONSTITUYENTES 9° DISTRITO ELECTORAL COMUNAS: CONCHALÍ, RENCA, HUECHURABA, CERRO NAVIA, QUINTA NORMAL, LO PRADO, RECOLETA E INDEPENDENCIA. REGIÓN METROPOLITANA DE SANTIAGO TERCER DOBLEZ CONSTITUYENTE D1 42x46,3 9° DISTRITO ELECTORAL PRIMER DOBLEZ SEGUNDO DOBLEZ SERVICIO ELECTORAL S L E A R R V -CO I O LES NV CI T PA EN C CI C O E I IO E L N L SÉPTIMO E N E SÉPTIMO U O A C I M L T IC - O E R V S R S A E E C L S L O A N N L S A O T I R S DOBLEZ I DOBLEZ T E O G R T 2021 U E V C R Y SERIE SVNN E I C E S L N I E E O R T O E E O I S D L C - A I E G N O R E B C V T R N° N°0000000 O E S R L A R O T C E L E O I C I V R E CONVENCIONALES CONSTITUYENTES 2021 S 0000000 N. LA LISTA DEL PUEBLO DISTRITO 9 XA. PARTIDO ECOLOGISTA VERDE XP. VAMOS POR CHILE 1 ALEJANDRA PIA PEREZ ESPINA, Independiente 8 NICOLE JORQUERA BRIONES 14 SOL LETELIER GONZALEZ, Unión Demócrata Independiente 2 PATRICIO ALEJANDRO CACERES ESCUDERO, Independiente 9 RAUL ALFREDO CORTES CASTILLO 15 ARTURO ZUÑIGA JORY, Unión Demócrata Independiente 3 GLORIA SOLEDAD PINTO BECERRA, Independiente 10 PATRICIA NUÑEZ AVILA 16 YIUYIUNIZ NAVAS DE CASO, Independiente Unión Demócrata Independiente 4 MATIAS NICOLAS ROA ROA, Independiente 11 VICENTE ORELLANA HIDALGO 17 FELIPE OBAL DURAN, Renovación Nacional 5 NATALIA ESTHER HENRIQUEZ CARREÑO, Independiente 12 PAULA STEFANI MORA DA SILVA 18 RUTH OLIVERA DE LA FUENTE, Independiente Renovación Nacional 6 MISAEL EDUARDO ARMIJO FUENTES, Independiente 13 ADRIAN ALBERTO VALENCIA VIDAL 19 DUILIO RENZO DE LAPEYRA PALMA, Independiente Evolución Política 7 MARLENE ELIZABETH SOTO GODOY, Independiente 20 XIMENA FRANCISCA AYALA FARIAS, Independiente Evolución Política SEXTO SEXTO DOBLEZ DOBLEZ YB. -

Regiones, Zonas, Juzgados, Comunas Y Causas a Licitar
A. RESUMEN NACIONAL . Zonas de licitación: El país se encuentra dividido en 71 zonas. Universo de causas a licitar: A nivel nacional, se proyecta un total aproximado de 538.400 causas susceptibles de ser mediadas durante el período de tres años, dicha cifra se denominará Total de Causas Proyectado a 3 años. Detalle Nacional: Total de Causas Proyectado Total Nacional a 3 Años 538.400 B. XV REGIÓN DE ARICA Y PARINACOTA . Zonas de licitación: Esta región contempla 1 zona de licitación. Universo de causas a licitar: En la Región de Arica y Parinacota, se proyecta un total aproximado de 8.800 causas susceptibles de ser mediadas durante el período de tres años, que contemplan los contratos respectivos, dicha cifra se denominará Total de Causas Proyectado a 3 años. Porcentaje a pagar por causa en trámite: En relación con el precio a pagar por causa en trámite en este caso corresponde a un 30% del precio que se paga por causa terminada con acuerdo total. Detalle Regional. XV Región de Arica y Parinacota Total de Causas Total de Causas Jurisdicción Zona Juzgado Proyectado por Proyectado a 3 Tribunal Juzgado a 3 A ños Años Juzgado de Arica / Camarones / A Familia de Putre / General 8.800 8.800 Arica Lagos Total Regional 8.800 C. I REGIÓN DE TARAPACÁ . Zonas de licitación: Esta región contempla 1 zona de licitación. Universo de causas a licitar: En la Región de Tarapacá, se proyecta un total aproximado de 13.600 causas susceptibles de ser mediadas durante el período de tres años, que contemplan los contratos respectivos, dicha cifra se denominará Total de Causas Proyectado a 3 años. -

Road Pricing in Urban Hazmat Transportation: a Practical Assessment Department of Transport Engineering Pontificia Universidad Católica De Chile
Road Pricing in Urban HazMat Transportation: A Practical Assessment Department of Transport Engineering Pontificia Universidad Católica de Chile Rodrigo A. Garrido Andrés Bronfman Why do we ned to move Hazmat? Hazmat include: explosives, flammable, oxidant, poisonous, infectious, radioactive, or corrosive substances among others Industrial production processes use hazmat as manufacturing components and often generate hazmat by-products. Hazmat must be safely transported from their origin to special facilities to be used in a production process, modified to decrease their degree of danger, or properly disposed. Why is it such a big deal? Enormous social relevance! Moving hazmat through populated areas poses a threat to the human health and the environment. In spite of the continuous efforts to mitigate harmful effects accidents do occur causing deaths, injuries and losses. These effects can be measured in monetary value But... these effects are probabilistic in nature The probability of an accident Identify and evaluate scenarios for the occurrence of an incident involving hazmat Scenarios can be described as a sequence of events. The events can be represented in a tree structure, showing a sequential progression of branched options: event tree r pPPPPPPa=⋅ a ya ⋅ fva ⋅ ha ⋅ har ⋅ char Outcome of the event tree: Prob of a catastrophic accident in arc a is a freight vehicle carries hazmat of type r r pPPPPPPa=⋅ ayafvahaharchar ⋅ ⋅ ⋅ ⋅ fall, collision, crash or overturn is carrying any hazmat Vehicle carrying hazmat r has catastrophic -

Ordenanza Del Plan Regulador Metropolitano De Santiago, Lo Que No Aparece Suficientemente Graficado En Los Planos RM-ZIER-LG-99-1 Y 2
Secretaría Ministerial Metropolitana de Vivienda y Urbanismo – Unidad Desarrollo Urbano – Área Planificación – Ordenanza PRMS _____________________________________________________________________________________________________________________ ORDENANZA PLAN REGULADOR METROPOLITANO DE SANTIAGO TEXTO ACTUALIZADO Y COMPAGINADO TITULO 1º: DISPOSICIONES GENERALES Artículo 1.1. El Plan Regulador Metropolitano de Santiago, en adelante el Plan Metropolitano, está conformado por la presente Ordenanza, los Planos RM-PRM-92-1.A, RM-PRM-92-1.A.1., RM-PRM-92-1.A.2., RM-PRM-93-1.A.4., RM-PRMS-03-1.A../1.A.5/70, RM-PRM-93-1.A.6., RM-PRM-92-1.B, Plano RM-PRM-93-T, Plano RM-PRM-95- CH.1.A., Plano RM-PRM-99-CH.2.B(*)., Plano RM-PRM-95.CH.1.C., Plano RM-PRMS-15/98, Plano RM-PRM- 01-CH.1.B/22(*)1, RM-PRM-02-pTM/cBP-1.A. y RM-PRM-02-pTM/cBP-1.C. y la Memoria Explicativa, que le complementan y que para los efectos de su aplicación constituyen un sólo cuerpo legal. (1), (b), (a), (b)*(a), (1)4 Los planos señalados en el inciso anterior se reemplazarán y/o modificarán por los planos que se indican en el siguiente cuadro: Plano Original Plano que reemplaza y/o modifica RM-PRM-92/1A RM-PRM-99-1.A/14 (modifica) (1)* RM-PRM-ZIER-01-1A/A9B (1)*** RM-PRM-99-1A/29 (modifica) (1)**** RM-PRM-02-1A/9LR (modifica) (1)º RM-PRM-02-1A/66 (modifica) (1)2 RM-PRM-05-1A/56 (modifica) (1)c RM-PRM-05-1A/80 (modifica) (1)3 RM-PRM-92/1A1 RM-PRM-99-1.A.1/14 (modifica) (1)* RM-PRM-01-1A1/45 (modifica) (1)** RM-PRM-99-1A/29 (modifica) (1)**** RM-PRM-01-1A1/50 (modifica) (1)***** RM-PRM-04-1A1/82 (modifica) (1)1 RM-PRM-05-1A1/80 (modifica) (2)3 RM-PRM-05-1A1/88 (modifica) RM-PRM-92/1A2 --- RM-PRM-93/1A4 --- RM-PRM-93/1A5 RM-PRMS-03-1.A./1.A.5/70 (reemplaza) (b) RM-PRM-93/1A6** --- RM-PRM-92/1B --- RM-PRM-93T* RM-PRM-99-1A/29 (modifica) (1)**** RM-PRM-02-T/57 (modifica) (1)b Plano RM-PRM95-CH.1.A. -

Plan Regional De Ordenamiento Territorial (PROT) Región Metropolitana De Santiago (RMS)
DIVISIÓN DE PLANIFICACIÓN Y DESARROLLO DEPARTAMENTO DE PLANIFICACIÓN REGIONAL Plan Regional de Ordenamiento Territorial (PROT) Región Metropolitana de Santiago (RMS) Informe de la Etapa 3 Propuesta del PROT RMS: “Unidades de gestión territorial, medidas y requerimientos a los usos del territorio, según división política-administrativa. Región Metropolitana de Santiago” Autores: Gerardo Ubilla Bravo Geógrafo y Licenciado en geografía Departamento de Planificación Regional División de Planificación y Desarrollo Elizabeth Galdámez Roco Licenciada en Ciencias de los Recursos Naturales Renovables Universidad de Chile Santiago de Chile Enero de 2015 ______________________________________________________________________________________________ Bandera 46 • Santiago de Chile • www.gobiernosantiago.cl DIVISIÓN DE PLANIFICACIÓN Y DESARROLLO DEPARTAMENTO DE PLANIFICACIÓN REGIONAL CONTENIDOS I. INTRODUCCIÓN ....................................................................................................... 4 II. MARCO METODOLÓGICO......................................................................................... 5 1. Marco general de análisis......................................................................................................................5 2. Pasos metodológicos.............................................................................................................................5 III. DESCRIPCIÓN DE LAS UNIDADES DE GESTIÓN SEGÚN DIVISIÓN POLÍTICA- ADMINISTRATIVA DE LA REGIÓN ................................................................................ -

Código Azul, Para Proteger a Gente Que Vive En Situación De Calle ¡Ayúdalos!
CÓDIGO AZUL, PARA PROTEGER A GENTE QUE VIVE EN SITUACIÓN DE CALLE ¡AYÚDALOS! ES RESPONSABILIDAD DE TODOS ¡Acércate, Alerta y Actúa! u Si encuentras a una Persona en Situación de Calle, acércate, pregúntale cómo se siente, qué necesita y colabora enviando una alerta o trasladando a un refugio a quien lo requiera. u Puedes dar la alerta en el link: https://codigoazul.ministeriodesarrollosocial.gob.cl/formulario-alerta u Puedes pedir ayuda en: Puedes dar la alerta en el link: https://codigoazul.ministeriodesarrollosocial.gob.cl/formulario-alerta PASOS PARA DAR ALERTA Centros para la Superación Listado de albergues de la Región Metropolitana Región Tipo Comuna Nombre Dirección Institución Horario Cupos José Miguel Carrera 433, Buin, Región Municipalidad Metropolitana Albergue Buin Albergue 24 hrs. 20 Metropolitana, Chile de Buin Av. Diagonal Cardenal José María Fundación Metropolitana Albergue Conchalí Albergue Caro 1851, Conchalí, Región 24 hrs 20 Hogar de Cristo Metropolitana, Chile San Fernando 1262, Conchalí, Región Municipalidad Metropolitana Albergue Conchalí Albergue 24 hrs 20 Metropolitana, Chile de Conchalí Albergue C-19 Albergue Plan Av Libertador Bernardo O'Higgins 3138, Parroquia Fundación Metropolitana Protege Calle Estación Central Santiago, Estación Central, Región 24 hrs 20 Sagrado Mission Golden COVID-19 Metropolitana, Chile Corazón Las Perdices 6987, La Florida, Región Fundación Metropolitana Albergue La Florida Albergue 24 hrs. 20 Metropolitana, Chile Educere Trinidad 1767, La Florida, Iglesia Volver a Metropolitana Albergue La Florida Albergue Región Metropolitana, 24 hrs 20 Vivir Chile Padre Esteban Gumucio Fundación Vives 498, La Granja, Metropolitana Albergue La Granja Albergue Damián 24 hrs 20 Región Metropolitana, Molokai Chile Los Plátanos 658, La Fundación Metropolitana Albergue La Pintana Albergue Pintana, Región 24 hrs. -

Region Metropolitana
MINISTERIO DE VIVIENDA Y URBANISMO SECRETARÍA REGIONAL MINISTERIAL DE VIVIENDA Y URBANISMO Región: REGION METROPOLITANA PROGRAMA DE PAVIMENTACIÓN PARTICIPATIVA LISTA DEFINITIVA DE PROYECTOS SELECCIONADOS PROCESO DE SELECCIÓN, CIERRE 30-12-2020 PROYECTOS SELECCIONADOS COMUNA PRIORIDAD PUNTAJE TOTAL N° FICHA NOMBRE UNIDAD VECINAL TIPO VÍA NOMBRE CALLE O PASAJE TRAMO LONGITUD BUIN 1 183,89 13474 JJVV EL QUIJOTE Aceras GUARDIA MARINA RIQUELME 3 ERRAZURIZ-PASAJE MONONA 98 BUIN 2 170,92 13469 LOS COPAHUES Aceras VEREDA LORD COCHRANNE KENNEDY-ALMIRANTE WILLIAMS 167 BUIN 3 167,35 13295 13 Manuel Rodríguez-Las Rejas Pasaje PASAJE PORTUGAL LUXEMBURGO-FIN 30 BUIN 4 161,06 13611 JJVV VILLA VIRGINIA Aceras SAN IGNACIO SAN ANOTNIO-KENNEDY 160 BUIN 5 156,19 13450 LOS COPAHUES Aceras VEREDA ALMIRANTE WILLIAMS GUARDIA MARINA RIQUELME-FIN SUR 310 BUIN 6 151,29 13466 JUNTA DE VECINOS VILLA EL DIAMANTE Pasaje TURQUESA SUR M. RODRIGUEZ-FIN SUR 38 BUIN 7 149,11 13432 14 Manuel Plaza Pasaje PASAJE 1 PONIENTE FREIRE-FIN PONIENTE 173 BUIN 8 147,47 13440 JJVV VILLA MAGISTERIO Pasaje PASAJE LOS CRISANTEMOS MONTT-FIN 35 BUIN 9 146,21 13435 JJVV VILLA GABRIELA Aceras VEREDA SAN SEBASTIAN ERRAZURIZ-KENNEDY 286 BUIN 10 143,73 13352 JJVV VILLA EL PROGRESO MAIPO Pasaje PASAJE EL TORDILLO EL PERCHERON-LA COSECHA 81 BUIN 11 141,12 13617 LOS COPAHUES Aceras VEREDA GUARDIA MARINA RIQUELME 4 KENNEDY-FIN PONIENTE 205 BUIN 12 137,63 13470 JJVV EL QUIJOTE Pasaje PASAJE SAN SEBASTIAN ANIBAL PINTO-FIN ORIENTE 93 BUIN 13 137,1 13618 JJVV CARLOS FIGUEROA UNIDO Pasaje PASAJE LOS