DOCSLIB.ORG

The Consequences of Broadcasting, Brooding, and Asexual Reproduction

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
The Consequences of Broadcasting, Brooding, and Asexual Reproduction OCEANOLOGICA ACTA- VOL. 19- W3-4 ~ -----~- Life-cycle The consequences of broadcasting, Demography Asteroidea brooding, and asexual reproduction Transition matrix Cycle de vie Démographie in echinoderm metapopulations Asteroidea Matrices de transition Thomas A. EBERT Department of Biology, San Diego State University, San Diego, CA 92182-4614 USA. Received 17/01/95, in revised form 22/01/96, accepted 23/01/96. ABSTRACT Different modes of reproduction were examined in the context of entire life cycles for seven starfish species so that adult survival could be compared with reproductive output and first year survival. Data were assembled from the litera­ ture and included two asexual species, Linckia multifora and Nepanthia belcheri; two brooders, Asterina phylactica and Leptasterias hexactis; one species with benthic eggs that does not brood, Asterina gibbosa; one species with lecithotro­ phic development in the plankton, Patiriella pseudoexigua; and one planktotro­ phic species, Pisaster ochraceus. A negative correlation was found between first­ year survival and adult survival rates which also correlated with mode of reproduction: highest adult survival and lowest first-year survival was found for P. ochraceus, the planktotrophic species, and lowest adult survival was coupled with highest first-year survival in asexual species. A matrix model was developed to explore the metapopulation consequences of different modes of reproduction. Asexual species are similar to species with planktonic larvae that also have long-lived adults in that both are weil insulated from the vagaries of planktonic life, one by avoiding the plankton ali together and the other by having very low transition probabilities for the first year of life but high transition probabilities for retention of adults in the population. Species with short-lived adults and planktonic development of larvae are more closely tied to changes in first-year survival rates with respect to over-all dynamics of metapopulations. RÉSUMÉ Les conséquences de divers modes de reproduction, production de larves pélagiques, incubation et reproduction asexuée chez les métapopulations d'échinodermes. Différents modes de reproduction sont examinés à travers les cycles vitaux de sept espèces d'étoiles de mer; le taux de survie des adultes est comparé à la pro­ duction gonadique et au taux de survie durant la première année. Les données, extraites de la littérature, se rapportent à 1) deux espèces asexuées, Linckia multi­ fora et Nepanthia belcheri, 2) deux espèces incubantes, Asterina phylactica et Leptasterias hexactis, 3) une espèce à développement benthique qui ne protège pas ses œufs, Asterina gibbosa, 4) une espèce à développement planctonique lécithotrophique, Patiriella pseudoexigua, et 5) une espèce planctotrophique, Pisaster ochraceus. Une corrélation négative est observée entre le taux de survie durant la première année et le taux de survie des adultes, lui-même corrélé au mode de reproduc­ tion. Le plus fort taux de survie des adultes et le plus faible taux de survie durant la première année sont observés chez P. ochraceus, l'espèce planctotrophique, 217 T.A. EBERT tandis que le plus faible taux de survie des adultes est associé au plus fort taux de survie durant la première année chez les espèces asexuées. Un modèle matriciel a été développé pour analyser les conséquences des diffé­ rents modes de reproduction chez les métapopulations. Les espèces asexuées sont similaires aux espèces à larves planctoniques et longue durée de vie, dans la mesure où toutes deux échappent aux caprices de la vie pélagique, les unes ne dépendant pas du plancton en général, les autres ayant peu de chances de survie au-delà de la première année mais une forte probabilité de maintien des adultes dans la population. Les espèces à courte durée de vie et à développement larvaire planctonique ont un taux de survie nettement plus variable durant leur première année, en rapport avec la dynamique des métapopulations. OceanologicaActa, 1996,19,3-4,217-226. INTRODUCTION with transition probabilities, and there are none that supply such information so spatial and temporal variability can be evaluated. Y et it is clear that such information is needed Life cycles of organisms represent a long history of selec­ not only to understand the evolution of life histories but tive tinkering and, in general, the !ife cycle that is observed also for applied purposes such as management of natural is expected to show adjustments in ali parts of the cycle in resources and the design of marine reserve systems. response to changes in one part. Schedules of survival and reproduction are at the core of ali theoretical discussions of This paper examines data on echinoderms, and in particu­ life cycles dating back to Fisher (1930), Birch (1948), and lar starfishes, to evaluate the effects of different reproducti­ Cole (1954) and implicit or explicit in ali life-history dis­ ve modes on transitions in the life cycle, specifically first­ cussions is that trade-offs exist such that if resources are year and adult survival rates. Also, after making estimates used for one activity they can not be used for something of these transitions for a selection of echinoderm species, 1 else. Analysis of tradeoffs bas focused on relationships will present a mode! for combining populations into meta­ among numbers and sizes of offspring, adult size and populations that provides sorne insights into the importan­ growth, and survival (e.g, Stearns, 1992). ce of dispersal with respect to fitness and probable stability characteristics of metapopulations of species with different Population growth rate or fitness is determined by mean modes of reproduction. values for schedules of survival and fecundity as weil as variability of these traits (e.g. Tuljapurkar, 1982 a, b; Orzack, 1985; Caswell, 1989) and so changes in morpholo­ gy, physiology, or behavior that change means and METHODS variances of life-cycle transitions will change fitness. Changes in mean values for offspring number are correla­ ted with mode of reproduction in marine invertebrates, as Life-cycle information in the form of age- or size-specific weil as other groups of organisms, and these changes in rates of survival and reproduction was obtained from a mode of reproduction are perceived as changes that should number of published studies. To reanalyze data, 1 bad to modify early survivorship (e.g. Menge, 1975). make a number of assumptions. The two most important assumptions are: 1) populations have seasonally stable There is general agreement concerning the ranking of structure; that is, at the same time each year they have the reproductive modes that should improve the chances of same proportions in ages or sizes; and, 2) populations are first year survival: the form of reproduction with the lowest seasonally stationary, which means that from year to year first-year survival is planktotrophy, followed by planktonic the population growth rate, Â, is equal to 1.0. lecithotrophy, attached benthic lecithotrophic eggs with no planktonic stage, brooding, and, finally, asexual reproduc­ Two different, though related, forms of the life cycle were tion, such as autotomy of body parts that regenerate, and used for analysis (Figs. 1, 2). In the first (Fig. 1), an age­ fission of a body into two or more pieces of approximately structured matrix was created with a terminal age, ro, and equal size. Asexual reproduction should have the highest with the possibility of age-specifie changes in reproduction first year survival rate. and survival for adults. This is the standard Leslie matrix. Data that were used included ali information but one tran­ Changes that increase the mean and reduce variation in sition; namely, first year survival Po. The characteristic survival from spawning or asexual reproduction to an age equation for Figure 1 was obtained by following the outli­ of one year should improve fitness and as a consequence ne provided by Casweli (1985, 1989). A Z-transformation free resources that bad been used for maintenance to was performed, which is just multiplying ali transitions by increase fitness in other ways, such as more offspring. This Â-l. Ali possible loops through node 1 were determined scenario bas been presented by Stearns (1976) and conti­ and then ali transitions in a loop were multiplied together. nues to be an attractive explanation (e.g. Grant, 1990). Products from ali individual loops were then added toge­ Few studies on life-history traits of echinoderm species ther and set equal to 1.0. A bit of additional algebra was ali with different modes of reproduction have been conducted that was needed to form the characteristic equation of the in sufficient detail that complete !ife-cycles can be drawn graph: 218 ECHINODERM METAPOPULATIONS St =Soo(1- e-Z) :~:e-Zi (1- b.e-K(t+i) )-n (5) i=O With the Richards function for modeling growth and constant adult survival the parameters in Eq. 5 are: 1 2 Â. ro- b1 PoÂ.ro- - b2PoÂ. ro- ... bwPo = 0 Soo = asymptotic size 1 K = the growth-rate constant with units of ti me-1 n =a shape parameter; e.g. n =-1 for the Brody-Bertalanf­ fy equation and + 1 for logistic growth Figure 1 s-IIn -S-1/n Life-cycle with age-structure that is the equivalent of the Leslie b= oo R (6) s-lln matrix; Po = first year survival; Px = age-specifie survival for age 00 classes from 1 to oo; mx = age-specifie fecundity; formula for estima­ ting Pois for population growth rate Â. set equal to 1. t = time since recruitment of animais that are size SR; t generally is set equal to O. SR = size of new recruits, generally set as equal to the mode of the smallest component of a size-frequency distri­ (1) bution or series of size-frequency distributions. where b1 is m~o bz is P1m2, b3 is P1P2m3, etc. After setting Z =the instantaneous rate of mortality when Nx = Noe-Zx Â.
Load more

Recommended publications
  • ENL 12.Pdf (2.8
    , . THE ECHINODERMS NEWSLETTER •I No. 12. Ju1Yt 1982 JIIH B 3 35 PM'63 Distributed by the Department of Invertebrate Zoology, 1 .., ,~ National Museum of Natural History MAl L S E i~VI C L .:;, Smithsonian Institution CEl-iTER Washington, D. C.t U. S. A. " Editor: .fohn M. La'tlTrence ~epartment of Biology Vniversity of South Florida tampat Florida 33620 U. S. A. / / Assistants: Chang-Po Chen, Walter Diehl, Adam Marsh, James McClintockt Stephen Watts ) The Echi~oderms Newsletter was founded in 1968 by David L. Pawson and Maureen E. Downey o~ th~ Smithsonian Institution. They were responsible for the preVious eleven i~sues. Workers with echinoderms, and indeed those who work with fl1 invertebfates, owe them a tremendous debt for the contribution which the #ewsletter has made/to the field. c' "., The neWs~etter generally contains information concerning meetings and conferences and publtcations of interest to echinoderm biologists, titles of theses a,d "-disserta~ions on echinoderms, and research interests and addresses of echlnoderm biologists. To insure inclU$~on~~ journal articles in the newsletter, a~thors are -.requeste4 to send titles or"reprints to the editor. }, ..,.. / SuggestiOns and request,s'from individuals can be addressed to the entire !chinoderm biology ~ommunity th~ough the newsletter. /'~. ," The news~etter ,;f:'s'~~otintendedto be a part of the scientific literature,' and should n~t be/c:ited, abstracted, or reprinted as a published document. •..., " ---- ..•..,->.--------------~--------------------." ./ .' -'. ~:-/.;, Internat+onal Echinoderms Conference--Tampa Bay (1981) /', '.--:. The inte{nati6~al echinoderms conferences began with the Smithsonian meet~ng In 1972. At that conference, participants voted to have subsequent internat!ona1 /lIleetingsevet'! three years, with the site to be changed.between the Ap1eri~as, Europe? fil-ndjtheEast.
    [Show full text]
  • The Sea Stars (Echinodermata: Asteroidea): Their Biology, Ecology, Evolution and Utilization OPEN ACCESS
    See discussions, stats, and author profiles for this publication at: https://www.researchgate.net/publication/328063815 The Sea Stars (Echinodermata: Asteroidea): Their Biology, Ecology, Evolution and Utilization OPEN ACCESS Article · January 2018 CITATIONS READS 0 6 5 authors, including: Ferdinard Olisa Megwalu World Fisheries University @Pukyong National University (wfu.pknu.ackr) 3 PUBLICATIONS 0 CITATIONS SEE PROFILE Some of the authors of this publication are also working on these related projects: Population Dynamics. View project All content following this page was uploaded by Ferdinard Olisa Megwalu on 04 October 2018. The user has requested enhancement of the downloaded file. Review Article Published: 17 Sep, 2018 SF Journal of Biotechnology and Biomedical Engineering The Sea Stars (Echinodermata: Asteroidea): Their Biology, Ecology, Evolution and Utilization Rahman MA1*, Molla MHR1, Megwalu FO1, Asare OE1, Tchoundi A1, Shaikh MM1 and Jahan B2 1World Fisheries University Pilot Programme, Pukyong National University (PKNU), Nam-gu, Busan, Korea 2Biotechnology and Genetic Engineering Discipline, Khulna University, Khulna, Bangladesh Abstract The Sea stars (Asteroidea: Echinodermata) are comprising of a large and diverse groups of sessile marine invertebrates having seven extant orders such as Brisingida, Forcipulatida, Notomyotida, Paxillosida, Spinulosida, Valvatida and Velatida and two extinct one such as Calliasterellidae and Trichasteropsida. Around 1,500 living species of starfish occur on the seabed in all the world's oceans, from the tropics to subzero polar waters. They are found from the intertidal zone down to abyssal depths, 6,000m below the surface. Starfish typically have a central disc and five arms, though some species have a larger number of arms. The aboral or upper surface may be smooth, granular or spiny, and is covered with overlapping plates.
    [Show full text]
  • A Systematic Revision of the Asterinid Genus Aquilonastra O'loughlin
    Memoirs of Museum Victoria 63(2): 257–287 (2006) ISSN 1447-2546 (Print) 1447-2554 (On-line) http://www.museum.vic.gov.au/memoirs/index.asp A systematic revision of the asterinid genus Aquilonastra OʼLoughlin, 2004 (Echinodermata: Asteroidea) P. M ARK OʼLOUGHLIN1 AND FRANCIS W.E. ROWE2 1Honorary Associate, Marine Biology Section, Museum Victoria, GPO Box 666, Melbourne, Vic. 3001, Australia ([email protected]) 2Research Associate, Australian Museum, Sydney, NSW, Australia ([email protected]). Private address: Beechcroft, Norwich Road, Scole, Diss, Norfolk, IP21 4DY, U.K. Abstract OʼLoughlin, P. Mark and Rowe, Francis W.E. A systematic revision of the asterinid genus Aquilonastra OʼLoughlin, 2004 (Echinodermata: Asteroidea). Memoirs of Museum Victoria 63(2): 257–287. The Indo-west Pacifi c Aquilonastra OʼLoughlin is reviewed. Eleven species are retained in Aquilonastra: A. anomala (H.L. Clark); A. batheri (Goto); A. burtonii (Gray); A. cepheus (Müller and Troschel); A. corallicola (Marsh); A. coronata (Martens); A. iranica (Mortensen); A. limboonkengi (Smith); A. minor (Hayashi); A. rosea (H.L. Clark); A. scobinata (Livingstone). Asterina lorioli Koehler is reassigned to Aquilonastra. Thirteen new species are described: A. byrneae; A. colemani; A. conandae; A. doranae; A. halseyae; A. marshae; A. moosleitneri; A. oharai; A. richmondi; A. rowleyi; A. samyni; A. watersi; A. yairi. The four subspecies of Asterina coronata Martens are junior synonyms: Asterina coronata cristata Fisher; Asterina coronata euerces Fisher; Asterina coronata fascicularis Fisher; Asterina coronata forma japonica Hayashi. The 13 fi ssiparous Red Sea specimens described by Perrier as Asteriscus wega are the syntypes. Asteriscus wega Perrier is a junior synonym of Asterina burtonii Gray.
    [Show full text]
  • Rocky Shore Guide
    Welcome to The Seashore Code Help protect Devon’s special coastline by Wembury following the Seashore Code every time you go rockpooling. Right way up! Enjoy looking under rocks but always replace them carefully, just how you found them. Devon Wildlife Trust’s One at a time Guide to common seaweeds Always put seawater in your Wembury in South Devon is a magnet for wildlife bucket first and no more than one – its rocky cliffs are home to nesting seabirds and and rocky shore species creature at a time. the rocky shore, slate reefs and massive wave-cut platforms provide one of the United Kingdom’s best No nets! spots for marine life. Wembury and the surrounding Be gentle catching animals in coastline form a Marine Conservation Area (MCA), a rockpools – use your hands, not Special Area of Conservation (SAC), a Site of Special nets. Scientific Interest (SSSI) and form part of the South Devon Area of Outstanding Natural Beauty (AONB). Put me back These go some way to shielding it from human Many animals have special homes pressures. so always return them to where they were found. Managed by Devon Wildlife Trust, Wembury Marine Centre is the ideal place to learn about the Watch your step! surrounding marine environment and its wildlife Take care not to damage seashore through regular rockpool and snorkel safaris, school creatures underfoot or by pulling visits and other marine-themed events. The Centre them off rocks. also explains the part you can play in protecting your local marine environment, following The Wildlife Be safe; be kind Trusts’ Living Seas strategy.
    [Show full text]
  • <I>Patiriella Vivipara</I> (Echinodermata: Asteroidea
    AUSTRALIAN MUSEUM SCIENTIFIC PUBLICATIONS Prestedge, G. K., 1998. The distribution and biology of Patiriella vivipara (Echinodermata: Asteroidea: Asterinidae) a sea star endemic to southeast Tasmania. Records of the Australian Museum 50(2): 161–170. [7 October 1998]. doi:10.3853/j.0067-1975.50.1998.1277 ISSN 0067-1975 Published by the Australian Museum, Sydney naturenature cultureculture discover discover AustralianAustralian Museum Museum science science is is freely freely accessible accessible online online at at www.australianmuseum.net.au/publications/www.australianmuseum.net.au/publications/ 66 CollegeCollege Street,Street, SydneySydney NSWNSW 2010,2010, AustraliaAustralia Records of the Australian Museum (1998) Vol. 50: 161-170. ISSN 0067-1975 The Distribution and Biology of Patiriella vivipara (Echinodermata: Asteroidea: Asterinidae) a Sea Star Endemic to Southeast Tasmania GEOFFREY K. PRESTEDGE 16 Geeves Crescent, Midway Point Tasmania 7171, Australia ABSTRACT. The asterinid sea star Patiriella vivipara is endemic to southeast Tasmania and has a highly restricted distribution, being only known from four locations. It has an unusual pattern of viviparous reproduction, giving birth to juveniles. In this study the birth rate, growth rate, size and age at commencement of reproduction of P vivipara was examined in aquaria for a period of six years. The population of P vivipara at Pittwater was also monitored through monthly examination of a permanent 1m2 quadrat in which the number of adults and juveniles were counted and recorded. These counts were made over an eight-year period. Patiriella vivipara gives birth to juveniles through the year with a period of enhanced reproduction from November to January. Records of water salinity and temperature were taken at Pittwater, as were air temperatures and exposure times during low tide.
    [Show full text]
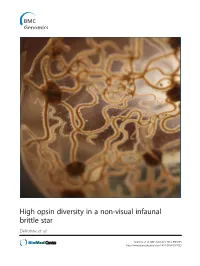
  • Amphiura Filiformis, We First Highlighted a Blue-Green Light Sensitivity Using a Behavioural Approach
    High opsin diversity in a non-visual infaunal brittle star Delroisse et al. Delroisse et al. BMC Genomics 2014, 15:1035 http://www.biomedcentral.com/1471-2164/15/1035 Delroisse et al. BMC Genomics 2014, 15:1035 http://www.biomedcentral.com/1471-2164/15/1035 RESEARCH ARTICLE Open Access High opsin diversity in a non-visual infaunal brittle star Jérôme Delroisse1*, Esther Ullrich-Lüter2, Olga Ortega-Martinez3, Sam Dupont3, Maria-Ina Arnone4, Jérôme Mallefet5 and Patrick Flammang1 Abstract Background: In metazoans, opsins are photosensitive proteins involved in both vision and non-visual photoreception. Echinoderms have no well-defined eyes but several opsin genes were found in the purple sea urchin (Strongylocentrotus purpuratus) genome. Molecular data are lacking for other echinoderm classes although many species are known to be light sensitive. Results: In this study focused on the European brittle star Amphiura filiformis, we first highlighted a blue-green light sensitivity using a behavioural approach. We then identified 13 new putative opsin genes against eight bona fide opsin genes in the genome of S. purpuratus. Six opsins were included in the rhabdomeric opsin group (r-opsins). In addition, one putative ciliary opsin (c-opsin), showing high similarity with the c-opsin of S. purpuratus (Sp-opsin 1), one Go opsin similar to Sp-opsins 3.1 and 3.2, two basal-branch opsins similar to Sp-opsins 2 and 5, and two neuropsins similar to Sp-opsin 8, were identified. Finally, two sequences from one putative RGR opsin similar to Sp-opsin 7 were also detected. Adult arm transcriptome analysis pinpointed opsin mRNAs corresponding to one r-opsin, one neuropsin and the homologue of Sp-opsin 2.
    [Show full text]
  • Marine Genomics Meets Ecology: Diversity and Divergence in South
    Marine genomics meets ecology: Diversity and divergence in South African sea stars of the genus Parvulastra Katherine Dunbar Thesis submitted for the degree of Doctor of Philosophy Biodiversity and Ecological Processes Research Group School of Biosciences Cardiff University December 2006 UMI Number: U584961 All rights reserved INFORMATION TO ALL USERS The quality of this reproduction is dependent upon the quality of the copy submitted. In the unlikely event that the author did not send a complete manuscript and there are missing pages, these will be noted. Also, if material had to be removed, a note will indicate the deletion. Dissertation Publishing UMI U584961 Published by ProQuest LLC 2013. Copyright in the Dissertation held by the Author. Microform Edition © ProQuest LLC. All rights reserved. This work is protected against unauthorized copying under Title 17, United States Code. ProQuest LLC 789 East Eisenhower Parkway P.O. Box 1346 Ann Arbor, Ml 48106-1346 DECLARATION This work has not previously been substance for any degree and is not being concurrently submitted in c y degree. Signed ................................(candidate) Date.... 3 l . ™ MW. ... ..... STATEMENT 1 This thesis is the result of my own M ent work/investigation, except where otherwise stated. Other source* edged by footnotes giving explicit references. Signed (candidate) S.**: Q tife : ...... STATEMENT 2 I hereby give consent for my thesis, if accepted, to be available for photocopying and for inter-library loan, and for the tJfJSJa^^prrmqary to be made available to outside organisations Signed ................................................................... (candidate) Date............................. Abstract The coast of South Africa is situated between the warm Indian and the cold Atlantic Oceans, resulting in an extreme intertidal temperature gradient and potentially strong opposing selection pressures between the east and west coasts.
    [Show full text]
  • A Cushion Star (Asterina Phylactica)
    MarLIN Marine Information Network Information on the species and habitats around the coasts and sea of the British Isles A cushion star (Asterina phylactica) MarLIN – Marine Life Information Network Marine Evidence–based Sensitivity Assessment (MarESA) Review Morvan Barnes 2008-03-27 A report from: The Marine Life Information Network, Marine Biological Association of the United Kingdom. Please note. This MarESA report is a dated version of the online review. Please refer to the website for the most up-to-date version [https://www.marlin.ac.uk/species/detail/131]. All terms and the MarESA methodology are outlined on the website (https://www.marlin.ac.uk) This review can be cited as: Barnes, M.K.S. 2008. Asterina phylactica A cushion star. In Tyler-Walters H. and Hiscock K. (eds) Marine Life Information Network: Biology and Sensitivity Key Information Reviews, [on-line]. Plymouth: Marine Biological Association of the United Kingdom. DOI https://dx.doi.org/10.17031/marlinsp.131.1 The information (TEXT ONLY) provided by the Marine Life Information Network (MarLIN) is licensed under a Creative Commons Attribution-Non-Commercial-Share Alike 2.0 UK: England & Wales License. Note that images and other media featured on this page are each governed by their own terms and conditions and they may or may not be available for reuse. Permissions beyond the scope of this license are available here. Based on a work at www.marlin.ac.uk (page left blank) Date: 2008-03-27 A cushion star (Asterina phylactica) - Marine Life Information Network See online review for distribution map Close-up of the aboral (top) side of a cushion star found in an intertidal rockpool.
    [Show full text]
  • SIGOVINI M., TAGLIAPIETRA D., 2008 – Segnalazione Di Un Esemplare
    Boll. Mus. civ. St. nat. Venezia, 59 (2008) 2009 69 Marco Sigovini, Davide Tagliapietra SEGNALAZIONE DI UN ESEMPLARE ESARAGGIATO DI ASTERINA GIBBOSA (PENNANT, 1777) IN LAGUNA DI VENEZIA (ECHINODERMATA: ASTEROIDEA) Riassunto. Si descrive il ritrovamento in Laguna di Venezia di un esemplare di Asterina gibbosa (Pennant, 1777) caratterizzato da sei braccia egualmente formate e funzionali. Si riportano le precedenti segnalazioni di tale carattere in A. gibbosa, con una sintetica rassegna sulle anomalie riguardanti il numero di braccia nelle specie pentaraggiate della famiglia Asterinidae. Summary. Note on a six-rayed specimen of Asterina gibbosa (Pennant, 1777) found in the Lagoon of Venice (Echin- odermata: Asteroidea). The finding of a six-rayed specimen of Asterina gibbosa (Pennant, 1777) in the Lagoon of Venice is described. All the rays were similar and functional. Previous reports of this character in A. gibbosa are quoted, with a brief review concerning the occurrence of anomalous number of rays in five-rayed Asterinidae species. Keywords: Asterinidae, pentamerism, symmetry. INTRODUZIONE Gli Echinodermi sono organismi solitamente stenoeci, e solo un numero ridotto di specie si è potuto adattare alle caratteristiche degli ambienti di transizione (VATOVA, 1950; BINYON, 1966). In Laguna di Venezia VATOVA (1950) segnalò la presenza di 15 specie, otto delle quali furono però ritrovate unicamente presso le bocche di porto. Delle rimanenti, solo cinque risul- tarono regolarmente diffuse. Tra queste ultime la classe Asteroidea era presente unicamente con Asterina gibbosa (Pennant, 1777). La sua presenza in Laguna di Venezia quale unico rappre- sentante della classe è stata confermata in più recenti studi (ad es. BALDUCCI et al., 2001; SFRISO et al., 2001) e monitoraggi (dati non pubblicati).
    [Show full text]
  • Community, Trophic Structure and Functioning in Two Contrasting Laminaria Hyperborea Forests
    1 Estuarine, Coastal and Shelf Science Achimer January 2015, Volume 152, Pages 11-22 http://dx.doi.org/10.1016/j.ecss.2014.11.005 http://archimer.ifremer.fr http://archimer.ifremer.fr/doc/00226/33747/ © 2014 Elsevier Ltd. All rights reserved. Community, Trophic Structure and Functioning in two contrasting Laminaria hyperborea forests Leclerc Jean-Charles 1, 2, * , Riera Pascal 1, 2, Laurans Martial 3, Leroux Cedric 1, 4, Lévêque Laurent 1, 4, Davoult Dominique 1, 2 1 Sorbonne Universités, UPMC Univ Paris 6, Station Biologique de Roscoff, Place Georges Teissier, 29680 Roscoff, France 2 CNRS, UMR 7144 AD2M, Station Biologique de Roscoff, Place Georges Teissier, 29680 Roscoff, France 3 IFREMER, Laboratoire de Biologie Halieutique, Centre Bretagne, BP 70,29280 Plouzané, France 4 CNRS, FR 2424, Station Biologique de Roscoff, Place Georges Teissier,29680 Roscoff, France * Corresponding author : Jean-Charles Leclerc, email address : [email protected] Abstract : Worldwide kelp forests have been the focus of several studies concerning ecosystems dysfunction in the past decades. Multifactorial kelp threats have been described and include deforestation due to human impact, cascading effects and climate change. Here, we compared community and trophic structure in two contrasting kelp forests off the coasts of Brittany. One has been harvested five years before sampling and shelters abundant omnivorous predators, almost absent from the other, which has been treated as preserved from kelp harvest. δ15N analyses conducted on the overall communities were linked to the tropho-functional structure of different strata featuring these forests (stipe and holdfast of canopy kelp and rock). Our results yielded site-to-site differences of community and tropho-functional structures across kelp strata, particularly contrasting in terms of biomass on the understorey.
    [Show full text]
  • Zootaxa 359: 1–14 (2003) ISSN 1175-5326 (Print Edition) ZOOTAXA 359 Copyright © 2003 Magnolia Press ISSN 1175-5334 (Online Edition)
    Zootaxa 359: 1–14 (2003) ISSN 1175-5326 (print edition) www.mapress.com/zootaxa/ ZOOTAXA 359 Copyright © 2003 Magnolia Press ISSN 1175-5334 (online edition) A new viviparous species of asterinid (Echinodermata, Asteroidea, Asterinidae) and a new genus to accommodate the species of pan- tropical exiguoid sea stars ALAN J. DARTNALL1, MARIA BYRNE2, JOHN COLLINS3 & MICHAEL W HART4 1 17 Kepler St, Wulguru, Queensland 4811, Australia email: [email protected] 2 Department of Anatomy & Histology, F-13, University of Sydney, Sydney, New South Wales 2006, Australia email: [email protected] 3 Department of Marine Biology, James Cook University, Townsville, Queensland 4811, Australia email:[email protected] 4 Department of Biology, Dalhousie University, Halifax, Nova Scotia, Canada email:[email protected] Abstract This paper describes a new species of viviparous, intragonadal brooder of asterinid sea star and clarifies the identities of Patiriella pseudoexigua Dartnall 1971, the species Patiriella pseudoex- igua sensu Chen and Chen (1992) and Patiriella pseudoexigua pacifica (Hayashi, 1977). The latter is raised to specific rank. Analysis of mitochondrial DNA supports the concept of a pan-tropical assemblage of species for which a new genus, Cryptasterina, is created. All species in Cryptaster- ina are morphologically similar and comprise species with planktonic, lecithotrophic, non-feeding larvae, and viviparous outlier species with limited distributions. The full diversity of this species diaspora remains to be resolved. Key words: Echinodermata; Asteroidea; Asterinidae; Cryptasterina new genus; new species; new combination; cryptic species; developmental biology; viviparity; tropical Introduction The sea star family Asterinidae has two species-rich genera, Asterina and Patiriella (Rowe and Gates 1996).
    [Show full text]
  • The Development of Ophiothrix Fragilis. 557
    THE DEVELOPMENT OF OPHIOTHRIX FRAGILIS. 557 The Development of Ophiothrix fragilis. By E. W. ftlacBridc, M.A., D.Sc, F.R.S., Professor of Zoology in McGill University, Montreal. With Plates 31—36, and 4 Text-figures. CONTENTS. PAGE Introduction ..... 557 Historical Sketch . .558 Material and Methods .... 567 Normal and Abnormal Development . 570 Tlie Development of the Full-grown Larva . 575 Metamorphosis of the Larva into the Brittle-star . 5S0 Comparison with Development in other Classes of Echino- dermata . 590 Summary and Conclusion .... 596 INTRODUCTION. THE present work, which has occupied my attention for the last four years, was begun with the object of extending to other classes of Echinoderms the researches which I had already made on the development of Asteroidea (18) and Echinoidea (19). It has proved to be a task of extraordinary difficulty owing to the minute and refractory character of the larvas oE Ophiuroidea. Nevertheless, the results obtained will, I think, bear fair comparison with those which I have already published concerning the development of Asteroidea and Echinoidea, whilst a number of new and unexpected facts have disclosed themselves which possess interest for a 558 E. W. MAOBRIDE. wider range of students than specialists in the class Echino- dermata. The most interesting result which was obtained from the study of the development of Asteroidea and Bchinoidea was the discovery that the ccelom of the larva showed distinct traces of metameric segmentation, a division into three somites being clearly indicated. The pioneer in this work is Bury, to whose stimulating papers (4, 5, and 6) I wish on this occasion, as formerly, to express my deep indebtedness.
    [Show full text]