Heterogeneous Predator Activity and Implications for Prey Persistence Eric M
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Species List
1 of 16 Claypits 20/09/2021 species list Group Taxon Common Name Earliest Latest Records acarine Aceria macrorhyncha 2012 2012 1 acarine Aceria nalepai 2018 2018 1 amphibian Bufo bufo Common Toad 2001 2018 6 amphibian Lissotriton helveticus Palmate Newt 2001 2018 5 amphibian Lissotriton vulgaris Smooth Newt 2001 2001 1 annelid Hirudinea Leech 2011 2011 1 bird Acanthis cabaret Lesser Redpoll 2013 2013 1 bird Acrocephalus schoenobaenus Sedge Warbler 2001 2011 2 bird Aegithalos caudatus Long-tailed Tit 2011 2014 2 bird Alcedo atthis Kingfisher 2020 2020 1 bird Anas platyrhynchos Mallard 2013 2018 4 bird Anser Goose 2011 2011 1 bird Ardea cinerea Grey Heron 2013 2013 1 bird Aythya fuligula Tufted Duck 2013 2014 1 bird Buteo buteo Buzzard 2013 2014 2 bird Carduelis carduelis Goldfinch 2011 2014 5 bird Chloris chloris Greenfinch 2011 2014 6 bird Chroicocephalus ridibundus Black-headed Gull 2014 2014 1 bird Coloeus monedula Jackdaw 2011 2013 2 bird Columba livia Feral Pigeon 2014 2014 1 bird Columba palumbus Woodpigeon 2011 2018 8 bird Corvus corax Raven 2020 2020 1 bird Corvus corone Carrion Crow 2011 2014 5 bird Curruca communis Whitethroat 2011 2014 4 bird Cyanistes caeruleus Blue Tit 2011 2014 6 bird Cygnus olor Mute Swan 2013 2014 4 bird Delichon urbicum House Martin 2011 2011 1 bird Emberiza schoeniclus Reed Bunting 2013 2014 2 bird Erithacus rubecula Robin 2011 2014 7 bird Falco peregrinus Peregrine 2013 2013 1 bird Falco tinnunculus Kestrel 2010 2020 3 bird Fringilla coelebs Chaffinch 2011 2014 7 bird Gallinula chloropus Moorhen 2013 -

List of UK BAP Priority Terrestrial Invertebrate Species (2007)
UK Biodiversity Action Plan List of UK BAP Priority Terrestrial Invertebrate Species (2007) For more information about the UK Biodiversity Action Plan (UK BAP) visit https://jncc.gov.uk/our-work/uk-bap/ List of UK BAP Priority Terrestrial Invertebrate Species (2007) A list of the UK BAP priority terrestrial invertebrate species, divided by taxonomic group into: Insects, Arachnids, Molluscs and Other invertebrates (Crustaceans, Worms, Cnidaria, Bryozoans, Millipedes, Centipedes), is provided in the tables below. The list was created between 1995 and 1999, and subsequently updated in response to the Species and Habitats Review Report published in 2007. The table also provides details of the species' occurrences in the four UK countries, and describes whether the species was an 'original' species (on the original list created between 1995 and 1999), or was added following the 2007 review. All original species were provided with Species Action Plans (SAPs), species statements, or are included within grouped plans or statements, whereas there are no published plans for the species added in 2007. Scientific names and commonly used synonyms derive from the Nameserver facility of the UK Species Dictionary, which is managed by the Natural History Museum. Insects Scientific name Common Taxon England Scotland Wales Northern Original UK name Ireland BAP species? Acosmetia caliginosa Reddish Buff moth Y N Yes – SAP Acronicta psi Grey Dagger moth Y Y Y Y Acronicta rumicis Knot Grass moth Y Y N Y Adscita statices The Forester moth Y Y Y Y Aeshna isosceles -

Yorkhill Green Spaces Wildlife Species List
Yorkhill Green Spaces Wildlife Species List April 2021 update Yorkhill Green Spaces Species list Draft list of animals, plants, fungi, mosses and lichens recorded from Yorkhill, Glasgow. Main sites: Yorkhill Park, Overnewton Park and Kelvinhaugh Park (AKA Cherry Park). Other recorded sites: bank of River Kelvin at Bunhouse Rd/ Old Dumbarton Rd, Clyde Expressway path, casual records from streets and gardens in Yorkhill. Species total: 711 Vertebrates: Amhibians:1, Birds: 57, Fish: 7, Mammals (wild): 15 Invertebrates: Amphipods: 1, Ants: 3, Bees: 26, Beetles: 21, Butterflies: 11, Caddisflies: 2, Centipedes: 3, Earthworms: 2, Earwig: 1, Flatworms: 1, Flies: 61, Grasshoppers: 1, Harvestmen: 2, Lacewings: 2, Mayflies: 2, Mites: 4, Millipedes: 3, Moths: 149, True bugs: 13, Slugs & snails: 21, Spiders: 14, Springtails: 2, Wasps: 13, Woodlice: 5 Plants: Flowering plants: 174, Ferns: 5, Grasses: 13, Horsetail: 1, Liverworts: 7, Mosses:17, Trees: 19 Fungi and lichens: Fungi: 24, Lichens: 10 Conservation Status: NameSBL - Scottish Biodiversity List Priority Species Birds of Conservation Concern - Red List, Amber List Last Common name Species Taxon Record Common toad Bufo bufo amphiban 2012 Australian landhopper Arcitalitrus dorrieni amphipod 2021 Black garden ant Lasius niger ant 2020 Red ant Myrmica rubra ant 2021 Red ant Myrmica ruginodis ant 2014 Buff-tailed bumblebee Bombus terrestris bee 2021 Garden bumblebee Bombus hortorum bee 2020 Tree bumblebee Bombus hypnorum bee 2021 Heath bumblebee Bombus jonellus bee 2020 Red-tailed bumblebee Bombus -

Most Are Represented in REAL's Butterfly Garden
Butterfly Attracting Perennials and Annuals (Most are represented in REAL’s butterfly garden) Swamp Milkweed Milkweed Weed Tropical milkweed Yarrow (Achillea)- host (asclepias incarnata) (asclepias tuberosa) (Asclepias plant for camouflaged Host plant for Monarch Host plant for Monarch currassavica) loopers, striped garden Host plant for Monarch caterpillars, blackberry loopers, common pugs, cynical quakers, olive arches, and voluble darts Common Boneset Blue False Indigo Black Eyed Susan Tickseed- Coreopsis- (Eupatorium perfoliatum) (Baptisia Australis) (Rudbeckia Hirta) Nectar plant for many Host plant for Burdock Host plant for - Frosted Host Plant for Silvery species of butterflies Borer, Three lined flower Elfin, Orange Sulphur, Checkerspot and moth, Blackberry Looper, Eastern Tailed Blue Gorgone Checkerspot) and Clymene Moth) and Wild Indigo Duskywing, Canadian Skipper Goldenrod, genus Blue Flag Iris- (Iris Common thistle -up Nettle-Urtica dioica - Solidago - Host plant for Vericolore) Height: Likes to 2 metres high- About 2-4 feet tall. asteroid, the brown- wet soil. attract Host to Painted Has stinging hairs along hooded owlet, the hummingbirds, butterflies, Lady the stem. beneficial insects, and Host plant to Red camouflaged looper, the native bees; C Admiral, Milbert’s common pug, the striped Tortoiseshell butterfly garden caterpillar, and the goldenrod gall moth. Pearly everlasting Chokecherry Prunus Dogwood family Asters (genus aster)- host Anaphalis margaritacea — virginiana — ((Cornaceae) host plant for pearl crescents, Host -

Ecological Consequences Artificial Night Lighting
Rich Longcore ECOLOGY Advance praise for Ecological Consequences of Artificial Night Lighting E c Ecological Consequences “As a kid, I spent many a night under streetlamps looking for toads and bugs, or o l simply watching the bats. The two dozen experts who wrote this text still do. This o of isis aa definitive,definitive, readable,readable, comprehensivecomprehensive reviewreview ofof howhow artificialartificial nightnight lightinglighting affectsaffects g animals and plants. The reader learns about possible and definite effects of i animals and plants. The reader learns about possible and definite effects of c Artificial Night Lighting photopollution, illustrated with important examples of how to mitigate these effects a on species ranging from sea turtles to moths. Each section is introduced by a l delightful vignette that sends you rushing back to your own nighttime adventures, C be they chasing fireflies or grabbing frogs.” o n —JOHN M. MARZLUFF,, DenmanDenman ProfessorProfessor ofof SustainableSustainable ResourceResource Sciences,Sciences, s College of Forest Resources, University of Washington e q “This book is that rare phenomenon, one that provides us with a unique, relevant, and u seminal contribution to our knowledge, examining the physiological, behavioral, e n reproductive, community,community, and other ecological effectseffects of light pollution. It will c enhance our ability to mitigate this ominous envirenvironmentalonmental alteration thrthroughough mormoree e conscious and effective design of the built environment.” -

The Moths (Lepidoptera) of Glasgow Botanic Gardens
The Glasgow Naturalist (online 2019) Volume 27, Part 1 The moths (Lepidoptera) of Glasgow Botanic Gardens R.B. Weddle 89 Novar Drive, Glasgow G12 9SS E-mail: [email protected] ABSTRACT At the end of 2018 the species list included 201 distinct The moths that have been recorded in the Glasgow moth species; this may be compared with the 859 moths Botanic Gardens, Scotland over the years are reviewed which had been recorded in Glasgow as a whole at the and assessed in the context of the City of Glasgow, the same date. In this account I shall comment on just a few vice-county of Lanarkshire (VC77), and the U.K. in of those 201 species, which seem to be significant in one general. The additions to the list since the last review in way or another. More detail on any of the records can be 1999 are highlighted. Some rare and endangered species obtained from Glasgow Museums Biological Record are reported, though the comparatively low frequency of Centre, and Scottish distribution maps of the various sightings of several normally common species suggests moths can be found at www.eastscotland- that the site is generally under-recorded. The same is butterflies.org.uk/mothflighttimes.html true of Glasgow and Lanarkshire in general. In the 2017 Bioblitz (including the Bat & Moth Night) INTRODUCTION 15 species of moth were recorded; two of these (rosy There are few records of moths in the Glasgow Botanic rustic and bulrush wainscot) are highlighted in the Gardens (GBG) prior to 1980-1999 when Dr Robin following sections. -

The Orkney Local Biodiversity Action Plan 2013-2016 and Appendices
Contents Page Section 1 Introduction 4 1.1 Biodiversity action in Orkney – general outline of the Plan 6 1.2 Biodiversity Action Planning - the international and national contexts 6 • The Scottish Biodiversity Strategy 1.3 Recent developments in environmental legislation 8 • The Marine (Scotland) Act 2010 • The Wildlife and Natural Environment (Scotland) Act 2011 • The Climate Change (Scotland) Act 2009 1.4 Biodiversity and the Local Authority Planning System 12 • The Orkney Local Development Plan 2012-2017 1.5 Community Planning 13 1.6 River Basin Management Planning 13 1.7 Biodiversity and rural development policy 14 • The Common Agricultural Policy • Scotland Rural Development Programme 2007-2013 1.8 Other relevant national publications 15 • Scotland’s Climate Change Adaptation Framework • Scotland’s Land Use Strategy • The Scottish Soil Framework 1.9 Links with the Orkney Biodiversity Records Centre 16 Section 2 Selection of the Ten Habitats for Inclusion in the Orkney Biodiversity Action Plan 2013-2016 17 1 • Lowland fens 19 2 • Basin bog 27 3 • Eutrophic standing waters 33 4 • Mesotrophic lochs 41 5 • Ponds and milldams 47 6 • Burns and canalized burns 53 7 • Coastal sand dunes and links 60 8 • Aeolianite 70 9 • Coastal vegetated shingle 74 10 • Intertidal Underboulder Communities 80 Appendix I Species considered to be of conservation concern in Orkney Appendix II BAP habitats found in Orkney Appendix III The Aichi targets and goals 3 Orkney Local Biodiversity Action Plan 2013-2016 Section 1 – Introduction What is biodiversity? a) Consider natural systems – by using The term ‘biodiversity’ means, quite simply, knowledge of interactions in nature and how the variety of species and genetic varieties ecosystems function. -

Butterfly Conservation Upper Thames Branch Moth Sightings Archive - July to December 2012
Butterfly Conservation Upper Thames Branch Moth Sightings Archive - July to December 2012 MOTH SPECIES COUNT FOR 2012 = 946 ~ Friday 25th January 2013 ~ Andy King sent the following: "Peter Hall has identified a number of moths for me and just one of them is of particular note for your site: A Coleophora currucipennella flew into my trap on 23 July 2012 at Philipshill Wood, Bucks. This was a small, brownish unprepossessing thing. Its significance is that it was only the second Bucks record for this proposed Red Data Book 3 species. " ~ Tuesday 8th January 2013 ~ 05/01/13 - Dave Wilton sent the following report: "On 5th January Peter Hall completed the final dissections of difficult moths from me for 2012 and the following can now be added to the year list: Maple Pug (Westcott 8th August), Acompsia cinerella (Steps Hill 14th August), Agonopterix nervosa (Calvert 9th September), Anacampsis blattariella (Finemere Wood 19th August), Caryocolum fraternella (Calvert 12th August), Coleophora albitarsella (Westcott 10th August), Coleophora versurella (Ivinghoe Beacon 9th August), Cosmiotes stabilella (Calvert 17th August), Depressaria badiella (Calvert 12th August), Depressaria chaerophylli (Ivinghoe Beacon 3rd September), Depressaria douglasella (Ivinghoe Beacon 3rd August), Monochroa lutulentella (Finemere Wood 1st September), Oegoconia quadripuncta (Ivinghoe Beacon 9th August), Phyllonorycter oxyacanthae (Westcott 18th August), Scoparia basistrigalis (Calvert 12th August), Stigmella obliquella (Finemere Wood 19th August), Stigmella salicis (private wood near Buckingham 20th August) & Stigmella samiatella (Finemere Wood 17th July). Thankyou Peter!" ~ Friday 7th December 2012 ~ Dave Wilton sent this update: "On 20th November here at Westcott, Bucks my garden actinic trap managed Caloptilia rufipennella (1), Acleris schalleriana (1), an as yet unconfirmed Depressaria sp. -

Spatial Synchrony Propagates Through a Forest Food Web Via Consumer-Resource Interactions
Ecology, 90(11), 2009, pp. 2974-2983 © 2009 by the Ecological Society of America Spatial synchrony propagates through a forest food web via consumer-resource interactions KYLE J. HAYNEs, 1•6 ANDREW M. LIEBHOLD, 2 ToDD M. FEARER, 3 Gu1MING WANG,4 GARY W. NoRMAN, 5 AND DEREK M. JoHNSON 1 'Department of Biology, University of Louisiana, P.O. Box 42451, Lafayette, Louisiana 70504 USA 2 USDA Forest Service, Northern Research Station, 180 Canfield Street, Morgantown, West Virginia 26505 USA 3 Arkansas Forest Resources Center, School of Forest Resources, University of Arkansas, P.O. Box 3468, Monticello, Arkansas 71656 USA 4Department of Wildlife and Fisheries, Mississippi State University, Box 9690, Mississippi State, Mississippi 39762 USA 5 Virginia Department of Game and Inland Fisheries, P.O. Box 996, Verona, Virginia 24482 USA Abstract. In many study systems, populations fluctuate synchronously across large regions. Several mechanisms have been advanced to explain this, but their importance in nature is often uncertain. Theoretical studies suggest that spatial synchrony initiated in one species through Moran effects may propagate among trophically linked species, but evidence for this in nature is lacking. By applying the nonparametric spatial correlation function to time series data, we discover that densities of the gypsy moth, the moth's chief predator (the white footed mouse), and the mouse's winter food source (red oak acorns) fluctuate synchronously over similar distances ( ~ 1000 km) and with similar levels of synchrony. In addition, we investigate the importance of consumer-resource interactions in propagating synchrony among species using an empirically informed simulation model of interactions between acorns, the white-footed mouse, the gypsy moth, and a viral pathogen of the gypsy moth. -

Pharmacology and Therapeutics Principles of Clinical Pharmacology and Therapeutics 3
2 Principles of Clinical Pharmacology and Therapeutics Principles of Clinical Pharmacology and Therapeutics 3 and the maximum dosage whereby no toxic symptoms occur is called the therapeutic width. Finally, administration of a substance can also induce a number of effects which have nothing whatsoever to do with the pharmacological properties of the substance; these are the placebo 1 effects. GENERAL PHARMACOLOGY Nomenclature Pharmacology deals with the knowledge of drugs. Drugs are Pharmacology chemical substances which affect living organisms and are used by the clinician to diagnose, prevent or cure diseases. So the safe use of drugs needs sound knowledge of their various aspects such as INTRODUCTION mechanism of action, doses, routes of administration, adverse affects, From the fact mentioned that pharmacon can mean both toxicity, drug interactions etc. medicine and poison, it follows that what we ingest does not always A health professional is also interested to know the chemical result in the desired effect, the primary effect, but can also result in agents that are commonly responsible for household and industrial unwanted side effects on the basis of which we classify that substance poisoning as well as environmental pollution so that he may prevent, as toxic (poisonous). recognize and treat such toxicity or pollution. The primary effect is, therefore, understood to be the desired The word pharmacology is derived from the Greek words effect, the effect intended. Side effects are those effects which are not pharmakon (drug) and logos (study). The word drug has also a French intended, but do occur. Every healing or pleasure substance has side- origin— ‘drouge’ (dry herb). -

2017 Scottish Macro Moth List
SCOTTISH MACRO-MOTH LIST, 2017 Vernacular Name Code Taxon UK Status Scottish status Scottish Trend since 1980 Orange Swift 3.001 Triodia sylvina Common Widespread but local stable Common Swift 3.002 Korscheltellus lupulina Common Common S, scarce or absent N stable Map-winged Swift 3.003 Korscheltellus fusconebulosa Local Common stable Gold Swift 3.004 Phymatopus hecta Local Common stable Ghost Moth 3.005 Hepialus humuli Common Common stable Goat Moth 50.001 Cossus cossus Nb Scarce and very local, mainly Highlands stable? Lunar Hornet Moth 52.003 Sesia bembeciformis Common Widespread but overlooked? decline - G. S. Woodpecker predation? Welsh Clearwing 52.005 Synanthedon scoliaeformis RDB Very local in Highlands stable Large Red-belted Clearwing 52.007 Synanthedon culiciformis Nb Widespread but overlooked? stable Red-tipped Clearwing 52.008 Synanthedon formicaeformis Nb Dumfries & Galloway, last seen in 1942 extinct, or overlooked? Currant Clearwing 52.013 Synanthedon tipuliformis Nb SE only? Still present VC82 in 2014 major decline Thrift Clearwing 52.016 Pyropteron muscaeformis Nb SW & NE coasts, very local stable Forester 54.002 Adscita statices Local Very local, W and SW stable? Transparent Burnet 54.004 Zygaena purpuralis Na Very local, west Highlands stable Slender Scotch Burnet 54.005 Zygaena loti RDB Mull only stable Mountain Burnet 54.006 Zygaena exulans RDB Very local, VC92 stable New Forest Burnet 54.007 Zygaena viciae RDB, protected Very local, W coast fluctuates Six-spot Burnet 54.008 Zygaena filipendulae Common Common but mainly coastal range expansion NW, also inland Narrow-bordered Five-spot Burnet 54.009 Zygaena lonicerae Common SE, spreading; VC73; ssp. -
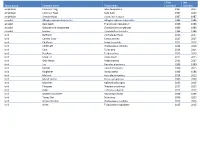
Taxon Group Common Name Taxon Name First Recorded Last
First Last Taxon group Common name Taxon name recorded recorded amphibian Common Frog Rana temporaria 1987 2017 amphibian Common Toad Bufo bufo 1987 2017 amphibian Smooth Newt Lissotriton vulgaris 1987 1987 annelid Alboglossiphonia heteroclita Alboglossiphonia heteroclita 1986 1986 annelid duck leech Theromyzon tessulatum 1986 1986 annelid Glossiphonia complanata Glossiphonia complanata 1986 1986 annelid leeches Erpobdella octoculata 1986 1986 bird Bullfinch Pyrrhula pyrrhula 2016 2017 bird Carrion Crow Corvus corone 2017 2017 bird Chaffinch Fringilla coelebs 2015 2017 bird Chiffchaff Phylloscopus collybita 2014 2016 bird Coot Fulica atra 2014 2014 bird Fieldfare Turdus pilaris 2015 2015 bird Great Tit Parus major 2015 2015 bird Grey Heron Ardea cinerea 2013 2017 bird Jay Garrulus glandarius 1999 1999 bird Kestrel Falco tinnunculus 1999 2015 bird Kingfisher Alcedo atthis 1986 1986 bird Mallard Anas platyrhynchos 2014 2015 bird Marsh Harrier Circus aeruginosus 2000 2000 bird Moorhen Gallinula chloropus 2015 2015 bird Pheasant Phasianus colchicus 2017 2017 bird Robin Erithacus rubecula 2017 2017 bird Spotted Flycatcher Muscicapa striata 1986 1986 bird Tawny Owl Strix aluco 2006 2015 bird Willow Warbler Phylloscopus trochilus 2015 2015 bird Wren Troglodytes troglodytes 2015 2015 bird Yellowhammer Emberiza citrinella 2000 2000 conifer Douglas Fir Pseudotsuga menziesii 2004 2004 conifer European Larch Larix decidua 2004 2004 conifer Lawson's Cypress Chamaecyparis lawsoniana 2004 2004 conifer Scots Pine Pinus sylvestris 1986 2004 crustacean