Design and Analysis of Double Precision Floating Point Division Operator Based on CORDIC Algorithm
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

3.2 the CORDIC Algorithm
UC San Diego UC San Diego Electronic Theses and Dissertations Title Improved VLSI architecture for attitude determination computations Permalink https://escholarship.org/uc/item/5jf926fv Author Arrigo, Jeanette Fay Freauf Publication Date 2006 Peer reviewed|Thesis/dissertation eScholarship.org Powered by the California Digital Library University of California 1 UNIVERSITY OF CALIFORNIA, SAN DIEGO Improved VLSI Architecture for Attitude Determination Computations A dissertation submitted in partial satisfaction of the requirements for the degree Doctor of Philosophy in Electrical and Computer Engineering (Electronic Circuits and Systems) by Jeanette Fay Freauf Arrigo Committee in charge: Professor Paul M. Chau, Chair Professor C.K. Cheng Professor Sujit Dey Professor Lawrence Larson Professor Alan Schneider 2006 2 Copyright Jeanette Fay Freauf Arrigo, 2006 All rights reserved. iv DEDICATION This thesis is dedicated to my husband Dale Arrigo for his encouragement, support and model of perseverance, and to my father Eugene Freauf for his patience during my pursuit. In memory of my mother Fay Freauf and grandmother Fay Linton Thoreson, incredible mentors and great advocates of the quest for knowledge. iv v TABLE OF CONTENTS Signature Page...............................................................................................................iii Dedication … ................................................................................................................iv Table of Contents ...........................................................................................................v -

CORDIC-Like Method for Solving Kepler's Equation
A&A 619, A128 (2018) Astronomy https://doi.org/10.1051/0004-6361/201833162 & c ESO 2018 Astrophysics CORDIC-like method for solving Kepler’s equation M. Zechmeister Institut für Astrophysik, Georg-August-Universität, Friedrich-Hund-Platz 1, 37077 Göttingen, Germany e-mail: [email protected] Received 4 April 2018 / Accepted 14 August 2018 ABSTRACT Context. Many algorithms to solve Kepler’s equations require the evaluation of trigonometric or root functions. Aims. We present an algorithm to compute the eccentric anomaly and even its cosine and sine terms without usage of other transcen- dental functions at run-time. With slight modifications it is also applicable for the hyperbolic case. Methods. Based on the idea of CORDIC, our method requires only additions and multiplications and a short table. The table is inde- pendent of eccentricity and can be hardcoded. Its length depends on the desired precision. Results. The code is short. The convergence is linear for all mean anomalies and eccentricities e (including e = 1). As a stand-alone algorithm, single and double precision is obtained with 29 and 55 iterations, respectively. Half or two-thirds of the iterations can be saved in combination with Newton’s or Halley’s method at the cost of one division. Key words. celestial mechanics – methods: numerical 1. Introduction expansion of the sine term and yielded with root finding methods a maximum error of 10−10 after inversion of a fifteen-degree Kepler’s equation relates the mean anomaly M and the eccentric polynomial. Another possibility to reduce the iteration is to use anomaly E in orbits with eccentricity e. -

CORDIC V6.0 Logicore IP Product Guide
CORDIC v6.0 LogiCORE IP Product Guide Vivado Design Suite PG105 August 6, 2021 Table of Contents IP Facts Chapter 1: Overview Navigating Content by Design Process . 5 Core Overview . 5 Feature Summary. 6 Applications . 6 Licensing and Ordering . 7 Chapter 2: Product Specification Performance. 8 Resource Utilization. 9 Port Descriptions . 9 Chapter 3: Designing with the Core Clocking. 12 Resets . 12 Protocol Description – AXI4-Stream . 12 Functional Description. 17 Input/Output Data Representation . 30 Chapter 4: Design Flow Steps Customizing and Generating the Core . 38 System Generator for DSP. 44 Constraining the Core . 44 Simulation . 45 Synthesis and Implementation . 46 Chapter 5: C Model Features . 47 Overview . 47 Installation . 48 C Model Interface. 49 CORDIC v6.0 Send Feedback 2 PG105 August 6, 2021 www.xilinx.com Compiling . 53 Linking. 53 Dependent Libraries . 54 Example . 55 Chapter 6: Test Bench Demonstration Test Bench . 56 Appendix A: Upgrading Migrating to the Vivado Design Suite. 58 Upgrading in the Vivado Design Suite . 58 Appendix B: Debugging Finding Help on Xilinx.com . 62 Debug Tools . 63 Simulation Debug. 64 AXI4-Stream Interface Debug . 65 Appendix C: Additional Resources and Legal Notices Xilinx Resources . 66 Documentation Navigator and Design Hubs . 66 References . 67 Revision History . 67 Please Read: Important Legal Notices . 68 CORDIC v6.0 Send Feedback 3 PG105 August 6, 2021 www.xilinx.com IP Facts Introduction LogiCORE IP Facts Table Core Specifics This Xilinx® LogiCORE™ IP core implements a Versal™ ACAP -

A Review on Hardware Accelerator Design and Implementation of CORDIC Algorithm for a Gaming Application
International Journal of Innovative Technology and Exploring Engineering (IJITEE) ISSN: 2278-3075, Volume-9 Issue-9, July 2020 A Review on Hardware Accelerator Design and Implementation of CORDIC Algorithm for a Gaming Application Trupthi B, Jalendra H E, Srilaxmi C P, Varun M S, Geethashree A Abstract - Co-ordinate Digital rotation computer is the full The conversion of rectangular to polar and polar to form of CORDIC.CORDIC is a process for finding functions rectangular function are the two major operations in using less hardware like shifts, subs/adds and then compares. It's CORDIC. Basically, they are the two different co-ordinates the algorithm used for some elementary functions which are calculated in real-time and many conversions like from to represent the 2D plane. The Rectangular form is rectangular to polar co-ordinate and vice versa. Rectangular to represented by a real part (horizontal axis) and an imaginary polar and polar to rectangular is an important operation in (Vertical axis) part of the vector. The Rectangular form is CORDIC which are generally used in ALUs, wireless shown by a real part (horizontal axis) and an imaginary communications, DSP processors etc. This paper proposes the (Vertical axis) part of the vector [8].The rectangular co- implementation of physical design for CORDIC algorithm for ordinates are in the form of (x, y) where „x‟ stands for a polar to rectangular and rectangular to polar conversions, by the use of RTL code in written in Verilog and fed to pre-processor, horizontal plane and „y‟ stands for the vertical plane from cordic core and post processor. -

A.1 CORDIC Algorithm
Research on Hardware Intellectual Property Cores Based on Look-Up Table Architecture for DSP Applications HOANG VAN PHUC Doctoral Program in Electronic Engineering Graduate School of Electro-Communications The University of Electro-Communications A thesis submitted for the degree of DOCTOR OF ENGINEERING September 2012 I would like to dedicate this dissertation to my parents, my wife and my daughter. Research on Hardware Intellectual Property Cores Based on Look-Up Table Architecture for DSP Applications APPROVED Asso. Prof. Cong-Kha PHAM, Chairman Prof. Kazushi NAKANO Prof. Yoshinao MIZUGAKI Prof. Koichiro ISHIBASHI Asso. Prof. Takayuki NAGAI Date Approved by Chairman c Copyright 2012 by HOANG Van Phuc All Rights Reserved. 和文要旨 DSPアプリケーションのためのルックアップテーブルアーキテ クチャに基づくハードウェアIPコアに関する研究 ホアン ヴァンフック 電気通信学研究科電子工学専攻博士後期課程 電気通信大学大学院 本論文は,ルックアップテーブル(LUT)アーキテクチャに基づく省面積 かつ高性能なハードウェア IP コアを提案し,DSP アプリケーションに適用 することを目的としている.LUT ベースの IP コアおよびこれらに基づいた 新しい計算システムを提案した.ここで,提案する計算システムには,従来 の演算と提案する IP コアを含む.提案する IP コアには,乗算や二乗計算等 の基本演算と,正弦関数や対数・真数計算等の初等関数が含まれる. まず初めに,高効率な LUT 乗算器および二乗回路の設計を目的として, 2つの方法を提案した.1つは,全幅結果が不要な場合に DSP に応用可能 な打切り定数乗算器である.このアーキテクチャには,LUT ベースの計算と DSP 用の打切り定数乗算器という2つのアプローチを組み合わせた.最適な パラメータと LUT の内容を探索するために,LUT 最適化アルゴリズムの検 討を行った.さらに,固定幅二乗回路向けに LUT ハイブリッドアーキテク チャを改良した.この技術は,二乗回路における性能,誤計算率,複雑さの 間の妥協点を見いだすために,LUT 論理回路と従来の論理回路の両方を採用 したものである. 初等関数の計算については,LUT ベースの計算と線形差分法を組み合わせ て,2つのアーキテクチャを提案した.1つは,ディジタル周波数合成器, 適応信号処理技術および正弦関数生成器に利用可能な正弦関数計算のために, 線形差分法を改良したものである.他の方法と比較して誤計算率が変わらな い一方で,LUT の規模と複雑さを抑える最適パラメータを探索するために数 値解析と最適化を行った.その他に,対数計算および真数計算向けに,疑似 -

An Optimization of CORDIC Algorithm and FPGA Implementation
International Journal of Hybrid Information Technology Vol.8, No.6 (2015), pp.217-228 http://dx.doi.org/10.14257/ijhit.2015.8.6.21 An Optimization of CORDIC Algorithm and FPGA Implementation Rui Xua, Zhanpeng Jiangb, Hai Huangc, Changchun Dongd Department of Integrated circuits design and integrated systems,Harbin University of Science and Technology ,Harbin, Heilongjiang, China [email protected], b [email protected], [email protected] [email protected] Abstract ASIC and FPGA ASIC and FPGA are considered to be the ideal platform for special fast calculations because of the hardware structure, and how to achieve computational algorithm by is the hotpot of research. The CORDIC (Coordinate Rotational Digital Computer) can break the basis functions down to operations of shift and addition or subtraction, which can be used to lay the foundation for the realization of complex logic. But the functions selected by traditional CODIC for angle encoding are too complex, which will lead to some problems, such as too much of area consumption and large delay. In this paper, an optimization of CORDIC algorithm are proposed, which reduce the consumption of Adders and comparators, decrease the complexity and delay of the algorithm implement in hardware. The proposed algorithms are modeled in Verilog Hardware Description Language and implemented with FPGA. The simulation results show that the functions of sine and cosine are realized successfully, and the proposed algorithm not only improves the computation speed but also reduces -

FPGA Technology in Beam Instrumentation and Related Tools
FPGA technology in beam instrumentation and related tools Javier Serrano CERN, Geneva, Switzerland DIPAC 2005. Lyon, France. 7 June 2005. Plan of the presentation z FPGA architecture basics z FPGA design flow z Performance boosting techniques z Doing arithmetic with FPGAs z Example: RF cavity control in CERN’s Linac 3. DIPAC 2005. Lyon, France. 7 June 2005. A preamble: basic digital design Clk [31:0] DataInB[31:0] [31:0] D[31:0] Q[31:0] [31:0] D[0] Q[0] [31:0] 0 dataBC[31:0] dataSelectC [31:0] [31:0] [31:0] D[31:0] Q[31:0] [31:0] DataOut[31:0] DataSelect [31:0] 1 DataOut[31:0] DataOut_3[31:0] [31:0] High clock rate: [31:0] + [31:0] sum[31:0] DataInA[31:0] [31:0] D[31:0] Q[31:0] 144.9 MHz on a [31:0] [31:0] 6.90 ns dataAC[31:0] Xilinx Spartan IIE. DataSelect D[0] Q[0] D[0] Q[0] dataSelectC dataSelectCD1 Clk [31:0] D[31:0] Q[31:0] [31:0] 0 [31:0] [31:0] [31:0] [31:0] DataInB[31:0] [31:0] D[31:0] Q[31:0] [31:0] [31:0] D[31:0] Q[31:0] [31:0] DataOut[31:0] dataACd1[31:0] [31:0] 1 dataBC[31:0] DataOut[31:0] DataOut_3[31:0] Higher clock rate: [31:0] [31:0] + [31:0] D[31:0] Q[31:0] [31:0] DataInA[31:0] [31:0] D[31:0] Q[31:0] [31:0] 151.5 MHz on the [31:0] [31:0] sum_1[31:0] sum[31:0] dataAC[31:0] 6.60 ns same chip. -

A Unified Reconfigurable CORDIC Processor for Floating-Point Arithmetic
Preprints (www.preprints.org) | NOT PEER-REVIEWED | Posted: 25 June 2018 doi:10.20944/preprints201806.0393.v1 Article A Unified Reconfigurable CORDIC Processor for Floating-Point Arithmetic Linlin Fang 1, Bingyi Li 1, Yizhuang Xie 1,* and He Chen 1 1 Beijing Key Laboratory of Embedded Real-time Information Processing Technology, Beijing Institute of Technology, Beijing 100081, China; [email protected] (L.F.); [email protected] (B.L.); [email protected] (Y.X.); [email protected] (H.C.) * Correspondence: [email protected]; Tel.: +86-156-5279-7282 Abstract: This paper presents a unified reconfigurable coordinate rotation digital computer (CORDIC) processor for floating-point arithmetic. It can be configured to operate in multi-mode to achieve a variety of operations and replaces multiple single-mode CORDIC processors. A reconfigurable pipeline-parallel mixed architecture is proposed to adapt different operations, which maximizes the sharing of common hardware circuit and achieves the area-delay-efficiency. Compared with previous unified floating-point CORDIC processors, the consumption of hardware resources is greatly reduced. As a proof of concept, we apply it to 16384 16384 points target Synthetic Aperture Radar (SAR) imaging system, which is implemented on Xilinx XC7VX690T FPGA platform. The maximum relative error of each phase function between hardware and software computation and the corresponding SAR imaging result can meet the accuracy index requirements. Keywords: reconfigurable architecture; CORDIC; Field Programmable Gate Array(FPGA); SAR imaging 1. Introduction The CORDIC algorithm involves a simple shift-and-add iterative procedure to perform several computing tasks. It can execute the rotation of a two-dimensional (2-D) vector in linear, circular, and hyperbolic coordinates systems [1]. -
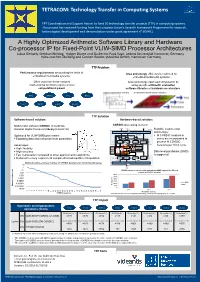
A Highly Optimized Arithmetic Software Library and Hardware Co
TETRACOM: Technology Transfer in Computing Systems FP7 Coordination and support action to fund 50 technology transfer projects (TTP) in computing systems. FP7 Coordination and Support Action to fund 50 technology transfer projects (TTP) in computing systems. This project has received funding from the European Union’s Seventh Framework Programme for research, This project has received funding from the European Union’s Seventh Framework Programme for research, technological development and demonstration under grant agreement n⁰ 609491. technological development and demonstration under grant agreement n⁰ 609491. A Highly Optimized Arithmetic Software Library and Hardware Co-processor IP for Fixed-Point VLIW-SIMD Processor Architectures Lukas Gerlach, Stephan Nolting, Holger Blume and Guillermo Payá Vayá, Leibniz Universität Hannover, Germany Hans‐Joachim Stolberg and Carsten Reuter, videantis GmbH, Hannover, Germany TTP Problem Performance requirements are pushing the limits of Area and energy efficiency is restricted for embedded multimedia systems: embedded multimedia systems: Often used non-linear complex Area and energy optimized computation by mathematical functions require a lot of using specific arithmetic evaluation computational power. software libraries or hardware accelerators. sin() atan() ln() div() cos() sqrt() exp() pow() TTP Solution Software-based solution: Hardware-based solution: Mathematic software CORDIC (Coordinate CORDIC processing element config x,y,z start Rotation Digital Computer) library (LibARITH) N optional Scalable co-processor Pre-processing stage architecture: Optimized for VLIW-SIMD processors: scale . M CORDIC modules in . Exploiting data and instruction level parallelism series are incorporated to Register Register Register Iteration controller process M CORDIC Advantages: D S iterations per clock cycle CORDIC Scale factor M table . High flexibility Angle P P table P . -

A Trigonometric Hardware Acceleration in 32-Bit RISC-V
This article has been accepted and published on J-STAGE in advance of copyediting. Content is final as presented. IEICE Electronics Express, Vol.VV, No.NN, 1–6 LETTER A Trigonometric Hardware Acceleration in 32-bit RISC-V Microcontroller with Custom Instruction Khai-Duy Nguyen1a), Dang Tuan Kiet1b), Trong-Thuc Hoang1c), Nguyen Quang Nhu Quynh2d), Xuan-Tu Tran3e), and Cong-Kha Pham1f) Abstract This work presents a 32-bit Reduced Instruction Set Computer Nowadays, computational tasks have become far more com- fifth-generation (RISC-V) microprocessor with a COordinate Rotation plex than the way general-purpose computers can serve DIgital Computer (CORDIC) accelerator. The accelerator is implemented them. Thus, processor efficiency requirements are beco- inside the core and being used by the software via custom instruction. The used microprocessor is the VexRiscv with the Instruction Set Architecture ming increasingly critical. Accelerators are extensively used (ISA) of RV32IM; that means 32-bit RISC-V including Integer and for many intensive computational tasks, reducing execution Multiplication. The experimental results were collected using Field- time and energy consumption. Different companies and re- Programmable Gate Array (FPGA) on the DE2-115 development kit and search groups are developing accelerators in RISC-V for Application Specific Integrated Chip (ASIC) synthesizer on 180-nm CMOS various applications such as digital signal processing [7], process library. key words: 32-bit microprocessor, accelerator, CORDIC, custom artificial intelligence [8, 9], and solving mathematical algo- instruction, RISC-V, trigonometric. rithms [10, 11]. Classification: Integrated circuits (logic) Among heavy computational tasks, the calculation of trigo- nometric functions is widely used, especially in digital signal 1. -

Cordic Algorithm and Its Applications In
CORDIC ALGORITHM AND ITS APPLICATIONS IN DSP A THESIS SUBMITTED IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR THE DEGREE OF Bachelor of Technology in Electrical Engineering By SAMBIT KUMAR DASH JASOBANTA SAHOO SUNITA PATEL Department of Electrical Engineering National Institute of Technology Rourkela 2007 1 CORDIC ALGORITHM AND ITS APPLICATIONS IN DSP A THESIS SUBMITTED IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR THE DEGREE OF Bachelor of Technology in Electrical Engineering By SAMBIT KUMAR DASH JASOBANTA SAHOO SUNITA PATEL Under the Guidance of Prof. S. Mohanty Department of Electrical Engineering National Institute of Technology Rourkela 2007 2 National Institute of Technology Rourkela CERTIFICATE This is to certify that the thesis entitled,” CORDIC Algorithm and it’s applications in DSP ” submitted by Sri Sambit Kumar Dash , Sri Jasobanta Sahoo, Sunita Patel in partial fulfillment of the requirements for the award of Bachelor of Technology Degree in Electrical Engineering at the National Institute of Technology, Rourkela (Deemed University) is an authentic work carried out by him under my supervision and guidance. To the best of my knowledge, the matter embodied in the thesis has not been submitted to any other University/Institute for the award of any Degree or Diploma. Date : 02/05/07 Prof. S. Mohanty Place: Rourkela Dept. of Electrical Engg. National Institute of technology Rourkela-769008 3 ACKNOWLEDGEMENT I would like to articulate my deep gratitude to my project guide Prof. S. Mohanty who has always been my motivation for carrying out the project. I wish to extend my sincere thanks to Prof. P. K. Nanda , Head of our Department, for allowing us to use the facilities of the “Computing and Simulation Lab” It is my pleasure to refer Microsoft Word exclusive of which the compilation of this report would have been impossible. -

CORDIC-Based LMMSE Equalizer for Software Defined Radio
CORDIC-Based LMMSE Equalizer for Software Defined Radio Murugappan SENTHILVELAN † §, Javier HORMIGO ‡, Joon Hwa CHUN €, Mihai SIMA *, Daniel IANCU †¶, Michael SCHULTE §, John GLOSSNER ¥ †Optimum Semiconductor Technologies, Inc., Tarrytown, NY, U.S.A. ‡ University of Malaga, Department of Computer Architecture, Malaga, Spain. € Intelligent Automation Inc., Rockville, MD, U.S.A. * University of Victoria, Department of Electrical and Computer Engineering, Victoria, BC, Canada. § University of Wisconsin-Madison, Department of Electrical and Computer Engineering, Madison, WI, U.S.A. ¶ Tampere University of Technology, Korkeakoulunkatu 1, FIN-33720 Tampere, Finland. ¥ Sandbridge Technologies, Inc., Tarrytown, NY, U.S.A. e-mail: [email protected], [email protected], [email protected] [email protected], [email protected], [email protected], [email protected] Abstract — In Code Division Multiple Access (CDMA) interference, and with synchronized transmission of blocks systems, the orthogonality of the spreading codes used to over the channel, multiple users can be multiplexed over the achieve multiple access over a channel is severely degraded same channel by using a different spreading code for each due to multi-path interference. Expensive equalization user. Even though signals from multiple users interfere with techniques are needed to recover the transmitted signal. each other in the channel, due to the orthogonal spreading The Linear Minimum Mean Square Error (LMMSE) codes, each user can extract the transmission intended for equalizer is a sub-optimal equalizer that is a good them from the received signal by despreading it using their compromise between computational complexity and spreading code. communication system performance. It uses While the spreading codes are perfectly orthogonal to computationally-intensive matrix inversion operations to each other, they are not orthogonal to time-shifted versions of perform equalization.