Coupled Cluster Valence Bond Theory for Open-Shell Systems with Application to Very Long Range Strong Correlation in a Polycarbene Dimer
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Proton Nmr Spectroscopy
1H NMR Spectroscopy (#1c) The technique of 1H NMR spectroscopy is central to organic chemistry and other fields involving analysis of organic chemicals, such as forensics and environmental science. It is based on the same principle as magnetic resonance imaging (MRI). This laboratory exercise reviews the principles of interpreting 1H NMR spectra that you should be learning right now in Chemistry 302. There are four questions you should ask when you are trying to interpret an NMR spectrum. Each of these will be discussed in detail. The Four Questions to Ask While Interpreting Spectra 1. How many different environments are there? The number of peaks or resonances (signals) in the spectrum indicates the number of nonequivalent protons in a molecule. Chemically equivalent protons (magnetically equivalent protons) give the same signal in the NMR whereas nonequivalent protons give different signals. 1 For example, the compounds CH3CH3 and BrCH2CH2Br all have one peak in their H NMR spectra because all of the protons in each molecule are equivalent. The compound below, 1,2- dibromo-2-methylpropane, has two peaks: one at 1.87 ppm (the equivalent CH3’s) and the other at 3.86 ppm (the CH2). 1.87 1.87 ppm CH 3 3.86 ppm Br Br CH3 1.87 ppm 3.86 10 9 8 7 6 5 4 3 2 1 0 2. How many 1H are in each environment? The relative intensities of the signals indicate the numbers of protons that are responsible for individual signals. The area under each peak is measured in the form of an integral line. -

Nicolas Namoradze Honens Prize Laureate Chamber Music / Works for Piano & Voice
NICOLAS NAMORADZE HONENS PRIZE LAUREATE CHAMBER MUSIC / WORKS FOR PIANO & VOICE K. Agócs Immutable Dreams (quintet) Bartók Piano Quintet Beethoven Sonata for Piano and Violin in A Major Op. 12 No. 2 Quintet for Piano and Winds Op. 16 Sonata for Piano and Horn in F Major Op. 17 Sonata for Piano and Violin in F Major Op. 24 Sonata for Piano and Cello in A Major Op. 69 Sonata for Piano and Cello in D Major Op. 102 No. 2 Brahms Piano Trio in B Major Op. 8 Piano Quartet in G minor Op. 25 selections from Waltzes Op. 39 Sonata for Piano and Violin in G Major Op. 78 Sonata for Piano and Cello in F Major Op. 99 Piano Trio in C minor Op. 101 Britten Gemini Variations for flute, violin and piano four-hands (Secondo) Cartan Introduction et Allegro for Piano and Wind Quintet Castiglioni Quickly—Variations for Chamber Ensemble Copland Appalachian Spring (chamber version for 13 players) Why do the shut me out of heaven? (voice and piano) Danzon Cubano (Piano I) Rodeo Hoe-Down (Piano I) Debussy Sonata for Piano and Violin L. 140 La Mer (transcription for piano four-hands / Secondo) Jeux (transcription for two pianos: Roques / Primo) Petite Suite (Secondo) Prélude à l’après-midi d’une faune (transcription for two pianos / Piano I) Prélude à l’après-midi d’une faune (transcription for piano four-hands: Ravel / Secondo) Danses sacrée et profane (transcription for two pianos / Piano II) Dvorak selections from Slavonic Dances Opp. 46 & 72 Dohnányi selections from Ruralia Hungarica Op. -

Spectralism in the Saxophone Repertoire: an Overview and Performance Guide
NORTHWESTERN UNIVERSITY Spectralism in the Saxophone Repertoire: An Overview and Performance Guide A PROJECT DOCUMENT SUBMITTED TO THE BIENEN SCHOOL OF MUSIC IN PARTIAL FULFILLMENT OF THE REQUIREMENTS for the degree DOCTOR OF MUSICAL ARTS Program of Saxophone Performance By Thomas Michael Snydacker EVANSTON, ILLINOIS JUNE 2019 2 ABSTRACT Spectralism in the Saxophone Repertoire: An Overview and Performance Guide Thomas Snydacker The saxophone has long been an instrument at the forefront of new music. Since its invention, supporters of the saxophone have tirelessly pushed to create a repertoire, which has resulted today in an impressive body of work for the yet relatively new instrument. The saxophone has found itself on the cutting edge of new concert music for practically its entire existence, with composers attracted both to its vast array of tonal colors and technical capabilities, as well as the surplus of performers eager to adopt new repertoire. Since the 1970s, one of the most eminent and consequential styles of contemporary music composition has been spectralism. The saxophone, predictably, has benefited tremendously, with repertoire from Gérard Grisey and other founders of the spectral movement, as well as their students and successors. Spectral music has continued to evolve and to influence many compositions into the early stages of the twenty-first century, and the saxophone, ever riding the crest of the wave of new music, has continued to expand its body of repertoire thanks in part to the influence of the spectralists. The current study is a guide for modern saxophonists and pedagogues interested in acquainting themselves with the saxophone music of the spectralists. -
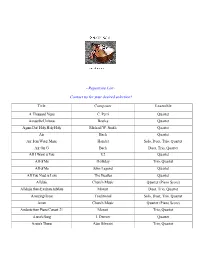
Repertoire List~
~Repertoire List~ Contact us for your desired selection! Title Composer Ensemble A Thousand Years C. Perri Quartet Across the Universe Beatles Quartet Agnus Dei/Holy Holy Holy Michael W. Smith Quartet Air Bach Quartet Air from Water Music Handel Solo, Duet, Trio, Quartet Air On G Bach Duet, Trio, Quartet All I Want is You U2 Quartet All of Me Holliday Trio, Quartet All of Me John Legend Quartet All You Need is Love The Beatles Quartet Alleluia Church Music Quartet (Piano Score) Allelujia from Exultate Jubilate Mozart Duet, Trio, Quartet Amazing Grace Traditional Solo, Duet, Trio, Quartet Amen Church Music Quartet (Piano Score) Andante from Piano Concert 21 Mozart Trio, Quartet Annie’s Song J. Denver Quartet Annie’s Theme Alan Silvestri Trio, Quartet Apollo 13 Horner Quartet Appalachia Waltz O’Connor Trio, Quartet Arioso Bach Solo, Duet, Trio, Quartet Arrival of the Queen of Sheba Handel Trio, Quartet Ashokan Farewell Jay Ungar Quartet (Piano Score) At Last Harry Warren Quartet Ave Maria Bach-Gounod Solo, Duet, Trio, Quartet Ave Maria (A flat) Schubert Quartet (Piano Score) Ave Maria (B flat) Schubert Quartet Ave Verum Corpus Mozart Solo, Duet, Trio, Quartet (plus Piano Score) Barcarolle from Tales of Hoffman Offenbach Quartet Be Thou My Vision Traditional Duet, Trio, Quartet Beauty and the Beast Ashman Quartet Bei Mennern from The Magic Flute Mozart Quartet Best Day of My life American Authors Quartet Bist du bei mer Bach Trio, Quartet Bittersweet Symphony M. Jagger Quartet Blessed are They Church Music Quartet Blessed are Those Who Love You Haugen Quartet (Piano Score) Blue Moon Rodgers Quartet Born Free Barry Quartet Bourree Bach Solo, Duet, Trio, Quartet Bourree Handel Solo, Duet, Trio, Quartet Brandenburg Concerto No. -

Understanding Music Past and Present
Understanding Music Past and Present N. Alan Clark, PhD Thomas Heflin, DMA Jeffrey Kluball, EdD Elizabeth Kramer, PhD Understanding Music Past and Present N. Alan Clark, PhD Thomas Heflin, DMA Jeffrey Kluball, EdD Elizabeth Kramer, PhD Dahlonega, GA Understanding Music: Past and Present is licensed under a Creative Commons Attribu- tion-ShareAlike 4.0 International License. This license allows you to remix, tweak, and build upon this work, even commercially, as long as you credit this original source for the creation and license the new creation under identical terms. If you reuse this content elsewhere, in order to comply with the attribution requirements of the license please attribute the original source to the University System of Georgia. NOTE: The above copyright license which University System of Georgia uses for their original content does not extend to or include content which was accessed and incorpo- rated, and which is licensed under various other CC Licenses, such as ND licenses. Nor does it extend to or include any Special Permissions which were granted to us by the rightsholders for our use of their content. Image Disclaimer: All images and figures in this book are believed to be (after a rea- sonable investigation) either public domain or carry a compatible Creative Commons license. If you are the copyright owner of images in this book and you have not authorized the use of your work under these terms, please contact the University of North Georgia Press at [email protected] to have the content removed. ISBN: 978-1-940771-33-5 Produced by: University System of Georgia Published by: University of North Georgia Press Dahlonega, Georgia Cover Design and Layout Design: Corey Parson For more information, please visit http://ung.edu/university-press Or email [email protected] TABLE OF C ONTENTS MUSIC FUNDAMENTALS 1 N. -

Even String Quartets— No Longer Sit in Chairs When
It’s not a huge FINE, auprising, but a number of Upst ensembles—nding even string quartets— no longer sit in chairs when EMPIRE BRASS performing. What’s it all about? 26 may/june 2010 a ENSEMBLES ike most art forms, chamber music PROS by Judith Kogan performance has evolved to reflect For many people, it’s simply more com- Upst ndingchanges in society and technology. fortable to play standing up. It’s how we’re L As instruments developed greater power to taught to play and how we perform as solo- project, performances moved from small ists. Standing, it’s easier to establish good chambers to larger spaces, where professional posture with the instrument. musicians played to paying audiences. New Standing also allows freedom to express instrumentations, such as the saxophone with the whole body. With arms, shoulders quartet and the percussion ensemble, and waist liberated, a player’s range of motion emerged. By the late twentieth century, expands. For wind players, there’s better composers had recast what was once thought air flow. The ability to turn the whole body of as “intimate musical conversation” to in- makes it easier to communicate with other corporate abrasive electronically-produced ensemble members and the audience. One sonorities. Some works called for musi- arguably feels the rhythm of a piece better cians to wear headphones with click tracks, on one’s feet, and, perhaps unconsciously, preventing them from hearing each other. produces a bigger, fatter sound. Sometimes they couldn’t even hear them- In terms of acoustics, sound travels farther selves. -

Americanensemble
6971.american ensemble 6/14/07 2:02 PM Page 12 AmericanEnsemble Peter Serkin and the Orion String Quartet, Tishman Auditorium, April 2007 Forever Trivia question: Where Julius Levine, Isidore Cohen, Walter Trampler and David Oppenheim performed did the 12-year-old with an array of then-youngsters, including Richard Goode, Richard Stoltzman, Young Peter Serkin make his Ruth Laredo, Lee Luvisi, Murray Perahia, Jaime Laredo and Paula Robison. New York debut? The long-term viability of the New School’s low-budget, high-star-power series (Hint: The Guarneri, is due to several factors: an endowment seeded by music-loving philanthropists Cleveland, Lenox and such as Alice and Jacob Kaplan; the willingness of the participants to accept modest Vermeer string quartets made their first fees; and, of course, the New School’s ongoing generosity in providing a venue, New York appearances in the same venue.) gratis. In addition, Salomon reports, “Sasha never accepted a dime” during his 36 No, not Carnegie Recital Hall. Not the years of labor as music director or as a performer (he played in most of the 92nd Street Y, and certainly not Alice Tully concerts until 1991, two years before his death). In fact, Sasha never stopped Hall (which isn’t old enough). New Yorkers giving—the bulk of his estate went to the Schneider Foundation, which continues first heard the above-named artists in to help support the New School’s chamber music series and Schneider’s other youth- Tishman Auditorium on West 12th Street, at oriented project, the New York String Orchestra Seminar. -

Guide to Repertoire
Guide to Repertoire The chamber music repertoire is both wonderful and almost endless. Some have better grips on it than others, but all who are responsible for what the public hears need to know the landscape of the art form in an overall way, with at least a basic awareness of its details. At the end of the day, it is the music itself that is the substance of the work of both the performer and presenter. Knowing the basics of the repertoire will empower anyone who presents concerts. Here is a run-down of the meat-and-potatoes of the chamber literature, organized by instrumentation, with some historical context. Chamber music ensembles can be most simple divided into five groups: those with piano, those with strings, wind ensembles, mixed ensembles (winds plus strings and sometimes piano), and piano ensembles. Note: The listings below barely scratch the surface of repertoire available for all types of ensembles. The Major Ensembles with Piano The Duo Sonata (piano with one violin, viola, cello or wind instrument) Duo repertoire is generally categorized as either a true duo sonata (solo instrument and piano are equal partners) or as a soloist and accompanist ensemble. For our purposes here we are only discussing the former. Duo sonatas have existed since the Baroque era, and Johann Sebastian Bach has many examples, all with “continuo” accompaniment that comprises full partnership. His violin sonatas, especially, are treasures, and can be performed equally effectively with harpsichord, fortepiano or modern piano. Haydn continued to develop the genre; Mozart wrote an enormous number of violin sonatas (mostly for himself to play as he was a professional-level violinist as well). -

Memorandum LIBRARY of CONGRESS
UNITED STATES GOVERNMENT Memorandum LIBRARY OF CONGRESS 5JSC/LC/12 TO: Joint Steering Committee for Development of RDA DATE: February 6, 2008 FROM: Barbara B. Tillett, LC Representative SUBJECT: Proposed revision of RDA chap. 6, Additional instructions for musical works and expressions The Library of Congress is submitting rule revision proposals for the RDA December 2007 draft chapter 6 instructions for musical works and expressions. Goals of proposals 1. To maintain the additional instructions for music intact (although LC recommends integrating them with the general instructions after the first release of RDA). 2. To fill in gaps in the AACR2 rules carried over into RDA by a. Incorporating selected AACR2 rule revisions; b. Adding instructions that clarify, make explicit, or expand some principles and instructions carried over from AACR2; c. Proposing new instructions. 3. To simplify some unnecessarily complex instructions. 4. To arrange certain subsections in the six major instructions in a more logical way, based wherever possible on principles that group together types of resources having common characteristics. 5. To revise the instructions for medium of performance to provide for all media found in resources and to do that using vocabulary that adheres as closely as possible to the principle of representation: incorporating words the composer or resource uses. 6. To revise or eliminate instructions LC finds unworkable based on past experience with AACR2 (e.g., the instructions for key (6.22) in section M of this document). 7. In the interest of simplification, to eliminate vexing terms catalogers have spent inordinate amounts of time interpreting when using AACR2 (e.g., “type of composition” as a formal term when all it need be is a useful phrase; “score order”). -

Tesla Quartet
TESLA QUARTET R O S S S NYD E R & M I C H E L L E L IE, V I O L I N S – E D W I N K APLAN , V I O L A – S E R A F I M S MIGELSKIY, CELLO 412.952.8676 • [email protected] • www.teslaquartet.com Repertoire * Tesla Quartet commission/premiere String Quartets Elliott Bark Tango Suite Bartók String Quartet No.2, Sz.67 (Op.17) String Quartet No.4, Sz.91 String Quartet No.6, Sz.114 Romanian Folk Dances (arr. Snyder) Beethoven String Quartet in G, Op.18 No.2 String Quartet in B-flat, Op.18 No.6 String Quartet in F, Op.59 No.1 String Quartet in C, Op.59 No.3 String Quartet in F, Op.135 Matthew Browne Great Danger, Keep Out* Brett Dean Eclipse Debussy String Quartet in G minor, Op.10 Dutilleux Ainsi la nuit Dvořák String Quartet No.12 in F, Op.96, “American” String Quartet No.14 in A-flat, Op.105 Erberk Eryılmaz Miniatures Set No.4 Haydn String Quartet in C, Op.20 No.2 String Quartet in D, Op.20 No.4 String Quartet in B minor, Op.33 No.1 String Quartet in G, Op.33 No.5 String Quartet in G, Op.76 No.1 String Quartet in B-flat, Op.76 No.4, “Sunrise” String Quartet in D, Op.76 No.5 Janáček String Quartet No.1, “The Kreutzer Sonata” TESLA QUARTET R O S S S NYD E R & M I C H E L L E L IE, V I O L I N S – E D W I N K APLAN , V I O L A – S E R A F I M S MIGELSKIY, CELLO 412.952.8676 • [email protected] • www.teslaquartet.com Daniel Kellogg “Soft Sleep Shall Contain You” Ligeti Andante and Allegretto Gabriel Lubell A Study of Luminous Objects: String Quartet No.1 Albéric Magnard String Quartet, Op.16 Mendelssohn String Quartet in A minor, Op.13 -

Music 130-205 Piano Ensemble
Music 130-205: Chamber Music Workshop Piano (Piano Ensemble) Syllabus – Spring 2013 Director: Pamela Cordle My Office: CAB-1038 Telephone: (910) 392-2721 Email: [email protected] Class Time: Tuesdays and Thursdays, 5:00-6:15 pm Class Location: CAB-1019 (piano lab) Class meets initially in the digital piano lab. We move into practice rooms as needed. Our Goal: We will explore, study, prepare, and successfully perform piano literature composed for one piano-four hands (duet), one piano-six hands (trio), two pianos-four hands (duo), and two pianos-eight hands (quartet). This course is designed to improve piano sight-reading skills, enhance musicianship, improve interpretive skills, and review good performance practice for piano music. The culmination of the semester is a performance in Beckwith Recital Hall on Sunday, April 14, 2013 at 7:30. Attendance policy: Attendance is required! Be on time at the beginning of each rehearsal and stay until the end. The success of the ensemble depends on quality practice time and efficient, effective rehearsal techniques by all members. Except in emergencies, absences will not be excused. Exceptions may be made in the case of contagious or extended illness, but only if you have notified me in advance of the absence. If you have to miss and wish to be excused, use the phone number listed above. Please leave a voice message explaining the reason for your absence. If you share music, deliver the score for your partner before rehearsal. If you have to miss class, you are responsible for asking for and practicing assignments you may have missed. -

6Th Grade Music: String Quartets
Name: ______________________________________ Music 6___________ 6th Grade Music: String Quartets Instructions: Read the information below (this came from the website https://www.liveabout.com/string-quartet-101-723913). Prompt #1: Answer these questions using complete sentences. 1. Use your own words to describe what a string quartet is. 2. String quartets are usually made up of four movements (sections). Which of the four movements are usually fast? Circle all that apply a. First movement b. Second movement c. Third movement d. Fourth movement. Prompt #2: Under “Notable String Quartet Composers” below, choose one YouTube video to listen to. You do not need to listen to the entire video. Answer the following questions as you watch and listen: 1. Write the name of the composer you chose. 2. Is the beginning slow (Adagio) or fast (Allegro)? 3. The musicians are seated in a certain order. How do their instruments relate to that order? Information was found on this website: https://www.liveabout.com/string-quartet-101-723913 4. How do the musicians respond to each other while playing? Prompt #3: Under Modern String Quartet Music, find the Love Story quartet by Taylor Swift. Listen to it as you answer using complete sentences. 1. Which instrument is plucking at the beginning of the piece? (If you forgot, violins are the smallest instrument, violas are a little bigger, cellos are bigger and lean on the floor). 2. Reflect on how this version of Love Story is different from Taylor Swift’s original song. How would you describe the differences? What does this version communicate? Information was found on this website: https://www.liveabout.com/string-quartet-101-723913 String Quartet 101 All You Need to Know About the String Quartet The Jerusalem Quartet, a string quartet made of members (from left) Alexander Pavlovsky, Sergei Bresler, Kyril Zlontnikov and Ori Kam, perform Brahms’s String Quartet in A minor at the 92nd Street Y on Saturday night, October 25, 2014.