DOCSLIB.ORG

The Circle Constant Remastered for Less Misconceptions

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
The Circle Constant Remastered for Less Misconceptions The circle constant remastered for less misconceptions A textual analysis of the introduction of radians in mathematics education textbooks for the Swedish upper secondary school Jesper Lindkvist Department of Mathematics and Science Education Degree Project in Science Education in Postgraduate programme in Education (PGCE), UM9100, 15 HE credits Mathematics Education Bridging Teacher Education Programme in Mathematics, Science and Technology for Graduates with a Third Cycle Degree, 90 HE credits Autumn term 2019 Supervisor: Professor Paola Valero Examiner: Docent Per Sund The circle constant remastered for less misconceptions A textual analysis of the introduction of radians in mathematics education textbooks for the Swedish upper secondary school Jesper Lindkvist Abstract The circle constant, the number pi (p ≈ 3:14), is defined as the ratio between the circumference of a circle to its diameter. When it comes to radians, the angle measurement which relates the circumference of a circle to its radius, one turn equals two pi. This extra constant of two is something everyone has to remember and practice. An extra constant of two shows up in several equations in both mathematics and physics, which still are mathematically correct, but is there due to our way of defining the circle constant. Researchers have therefore recently suggested a new circle constant, tau (t ≈ 6:28), which instead equals two pi. Now one turn equals one tau, and equations become more generalised, simpler and more aesthetic, some people argue. This means that pi could potentially be the cause of misconceptions when pupils learn the concept of radians in upper secondary schools, and should be investigated further in a school setting. A first exploration of problems related to the introduction of radians is thus needed. In this study, I define the problem of using pi from three perspectives: aesthetics, mathematics, and usefulness in both mathematics and physics. A textual analysis of the introduction of radians in the textbooks used for the upper secondary school mathematics is the main topic of the study. A proposed alternative way where tau is used instead of pi is given as a constructed textbook example. The analysis of the sections introducing radians of mathematics textbooks for the Swedish upper secondary school shows that pi is often introduced by first stating that one full circle corresponds to 360◦ = 2p, and then always adding the extra comment that half a turn is equal to pi, i.e. 180◦ = p. This results in pupils having to remember an exception to a rule. Radians are always implemented in the textbooks in order to work with circle arc lengths and circle segment areas. When pi is used, these equations differ from the looks of the equations for the circle circumference and the circle area with a factor two. In a constructed textbook example that introduces radians, I use tau instead of pi, and the above problems are averted. This study shows that tau is both aesthetically pleasing and practically useful in some parts of mathematics and physics. Using tau instead of pi could make misconceptions less likely to happen, which is exactly why this field and topic need to be researched more in a classroom setting with pupils. Keywords tau, pi, radians, misconceptions, circle constant, pedagogical disaster, mathematics education Contents Contents . i Introduction . 1 Motivation . 1 Short history of pi . 2 Background of tau . 2 Pi or tau: a pedagogical disaster? . 6 Long term aims and research questions . 7 Method . 8 Analysis and results . 9 Why radians are introduced . 9 How pi and radians are introduced . 10 Using radians . 11 Summary . 11 Discussion and conclusion . 12 Bibliography . 15 Appendix: A constructed textbook example on how to introduce radians with tau . 17 i Introduction Motivation Perhaps the most interesting part of every research project is the motivation that fuels it. Ever since I was a young student myself, the concept of the number pi, p ≈ 3:14, always felt like a needle in my eye. This study explores the concept of an alternative constant, which instead equals two pi. It has previously been suggested by the theoretical physicist dr Michael Hartl, University of California, that this alternative constant should be named tau, t ≈ 6:28 (Hartl, 2010). When I was in the Swedish upper secondary school myself in the years 2002–2005, I remember when the mathematics teacher introduced us to radians (in the Matematik D course). Mathematical beauty and simplicity has always awed me, but now I instead felt a sense of dissonance with regards to pi and radians. The radian concept was not hard for me to grasp, and I realised the beauty of radians immediately, but not its combination with pi. My first instincts were that two pi was a better constant, but as I spent time philosophising about the new concepts I just learned, it was not to dismiss pi, but rather to find ways to make pi seem more special. I came to the conclusion that the period of zeroes in the sine, cosine, and tangent functions is for instance equal to pi, so my mind was satisfied for that moment. When we in the next course (Matematik E) got into contact with Euler’s formula, eix = cosx + isinx; (1) I realised that the fundamental circle constant should not be described with pi, but rather two pi, due to two pi being the rotation that mapped back to the same number in the complex plane. After having had a mental struggle for half a year, I had at least sorted things out for myself. My ambition is that no person should ever even have to face this struggle and the possible misconceptions that arise from it. Why would they have to? Mathematics should be simple, beautiful, logical, and useful. To be able to advance in our knowledge-based society, we shouldn’t be afraid to admit and change our past mistakes. As an active researcher in physics, the number two pi pops up frequently in my equations. The most common examples are the Gaussian (normal) distribution and the Fourier transform. Since I am developing my own simulation codes (Lindkvist, 2018), I have to optimise the programming in such a way to minimise calculations, but also make the code readable. Achieving both of these goals is usually done by defining a constant called something along the lines of “twopi”. People reading the code will understand its meaning, while the computer can be efficient at the same time. The unnecessary operation of multiplying with two is often not the bottleneck for optimisation of a physical simulation code, but it is still something one wants to avoid if the multiplication is done in a nested for-loop. If the same multiplication with two is done several billion times over and over again, it will cut down the running time of the program. When it comes to memory storage, two pi and pi both take the same amount of memory when stored as the same floating point data type, but they also have the same amount of precision. The reason is that a floating point number is stored in bits, either 32 (single precision) or 64 (double precision) in the IEEE 754 standard for floating-point arithmetic (IEEE Standards Association, 2019). Taking the 32 bit example, a floating point number has 1 bit deciding the sign of the number, 8 bits deciding the exponent to multiply with, and 23 bits as the mantissa, or significand (the digits after the leading one of a number in binary). Tau would for instance be stored in memory as 0 10000001 10010010000111111011011 (2) and if each of these sections are seen as binary numbers, it results in representing the floating point number 1 as t = 2p ≈ (−1)(signedbit) · 2(exponentbitsminus127) · 1:(significandbits) = (−1)0 · 2(129−127) · 1:570796251296997 (3) = 6:283185005187988 The programming language Python is one of many programming languages that has implemented tau into their numeric and mathematical modules since release 3.6 (Python Software Foundation, 2019). Tau is stored as the constant “math.tau” with the following documentation: The mathematical constant t = 6:283185:::, to available precision. Tau is a circle constant equal to 2p, the ratio of a circle’s circumference to its radius. To learn more about Tau, check out Vi Hart’s video Pi is (still) Wrong, and start celebrating Tau day by eating twice as much pie! This is a result of tau becoming more popular in the scientific community. At least one paper in the field of mathematical analysis has been published using tau instead of pi (Harremoës, 2016). Short history of pi One cannot argue that pi has great historical importance. The first way of representing the circle constant in a rigorous algorithm using polygons started with Archimedes in ancient Greece around 240 BCE (Berggren et al., 1997). It wasn’t until the mathematician William Jones used the notation for pi for the ratio between half the periphery and the radius (or the periphery and the diameter) of a circle in 1706 (Berggren et al., 1997). Pi had been used to denote the periphery of a circle with any radius before, but it was the renowned mathematician Leonard Euler who later popularized the use of pi we know today, i.e. as the ratio between the periphery and the diameter of a circle (Berggren et al., 1997). From a practical point of view, I can imagine that it is easier to measure the diameter of a circle than its radius. Background of tau The number pi is defined as the ratio between the circumference of a circle to its diameter. Unfortunately, the diameter is not the defining property of a circle.
Load more

Recommended publications
  • The Enigmatic Number E: a History in Verse and Its Uses in the Mathematics Classroom
    To appear in MAA Loci: Convergence The Enigmatic Number e: A History in Verse and Its Uses in the Mathematics Classroom Sarah Glaz Department of Mathematics University of Connecticut Storrs, CT 06269 [email protected] Introduction In this article we present a history of e in verse—an annotated poem: The Enigmatic Number e . The annotation consists of hyperlinks leading to biographies of the mathematicians appearing in the poem, and to explanations of the mathematical notions and ideas presented in the poem. The intention is to celebrate the history of this venerable number in verse, and to put the mathematical ideas connected with it in historical and artistic context. The poem may also be used by educators in any mathematics course in which the number e appears, and those are as varied as e's multifaceted history. The sections following the poem provide suggestions and resources for the use of the poem as a pedagogical tool in a variety of mathematics courses. They also place these suggestions in the context of other efforts made by educators in this direction by briefly outlining the uses of historical mathematical poems for teaching mathematics at high-school and college level. Historical Background The number e is a newcomer to the mathematical pantheon of numbers denoted by letters: it made several indirect appearances in the 17 th and 18 th centuries, and acquired its letter designation only in 1731. Our history of e starts with John Napier (1550-1617) who defined logarithms through a process called dynamical analogy [1]. Napier aimed to simplify multiplication (and in the same time also simplify division and exponentiation), by finding a model which transforms multiplication into addition.
    [Show full text]
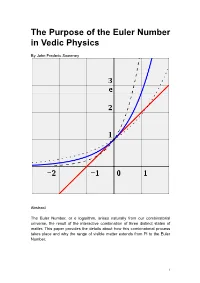
  • Euler Number in Vedic Physics
    The Purpose of the Euler Number in Vedic Physics By John Frederic Sweeney Abstract The Euler Number, or e logarithm, arises naturally from our combinatorial universe, the result of the interactive combination of three distinct states of matter. This paper provides the details about how this combinatorial process takes place and why the range of visible matter extends from Pi to the Euler Number. 1 Table of Contents Introduction 3 Wikipedia on the Euler Number 5 Vedic Physics on the Euler Number 6 Conclusion 8 Bibliography 9 2 Introduction The author posted a few papers on Vixra during 2013 which made statements about Pi and the Euler Number that lacked support. This paper offers the support for those statements. Since the explanation is mired, twisted and difficult to follow, the author wished to make other aspects of Vedic Particle Physics clear. This paper begins with Wikipedia on Euler, then to the Vedic Explanation. This paper, along with Why Pi? Which explains the reason why Pi carries such importance in a combinatorial world, should make it easier for readers to grasp the fundamental concepts of Vedic Particle Physics. Essentially, three states of matter exist in a combinatorial world, the axes of the states run from Pi to the Euler number. The simple formula of n + 1 suggests Pascal’s Triangle or Mount Meru, and the author has published a paper on this theme about Clifford Algebras, suggesting them as a most useful tool in a combinatorial universe. Someone once said that only those with clear understanding can explain things clearly and simply to others.
    [Show full text]
  • Multidisciplinary Design Project Engineering Dictionary Version 0.0.2
    Multidisciplinary Design Project Engineering Dictionary Version 0.0.2 February 15, 2006 . DRAFT Cambridge-MIT Institute Multidisciplinary Design Project This Dictionary/Glossary of Engineering terms has been compiled to compliment the work developed as part of the Multi-disciplinary Design Project (MDP), which is a programme to develop teaching material and kits to aid the running of mechtronics projects in Universities and Schools. The project is being carried out with support from the Cambridge-MIT Institute undergraduate teaching programe. For more information about the project please visit the MDP website at http://www-mdp.eng.cam.ac.uk or contact Dr. Peter Long Prof. Alex Slocum Cambridge University Engineering Department Massachusetts Institute of Technology Trumpington Street, 77 Massachusetts Ave. Cambridge. Cambridge MA 02139-4307 CB2 1PZ. USA e-mail: [email protected] e-mail: [email protected] tel: +44 (0) 1223 332779 tel: +1 617 253 0012 For information about the CMI initiative please see Cambridge-MIT Institute website :- http://www.cambridge-mit.org CMI CMI, University of Cambridge Massachusetts Institute of Technology 10 Miller’s Yard, 77 Massachusetts Ave. Mill Lane, Cambridge MA 02139-4307 Cambridge. CB2 1RQ. USA tel: +44 (0) 1223 327207 tel. +1 617 253 7732 fax: +44 (0) 1223 765891 fax. +1 617 258 8539 . DRAFT 2 CMI-MDP Programme 1 Introduction This dictionary/glossary has not been developed as a definative work but as a useful reference book for engi- neering students to search when looking for the meaning of a word/phrase. It has been compiled from a number of existing glossaries together with a number of local additions.
    [Show full text]
  • The Exponential Constant E
    The exponential constant e mc-bus-expconstant-2009-1 Introduction The letter e is used in many mathematical calculations to stand for a particular number known as the exponential constant. This leaflet provides information about this important constant, and the related exponential function. The exponential constant The exponential constant is an important mathematical constant and is given the symbol e. Its value is approximately 2.718. It has been found that this value occurs so frequently when mathematics is used to model physical and economic phenomena that it is convenient to write simply e. It is often necessary to work out powers of this constant, such as e2, e3 and so on. Your scientific calculator will be programmed to do this already. You should check that you can use your calculator to do this. Look for a button marked ex, and check that e2 =7.389, and e3 = 20.086 In both cases we have quoted the answer to three decimal places although your calculator will give a more accurate answer than this. You should also check that you can evaluate negative and fractional powers of e such as e1/2 =1.649 and e−2 =0.135 The exponential function If we write y = ex we can calculate the value of y as we vary x. Values obtained in this way can be placed in a table. For example: x −3 −2 −1 01 2 3 y = ex 0.050 0.135 0.368 1 2.718 7.389 20.086 This is a table of values of the exponential function ex.
    [Show full text]
  • Two Worked out Examples of Rotations Using Quaternions
    TWO WORKED OUT EXAMPLES OF ROTATIONS USING QUATERNIONS This note is an attachment to the article \Rotations and Quaternions" which in turn is a companion to the video of the talk by the same title. Example 1. Determine the image of the point (1; −1; 2) under the rotation by an angle of 60◦ about an axis in the yz-plane that is inclined at an angle of 60◦ to the positive y-axis. p ◦ ◦ 1 3 Solution: The unit vector u in the direction of the axis of rotation is cos 60 j + sin 60 k = 2 j + 2 k. The quaternion (or vector) corresponding to the point p = (1; −1; 2) is of course p = i − j + 2k. To find −1 θ θ the image of p under the rotation, we calculate qpq where q is the quaternion cos 2 + sin 2 u and θ the angle of rotation (60◦ in this case). The resulting quaternion|if we did the calculation right|would have no constant term and therefore we can interpret it as a vector. That vector gives us the answer. p p p p p We have q = 3 + 1 u = 3 + 1 j + 3 k = 1 (2 3 + j + 3k). Since q is by construction a unit quaternion, 2 2 2 4 p4 4 p −1 1 its inverse is its conjugate: q = 4 (2 3 − j − 3k). Now, computing qp in the routine way, we get 1 p p p p qp = ((1 − 2 3) + (2 + 3 3)i − 3j + (4 3 − 1)k) 4 and then another long but routine computation gives 1 p p p qpq−1 = ((10 + 4 3)i + (1 + 2 3)j + (14 − 3 3)k) 8 The point corresponding to the vector on the right hand side in the above equation is the image of (1; −1; 2) under the given rotation.
    [Show full text]
  • Circular Motion and Newton's Law of Gravitation
    CIRCULAR MOTION AND NEWTON’S LAW OF GRAVITATION I. Speed and Velocity Speed is distance divided by time…is it any different for an object moving around a circle? The distance around a circle is C = 2πr, where r is the radius of the circle So average speed must be the circumference divided by the time to get around the circle once C 2πr one trip around the circle is v = = known as the period. We’ll use T T big T to represent this time SINCE THE SPEED INCREASES WITH RADIUS, CAN YOU VISUALIZE THAT IF YOU WERE SITTING ON A SPINNING DISK, YOU WOULD SPEED UP IF YOU MOVED CLOSER TO THE OUTER EDGE OF THE DISK? 1 These four dots each make one revolution around the disk in the same time, but the one on the edge goes the longest distance. It must be moving with a greater speed. Remember velocity is a vector. The direction of velocity in circular motion is on a tangent to the circle. The direction of the vector is ALWAYS changing in circular motion. 2 II. ACCELERATION If the velocity vector is always changing EQUATIONS: in circular motion, THEN AN OBJECT IN CIRCULAR acceleration in circular MOTION IS ACCELERATING. motion can be written as, THE ACCELERATION VECTOR POINTS v2 INWARD TO THE CENTER OF THE a = MOTION. r Pick two v points on the path. 2 Subtract head to tail…the 4π r v resultant is the change in v or a = 2 f T the acceleration vector vi a a Assignment: check the units -vi and do the algebra to make vf sure you believe these equations Note that the acceleration vector points in 3 III.
    [Show full text]
  • Trigonometric Functions
    72 Chapter 4 Trigonometric Functions To define the radian measurement system, we consider the unit circle in the xy-plane: ........................ ....... ....... ...... ....................... .............. ............... ......... ......... ....... ....... ....... ...... ...... ...... ..... ..... ..... ..... ..... ..... .... ..... ..... .... .... .... .... ... (cos x, sin x) ... ... 4 ... A ..... .. ... ....... ... ... ....... ... .. ....... .. .. ....... .. .. ....... .. .. ....... .. .. ....... .. .. ....... ...... ....... ....... ...... ....... x . ....... Trigonometric Functions . ...... ....y . ....... (1, 0) . ....... ....... .. ...... .. .. ....... .. .. ....... .. .. ....... .. .. ....... .. ... ...... ... ... ....... ... ... .......... ... ... ... ... .... B... .... .... ..... ..... ..... ..... ..... ..... ..... ..... ...... ...... ...... ...... ....... ....... ........ ........ .......... .......... ................................................................................... An angle, x, at the center of the circle is associated with an arc of the circle which is said to subtend the angle. In the figure, this arc is the portion of the circle from point (1, 0) So far we have used only algebraic functions as examples when finding derivatives, that is, to point A. The length of this arc is the radian measure of the angle x; the fact that the functions that can be built up by the usual algebraic operations of addition, subtraction, radian measure is an actual geometric length is largely responsible for the usefulness of
    [Show full text]
  • Crystals of Golden Proportions
    THE NOBEL PRIZE IN CHEMISTRY 2011 INFORMATION FOR THE PUBLIC Crystals of golden proportions When Dan Shechtman entered the discovery awarded with the Nobel Prize in Chemistry 2011 into his notebook, he jotted down three question marks next to it. The atoms in the crystal in front of him yielded a forbidden symmetry. It was just as impossible as a football – a sphere – made of only six- cornered polygons. Since then, mosaics with intriguing patterns and the golden ratio in mathematics and art have helped scientists to explain Shechtman’s bewildering observation. “Eyn chaya kazo”, Dan Shechtman said to himself. “There can be no such creature” in Hebrew. It was the morning of 8 April 1982. The material he was studying, a mix of aluminum and manganese, was strange- looking, and he had turned to the electron microscope in order to observe it at the atomic level. However, the picture that the microscope produced was counter to all logic: he saw concentric circles, each made of ten bright dots at the same distance from each other (fgure 1). Shechtman had rapidly chilled the glowing molten metal, and the sudden change in temperature should have created complete disorder among the atoms. But the pattern he observed told a completely different story: the atoms were arranged in a manner that was contrary to the laws of nature. Shechtman counted and recounted the dots. Four or six dots in the circles would have been possible, but absolutely not ten. He made a notation in his notebook: 10 Fold??? BRIGHT DOTS will DARKNESS results appear where wave where crests and crests intersect and troughs meet and reinforce each other.
    [Show full text]
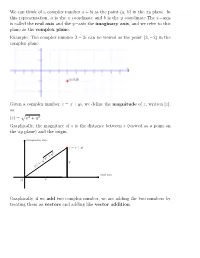
  • We Can Think of a Complex Number a + Bi As the Point (A, B) in the Xy Plane
    We can think of a complex number a + bi as the point (a, b) in the xy plane. In this representation, a is the x coordinate and b is the y coordinate.The x−axis is called the real axis and the y−axis the imaginary axis, and we refer to this plane as the complex plane. Example: The complex number 3 − 2i can be viewed as the point (3; −2) in the complex plane. Given a complex number z = x + yi, we define the magnitude of z, written jzj, as: jzj = px2 + y2. Graphically, the magniture of z is the distance between z (viewed as a point on the xy plane) and the origin. imaginary axis z = x + yi 2 y 2 + x p y j = jz real axis O x Graphically, if we add two complex number, we are adding the two numbers by treating them as vectors and adding like vector addition. For example, Let z = 5 + 2i, w = 1 + 6i, then z + w = (5 + 2i) + (1 + 6i) = (5 + 1) + (2 + 6)i = 6 + 8i In order to interpret multiplication of two complex numbers, let's look again at the complex number represented as a point on the complex plane. This time, we let r = px2 + y2 be the magnitude of z. Let 0 ≤ θ < 2π be the angle in standard position with z being its terminal point. We call θ the argument of the complex number z: imaginary axis imaginary axis z = x + yi z = x + yi 2 y 2 + p x r j = y y jz = r θ real axis θ real axis O x O x By definition of sine and cosine, we have x cos(θ) = ) x = r cos(θ) r y sin(θ) = ) y = r sin(θ) r We have obtained the polar representation of a complex number: Suppose z = x + yi is a complex number with (x; y) in rectangular coordinate.
    [Show full text]
  • List of Mathematical Symbols by Subject from Wikipedia, the Free Encyclopedia
    List of mathematical symbols by subject From Wikipedia, the free encyclopedia This list of mathematical symbols by subject shows a selection of the most common symbols that are used in modern mathematical notation within formulas, grouped by mathematical topic. As it is virtually impossible to list all the symbols ever used in mathematics, only those symbols which occur often in mathematics or mathematics education are included. Many of the characters are standardized, for example in DIN 1302 General mathematical symbols or DIN EN ISO 80000-2 Quantities and units – Part 2: Mathematical signs for science and technology. The following list is largely limited to non-alphanumeric characters. It is divided by areas of mathematics and grouped within sub-regions. Some symbols have a different meaning depending on the context and appear accordingly several times in the list. Further information on the symbols and their meaning can be found in the respective linked articles. Contents 1 Guide 2 Set theory 2.1 Definition symbols 2.2 Set construction 2.3 Set operations 2.4 Set relations 2.5 Number sets 2.6 Cardinality 3 Arithmetic 3.1 Arithmetic operators 3.2 Equality signs 3.3 Comparison 3.4 Divisibility 3.5 Intervals 3.6 Elementary functions 3.7 Complex numbers 3.8 Mathematical constants 4 Calculus 4.1 Sequences and series 4.2 Functions 4.3 Limits 4.4 Asymptotic behaviour 4.5 Differential calculus 4.6 Integral calculus 4.7 Vector calculus 4.8 Topology 4.9 Functional analysis 5 Linear algebra and geometry 5.1 Elementary geometry 5.2 Vectors and matrices 5.3 Vector calculus 5.4 Matrix calculus 5.5 Vector spaces 6 Algebra 6.1 Relations 6.2 Group theory 6.3 Field theory 6.4 Ring theory 7 Combinatorics 8 Stochastics 8.1 Probability theory 8.2 Statistics 9 Logic 9.1 Operators 9.2 Quantifiers 9.3 Deduction symbols 10 See also 11 References 12 External links Guide The following information is provided for each mathematical symbol: Symbol: The symbol as it is represented by LaTeX.
    [Show full text]
  • Chapter 4: Circular Motion
    Chapter 4: Circular Motion ! Why do pilots sometimes black out while pulling out at the bottom of a power dive? ! Are astronauts really "weightless" while in orbit? ! Why do you tend to slide across the car seat when the car makes a sharp turn? Make sure you know how to: 1. Find the direction of acceleration using the motion diagram. 2. Draw a force diagram. 3. Use a force diagram to help apply Newton’s second law in component form. CO: Ms. Kruti Patel, a civilian test pilot, wears a special flight suit and practices special breathing techniques to prevent dizziness, disorientation, and possibly passing out as she pulls out of a power dive. This dizziness, or worse, is called a blackout and occurs when there is a lack of blood to the head and brain. Tony Wayne in his book Ride Physiology describes the symptoms of blackout. As the acceleration climbs up toward 7 g , “you … can no longer see color. … An instant later, … your field of vision is shrinking. It now looks like you are seeing things through a pipe. … The visual pipe's diameter is getting smaller and smaller. In a flash you see black. You have just "blacked out." You are unconscious …” Why does blackout occur and why does a special suit prevent blackout? Our study of circular motion in this chapter will help us understand this and other interesting phenomena. Lead In the previous chapters we studied the motion of objects when the sum of the forces exerted on them was constant in terms of magnitude and direction.
    [Show full text]
  • Transcendence of Generalized Euler Constants Author(S): M
    Transcendence of Generalized Euler Constants Author(s): M. Ram Murty, Anastasia Zaytseva Source: The American Mathematical Monthly, Vol. 120, No. 1 (January 2013), pp. 48-54 Published by: Mathematical Association of America Stable URL: http://www.jstor.org/stable/10.4169/amer.math.monthly.120.01.048 . Accessed: 27/11/2013 11:47 Your use of the JSTOR archive indicates your acceptance of the Terms & Conditions of Use, available at . http://www.jstor.org/page/info/about/policies/terms.jsp . JSTOR is a not-for-profit service that helps scholars, researchers, and students discover, use, and build upon a wide range of content in a trusted digital archive. We use information technology and tools to increase productivity and facilitate new forms of scholarship. For more information about JSTOR, please contact [email protected]. Mathematical Association of America is collaborating with JSTOR to digitize, preserve and extend access to The American Mathematical Monthly. http://www.jstor.org This content downloaded from 14.139.163.28 on Wed, 27 Nov 2013 11:47:04 AM All use subject to JSTOR Terms and Conditions Transcendence of Generalized Euler Constants M. Ram Murty and Anastasia Zaytseva Abstract. We consider a class of analogues of Euler’s constant γ and use Baker’s theory of linear forms in logarithms to study its arithmetic properties. In particular, we show that with at most one exception, all of these analogues are transcendental. 1. INTRODUCTION. There are two types of numbers: algebraic and transcenden- tal. A complex number is called algebraic if it is a root of some algebraic equation with integer coefficients.
    [Show full text]