DOCSLIB.ORG

Artificial Neural Networks· T\ Briet In!Toquclion

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Artificial Neural Networks· T\ Briet In!Toquclion GENERAL I ARTICLE Artificial Neural Networks· t\ BrieT In!TOQuclion Jitendra R Raol and Sunilkumar S Mankame Artificial neural networks are 'biologically' inspired net­ works. They have the ability to learn from empirical datal information. They find use in computer science and control engineering fields. In recent years artificial neural networks (ANNs) have fascinated scientists and engineers all over the world. They have the ability J R Raol is a scientist with to learn and recall - the main functions of the (human) brain. A NAL. His research major reason for this fascination is that ANNs are 'biologically' interests are parameter inspired. They have the apparent ability to imitate the brain's estimation, neural networks, fuzzy systems, activity to make decisions and draw conclusions when presented genetic algorithms and with complex and noisy information. However there are vast their applications to differences between biological neural networks (BNNs) of the aerospace problems. He brain and ANN s. writes poems in English. A thorough understanding of biologically derived NNs requires knowledge from other sciences: biology, mathematics and artifi­ cial intelligence. However to understand the basics of ANNs, a knowledge of neurobiology is not necessary. Yet, it is a good idea to understand how ANNs have been derived from real biological neural systems (see Figures 1,2 and the accompanying boxes). The soma of the cell body receives inputs from other neurons via Sunilkumar S Mankame is adaptive synaptic connections to the dendrites and when a neuron a graduate research student from Regional is excited, the nerve impulses from the soma are transmitted along Engineering College, an axon to the synapses of other neurons. The artificial neurons Calicut working on direct are called neuron cells, processing elements or nodes. They neural network based attempt to simulate the structure and function of biological (real) adaptive control. neurons. Artificial neural models are loosely based on biology since a complete understanding of the behaviour of real neuronal systems is lacking. The point is that only a part of the behaviour of real neurons is necessary for their information capacity. Also, ---------------- ---- RESONANCE ·I February. 1996 47 GENERAL ! ARTICLE input signals ~ndritiC spine l where synapse n ~+axons ~ is possible p -----~ f t u ____-.J/ S P soma t summation u synapses soma threshold t (weights) Model of Artificial Neuron Figure 1 Biological and ar­ flflclal neuron models have Biological Neuron System certain features in common. Weights in ANN modeVrep­ • Dendrites input branching tree of fibres - connect to a set of other resent synapses of BNN. neurons-receptive surfaces for input signals • Soma cell body -all the logical functions ofthe neurons are realised here • Synapse specialized contacts on a neuron - interfaces some axons to the spines of the input dendrites - can increase/dampen the neuron excitation • Axon nerve fibre - final output channel - signals converted into nerve pulses (spikes) to target cells Artificial Neuron System • Input layer the layer of nodes for data entering on ANN • Hidden layer the layer between input and output layers • Output layer the layer of nodes that produce the network's output Artjfjcial neural responses networks have the • Weights strength or the (gain) value of the connection between appamnt obility to nodes imitate the brain's activity to make it is easier to implement/simulate simplified models rather than decisions and draw complex ones. conclusions when presented with The first model of an elementary neuron was outlined by complex and noisy McCulloch and Pitts in 1943. Their model included the elements information. needed to perform necessary computations, but they could not \..-~-------------.-- --- 48 RESONANCE I February 1996 GENERAL I ARTICLE --------- SignallInfonnation ------> flow output bias inputs input layer I hidden layer I output layer Feed Forward Neural Network Non-linear activation' f ' realise the model using the bulky vacuum tubes of that era. FIguf'fI2 A fyplCtlI arllfldtll McCulloch and Pitts must nevertheless be regarded as the pio­ neural network /fHd for­ neers in the field of neural networks. ward} does nofusIHII/y have fHdbtlck - fltIW of slglJQV Information Is Dnly In the ANNs are designed to realise very specific computational tasks/ folWtlrd dll'fldlon. A multi­ problems. They are highly interconnected, parallel computa­ layer fHd foIward neural tional structures with many relatively simple individual process­ nlltwork /FFNN} Is shown ing elements (Figure 2). A biological neuron either excites or here. The non-linear char­ inhibits all neurons to which it is connected, whereas in ANNs acterIsNcs of ANNs aM dUll to thll non-linear adMlflDn either excitatory or inhibitory neural connections are possible. fundlon f. This Is USBfuI for There are many kinds of neurons in BNNs, whereas in ANNs only accurate mtHllllllng ofnon­ certain types are used. It is possible to implement and study linear sysffIms.. various ANN architectures using simulations on a personal com­ puter (PC). Characteristics of non-linear systems Types of ANN s In non-linear systems, the output variables do not There are mainly two types of ANNs: feed forward neural net­ depend on the input vari­ works (FFNNs) and recurrent neural networks (RNN s). In FFNN ables in a linear manner. there are no feedback loops. The flow of signals/information is The dynamic characteris­ only in the forward direction. The behaviour of FFNN does not tics of the system itself depend on past input. The network responds only to its present would depend on either input. In RNN there are feedback loops (essent~ally FFNN with one or more of the follow­ output fed back to input). Different types of neural network ing: amplitude of the input architectures are briefly described next. signal. its wave form. its frequency. This is not so in • Single-layer feed forward networks: It has only one layer of the case of a linear system . 49 GENERAL I ARTICLE Figure 3 Recun-ent neural network has feedback loops unit with output fed back to in­ delay put. computational nodes. It is a feed forward network since it does not have any feedback. • Multi-layer feed forward networks: It is a feed forward network with one or more hidden layers. The source nodes in the input layer supply inputs to the neurons of the first hidden layer. The outputs of the first hidden layer neurons are applied as inputs to the neurons of the second hidden layer and so on (Figure 2). If The first model of an every node in each layer of the network is connected to every other elementary neuron node in the adjacent forward layer, then the network is called fully was outlined by connected. If however some of the links are missing, the network McCulloch and Pitts is said to be partially connected. Recall is instantaneous in this in 1943. The model type of network (we will discuss this later in the section on the included the uses of ANNs). These networks can be used to realise complex elements to perform input/output mappings. necessary computations , but • Recurrent neural networks: A recurrent neural network is one in they could not which there is at least one feedback loop. There are different kinds realisE ~ the model of recurrent networks depending on the way in which the feed­ using the bulky back is used. In a typical case it has a single layer of neurons with vacuum tubes of each neuron feeding its output signal back to the inputs of all that era. McCulloch other neurons. Other kinds of recurrent networks may have self­ and Pitts must feedback loops and also hidden neurons (Figure 3). nevertheless be rega rded as the • Lattice networks: A lattice network is a feed forward network pioneer s in the with the output neurons arranged in rows and columns. It can fie id of neural have one-dimensional, two-dimensional or higher dimensional netWorks. arrays of neurons with a corresponding set of source nodes that --------------------------------~-=~----------------------------- 50 RESONANCE I February 1996 GENERAL ! ARTICLE Input_yer of source :rerinput nodes source nodes One Dimensional Two-Dimensional supply the input signals to the array. A one-dimensional network Figure 4 tafflce networks of three neurons fed from a layer of three source nodes and a two­ are FFNNs with output neu­ rons a"anged In rows and dimensional lattice of 2-by-2 neurons fed from a layer of two columns. The one-dimen­ source nodes are shown in Figure 4. Each source node is connected sional nefwDrk offhree neu­ to every neuron in the lattice network. rons shown here Is fed from a layer of three source There are also other types of ANNs: Kohonen nets, adaptive nodes. The fwD-dimensional resonance theory (ART) network, radial basis function (RBF) lafflce Is fed from a layer of network, etc., which we will not consider now. two source nodes. Training an ANN A learning scheme for updating a neuron's connections (weights) was proposed by Donald Hebb in 1949. A new powerful learning law called the Widrow-H offleaming rule was developed by Bernard Widrow and Marcian Hoff in 1960. How does an ANN achieve 'what it achieves'? In general, an ANN structure is trained with known samples of data. As an example, if a particular pattern is to be recognised, then the ANN is first trained with the known pattern/information (in the form of digital signals). Then the ANN is ready to recognise a similar ANNs are used for pattern when it is presented to the network. If an ANN is trained pattern recognition, with a character 'H' , then it must be able to recognise this image processing, character when some noisy/fuzzy H is presented to it. A Japanese signal processing/ optical character recognition (OCR) system has an accuracy of prediction, adaptive about 99% in recognising characters from thirteen fonts used to control and other train the ANN.
Load more

Recommended publications
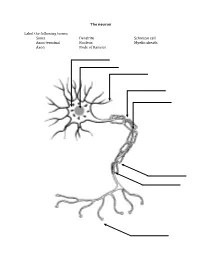
  • The Neuron Label the Following Terms: Soma Axon Terminal Axon Dendrite
    The neuron Label the following terms: Soma Dendrite Schwaan cell Axon terminal Nucleus Myelin sheath Axon Node of Ranvier Neuron Vocabulary You must know the definitions of these terms 1. Synaptic Cleft 2. Neuron 3. Impulse 4. Sensory Neuron 5. Motor Neuron 6. Interneuron 7. Body (Soma) 8. Dendrite 9. Axon 10. Action Potential 11. Myelin Sheath (Myelin) 12. Afferent Neuron 13. Threshold 14. Neurotransmitter 15. Efferent Neurons 16. Axon Terminal 17. Stimulus 18. Refractory Period 19. Schwann 20. Nodes of Ranvier 21. Acetylcholine STEPS IN THE ACTION POTENTIAL 1. The presynaptic neuron sends neurotransmitters to postsynaptic neuron. 2. Neurotransmitters bind to receptors on the postsynaptic cell. - This action will either excite or inhibit the postsynaptic cell. - The soma becomes more positive. 3. The positive charge reaches the axon hillock. - Once the threshold of excitation is reached the neuron will fire an action potential. 4. Na+ channels open and Na+ is forced into the cell by the concentration gradient and the electrical gradient. - The neuron begins to depolarize. 5. The K+ channels open and K+ is forced out of the cell by the concentration gradient and the electrical gradient. - The neuron is depolarized. 6. The Na+ channels close at the peak of the action potential. - The neuron starts to repolarize. 7. The K+ channels close, but they close slowly and K+ leaks out. 8. The terminal buttons release neurotransmitter to the postsynaptic neuron. 9. The resting potential is overshot and the neuron falls to a -90mV (hyperpolarizes). - The neuron continues to repolarize. 10. The neuron returns to resting potential. The Synapse Label the following terms: Pre-synaptic membrane Neurotransmitters Post-synaptic membrane Synaptic cleft Vesicle Post-synaptic receptors .
    [Show full text]
  • Crayfish Escape Behavior and Central Synapses
    Crayfish Escape Behavior and Central Synapses. III. Electrical Junctions and Dendrite Spikes in Fast Flexor Motoneurons ROBERT S. ZUCKER Department of Biological Sciences and Program in the Neurological Sciences, Stanford University, Stanford, California 94305 THE LATERAL giant fiber is the decision fiber and fast flexor motoneurons are located in for a behavioral response in crayfish in- the dorsal neuropil of each abdominal gan- volving rapid tail flexion in response to glion. Dye injections and anatomical recon- abdominal tactile stimulation (27). Each structions of ‘identified motoneurons reveal lateral giant impulse is followed by a rapid that only those motoneurons which have tail flexion or tail flip, and when the giant dentritic branches in contact with a giant fiber does not fire in response to such stim- fiber are activated by that giant fiber (12, uli, the movement does not occur. 21). All of tl ie fast flexor motoneurons are The afferent limb of the reflex exciting excited by the ipsilateral giant; all but F4, the lateral giant has been described (28), F5 and F7 are also excited by the contra- and the habituation of the behavior has latkral giant (21 a). been explained in terms of the properties The excitation of these motoneurons, of this part of the neural circuit (29). seen as depolarizing potentials in their The properties of the neuromuscular somata, does not always reach threshold for junctions between the fast flexor motoneu- generating a spike which propagates out the rons and the phasic flexor muscles have also axon to the periphery (14). Indeed, only t,he been described (13).
    [Show full text]
  • Artificial Neural Networks Part 2/3 – Perceptron
    Artificial Neural Networks Part 2/3 – Perceptron Slides modified from Neural Network Design by Hagan, Demuth and Beale Berrin Yanikoglu Perceptron • A single artificial neuron that computes its weighted input and uses a threshold activation function. • It effectively separates the input space into two categories by the hyperplane: wTx + b = 0 Decision Boundary The weight vector is orthogonal to the decision boundary The weight vector points in the direction of the vector which should produce an output of 1 • so that the vectors with the positive output are on the right side of the decision boundary – if w pointed in the opposite direction, the dot products of all input vectors would have the opposite sign – would result in same classification but with opposite labels The bias determines the position of the boundary • solve for wTp+b = 0 using one point on the decision boundary to find b. Two-Input Case + a = hardlim(n) = [1 2]p + -2 w1, 1 = 1 w1, 2 = 2 - Decision Boundary: all points p for which wTp + b =0 If we have the weights and not the bias, we can take a point on the decision boundary, p=[2 0]T, and solving for [1 2]p + b = 0, we see that b=-2. p w wT.p = ||w||||p||Cosθ θ Decision Boundary proj. of p onto w proj. of p onto w T T w p + b = 0 w p = -bœb = ||p||Cosθ 1 1 = wT.p/||w|| • All points on the decision boundary have the same inner product (= -b) with the weight vector • Therefore they have the same projection onto the weight vector; so they must lie on a line orthogonal to the weight vector ADVANCED An Illustrative Example Boolean OR ⎧ 0 ⎫ ⎧ 0 ⎫ ⎧ 1 ⎫ ⎧ 1 ⎫ ⎨p1 = , t1 = 0 ⎬ ⎨p2 = , t2 = 1 ⎬ ⎨p3 = , t3 = 1⎬ ⎨p4 = , t4 = 1⎬ ⎩ 0 ⎭ ⎩ 1 ⎭ ⎩ 0 ⎭ ⎩ 1 ⎭ Given the above input-output pairs (p,t), can you find (manually) the weights of a perceptron to do the job? Boolean OR Solution 1) Pick an admissable decision boundary 2) Weight vector should be orthogonal to the decision boundary.
    [Show full text]
  • Plp-Positive Progenitor Cells Give Rise to Bergmann Glia in the Cerebellum
    Citation: Cell Death and Disease (2013) 4, e546; doi:10.1038/cddis.2013.74 OPEN & 2013 Macmillan Publishers Limited All rights reserved 2041-4889/13 www.nature.com/cddis Olig2/Plp-positive progenitor cells give rise to Bergmann glia in the cerebellum S-H Chung1, F Guo2, P Jiang1, DE Pleasure2,3 and W Deng*,1,3,4 NG2 (nerve/glial antigen2)-expressing cells represent the largest population of postnatal progenitors in the central nervous system and have been classified as oligodendroglial progenitor cells, but the fate and function of these cells remain incompletely characterized. Previous studies have focused on characterizing these progenitors in the postnatal and adult subventricular zone and on analyzing the cellular and physiological properties of these cells in white and gray matter regions in the forebrain. In the present study, we examine the types of neural progeny generated by NG2 progenitors in the cerebellum by employing genetic fate mapping techniques using inducible Cre–Lox systems in vivo with two different mouse lines, the Plp-Cre-ERT2/Rosa26-EYFP and Olig2-Cre-ERT2/Rosa26-EYFP double-transgenic mice. Our data indicate that Olig2/Plp-positive NG2 cells display multipotential properties, primarily give rise to oligodendroglia but, surprisingly, also generate Bergmann glia, which are specialized glial cells in the cerebellum. The NG2 þ cells also give rise to astrocytes, but not neurons. In addition, we show that glutamate signaling is involved in distinct NG2 þ cell-fate/differentiation pathways and plays a role in the normal development of Bergmann glia. We also show an increase of cerebellar oligodendroglial lineage cells in response to hypoxic–ischemic injury, but the ability of NG2 þ cells to give rise to Bergmann glia and astrocytes remains unchanged.
    [Show full text]
  • Neuregulin 1–Erbb2 Signaling Is Required for the Establishment of Radial Glia and Their Transformation Into Astrocytes in Cerebral Cortex
    Neuregulin 1–erbB2 signaling is required for the establishment of radial glia and their transformation into astrocytes in cerebral cortex Ralf S. Schmid*, Barbara McGrath*, Bridget E. Berechid†, Becky Boyles*, Mark Marchionni‡, Nenad Sˇ estan†, and Eva S. Anton*§ *University of North Carolina Neuroscience Center and Department of Cell and Molecular Physiology, University of North Carolina School of Medicine, Chapel Hill, NC 27599; †Department of Neurobiology, Yale University School of Medicine, New Haven, CT 06510; and ‡CeNes Pharamceuticals, Inc., Norwood, MA 02062 Communicated by Pasko Rakic, Yale University School of Medicine, New Haven, CT, January 27, 2003 (received for review December 12, 2002) Radial glial cells and astrocytes function to support the construction mine whether NRG-1-mediated signaling is involved in radial and maintenance, respectively, of the cerebral cortex. However, the glial cell development and differentiation in the cerebral cortex. mechanisms that determine how radial glial cells are established, We show that NRG-1 signaling, involving erbB2, may act in maintained, and transformed into astrocytes in the cerebral cortex are concert with Notch signaling to exert a critical influence in the not well understood. Here, we show that neuregulin-1 (NRG-1) exerts establishment, maintenance, and appropriate transformation of a critical role in the establishment of radial glial cells. Radial glial cell radial glial cells in cerebral cortex. generation is significantly impaired in NRG mutants, and this defect can be rescued by exogenous NRG-1. Down-regulation of expression Materials and Methods and activity of erbB2, a member of the NRG-1 receptor complex, leads Clonal Analysis to Study NRG’s Role in the Initial Establishment of to the transformation of radial glial cells into astrocytes.
    [Show full text]
  • Artificial Neuron Using Mos2/Graphene Threshold Switching Memristor
    University of Central Florida STARS Electronic Theses and Dissertations, 2004-2019 2018 Artificial Neuron using MoS2/Graphene Threshold Switching Memristor Hirokjyoti Kalita University of Central Florida Part of the Electrical and Electronics Commons Find similar works at: https://stars.library.ucf.edu/etd University of Central Florida Libraries http://library.ucf.edu This Masters Thesis (Open Access) is brought to you for free and open access by STARS. It has been accepted for inclusion in Electronic Theses and Dissertations, 2004-2019 by an authorized administrator of STARS. For more information, please contact [email protected]. STARS Citation Kalita, Hirokjyoti, "Artificial Neuron using MoS2/Graphene Threshold Switching Memristor" (2018). Electronic Theses and Dissertations, 2004-2019. 5988. https://stars.library.ucf.edu/etd/5988 ARTIFICIAL NEURON USING MoS2/GRAPHENE THRESHOLD SWITCHING MEMRISTOR by HIROKJYOTI KALITA B.Tech. SRM University, 2015 A thesis submitted in partial fulfilment of the requirements for the degree of Master of Science in the Department of Electrical and Computer Engineering in the College of Engineering and Computer Science at the University of Central Florida Orlando, Florida Summer Term 2018 Major Professor: Tania Roy © 2018 Hirokjyoti Kalita ii ABSTRACT With the ever-increasing demand for low power electronics, neuromorphic computing has garnered huge interest in recent times. Implementing neuromorphic computing in hardware will be a severe boost for applications involving complex processes such as pattern recognition. Artificial neurons form a critical part in neuromorphic circuits, and have been realized with complex complementary metal–oxide–semiconductor (CMOS) circuitry in the past. Recently, insulator-to-metal-transition (IMT) materials have been used to realize artificial neurons.
    [Show full text]
  • Neuron Morphology Influences Axon Initial Segment Plasticity
    Dartmouth College Dartmouth Digital Commons Dartmouth Scholarship Faculty Work 1-2016 Neuron Morphology Influences Axon Initial Segment Plasticity Allan T. Gulledge Dartmouth College, [email protected] Jaime J. Bravo Dartmouth College Follow this and additional works at: https://digitalcommons.dartmouth.edu/facoa Part of the Computational Neuroscience Commons, Molecular and Cellular Neuroscience Commons, and the Other Neuroscience and Neurobiology Commons Dartmouth Digital Commons Citation Gulledge, A.T. and Bravo, J.J. (2016) Neuron morphology influences axon initial segment plasticity, eNeuro doi:10.1523/ENEURO.0085-15.2016. This Article is brought to you for free and open access by the Faculty Work at Dartmouth Digital Commons. It has been accepted for inclusion in Dartmouth Scholarship by an authorized administrator of Dartmouth Digital Commons. For more information, please contact [email protected]. New Research Neuronal Excitability Neuron Morphology Influences Axon Initial Segment Plasticity1,2,3 Allan T. Gulledge1 and Jaime J. Bravo2 DOI:http://dx.doi.org/10.1523/ENEURO.0085-15.2016 1Department of Physiology and Neurobiology, Geisel School of Medicine at Dartmouth, Dartmouth-Hitchcock Medical Center, Lebanon, New Hampshire 03756, and 2Thayer School of Engineering at Dartmouth, Hanover, New Hampshire 03755 Visual Abstract In most vertebrate neurons, action potentials are initiated in the axon initial segment (AIS), a specialized region of the axon containing a high density of voltage-gated sodium and potassium channels. It has recently been proposed that neurons use plasticity of AIS length and/or location to regulate their intrinsic excitability. Here we quantify the impact of neuron morphology on AIS plasticity using computational models of simplified and realistic somatodendritic morphologies.
    [Show full text]
  • Satellite Glial Cell Communication in Dorsal Root Ganglia
    Neuronal somatic ATP release triggers neuron– satellite glial cell communication in dorsal root ganglia X. Zhang, Y. Chen, C. Wang, and L.-Y. M. Huang* Department of Neuroscience and Cell Biology, University of Texas Medical Branch, Galveston, TX 77555-1069 Edited by Charles F. Stevens, The Salk Institute for Biological Studies, La Jolla, CA, and approved April 25, 2007 (received for review December 14, 2006) It has been generally assumed that the cell body (soma) of a release of ATP from the somata of DRG neurons. Here, we show neuron, which contains the nucleus, is mainly responsible for that electric stimulation elicits robust vesicular release of ATP from synthesis of macromolecules and has a limited role in cell-to-cell neuronal somata and thus triggers bidirectional communication communication. Using sniffer patch recordings, we show here that between neurons and satellite cells. electrical stimulation of dorsal root ganglion (DRG) neurons elicits robust vesicular ATP release from their somata. The rate of release Results events increases with the frequency of nerve stimulation; external We asked first whether vesicular release of ATP occurs in the -Ca2؉ entry is required for the release. FM1–43 photoconversion somata of DRG neurons. P2X2-EGFP receptors were overex analysis further reveals that small clear vesicles participate in pressed in HEK cells and used as the biosensor (i.e., sniffer patch exocytosis. In addition, the released ATP activates P2X7 receptors method) (20). P2X2 receptors were chosen because they were easily in satellite cells that enwrap each DRG neuron and triggers the expressed at a high level (Ϸ200 pA/pF) in HEK cells and the communication between neuronal somata and glial cells.
    [Show full text]
  • Using the Modified Back-Propagation Algorithm to Perform Automated Downlink Analysis by Nancy Y
    Using The Modified Back-propagation Algorithm To Perform Automated Downlink Analysis by Nancy Y. Xiao Submitted to the Department of Electrical Engineering and Computer Science in partial fulfillment of the requirements for the degrees of Bachelor of Science and Master of Engineering in Electrical Engineering and Computer Science at the MASSACHUSETTS INSTITUTE OF TECHNOLOGY June 1996 Copyright Nancy Y. Xiao, 1996. All rights reserved. The author hereby grants to MIT permission to reproduce and distribute publicly paper and electronic copies of this thesis document in whole or in part, and to grant others the right to do so. A uthor ....... ............ Depar -uter Science May 28, 1996 Certified by. rnard C. Lesieutre ;rical Engineering Thesis Supervisor Accepted by.. F.R. Morgenthaler Chairman, Departmental Committee on Graduate Students OF TECH NOLOCG JUN 111996 Eng, Using The Modified Back-propagation Algorithm To Perform Automated Downlink Analysis by Nancy Y. Xiao Submitted to the Department of Electrical Engineering and Computer Science on May 28, 1996, in partial fulfillment of the requirements for the degrees of Bachelor of Science and Master of Engineering in Electrical Engineering and Computer Science Abstract A multi-layer neural network computer program was developed to perform super- vised learning tasks. The weights in the neural network were found using the back- propagation algorithm. Several modifications to this algorithm were also implemented to accelerate error convergence and optimize search procedures. This neural network was used mainly to perform pattern recognition tasks. As an initial test of the system, a controlled classical pattern recognition experiment was conducted using the X and Y coordinates of the data points from two to five possibly overlapping Gaussian distributions, each with a different mean and variance.
    [Show full text]
  • Was Not Reached, However, Even After Six to Sevenhours. A
    PROTEIN SYNTHESIS IN THE ISOLATED GIANT AXON OF THE SQUID* BY A. GIUDITTA,t W.-D. DETTBARN,t AND MIROSLAv BRZIN§ MARINE BIOLOGICAL LABORATORY, WOODS HOLE, MASSACHUSETTS Communicated by David Nachmansohn, February 2, 1968 The work of Weiss and his associates,1-3 and more recently of a number of other investigators,4- has established the occurrence of a flux of materials from the soma of neurons toward the peripheral regions of the axon. It has been postulated that this mechanism would account for the origin of most of the axonal protein, although the time required to cover the distance which separates some axonal tips from their cell bodies would impose severe delays.4 On the other hand, a number of observations7-9 have indicated the occurrence of local mechanisms of synthesis in peripheral axons, as suggested by the kinetics of appearance of individual proteins after axonal transection. In this paper we report the incorporation of radioactive amino acids into the protein fraction of the axoplasm and of the axonal envelope obtained from giant axons of the squid. These axons are isolated essentially free from small fibers and connective tissue, and pure samples of axoplasm may be obtained by extru- sion of the axon. Incorporation of amino acids into axonal protein has recently been reported using systems from mammals'0 and fish."I Materials and Methods.-Giant axons of Loligo pealii were dissected and freed from small fibers: they were tied at both ends. Incubations were carried out at 18-20° in sea water previously filtered through Millipore which contained 5 mM Tris pH 7.8 and 10 Muc/ml of a mixture of 15 C'4-labeled amino acids (New England Nuclear Co., Boston, Mass.).
    [Show full text]
  • Deep Multiphysics and Particle–Neuron Duality: a Computational Framework Coupling (Discrete) Multiphysics and Deep Learning
    applied sciences Article Deep Multiphysics and Particle–Neuron Duality: A Computational Framework Coupling (Discrete) Multiphysics and Deep Learning Alessio Alexiadis School of Chemical Engineering, University of Birmingham, Birmingham B15 2TT, UK; [email protected]; Tel.: +44-(0)-121-414-5305 Received: 11 November 2019; Accepted: 6 December 2019; Published: 9 December 2019 Featured Application: Coupling First-Principle Modelling with Artificial Intelligence. Abstract: There are two common ways of coupling first-principles modelling and machine learning. In one case, data are transferred from the machine-learning algorithm to the first-principles model; in the other, from the first-principles model to the machine-learning algorithm. In both cases, the coupling is in series: the two components remain distinct, and data generated by one model are subsequently fed into the other. Several modelling problems, however, require in-parallel coupling, where the first-principle model and the machine-learning algorithm work together at the same time rather than one after the other. This study introduces deep multiphysics; a computational framework that couples first-principles modelling and machine learning in parallel rather than in series. Deep multiphysics works with particle-based first-principles modelling techniques. It is shown that the mathematical algorithms behind several particle methods and artificial neural networks are similar to the point that can be unified under the notion of particle–neuron duality. This study explains in detail the particle–neuron duality and how deep multiphysics works both theoretically and in practice. A case study, the design of a microfluidic device for separating cell populations with different levels of stiffness, is discussed to achieve this aim.
    [Show full text]
  • Neural Network Architectures and Activation Functions: a Gaussian Process Approach
    Fakultät für Informatik Neural Network Architectures and Activation Functions: A Gaussian Process Approach Sebastian Urban Vollständiger Abdruck der von der Fakultät für Informatik der Technischen Universität München zur Erlangung des akademischen Grades eines Doktors der Naturwissenschaften (Dr. rer. nat.) genehmigten Dissertation. Vorsitzender: Prof. Dr. rer. nat. Stephan Günnemann Prüfende der Dissertation: 1. Prof. Dr. Patrick van der Smagt 2. Prof. Dr. rer. nat. Daniel Cremers 3. Prof. Dr. Bernd Bischl, Ludwig-Maximilians-Universität München Die Dissertation wurde am 22.11.2017 bei der Technischen Universtät München eingereicht und durch die Fakultät für Informatik am 14.05.2018 angenommen. Neural Network Architectures and Activation Functions: A Gaussian Process Approach Sebastian Urban Technical University Munich 2017 ii Abstract The success of applying neural networks crucially depends on the network architecture being appropriate for the task. Determining the right architecture is a computationally intensive process, requiring many trials with different candidate architectures. We show that the neural activation function, if allowed to individually change for each neuron, can implicitly control many aspects of the network architecture, such as effective number of layers, effective number of neurons in a layer, skip connections and whether a neuron is additive or multiplicative. Motivated by this observation we propose stochastic, non-parametric activation functions that are fully learnable and individual to each neuron. Complexity and the risk of overfitting are controlled by placing a Gaussian process prior over these functions. The result is the Gaussian process neuron, a probabilistic unit that can be used as the basic building block for probabilistic graphical models that resemble the structure of neural networks.
    [Show full text]