Efficient Almost Wait-Free Parallel Accessible Dynamic Hashtables 1
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Special Forces' Wear of Non-Standard Uniforms*
Special Forces’ Wear of Non-Standard Uniforms* W. Hays Parks** In February 2002, newspapers in the United States and United Kingdom published complaints by some nongovernmental organizations (“NGOs”) about US and other Coalition special operations forces operating in Afghanistan in “civilian clothing.”1 The reports sparked debate within the NGO community and among military judge advocates about the legality of such actions.2 At the US Special Operations Command (“USSOCOM”) annual Legal Conference, May 13–17, 2002, the judge advocate debate became intense. While some attendees raised questions of “illegality” and the right or obligation of special operations forces to refuse an “illegal order” to wear “civilian clothing,” others urged caution.3 The discussion was unclassified, and many in the room were not * Copyright © 2003 W. Hays Parks. ** Law of War Chair, Office of General Counsel, Department of Defense; Special Assistant for Law of War Matters to The Judge Advocate General of the Army, 1979–2003; Stockton Chair of International Law, Naval War College, 1984–1985; Colonel, US Marine Corps Reserve (Retired); Adjunct Professor of International Law, Washington College of Law, American University, Washington, DC. The views expressed herein are the personal views of the author and do not necessarily reflect an official position of the Department of Defense or any other agency of the United States government. The author is indebted to Professor Jack L. Goldsmith for his advice and assistance during the research and writing of this article. 1 See, for example, Michelle Kelly and Morten Rostrup, Identify Yourselves: Coalition Soldiers in Afghanistan Are Endangering Aid Workers, Guardian (London) 19 (Feb 1, 2002). -
Polimetriche Per Linea STIBM Area Nord.Xlsx
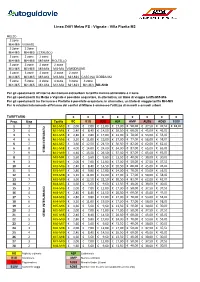
Linea Z401 Melzo FS - Vignate - Villa Fiorita M2 MELZO 2 zone Mi4-Mi5 VIGNATE 2 zone 2 zone Mi4-Mi5 Mi4-Mi5 CERNUSCO 2 zone 2 zone 2 zone Mi4-Mi5 Mi4-Mi5 Mi3-Mi4 PIOLTELLO 3 zone 3 zone 2 zone 2 zone Mi3-Mi5 Mi3-Mi5 Mi3-Mi4 Mi3-Mi4 VIMODRONE 3 zone 3 zone 2 zone 2 zone 2 zone Mi3-Mi5 Mi3-Mi5 Mi3-Mi4 Mi3-Mi4 Mi3-Mi4 CASCINA GOBBA M2 5 zone 5 zone 4 zone 4 zone 3 zone 3 zone Mi1-Mi5 Mi1-Mi5 Mi1-Mi4 Mi1-Mi4 Mi1-Mi3 Mi1-Mi3 MILANO Per gli spostamenti all'interno dei Comuni extraurbani la tariffa minima utilizzabile è 2 zone Per gli spostamenti tra Melzo e Vignate è possibile acquistare, in alternativa, un titolo di viaggio tariffa Mi5-Mi6 Per gli spostamenti tra Cernusco e Pioltello è possibile acquistare, in alternativa, un titolo di viaggio tariffa Mi4-Mi5 Per le relazioni interamente all'interno dei confini di Milano è ammesso l'utilizzo di mensili e annuali urbani TARIFFARIO €€€€€€€€ Prog. Ring Tariffa BO B1G B3G ASP AMP AU26 AO65 B10V 1 3 Mi1-Mi3 € 2,00 € 7,00 € 12,00 € 17,00 € 50,00 € 37,50 € 37,50 € 18,00 2 4 Mi1-Mi4 € 2,40 € 8,40 € 14,50 € 20,50 € 60,00 € 45,00 € 45,00 3 5 Mi1-Mi5 € 2,80 € 9,80 € 17,00 € 24,00 € 70,00 € 53,00 € 53,00 4 6 Mi1-Mi6 € 3,20 € 11,00 € 19,00 € 27,00 € 77,00 € 58,00 € 58,00 5 7 Mi1-Mi7 € 3,60 € 12,50 € 21,50 € 30,50 € 82,00 € 62,00 € 62,00 6 8 Mi1-Mi8 € 4,00 € 14,00 € 24,00 € 34,00 € 87,00 € 65,00 € 65,00 7 9STIBM INTEGRATO Mi1-Mi9€ 4,40 € 15,50 € 26,50 € 37,50 € 87,00 € 65,00 € 65,00 8 2 MI3-MI4 € 1,60 € 5,60 € 9,60 € 13,50 € 40,00 € 30,00 € 30,00 9 3 MI3-MI5 € 2,00 € 7,00 € 12,00 € 17,00 € 50,00 € 37,50 -

I Was Happy and Flattered to Be Invited to Deliver This Lecture Because Like So Many Others Who Knew Michael Quinlan I Was an Impassioned Admirer
I was happy and flattered to be invited to deliver this lecture because like so many others who knew Michael Quinlan I was an impassioned admirer. Yet I cannot this evening avoid being a little daunted by the memory of an occasion twenty years ago, when we both attended a talk given by a general newly returned from the Balkans. Michael said to me afterwards: ‘Such a pity, isn’t it, when a soldier who has done really quite well on a battlefield simply lacks the intellectual firepower to explain coherently afterwards what he has been doing’. Few of us, alas, possess the ‘intellectual firepower’ to meet Michael’s supremely and superbly exacting standard. I am a hybrid, a journalist who has written much about war as a reporter and commentator; and also a historian. I am not a specialist in intelligence, either historic or contemporary. By the nature of my work, however, I am a student of the intelligence community’s impact upon the wars both of the 20th century and of our own times. I have recently researched and published a book about the role of intelligence in World War II, which confirmed my impression that while the trade employs some clever people, it also attracts some notably weird ones, though maybe they would say the same about historians. Among my favourite 1939-45 vignettes, there was a Japanese spy chief whose exploits caused him to be dubbed by his own men Lawrence of Manchuria. Meanwhile a German agent in Stockholm warned Berlin in September 1944 that the allies were about to stage a mass parachute drop to seize a Rhine bridge- the Arnhem operation. -

1 Introduction
Notes 1 Introduction 1. Donald Macintyre, Narvik (London: Evans, 1959), p. 15. 2. See Olav Riste, The Neutral Ally: Norway’s Relations with Belligerent Powers in the First World War (London: Allen and Unwin, 1965). 3. Reflections of the C-in-C Navy on the Outbreak of War, 3 September 1939, The Fuehrer Conferences on Naval Affairs, 1939–45 (Annapolis: Naval Institute Press, 1990), pp. 37–38. 4. Report of the C-in-C Navy to the Fuehrer, 10 October 1939, in ibid. p. 47. 5. Report of the C-in-C Navy to the Fuehrer, 8 December 1939, Minutes of a Conference with Herr Hauglin and Herr Quisling on 11 December 1939 and Report of the C-in-C Navy, 12 December 1939 in ibid. pp. 63–67. 6. MGFA, Nichols Bohemia, n 172/14, H. W. Schmidt to Admiral Bohemia, 31 January 1955 cited by Francois Kersaudy, Norway, 1940 (London: Arrow, 1990), p. 42. 7. See Andrew Lambert, ‘Seapower 1939–40: Churchill and the Strategic Origins of the Battle of the Atlantic, Journal of Strategic Studies, vol. 17, no. 1 (1994), pp. 86–108. 8. For the importance of Swedish iron ore see Thomas Munch-Petersen, The Strategy of Phoney War (Stockholm: Militärhistoriska Förlaget, 1981). 9. Churchill, The Second World War, I, p. 463. 10. See Richard Wiggan, Hunt the Altmark (London: Hale, 1982). 11. TMI, Tome XV, Déposition de l’amiral Raeder, 17 May 1946 cited by Kersaudy, p. 44. 12. Kersaudy, p. 81. 13. Johannes Andenæs, Olav Riste and Magne Skodvin, Norway and the Second World War (Oslo: Aschehoug, 1966), p. -

A Visual Motion Detection Circuit Suggested by Drosophila Connectomics
ARTICLE doi:10.1038/nature12450 A visual motion detection circuit suggested by Drosophila connectomics Shin-ya Takemura1, Arjun Bharioke1, Zhiyuan Lu1,2, Aljoscha Nern1, Shiv Vitaladevuni1, Patricia K. Rivlin1, William T. Katz1, Donald J. Olbris1, Stephen M. Plaza1, Philip Winston1, Ting Zhao1, Jane Anne Horne2, Richard D. Fetter1, Satoko Takemura1, Katerina Blazek1, Lei-Ann Chang1, Omotara Ogundeyi1, Mathew A. Saunders1, Victor Shapiro1, Christopher Sigmund1, Gerald M. Rubin1, Louis K. Scheffer1, Ian A. Meinertzhagen1,2 & Dmitri B. Chklovskii1 Animal behaviour arises from computations in neuronal circuits, but our understanding of these computations has been frustrated by the lack of detailed synaptic connection maps, or connectomes. For example, despite intensive investigations over half a century, the neuronal implementation of local motion detection in the insect visual system remains elusive. Here we develop a semi-automated pipeline using electron microscopy to reconstruct a connectome, containing 379 neurons and 8,637 chemical synaptic contacts, within the Drosophila optic medulla. By matching reconstructed neurons to examples from light microscopy, we assigned neurons to cell types and assembled a connectome of the repeating module of the medulla. Within this module, we identified cell types constituting a motion detection circuit, and showed that the connections onto individual motion-sensitive neurons in this circuit were consistent with their direction selectivity. Our results identify cellular targets for future functional investigations, and demonstrate that connectomes can provide key insights into neuronal computations. Vision in insects has been subject to intense behavioural1,physiological2 neuroanatomy14. Given the time-consuming nature of such recon- and anatomical3 investigations, yet our understanding of its underlying structions, we wanted to determine the smallest medulla volume, neural computations is still far from complete. -

The Baghdad Set
The Baghdad Set Also by Adrian O’Sullivan: Nazi Secret Warfare in Occupied Persia (Iran): The Failure of the German Intelligence Services, 1939–45 (Palgrave, 2014) Espionage and Counterintelligence in Occupied Persia (Iran): The Success of the Allied Secret Services, 1941–45 (Palgrave, 2015) Adrian O’Sullivan The Baghdad Set Iraq through the Eyes of British Intelligence, 1941–45 Adrian O’Sullivan West Vancouver, BC, Canada ISBN 978-3-030-15182-9 ISBN 978-3-030-15183-6 (eBook) https://doi.org/10.1007/978-3-030-15183-6 Library of Congress Control Number: 2019934733 © The Editor(s) (if applicable) and The Author(s), under exclusive licence to Springer Nature Switzerland AG 2019 This work is subject to copyright. All rights are solely and exclusively licensed by the Publisher, whether the whole or part of the material is concerned, specifically the rights of translation, reprinting, reuse of illustrations, recitation, broadcasting, reproduction on microfilms or in any other physical way, and transmission or information storage and retrieval, electronic adaptation, computer software, or by similar or dissimilar methodology now known or hereafter developed. The use of general descriptive names, registered names, trademarks, service marks, etc. in this publication does not imply, even in the absence of a specific statement, that such names are exempt from the relevant protective laws and regulations and therefore free for general use. The publisher, the authors and the editors are safe to assume that the advice and information in this book are believed to be true and accurate at the date of publication. Neither the pub- lisher nor the authors or the editors give a warranty, express or implied, with respect to the material contained herein or for any errors or omissions that may have been made. -

Churchill's Diplomatic Eavesdropping and Secret Signals Intelligence As
CHURCHILL’S DIPLOMATIC EAVESDROPPING AND SECRET SIGNALS INTELLIGENCE AS AN INSTRUMENT OF BRITISH FOREIGN POLICY, 1941-1944: THE CASE OF TURKEY Submitted for the Degree of Ph.D. Department of History University College London by ROBIN DENNISTON M.A. (Oxon) M.Sc. (Edin) ProQuest Number: 10106668 All rights reserved INFORMATION TO ALL USERS The quality of this reproduction is dependent upon the quality of the copy submitted. In the unlikely event that the author did not send a complete manuscript and there are missing pages, these will be noted. Also, if material had to be removed, a note will indicate the deletion. uest. ProQuest 10106668 Published by ProQuest LLC(2016). Copyright of the Dissertation is held by the Author. All rights reserved. This work is protected against unauthorized copying under Title 17, United States Code. Microform Edition © ProQuest LLC. ProQuest LLC 789 East Eisenhower Parkway P.O. Box 1346 Ann Arbor, Ml 48106-1346 2 ABSTRACT Churchill's interest in secret signals intelligence (sigint) is now common knowledge, but his use of intercepted diplomatic telegrams (bjs) in World War Two has only become apparent with the release in 1994 of his regular supply of Ultra, the DIR/C Archive. Churchill proves to have been a voracious reader of diplomatic intercepts from 1941-44, and used them as part of his communication with the Foreign Office. This thesis establishes the value of these intercepts (particularly those Turkey- sourced) in supplying Churchill and the Foreign Office with authentic information on neutrals' response to the war in Europe, and analyses the way Churchill used them. -

Monday/Tuesday Playoff Schedule
2013 TUC MONDAY/TUESDAY PLAYOFF MASTER FIELD SCHEDULE Start End Hockey1 Hockey2 Hockey3 Hockey4 Hockey5 Ulti A Soccer 3A Soccer 3B Cricket E1 Cricket E2 Cricket N1 Cricket N2 Field X 8:00 9:15 MI13 MI14 TI13 TI14 TI15 TI16 MI1 MI2 MI3 MI4 MI15 MI16 9:20 10:35 MI17 MI18 TI17 TI18 TI19 TI20 MI5 MI6 10:40 11:55 MI19 MI20 MC1 MC2 MC3 MI21 MI7 MI8 12:00 1:15 MI9* TI21* TI22 TI23 TI24 MI10 MI11 MI12 1:20 2:35 MI22 MC4 MC6 MC5 MI23 TC1 MI24 MI25 2:40 3:55 TI1 TI2 MC7 TI3 MI26 TC2 TR1 TR2 MI27 4:00 5:15 MC8* TC3 MC10 MC9 TI4 TC4 TR3 TR4 5:20 6:35 TC5* TI5 TI6 TI7 TI8 TC6 TR5 TR6 6:40 7:55 TI9* TC7 TI10 TI11 TI12 TC8 TR8 TR7 Games are to 15 points Half time at 8 points Games are 1 hour and 15 minutes long Soft cap is 10 minutes before the end of game, +1 to highest score 2 Timeouts per team, per game NO TIMEOUTS AFTER SOFT CAP Footblocks not allowed, unless captains agree otherwise 2013 TUC Monday Competitive Playoffs - 1st to 7th Place 3rd Place Bracket Loser of MC4 Competitive Teams Winner of MC9 MC9 Allth Darth (1) Allth Darth (1) 3rd Place Slam Dunks (2) Loser of MC5 The Ligers (3) Winner of MC4 MC4 Krash Kart (4) Krash Kart (4) The El Guapo Sausage Party (5) MC1 Wonky Pooh (6) Winner of MC1 Disc Horde (7) The El Guapo Sausage Winner of MC8 Party (5) MC8 Slam Dunks (2) Champions Winner of MC2 MC2 Disc Horde (7) MC5 The Ligers (3) Winner of MC5 MC3 Winner of MC3 Wonky Pooh (6) Time Hockey3 Score Spirit Hockey4 Score Spirit Hockey5 Score Spirit Score Spirit 10:40 Krash Kart (4) Slam Dunks (2) The Ligers (3) to vs. -

Evolution of Stickleback in 50 Years on Earthquake-Uplifted Islands
Evolution of stickleback in 50 years on earthquake-uplifted islands Emily A. Lescaka,b, Susan L. Basshamc, Julian Catchenc,d, Ofer Gelmondb,1, Mary L. Sherbickb, Frank A. von Hippelb, and William A. Creskoc,2 aSchool of Fisheries and Ocean Sciences, University of Alaska Fairbanks, Fairbanks, AK 99775; bDepartment of Biological Sciences, University of Alaska Anchorage, Anchorage, AK 99508; cInstitute of Ecology and Evolution, University of Oregon, Eugene, OR 97403; and dDepartment of Animal Biology, University of Illinois at Urbana–Champaign, Urbana, IL 61801 Edited by John C. Avise, University of California, Irvine, CA, and approved November 9, 2015 (received for review June 19, 2015) How rapidly can animal populations in the wild evolve when faced occur immediately after a habitat shift or environmental distur- with sudden environmental shifts? Uplift during the 1964 Great bance (26, 27). However, because of previous technological lim- Alaska Earthquake abruptly created freshwater ponds on multiple itations, few studies of rapid differentiation in the wild have islands in Prince William Sound and the Gulf of Alaska. In the short included genetic data to fully disentangle evolution from induced time since the earthquake, the phenotypes of resident freshwater phenotypic plasticity. The small numbers of markers previously threespine stickleback fish on at least three of these islands have available for most population genetic studies have not provided changed dramatically from their oceanic ancestors. To test the the necessary precision with which to analyze very recently diverged hypothesis that these freshwater populations were derived from populations (but see refs. 28 and 29). As a consequence, the fre- oceanic ancestors only 50 y ago, we generated over 130,000 single- quency of contemporary evolution in the wild is still poorly defined, nucleotide polymorphism genotypes from more than 1,000 individ- and its genetic and genomic basis remains unclear (30). -

The Detention of Non-Enemy Civilians Escaping to Britain During the Second World War
The Historical Journal (2021), 1–23 doi:10.1017/S0018246X2100008X ARTICLE The Detention of Non-Enemy Civilians Escaping to Britain during the Second World War Artemis J. Photiadou Department of International History, London School of Economics and Political Science, London, UK E-mail: [email protected] Abstract Thousands of civilians from Allied and neutral countries reached Britain during the Second World War. Nearly all who arrived between 1941 and 1945 were detained for interrogation – an unprecedented course of action by Britain which has nevertheless seldomly been studied. This article focuses on the administrative history of this process and the people it affected. It demonstrates how certain parts of the state treated non- Britons with suspicion throughout the war, long after fears of a ‘fifth column’ had sub- sided. At the same time, others saw them favourably, not least because many either offered intelligence, intended to volunteer with the Allied Forces, or work for the war industry. Examining how these conflicting views co-existed within a single deten- tion camp, this article thus illustrates the complex relationship that existed between non-Britons and the wartime state, which perceived them simultaneously as suspects, assets, and allies. By making use of the thousands of resulting interrogation reports, the article also offers more detail than currently exists on the gender and nationality background of those who reached Britain, as well as about the journeys they took to escape occupied territory. Chaim Wasserman, a young Jewish man from Poland, was in a detention camp in London when the war in Europe ended. The camp authorities described him as a student, but that had been his status six years earlier, when at the age of eighteen he was sent to live in a ghetto in Warsaw, then to several prison camps, then to Auschwitz, and eventually to Buchenwald, from where he escaped in April 1945. -

Church Cmte Book VI: Part Two: the Middle Years (1914-1939)
PART Two THEMIDDLE YEARS (1914-1939) Sometime in 1915 the Japanese warship Amma went aground in Turtle Bay in the Gulf of Lower California. The presence of this vessel in that part of the world was not a total surprise as Japanese fleet units had been previously sighted a few times in the area. Earlier the Grand admiral of Sippon had paid a visit to Mexico, expounding a blood brother theme. What appeared to be somewhat incredible about this incident was that the formidable veterans of Tsushima could be so inept as to allow this accident to happen. Indeed, it sub- sequently became questionable that the event was an accident at all. According to Sidney Nashbir, an intelligence officer destined to gain fame with General Douglas MacArthur’s Allied Translator and Inter- preter Section during World WTar II, there were “unquestionable proofs that whole companies of Japanese soldiers had traversed a part of southern Arizona in 1916 during secret exercises, proceedings that could only have been associated with the Asam’s wallowing in the mud the previous year.” As an intelligence officer in 1916 with the First Arizona Infantry he had been detailed by that General Funston of Aguinaldo fame on a mission to seek the truth of rumors among Indians of Japanese columns present in northern Sonora in Mexico. Mashbir, who later acted as a gpy for America in Manchuria., tramped across the desert (which he knew well enough to make tihe first map of it our Army ever had). His knowledge of the desert told him that even the Japanese, incredible marchers that they were, could not ,have made the trip without violating Arizona territory to the north for water. -

2014 Tuc Monday/Tuesday Playoff Master Field Schedule
2014 TUC MONDAY/TUESDAY PLAYOFF MASTER FIELD SCHEDULE Start End Hockey 1 Hockey 2 Hockey 3 Hockey 4 Hockey 5 Hockey 6 Ulti A Rugby E1 Rugby E2 9:20 10:35 MI1 MI2 MC1 MC2 MI8 MI9 10:40 11:55 MI3 MI4 MC5 MC3 MC4 MI11 MI5 MI10 12:00 1:15 MI6 MI7 MC7 1:30 2:55 ASI1 ASI2 ASC1 ASC2 MC6 3:00 4:25 ASI3 ASI4 ASC4 ASC3 4:30 5:45 T5 T6 T2 T1 5:50 7:05 T7 T8 T4 T3 TOURNAMENT RULES Games are to 15 points Half time at 8 points Playoff games are 1 hour and 15 minutes long Hard cap is at 75 minutes (finish the point, only if tied do you play another), and there is no soft cap. 1 Timeout per half, per team (no timeouts if in overtime) Footblocks are not allowed, unless captains agree otherwise 2014 TUC Monday Competitive Playoffs - 1st to 6th Place Teams 3rd Place Deep (1) Deep (1) L - MC3 Allth Darth (2) 3rd Place MC7 naptime (3) W - MC3 MC3 Slam Dunks (4) Slam Dunks (4) L - MC4 El Guapo (5) MC1 Basic Bishes (6) W - MC1 5th Place El Guapo (5) Champions L - MC1 MC6 5th Place MC5 Allth Darth (2) L - MC2 MC4 naptime (3) W - MC4 MC2 W - MC2 Basic Bishes (6) Time Hockey 4 Score Spirit Hockey 6 Score Spirit 9:20 Slam Dunks (4) naptime (3) to vs. MC 1 vs. MC 2 10:35 El Guapo (5) Basic Bishes (6) Time Hockey 4 Score Spirit Hockey 6 Score Spirit Hockey 3 Score Spirit 10:40 Deep (1) Allth Darth (2) L - MC1 to vs.