Can Culling to Prevent Monkeypox Infection Be Counter-Productive? Scenarios from a Theoretical Model
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

WHO | World Health Organization
WHO/CDS/CSR/99.1 Report of the meeting of the Ad Hoc Committee on Orthopoxvirus Infections. Geneva, Switzerland, 14-15 January 1999 World Health Organization Department of Communicable Disease Surveillance and Response This document has been downloaded from the WHO/CSR Web site. The original cover pages and lists of participants are not included. See http://www.who.int/emc for more information. © World Health Organization This document is not a formal publication of the World Health Organization (WHO), and all rights are reserved by the Organization. The document may, however, be freely reviewed, abstracted, reproduced and translated, in part or in whole, but not for sale nor for use in conjunction with commercial purposes. The views expressed in documents by named authors are solely the responsibility of those authors. The mention of specific companies or specific manufacturers' products does no imply that they are endorsed or recommended by the World Health Organization in preference to others of a similar nature that are not mentioned. Contents Introduction 1 Recent monkeypox outbreaks in the Democratic Republic of Congo 1 Review of the report of the 1994 Ad Hoc Committee on Orthopoxvirus Infections 2 Work in WHO Collaborating Centres 3 Analysis and sequencing of variola virus genomes 3 Biosecurity and physical security of WHO collaborating laboratories 4 Smallpox vaccine stocks and production 4 Deliberate release of smallpox virus 4 Survey of WHO Member States latest position on destruction of variola virus 4 Recommendations 5 List of Participants 6 Page i REPORT OF THE MEETING OF THE AD HOC COMMITTEE ON ORTHOPOXVIRUS INFECTIONS Geneva, Switzerland 14-15 January 1999 Introduction Dr Lindsay Martinez, Director, Communicable Disease Surveillance and Response (CSR), welcomed participants and opened the meeting on behalf of the Director-General of WHO, Dr G.H. -

A Tale of Two Viruses: Coinfections of Monkeypox and Varicella Zoster Virus in the Democratic Republic of Congo
Am. J. Trop. Med. Hyg., 104(2), 2021, pp. 604–611 doi:10.4269/ajtmh.20-0589 Copyright © 2021 by The American Society of Tropical Medicine and Hygiene A Tale of Two Viruses: Coinfections of Monkeypox and Varicella Zoster Virus in the Democratic Republic of Congo Christine M. Hughes,1* Lindy Liu,2,3 Whitni B. Davidson,1 Kay W. Radford,4 Kimberly Wilkins,1 Benjamin Monroe,1 Maureen G. Metcalfe,3 Toutou Likafi,5 Robert Shongo Lushima,6 Joelle Kabamba,7 Beatrice Nguete,5 Jean Malekani,8 Elisabeth Pukuta,9 Stomy Karhemere,9 Jean-Jacques Muyembe Tamfum,9 Emile Okitolonda Wemakoy,5 Mary G. Reynolds,1 D. Scott Schmid,4 and Andrea M. McCollum1 1Poxvirus and Rabies Branch, Division of High-Consequence Pathogens and Pathology, National Center for Emerging and Zoonotic Infectious Diseases, U.S. Centers for Disease Control and Prevention, Atlanta, Georgia; 2Bacterial Special Pathogens Branch, Division of High-Consequence Pathogens and Pathology, National Center for Emerging and Zoonotic Infectious Diseases, U.S. Centers for Disease Control and Prevention, Atlanta, Georgia; 3Infectious Diseases Pathology Branch, Division of High-Consequence Pathogens and Pathology, National Center for Emerging and Zoonotic Infectious Diseases, U.S. Centers for Disease Control and Prevention, Atlanta, Georgia; 4Viral Vaccine Preventable Diseases Branch, Division of Viral Diseases, National Center for Immunizations and Respiratory Diseases, U.S. Centers for Disease Control and Prevention, Atlanta, Georgia; 5Kinshasa School of Public Health, Kinshasa, Democratic Republic of Congo; 6Ministry of Health, Kinshasa, Democratic Republic of Congo; 7U.S. Centers for Disease Control and Prevention, Kinshasa, Democratic Republic of Congo; 8Department of Biology, University of Kinshasa, Kinshasa, Democratic Republic of Congo; 9Institut National de Recherche Biomedicale, ´ Kinshasa, Democratic Republic of Congo Abstract. -

Fact Sheet: Basic Information About Monkeypox
MONKEYPOX FACT SHEET Basic Information about Monkeypox Monkeypox: An Emerging Infectious Disease in North America Monkeypox is a rare viral disease that is found mostly in the rainforest countries of central and west Africa. The disease is called “monkeypox” because it was first discovered in laboratory monkeys in 1958. Blood tests of animals in Africa later found evidence of monkeypox infection in various rodent species. The virus that causes monkeypox was recovered from an African squirrel, which may be the natural host. Laboratory studies showed that the virus could also infect rats, mice, and rabbits. In 1970, monkeypox was identified as the cause of a rash illness in humans in remote African locations. In early June 2003, monkeypox was reported among several residents in the United States who became ill after having contact with sick pet prairie dogs. This is the first evidence of community-acquired monkeypox in the United States. Cause of Monkeypox The disease is caused by Monkeypox virus, which belongs to the orthopoxvirus group of viruses. Other orthopoxviruses that can cause infection in humans include variola (smallpox), vaccinia (used in smallpox vaccine), and cowpox viruses. Signs and Symptoms In humans, the signs and symptoms of monkeypox are similar to those of smallpox, but usually milder. Unlike smallpox, monkeypox causes swollen lymph nodes. The incubation period for monkeypox is about 12 days.The illness begins with fever, headache, muscle aches, backache, swollen lymph nodes, a general feeling of discomfort, and exhaustion. Within 1 to 3 days (sometimes longer) after onset of fever, the patient develops a papular rash (i.e., raised bumps), often first on the face but sometimes initially on other parts of the body. -
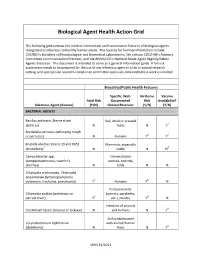
Biological Agent Health Action Grid
Biological Agent Health Action Grid The following grid summarizes medical intervention and transmission features of biological agents recognized as infectious to healthy human adults. The sources for foonote information include: CDC/NIH’s Biosafety in Microbiological and Biomedical Laboratories, 5th edition; CDC/HHS’s Advisory Committee on Immunization Practices; and the APHIS/CDC’s National Select Agent Registry/Select Agents Exclusion. This document is intended to serve as a general information guide. A full risk assessment needs to be prepared for the use of any infectious agent in a lab or animal research setting, and appropriate research compliance committee approvals obtained before work is initiated. Biosafety/Public Health Features Specific, Well- Air-Borne Vaccine Fetal Risk Documented Risk Availability? Infectious Agent (disease) (Y/N) Natural Reservoir (Y/N) (Y/N) BACTERIAL AGENTS Bacillus anthracis, Sterne strain Soil, dried or pressed (anthrax)1 N hides N Y2 Bordetella pertussis (whooping cough or pertussis) N Humans Y3 Y4 Brucella abortus Strains 19 and RB51 Mammals, especially (brucellosis)5 N cattle N N6 Campylobacter spp. Domesticated (campylobacteriosis, traveler's animals, rodents, diarrhea) N birds N N Chlamydia trachomatis, Chlamydia pneumoniae (lymphogranuloma venereum, trachoma, pneumonia) Y7 Humans Y8 N Psittacine birds Chlamydia psittaci (psittacosis or (parrots, parakeets, parrott fever) Y7 etc.), poultry Y8 N Intestine of animals Clostridium tetani (tetanus or lockjaw) N and humans N Y4 Soil contaminated Corynebacterium diphtheriae with animal/human (diphtheria) N feces N Y4 VEHS 11/2011 Specific, Well- Air-Borne Vaccine Fetal Risk Documented Risk Availability? Infectious Agent (disease) (Y/N) Natural Reservoir (Y/N) (Y/N) Francisella tularensis, subspecies Wild animals, esp. -

Aerosol Transmissible Disease Biosafety Plan
AEROSOL TRANSMISSIBLE DISEASE BIOSAFETY PLAN Principal Investigator: Department: Date: I. EXPOSURE DETERMINATION: A. The following organisms and viruses are covered. We recognize that there is a high degree of variability in infectivity of these organisms and viruses. Check √ the organism(s) or viruses used in your laboratory: Adenovirus Helicobacter pylori4 Parvovirus B19 Arboviruses1 Hemorrhagic fever viruses5 Prions8 Arenaviruses2 Hendra virus Rabies virus9 Bacillus anthracis3 Hepatitis B Virus Retroviruses10 Blastomyces dermatitidis Hepatitis C Virus Rickettsia akari Bordetella pertussis Hepatitis D virus Rickettsia australis Brucella abortus Herpes Simplex Virus 1 Rickettsia conorii Brucella canis Herpes Simplex Virus 2 Rickettsia japonicum Brucella maris Herpesvirus simiae (B-virus) Rickettsia prowazekii Brucella melitensis Histoplasma capsulatum Rickettsia rickettsii Brucella suis Human Herpesvirus 6A Rickettsia siberica Burkholderia mallei Human Herpesvirus 6B Rickettsia typhi Burkholderia pseudomallei Human Herpesvirus 7 Rickettsia tsutsuagmushi Chlamydia pneumoniae Human Herpesvirus 8 Rift Valley fever virus Chlamydia psittaci Influenza Viruses6 Rubella Virus Chlamydia trachomatis Junin virus Sabia virus Clostridium botulinum Kyasanur forest disease virus Salmonella species Coccidioides immitis Lassa fever virus Salmonella typhi Coccidioides posadasii Legionella pneumophila SARS coronavirus Corynebacterium diphtheriae Lymphocytic Choriomeningitis Virus Shigella species Coxiella burnetti Machupo virus Streptococcus species, group -

Monkeypox Virus Liberia, and the US (Ex-Ghana)
APPENDIX 2 Monkeypox Virus Liberia, and the US (ex-Ghana). The West African clade is less virulent than the Congo Basin clade. Disease Agent: Common Human Exposure Routes: • Monkeypox virus (MPV) • Respiratory, percutaneous, and permucosal expo- Disease Agent Characteristics: sures to infected monkeys, zoo animals, prairie dogs, and humans • Family: Poxviridae; Subfamily: Chordopoxvirinae; Genus: Orthopoxvirus Likelihood of Secondary Transmission: • Virion morphology and size: Enveloped, slightly pleomorphic; dumbbell-shaped core with lateral • Direct contact with body fluids, respiratory droplets, bodies; 140-260 nm in diameter by 220-450 nm in or with virus-contaminated objects, such as bedding length or clothing • Nucleic acid: linear, double-stranded DNA virus; • Period of human-to-human transmission is during genome length: ~197 kb in length bp the first week of the rash. • Physicochemical properties: Resistant to common • Longest chain of documented human-to-human phenolic disinfectants; inactivated with polar lipo- transmission was five generations (four serial philic solvents, such as chloroform, and at low pH. transmissions). Complete inactivation of the closely related vaccinia At-Risk Populations: virus occurs in 2-3 hours at 60°C or within minutes following exposure to 20 nM caprylate at 22°C; • Very low in the US, based on animal import controls however, MPV is more resistant than vaccinia to established in 2003 solvent-detergent treatment. • In Africa, people coming in contact with infected animals Disease Name: Vector and Reservoir Involved: • Monkeypox • Reservoir is African rodents Priority Level: Blood Phase: • Scientific/Epidemiologic evidence regarding blood safety: Theoretical • In an outbreak in the Republic of Congo, one out of • Public perception and/or regulatory concern regard- five specimens was positive after 21 days. -

Monkeypox Section 1: ABOUT the DISEASE
Guide to Surveillance, Reporting and Control Massachusetts Department of Public Health, Bureau of Communicable Disease Control Monkeypox Section 1: ABOUT THE DISEASE A. Etiologic Agent Monkeypox is a zoonotic disease caused by the monkeypox virus of the family Orthopoxviridae. This genus also includes variola virus (smallpox), vaccinia virus (the virus in the smallpox vaccine), and cowpox. The disease is called monkeypox because the agent was first discovered in laboratory monkeys in 1958, but the natural hosts of the virus are rodents. Note: Variola virus is covered in detail in the “Smallpox” chapter of this manual. B. Clinical Description The symptoms of monkeypox are similar to human smallpox, although they are milder. They include fever, headache, muscle aches, swollen lymph nodes, and fatigue. A rash typically develops within three days of the onset of fever. The rash typically becomes vesiculopustular (blisters with clear, progressing to cloudy, contents). The rash usually starts on the face, but may begin on other body parts. The raised bumps of the rash go through stages, much like the smallpox rash, before becoming crusted, scabbing, and falling off. The duration of illness ranges from 2–4 weeks. C. Vectors and Reservoirs Recent evidence suggests that African squirrels may be the natural reservoir for monkeypox, but other rodents including Gambian rats, mice, and the elephant shrew, and mammals including rabbits, monkeys, and pigs, can be carriers. D. Modes of Transmission Monkeypox is transmitted through direct contact with infected animals, including a bite from the animal as well as contact with the animal’s blood, body fluids, or rash. -

ORIGINAL ARTICLE AFRICAN JOURNAL of CLINICAL and EXPERIMENTAL MICROBIOLOGY MAY 2017 ISBN 1595�689X VOL18 No
ORIGINAL ARTICLE AFRICAN JOURNAL OF CLINICAL AND EXPERIMENTAL MICROBIOLOGY MAY 2017 ISBN 1595-689X VOL18 No. 2 AJCEM/1713 http://www.ajol.info/journals/ajcem COPYRIGHT 2017 https://dx.doi.org/10.4314/ajcem.v18i2.5 AFR. J. CLN. EXPER. MICROBIOL. 18 (2): 86- 91 MOLECULAR DIAGNOSTICS BY PCR OF POXVIRUSES ( ORTHOPOXVIRUS (OPV) AND MOLLUSCUM CONTAGIOSUM VIRUS (MCV)) IN CÔTE D'IVOIRE WEST AFRICA Meite S 1,2 , Coulibaly N. D 1, Boni-Cissé C 2, Koffi KS 2, Sylla A 1, Kouassi KS 1, Mlan AP 2, Kouame SM1, ZabaFS 3, Ngazoa KS 1, Faye-Ketté H 2, Dosso M2 1. Institut Pasteur Côte d’Ivoire, Platform of Molecular Biology, 2. Department of microbiology; Faculty of medical sciences FHB University Abidjan, 3. Laboratory of bacteriology virology , University hospital of Yopougon Abidjan Correspondence: 22 BP 539 Abidjan Côte d’Ivoire. E mail: [email protected] ABSTRACT The Orthopoxvirus (OPV) and the Molluscum contagiosum virus (MCV) are Poxviruses involved in viruses skin lesions in humans. OPV infects many vertebrates and MCV mainly infects humans. A diagnostic confusion is often observed between the clinical lesions due to the different Poxviruses firstly and secondly with other viruses like the virus of the chickenpox. In Côte d'Ivoire, the diagnosis of MCV remains essentially clinical and that of OPV is non-existent despite the risk of circulation of the virus. This study aims to implementthe molecular detection of the OPV and the MVC in Côte d'Ivoire. Material and method: Cowpoxvirus DNA and 21 DNA extracts from suspicious cutaneous lesions of the MCV were analyzed by conventional PCR. -

First Human Infection Case of Monkey B Virus Identified in China, 2021
China CDC Weekly Notes from the Field First Human Infection Case of Monkey B Virus Identified in China, 2021 Wenling Wang1,&; Wenjie Qi2,&; Jingyuan Liu3,&; Haijun Du4,&; Li Zhao1; Yang Zheng5; Guoxing Wang2; Yang Pan5; Baoying Huang1; Zhaomin Feng5; Daitao Zhang5; Peng Yang5; Jun Han4,#; Quanyi Wang5,#; Wenjie Tan1,# Monkey B virus (BV), initially isolated in 1932, is polymerase chain reaction (rtPCR) were performed to currently designated as Macacine alphaherpesvirus 1 by detect BV (3), varicella zoster virus (VZV) (4), the International Committee on Taxonomy of Viruses monkeypox virus and orthopoxvirus (5). For BV (1). BV is an alphaherpesvirus enzootic in macaques of detection, the forward primer was 5′-TGGCCTACTA the genus Macaca, normally transmitted horizontally CCGCGTGG-3′, the reverse primer was 5′-TGGTA via direct contact and exchange of bodily secretions, CGTGTGGGAGTAGCG-3′; and the TaqMan probe just like herpes simplex virus (HSV) in humans. BV is was 5′-FAM-CCGCCCTCTCCGAGCACGTG-TAM not evident in its natural macaque hosts, but about 60 RA-3′. The rtPCR results showed that only BV additional cases of pathogenic zoonotic BV infection genome was detected as positive (Cycle of threshold: have occurred sporadically and the fatality rate of 34) in the CSF specimen of the patient, while BV zoonotic BV infections is 70%–80%. Although the risk negative in other specimens from the patient and all for secondary transmission appears to be minimal, one specimens from close contacts; moreover, all tests were case of human-to-human transmission of herpes B negative for VZV, monkeypox virus, and virus has previously been documented (2). -

Chapter 29. Human Monkeypox and Other Poxvirus Infections of Man
CHAPTER 29 HUMAN MONKEYPOX AND OTHER POXVIRUS INFECTIONS OF MAN Contents Page Introduction 1287 Monkeypox in captive primates 1288 The properties of monkeypox virus 1290 Pathogenicity for laboratory animals 1290 Comparison of DNA maps of strains of monkeypox virus 1290 Genetic studies 1291 Species diagnosis 1292 Serological diagnosis of past monkeypox infection 1292 Human monkeypox 1292 Discovery of human infections 1292 Organization of laboratory research 1293 Organization of field research 1295 Incidence and distribution 1295 Clinical features 1297 Epidemiology 1303 Ecological studies 1308 Monkeypox : the overall picture 1311 Other Orthopoxvirus infections of man 1311 Vaccinia 1311 Cowpox 1312 Camelpox 1316 Parapoxvirus infections 1316 Molluscum contagiosum 1317 Tanapox virus infections 1318 General comment 1319 INTRODUCTION mild symptoms and usually only a localized skin lesion, the diseases in question presented Human monkeypox was first recognized in a potential diagnostic problem during the 1970 ; it is a severe systemic disease with a global eradication of smallpox, since virus generalized pustular rash, clinically indistin- particles found in lesions by electron micro- guishable from smallpox. In addition to va- scopic examination could be confused with riola and monkeypox viruses, 7 other species those of variola virus. Because of its import- of poxvirus, of 4 genera, can cause lesions in ance, monkeypox is the main subject of this man (Table 29 .1). Although infection with chapter, but a brief description is given of each of -

Monkeypox Fact Sheet
Monkeypox Fact Sheet What is monkeypox? Monkeypox is a rare disease caused by the monkeypox virus, which belongs to the same group of viruses as smallpox. Monkeypox virus was first found in laboratory monkeys in 1958. It has also been found in different kinds of rodents and primates in Africa. Who gets monkeypox? The first and only human cases of monkeypox in the United States occurred in the Midwest in 2003. Before 2003, the only human cases of monkeypox occurred in central and western parts of Africa. How is monkeypox spread? Monkeypox virus can spread to people when they are bitten by an animal infected with monkeypox or when they touch the blood, body fluids, or lesions of an infected animal. In the United States in 2003, monkeypox was reported among several people who had contact with sick pet prairie dogs that had contact with imported African rodents. Sometimes, monkeypox virus is spread from person to person through close contact or by touching body fluids of a person with monkeypox. In the United States in 2003, no one got sick from being in contact with another person with monkeypox. Objects, such as bedding or clothing, contaminated with the virus can also spread the monkeypox virus. What are the symptoms of monkeypox? In humans, the signs and symptoms of monkeypox are similar to those of smallpox, but they are usually milder. Monkeypox causes fever, headache, backache, swollen lymph nodes (not usually seen in smallpox), sore throat, and cough. One to three days after the onset of fever, a blister-like rash usually appears first on the face and then spreads to other parts of the body. -

Investigating Monkeypox in the Wild Recent Monkeypox Outbreak in Pet Prairie a Dogs Led to the first Recorded Human Case of the Disease in the U.S
Investigating Monkeypox in the Wild recent monkeypox outbreak in pet prairie A dogs led to the first recorded human case of the disease in the U.S. The outbreak has USGS scientists concerned the disease may spread to wild rodent populations. Monkeypox is a contagious orthopox Monkeypox Background virus related to smallpox. Its arrival in the U.S. from Africa in the Spring of Monkeypox is a disease native to Africa Most human monkeypox cases were traced back 2003 prompted the U.S. Geological that affects rodents such as squirrels to pet prairie dogs Survey (USGS) to launch a study to and mice, but other species are also determine if the disease infected wildlife susceptible, including a wide variety of and include swollen lymph nodes, populations. primates. The outbreak in 2003 marks fever, sore throat, chills, blisters, and the first time it was found in non-primate skin lesions. Animals suspected of USGS wildlife scientists became species in North America. being infected should be quarantined concerned the virus may have spread immediately and local health officials from infected pets or humans to wild Monkeypox is a zoonotic disease, should be contacted. animals. If monkeypox were to escape meaning humans can become infected into the wild, it could potentially find from an animal carrier. In Africa, The disease appears to have first come a reservoir in mice, squirrels, or other monkeypox is endemic, outbreaks occur to the U.S. through infected Gambian rodent populations. sporadically, and human-to-human giant rats from Africa that were housed transmission of the virus is documented.