Constructing Optimal IP Routing Tables
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
What Is Routing?
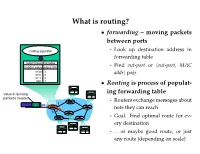
What is routing? • forwarding – moving packets between ports - Look up destination address in forwarding table - Find out-port or hout-port, MAC addri pair • Routing is process of populat- ing forwarding table - Routers exchange messages about nets they can reach - Goal: Find optimal route for ev- ery destination - . or maybe good route, or just any route (depending on scale) Routing algorithm properties • Static vs. dynamic - Static: routes change slowly over time - Dynamic: automatically adjust to quickly changing network conditions • Global vs. decentralized - Global: All routers have complete topology - Decentralized: Only know neighbors & what they tell you • Intra-domain vs. Inter-domain routing - Intra-: All routers under same administrative control - Intra-: Scale to ∼100 networks (e.g., campus like Stanford) - Inter-: Decentralized, scale to Internet Optimality A 6 1 3 2 F 1 E B 4 1 9 C D • View network as a graph • Assign cost to each edge - Can be based on latency, b/w, utilization, queue length, . • Problem: Find lowest cost path between two nodes - Must be computed in distributed way Distance Vector • Local routing algorithm • Each node maintains a set of triples - (Destination, Cost, NextHop) • Exchange updates w. directly connected neighbors - periodically (on the order of several seconds to minutes) - whenever table changes (called triggered update) • Each update is a list of pairs: - (Destination, Cost) • Update local table if receive a “better” route - smaller cost - from newly connected/available neighbor • Refresh existing -

Chapter 6: Chapter 6: Implementing a Border Gateway Protocol Solution Y
Chapter 6: Implementing a Border Gateway Protocol Solution for ISP Connectivity CCNP ROUTE: Implementing IP Routing ROUTE v6 Chapter 6 © 2007 – 2010, Cisco Systems, Inc. All rights reserved. Cisco Public 1 Chapter 6 Objectives . Describe basic BGP terminology and operation, including EBGP and IBGP. ( 3) . Configure basic BGP. (87) . Typical Issues with IBGP and EBGP (104) . Verify and troubleshoot basic BGP. (131) . Describe and configure various methods for manipulating path selection. (145) . Describe and configure various methods of filtering BGP routing updates. (191) Chapter 6 © 2007 – 2010, Cisco Systems, Inc. All rights reserved. Cisco Public 2 BGP Terminology, Concepts, and Operation Chapter 6 © 2007 – 2010, Cisco Systems, Inc. All rights reserved. Cisco Public 3 IGP versus EGP . Interior gateway protocol (IGP) • A routing protocol operating within an Autonomous System (AS). • RIP, OSPF, and EIGRP are IGPs. Exterior gateway protocol (EGP) • A routing protocol operating between different AS. • BGP is an interdomain routing protocol (IDRP) and is an EGP. Chapter 6 © 2007 – 2010, Cisco Systems, Inc. All rights reserved. Cisco Public 4 Autonomous Systems (AS) . An AS is a group of routers that share similar routing policies and operate within a single administrative domain. An AS typically belongs to one organization. • A singgpgyp()yle or multiple interior gateway protocols (IGP) may be used within the AS. • In either case, the outside world views the entire AS as a single entity. If an AS connects to the public Internet using an exterior gateway protocol such as BGP, then it must be assigned a unique AS number which is managed by the Internet Assigned Numbers Authority (IANA). -

The Routing Table V1.12 – Aaron Balchunas 1
The Routing Table v1.12 – Aaron Balchunas 1 - The Routing Table - Routing Table Basics Routing is the process of sending a packet of information from one network to another network. Thus, routes are usually based on the destination network, and not the destination host (host routes can exist, but are used only in rare circumstances). To route, routers build Routing Tables that contain the following: • The destination network and subnet mask • The “next hop” router to get to the destination network • Routing metrics and Administrative Distance The routing table is concerned with two types of protocols: • A routed protocol is a layer 3 protocol that applies logical addresses to devices and routes data between networks. Examples would be IP and IPX. • A routing protocol dynamically builds the network, topology, and next hop information in routing tables. Examples would be RIP, IGRP, OSPF, etc. To determine the best route to a destination, a router considers three elements (in this order): • Prefix-Length • Metric (within a routing protocol) • Administrative Distance (between separate routing protocols) Prefix-length is the number of bits used to identify the network, and is used to determine the most specific route. A longer prefix-length indicates a more specific route. For example, assume we are trying to reach a host address of 10.1.5.2/24. If we had routes to the following networks in the routing table: 10.1.5.0/24 10.0.0.0/8 The router will do a bit-by-bit comparison to find the most specific route (i.e., longest matching prefix). -

Understanding Linux Internetworking
White Paper by David Davis, ActualTech Media Understanding Linux Internetworking In this Paper Introduction Layer 2 vs. Layer 3 Internetworking................ 2 The Internet: the largest internetwork ever created. In fact, the Layer 2 Internetworking on term Internet (with a capital I) is just a shortened version of the Linux Systems ............................................... 3 term internetwork, which means multiple networks connected Bridging ......................................................... 3 together. Most companies create some form of internetwork when they connect their local-area network (LAN) to a wide area Spanning Tree ............................................... 4 network (WAN). For IP packets to be delivered from one Layer 3 Internetworking View on network to another network, IP routing is used — typically in Linux Systems ............................................... 5 conjunction with dynamic routing protocols such as OSPF or BGP. You c an e as i l y use Linux as an internetworking device and Neighbor Table .............................................. 5 connect hosts together on local networks and connect local IP Routing ..................................................... 6 networks together and to the Internet. Virtual LANs (VLANs) ..................................... 7 Here’s what you’ll learn in this paper: Overlay Networks with VXLAN ....................... 9 • The differences between layer 2 and layer 3 internetworking In Summary ................................................. 10 • How to configure IP routing and bridging in Linux Appendix A: The Basics of TCP/IP Addresses ....................................... 11 • How to configure advanced Linux internetworking, such as VLANs, VXLAN, and network packet filtering Appendix B: The OSI Model......................... 12 To create an internetwork, you need to understand layer 2 and layer 3 internetworking, MAC addresses, bridging, routing, ACLs, VLANs, and VXLAN. We’ve got a lot to cover, so let’s get started! Understanding Linux Internetworking 1 Layer 2 vs. -

Overview of Routing Security Landscape for the Quilt Member Meeting, Winter 2019 Mark Beadles, CISO, Oarnet [email protected] BGP IDLE
Overview of Routing Security Landscape for the Quilt Member Meeting, Winter 2019 Mark Beadles, CISO, OARnet [email protected] BGP IDLE CONNECT ACTIVE OPEN OPEN SENT CONFIRM ESTAB- LISHED 2/13/2019 Routing Security Landscape - The Quilt 2 Overview of Routing Security Landscape • Background • Threat environment • Current best practices • Gaps 2/13/2019 Routing Security Landscape - The Quilt 3 Background - Definitions • BGP • Border Gateway Protocol, an exterior path-vector gateway routing protocol • Autonomous System & Autonomous System Numbers • Collection of IP routing prefixes under control of a network operator on behalf of a single administrative domain that presents a defined routing policy to the Internet • Assigned number for each AS e.g. AS600 2/13/2019 Routing Security Landscape - The Quilt 4 Background - The BGP Security Problem By design, routers running BGP accept advertised routes from other BGP routers by default. (BGP was written under the assumption that no one would lie about the routes, so there’s no process for verifying the published announcements.) This allows for automatic and decentralized routing of traffic across the Internet, but it also leaves the Internet potentially vulnerable to accidental or malicious disruption, known as BGP hijacking. Due to the extent to which BGP is embedded in the core systems of the Internet, and the number of different networks operated by many different organizations which collectively make up the Internet, correcting this vulnerabilityis a technically and economically challenging problem. 2/13/2019 Routing Security Landscape - The Quilt 5 Background – BGP Terminology • Bogons • Objects (addresses/prefixes/ASNs) that don't belong on the internet • Spoofing • Lying about your address. -

P2P Resource Sharing in Wired/Wireless Mixed Networks 1
INT J COMPUT COMMUN, ISSN 1841-9836 Vol.7 (2012), No. 4 (November), pp. 696-708 P2P Resource Sharing in Wired/Wireless Mixed Networks J. Liao Jianwei Liao College of Computer and Information Science Southwest University of China 400715, Beibei, Chongqing, China E-mail: [email protected] Abstract: This paper presents a new routing protocol called Manager-based Routing Protocol (MBRP) for sharing resources in wired/wireless mixed networks. MBRP specifies a manager node for a designated sub-network (called as a group), in which all nodes have the similar connection properties; then all manager nodes are employed to construct the backbone overlay network with ring topology. The manager nodes act as the proxies between the internal nodes in the group and the external world, that is not only for centralized management of all nodes to a certain extent, but also for avoiding the messages flooding in the whole network. The experimental results show that compared with Gnutella2, which uses super-peers to perform similar management work, the proposed MBRP has less lookup overhead including lookup latency and lookup hop count in the most of cases. Besides, the experiments also indicate that MBRP has well configurability and good scaling properties. In a word, MBRP has less transmission cost of the shared file data, and the latency for locating the sharing resources can be reduced to a great extent in the wired/wireless mixed networks. Keywords: wired/wireless mixed network, resource sharing, manager-based routing protocol, backbone overlay network, peer-to-peer. 1 Introduction Peer-to-Peer technology (P2P) is a widely used network technology, the typical P2P network relies on the computing power and bandwidth of all participant nodes, rather than a few gathered and dedicated servers for central coordination [1, 2]. -

Chapter 12, “Configuring Layer 3 Interfaces”
CHAPTER 12 Configuring Layer 3 Interfaces This chapter contains information about how to configure Layer 3 interfaces on the Catalyst 6500 series switches, which supplements the information and procedures in the Release 12.1 publications at this URL: http://www.cisco.com/univercd/cc/td/doc/product/software/ios121/121cgcr/index.htm This chapter consists of these sections: • Configuring IP Routing and Addresses, page 12-2 • Configuring IPX Routing and Network Numbers, page 12-6 • Configuring AppleTalk Routing, Cable Ranges, and Zones, page 12-7 • Configuring Other Protocols on Layer 3 Interfaces, page 12-8 Catalyst 6500 Series Switch Cisco IOS Software Configuration Guide—Release 12.1 E 78-14099-04 12-1 Chapter 12 Configuring Layer 3 Interfaces Configuring IP Routing and Addresses Note • For complete syntax and usage information for the commands used in this chapter, refer to the Catalyst 6500 Series Switch Cisco IOS Command Reference publication and the Release 12.1 publications at this URL: http://www.cisco.com/univercd/cc/td/doc/product/software/ios121/121cgcr/index.htm • Release 12.1(13)E and later releases support configuration of 4,096 Layer 3 VLAN interfaces. – We recommend that you configure a combined total of no more than 2,000 Layer 3 VLAN interfaces and Layer 3 ports on an MSFC2 with either Supervisor Engine 1 or Supervisor Engine 2. – We recommend that you configure a combined total of no more than 1,000 Layer 3 VLAN interfaces and Layer 3 ports on an MSFC. • With releases earlier than Release 12.1(13)E, an MSFC2 with either Supervisor Engine 1 or Supervisor Engine 2 supports a combined maximum of 1,000 Layer 3 VLAN interfaces and Layer 3 ports. -

Lab 5.5.2: Examining a Route
Lab 5.5.2: Examining a Route Topology Diagram Addressing Table Device Interface IP Address Subnet Mask Default Gateway S0/0/0 10.10.10.6 255.255.255.252 N/A R1-ISP Fa0/0 192.168.254.253 255.255.255.0 N/A S0/0/0 10.10.10.5 255.255.255.252 10.10.10.6 R2-Central Fa0/0 172.16.255.254 255.255.0.0 N/A N/A 192.168.254.254 255.255.255.0 192.168.254.253 Eagle Server N/A 172.31.24.254 255.255.255.0 N/A host Pod# A N/A 172.16. Pod#.1 255.255.0.0 172.16.255.254 host Pod# B N/A 172.16. Pod#. 2 255.255.0.0 172.16.255.254 S1-Central N/A 172.16.254.1 255.255.0.0 172.16.255.254 All contents are Copyright © 1992–2007 Cisco Systems, Inc. All rights reserved. This document is Cisco Public Information. Page 1 of 7 CCNA Exploration Network Fundamentals: OSI Network Layer Lab 5.5.1: Examining a Route Learning Objectives Upon completion of this lab, you will be able to: • Use the route command to modify a Windows computer routing table. • Use a Windows Telnet client command telnet to connect to a Cisco router. • Examine router routes using basic Cisco IOS commands. Background For packets to travel across a network, a device must know the route to the destination network. This lab will compare how routes are used in Windows computers and the Cisco router. -

Routing Tables
Routing Tables A routing table is a grouping of information stored on a networked computer or network router that includes a list of routes to various network destinations. The data is normally stored in a database table and in more advanced configurations includes performance metrics associated with the routes stored in the table. Additional information stored in the table will include the network topology closest to the router. Although a routing table is routinely updated by network routing protocols, static entries can be made through manual action on the part of a network administrator. How Does a Routing Table Work? Routing tables work similar to how the post office delivers mail. When a network node on the Internet or a local network needs to send information to another node, it first requires a general idea of where to send the information. If the destination node or address is not connected directly to the network node, then the information has to be sent via other network nodes. In order to save resources, most local area network nodes will not maintain a complex routing table. Instead, they will send IP packets of information to a local network gateway. The gateway maintains the primary routing table for the network and will send the data packet to the desired location. In order to maintain a record of how to route information, the gateway will use a routing table that keeps track of the appropriate destination for outgoing data packets. All routing tables maintain routing table lists for the reachable destinations from the router’s location. -

TCP/IP Protocol Suite
TCP/IP Protocol Suite Marshal Miller Chris Chase Robert W. Taylor (Director of Information Processing Techniques Office at ARPA 1965-1969) "For each of these three terminals, I had three different sets of user commands. So if I was talking online with someone at S.D.C. and I wanted to talk to someone I knew at Berkeley or M.I.T. about this, I had to get up from the S.D.C. terminal, go over and log into the other terminal and get in touch with them. I said, oh, man, it's obvious what to do: If you have these three terminals, there ought to be one terminal that goes anywhere you want to go where you have interactive computing. That idea is the ARPANET." – New York Times Interview: December 20, 1999 Overview • Terminology • History • Technical Details: – TCP – IP – Related Protocols • Physical Media • Social Implications • Economic Impact 3 Terminology • Protocol – A set of rules outlining the format to be used for communication between systems • Domain Name System (DNS) – Converts an Internet domain into an IP address • Router – A computer or software package used in packet switched networks to look at the source and destination addresses, and decide where to send the packets • Uniform Resource Indicators – Uniform Resource Location (URL) • How to find the resource: HTTP, FTP, Telnet – Uniform Resource Names (URN) • What the resource is: Not as common as URL 4 History: Pre-TCP/IP • Networks existed and information could be transferred within • Because of differences in network implementation communication between networks different for each application • Need for unification in protocols connecting networks 5 History: TCP/IP Development • 1968: Plans develop for using Interface Message Processors (IMPs) • Dec. -

Introduction to the Border Gateway Protocol – Case Study Using GNS3
Introduction to The Border Gateway Protocol – Case Study using GNS3 Sreenivasan Narasimhan1, Haniph Latchman2 Department of Electrical and Computer Engineering University of Florida, Gainesville, USA [email protected], [email protected] Abstract – As the internet evolves to become a vital resource for many organizations, configuring The Border Gateway protocol (BGP) as an exterior gateway protocol in order to connect to the Internet Service Providers (ISP) is crucial. The BGP system exchanges network reachability information with other BGP peers from which Autonomous System-level policy decisions can be made. Hence, BGP can also be described as Inter-Domain Routing (Inter-Autonomous System) Protocol. It guarantees loop-free exchange of information between BGP peers. Enterprises need to connect to two or more ISPs in order to provide redundancy as well as to improve efficiency. This is called Multihoming and is an important feature provided by BGP. In this way, organizations do not have to be constrained by the routing policy decisions of a particular ISP. BGP, unlike many of the other routing protocols is not used to learn about routes but to provide greater flow control between competitive Autonomous Systems. In this paper, we present a study on BGP, use a network simulator to configure BGP and implement its route-manipulation techniques. Index Terms – Border Gateway Protocol (BGP), Internet Service Provider (ISP), Autonomous System, Multihoming, GNS3. 1. INTRODUCTION Figure 1. Internet using BGP [2]. Routing protocols are broadly classified into two types – Link State In the figure, AS 65500 learns about the route 172.18.0.0/16 through routing (LSR) protocol and Distance Vector (DV) routing protocol. -

The Routing Table Lookup Process
The Routing Table Part 2 – The Routing Table Lookup Process By Rick Graziani Cisco Networking Academy [email protected] Updated: Oct. 10, 2002 This document is the second of two parts dealing with the routing table. Part I discussed the structure of the routing table, and how routes are created. Part II will discuss how the routing table lookup process finds the “best” route within the routing table. What happens when a router receives an IP packet, examines the IP destination address and looks that address up in the routing table? How does the router decide which route in the routing table is the best match? What affect does the subnet mask have on the routing table? How does the router decide whether or not to use a supernet or default route if there is not a better match? We will answer these questions and more in this document. The network we will be using is a simple three router network. RouterA and Router B share the common major network 172.16.0.0/24. RouterB and RouterC are connected by the 192.168.1.0/24 network. You will notice that RouterC also has a 172.16.4.0/24 subnet which is disconnected, or discontiguous, from the rest of the 172.16.0.0 network. 172.16.1.0/24 172.16.3.0/24 172.16.4.0/24 .1 fa0 .1 fa0 .1 fa0 .1 172.16.2.0/24 .2 .1 192.168.1.0/24 .2 s0 s0 s1 s0 Router A Router B Router C Most of this information is best explained by using examples.