Physical Chemistry
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
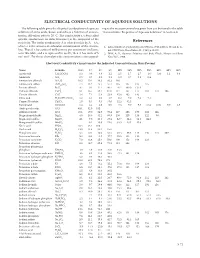
CRC Handbook of Chemistry and Physics, 91Th Edition
ELECTRICAL CONDUCTIVITY OF AQUEOUS SOLUTIONS The following table gives the electrical conductivity of aqueous ing to the mass percent values given here can be found in the table solutions of some acids, bases, and salts as a function of concen- “Concentrative Properties of Aqueous Solutions” in Section 8 . tration . All values refer to 20 °C . The conductivity κ (often called specific conductance in older literature) is the reciprocal of the resistivity . The molar conductivity Λ is related to this by Λ = κ/c, References where c is the amount-of-substance concentration of the electro- 1 . CRC Handbook of Chemistry, and Physics, 70th Edition, Weast, R . C ., lyte . Thus if κ has units of millisiemens per centimeter (mS/cm), Ed ., CRC Press, Boca Raton, FL, 1989, p . D-221 . as in this table, and c is expressed in mol/L, then Λ has units of S 2 . Wolf, A . V ., Aqueous Solutions and Body Fluids, Harper and Row, cm2 mol-1 . For these electrolytes the concentration c correspond- New York, 1966 . Electrical Conductivity κ in mS/cm for the Indicated Concentration in Mass Percent Name Formula 0.5% 1% 2% 5% 10% 15% 20% 25% 30% 40% 50% Acetic acid CH3COOH 0 .3 0 .6 0 .8 1 .2 1 .5 1 .7 1 .7 1 .6 1 .4 1 .1 0 .8 Ammonia NH3 0 .5 0 .7 1 .0 1 .1 1 .0 0 .7 0 .5 0 .4 Ammonium chloride NH4Cl 10 .5 20 .4 40 .3 95 .3 180 Ammonium sulfate (NH4)2SO4 7 .4 14 .2 25 .7 57 .4 105 147 185 215 Barium chloride BaCl2 4 .7 9 .1 17 .4 40 .4 76 .7 109 .0 137 .0 Calcium chloride CaCl2 8 .1 15 .7 29 .4 67 .0 117 157 177 183 172 106 Cesium chloride CsCl 3 .8 7 .4 13 .8 -

Ion Pair Conductivity Model and Its Application for Predicting Conductivity in Non-Polar Systems
Ion Pair Conductivity Model and Its Application for Predicting Conductivity in Non-Polar Systems Sean Parlia Submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy under the Executive Committee of the Graduate School of Arts and Sciences COLUMBIA UNIVERSITY 2020 © 2020 Sean Parlia All Rights Reserved ABSTRACT Ion-Pair Conductivity Model and Its Application for Predicting Conductivity in Non-Polar Systems By Sean Parlia While the laws of ionization and conductivity in polar systems are well understood and appreciated in the art, theories related to nonpolar systems and their conductivities remain elusive. Currently, multiple conflicting models, with limited experimental verification, exist that aim to explain and predict the mechanisms by which ionization occurs in nonpolar media. A historical overview of the field of nonpolar electrochemistry, dating back to the 1800’s, is presented herein with a focus on the work of prominent scientists such as Fuoss, Bjerrum, and Onsager, who’s pioneering discoveries serve as the scientific foundation for our understanding of ionization in nonpolar systems, from which our knowledge of ion-pairs (i.e. re-associated solvated ions which do not contribute to the overall conductivity of the system) stems. Recent work in the field of nonpolar electrochemistry has focused on ionization models such as the Disproportionation Model and the Fluctuation Model, which ignore ion-pair formation and the existence of these neutral entities altogether. While, the “Ion-Pair Conductivity Model”, the novel conductivity model introduced and explored herein, primarily focuses on the critical role these neutral entities play with regards to the electrochemistry in these systems. -

Electrochemistry Galvenic Cell Or Voltoic Cell 1. Identify the Location of Oxidation in an Electrochemical Cell. A) the Anode B)
Electrochemistry Galvenic cell or voltoic cell 1. Identify the location of oxidation in an electrochemical cell. a) the anode b) the cathode c) the electrode d) the salt bridge 2. Which one of the following is not a function of a salt bridge? a) To allow the flow of cations from one solution to the other b) To allow the flow of anions from one solution to the other c) To allow the electrons to flow from one solution to the other d) To maintain electrical neutrality of the two solutions. 3. If the salt bridge is removed suddenly from a working cell, the voltage a) Increases b) decreases c) Drops to zero d) May increase or decrease depending upon cell reaction 4. A cell is formed by the combination of a standard Mg electrode and a standard Zn electrode. Their reduction potentials are respectively –2.36V and ‐ 0.76V. The emf of the cell is a) +1.6V b) –1.6V b) +3.12V d) none of these 5. Copper has less SRP than silver (placed above silver in the electrochemical series). So if a copper electrode is combined with a silver electrode to form a cell, then the cell operates. a) Copper is oxidised b) silver is oxidized c) Silver gains electrons d) silver loses electrons. 6. The reduction potentials of three elements A, B and C are –2.37V, ‐0.76V, and +0V respectively. Then from the aqueous solution. a) C displaces hydrogen b) C is bases than A & B c) A displaces B but not C d) A displaces B and C. -

Molar Conductivities of Aqueous Electrolytes
Laboratory Manual, Physical Chemistry, Year 1 Experiment 5 ___________________________________________________________________________________ EXPERIMENT 5 MOLAR CONDUCTIVITIES OF AQUEOUS ELECTROLYTES Objective: To determine the conductivity of various acid and the dissociation constant, Ka for acetic acid 1 Theory 1.1 Electrical conductivity in solutions An electric current in solution is the result of the net movement of free ions in a specific direction. The current may be determined by measuring the resistance R between two similar inert electrodes immersed in the solution, as in the figure below where the oval region represents the solution; A represents the electrode area and l is the normal distance between the electrode planes. In actual practice an A.C. current with a low frequency of the order of approximately 1000 Hertz is used (to prevent electrolysis) in the measurement, and the components representing the resistance R in the complex impedance Z for the circuit is determined. We will always refer to this component (the real portion of the complex impedance) for what follows. The resistance is also dependent on the frequency (Debye-Falkenhagen effect). The theory and measurement here concentrates on low frequency measurements where the Onsager equation is meaningful. The fully automated measuring apparatus has been configured for low frequency measurement in accordance with the theory of electrolytes. Electrod e l l =Distance between electrode A = Area of A electrode Figure of conductivity circuit According to Ohm’s law, the resistance R (unit Ohm, symbol Ω ) for the above circuit l is given by R = ρ (1) A l where ρ is the resistivity of the solution. -

Copper (II) Selenite
Sparingly Soluble Selenites 377 COMPONENTS: ORIGINAL MEASUREMENTS: 1. Copper(II) selenIte; CuSe03; Ripan, R.; Verlceanu, G. [10214-40-1] StudJa UnIV. Babes-Bo1yal, Serf Chlm. 2. Water; H20; [7732-18-5] 1968, 13, 31-37. VARIABLES: PREPARED BY: One temperature: 291 K Mary R. Masson EXPERIMENTAL VALUES: All concentratIons are expressed in unIts of mol dm- 3 • ConcentratIon KsO Mean KsO pKsO mol 2 dm-6 1. 747 x 10-4 2.9 x 1O-~ 3.2 ± 0.4 x 10-8 7.49 1.741 x 10-4 3.1 x 10- 1.855 x 10-4 3.4 x 10-8 mol 2 dm-6 1.848 x 10-4 3.4 x 10-8 1.820 x 10-4 3.3 x 10-8 1.880 x 10-4 3.4 x 10-8 The concentration c in the saturated solution was calculated from the measured conductivity K from the equatIon 1000K c = ---xrr ComplIer's note Neither in the determinatIon of the Ionic conductivIty of the selenite ion nor in the evaluatIon of the solubilIty product was hydrolysis of the selenIte ion taken Into acco~~t. This would give_rise to errors, since~ for example, in a O.OOlM solutIon, [Se03 ] = 0.000955M, [HSe03] = 0.000045M and [OH ] = 0.000045M, and hydroxide and hydrogen selenIte have dIfferent ionic conductivIties from selenite. If the ionIC conductivity of hydrogen selenIte were known, the experImental results could have been interpreted correctly (cf. ref. 2), but thIS value does not seem to be avaIlable. However, because the calibratIon and sample SolutIons had concentrations of about the same order of magnItude, the errors would cancel to some extent, but the KsO value cannot be regarded as reliable. -
C:\Documents and Settings\Schurko\My Documents
EXPERIMENT 2 DETERMINATION OF Ka USING THE CONDUCTANCE METHOD Introduction Equilibrium Processes When a pure sample of liquid-state acetic acid (i.e., CH3COOH(l)/HAc(l)) is added to a beaker of pure water, at least two significant processes occur. First, the acetic acid (assuming it to be the solute) will dissolve completely in the water (assuming it to be the solvent). As acetic acid is infinitely soluble in water (i.e., the two liquids are miscible), this process of dissolution will result in a solution of acetic acid and water with no measurable amount of pure solute. As this process has proceeded completely, (i.e., 100 %) an equilibrium expression need not be considered. Second, the dissolved acetic acid will undergo the process of dissociation, a process which may be represented by an equilibrium expression and which is the focus of this lab. Both processes may be expressed symbolically: H2O(l) - + CH3COOH(l) CH3COOH(aq) CH3COO (aq) H (aq) When acetic acid dissociates, a proton is liberated, and therefore the equilibrium constant representing this process is referred to as the acid dissociation constant (Ka). +− γ +−γ []HCHCOO[]3 ()(HCHCOO ) K =×3 [1] a γ []CH3 COOH (CH3COOH) where the parameter γ is defined as the activity coefficient of that particular substance. Conductance A very common method to use when determining the acid dissociation constant of a sample is called the conductance method, as one measures the conductance of a solution. Conductance, G, (SI unit is the seimens, S, where 1 S / 1 Ω-1) is defined as the reciprocal of resistance and can be understood to represent the ease with which electrical current flows through a given substance. -

Electrolyte and Dissociation
Seminar 4 Conductivity and Conductometry. Electrolyte properties. Electricity flow through the electrolyte. Conductivity of electrolyte solutions (specific, molar) and its dependence on concentration. Determination of the limiting molar conductivity. Kohlrausch’s law. The use of electrolyte conductivity for physicochemical calculations (dissociation constant and degree, solubility product). Examples of conductometric titration (conductometry). Examples of graphs, tasks and their solutions. Tomasz Tuzimski Medical University of Lublin, Faculty of Pharmacy with Medical Analytics Division, Chair of Chemistry, Department of Physical Chemistry, 4A Chodźki Street, 20-093 Lublin, Poland E-mail: [email protected] Electrolyte and Dissociation An electrolyte is a substance that, when molten or dissolved in a solvent, breaks down into free ions (dissociates) as a result of which it can conduct electricity. Their ability to conduct electricity suggests the presence of electrically charged particles that are able to move through the solution. The generally accepted reason is that when an ionic compound dissolved in water, the ions separate from each other and enter the solution as more or less independent particles that are surrounded by molecules of the solvent. The change is called the dissociation of the ionic compounds. Dissociation of an ionic compound as it disolves in water. Ions separate from the solid and become surrounded by the molecules of water. The ions are said to be hydrated. Equations for dissociation reactions show the ions Acid dissociation constant Ka An acid ionization constant = An acid dissociation constant Base dissociation constant Kb Base ionization constant = Base dissociation constant Remember: you can't use the dissociation constant formula for strong electrolytes! Dissociation degree α Studies on electrolytes have shown that, despite the same molar concentration of different electrolytes in solution, they differ in their ability to conduct electricity. -

Experiment 6 - Conductance of Electrolytes
1 EXPERIMENT 6 - CONDUCTANCE OF ELECTROLYTES THEORY We all know that the solutions of electrolytes conduct an electric current by the motion of the cations towards the cathode, and anions towards the anode. Metallic conductors are known to obey Ohm’s Law: ΔΦ I = (1) R where I is the current in amperes, ΔΦ is the difference in the electric potential between the terminals of the conductor in volts, and R is the resistance in ohms. R depends upon the dimensions of the conductor: l R ρ= (2) A where l is length, A is the cross-sectional area and ρ is the special resistance, i.e. resistivity, in Ωm. Reciprocal resistance, 1/R, is known as conductance, and reciprocal resistivity, 1/ρ, as conductivity. Conductivity is given by the symbol kappa,κ and has units Ω-1m-1 or Sm-1 (S = Ω-1). Hence, l κ = (3) RA Conductivity depends upon the number of charge carriers (i.e. ions) present in the solution. It is therefore, reasonable to express it in terms of molar conductivity:Λm Λ = κ (4) m c where c is the molar concentration of the electrolyte. We can classify electrolytes as a) strong electrolytes, and b) weak electrolytes. The strong electrolytes have high molar conductivities, and their conductivities change very little if the solution is diluted down. In the case of weak electrolytes, however, there is little conductivity in concentrated solutions.The conductivity increases upon increasing dilution. The value of Λm extrapolated to zero concentration (i.e. theoretical infinite dilution) is known as Λm0, the molar conductivity at infinite dilution when ion interaction is assumed to be zero. -

Molar Conductivity at a Concentration of 1 Mol/Cm3 Or the Equivalent Conductivity at the Concentration of Gram-Equivalent/Cm3 Is Chosen for This Purpose
Institute of Metallurgy and Materials Science Polish Academy of Sciences Electrochemistry for materials science Ewa Bełtowska-Lehman Institute of Metallurgy and Materials Science Polish Academy of Sciences ELECTROCHEMISTRY FOR MATERIALS SCIENCE Ewa Bełtowska-Lehman Electrochemistry for materials science PART II PROPERTIES OF AQUEOUS SOLUTION OF ELECTROLYTES Ewa Bełtowska-Lehman PROPERTIES OF AQUEOUS SOLUTIONS In the electrochemical technology, a plating bath (i.e. the aqueous solutions of salts of various metals) plays a key role. PLATING BATH = ELECTROPLATING BATH = ELECTROLYTIC BATH = GALVANIC BATH = ELECTROLYTE SOLUTION TERMS SOLUTION: homogeneous mixture of two or more substances SOLUTE: substance present in smaller amount SOLVENT: substance present in greater amount AQUEOUS SOLUTION: solvent is water EELCTROLYTE: any substance containing free ions that behaves as an electrically conductive medium Substances behave differently when they are placed in water, specifically ionic versus covalent compounds. One breaks apart in water, the other does not. Electrolytes are ionic and strong acid solutions. Nonelectrolytes are covalent compounds. Weak electrolytes are in between. ELECTROLYTIC PROPERTIES (STRONG, WEAK AND NONELECTROLYTES) HClO3 H2SO4 HNO3 HF STRONG ELECTROLYTE: substance that, when dissolved in water, can conduct electricity (e.g. HCl, HBr, HJ, HClO4, HNO3, H2SO4, NaOH, KOH, LiOH, Ba(OH)2 , Ca(OH)2, NaCl, KBr, MgCl2 and other) HNO3 > H2SO4 acid strength HCl, HBr, HJ acid strength HClO , HBrO , HJO 3 3 3 basic strength HClO4 > HClO3 > HClO2 > HClO ELECTROLYTIC PROPERTIES (STRONG, WEAK AND NONELECTROLYTES) WEAK ELECTROLYTE: substance that is a poor conductor of electricity when dissolved in water (e.g. H2S, H2SO3, HNO2, HF, CH3COOH acetic acid, H2CO3 carbonic acid, H3PO4 phosphoric acid, Cu(OH)2, NH4OH, all containing "N" and other) NONELECTROLYTE: substance that does not conduct electricity when dissolved in water (e.g. -

Jo-2015-008303 Micelle Formation in Liquid Ammonia
Supporting Information The Journal of Organic Chemistry Manuscript ID: jo-2015-008303 Micelle Formation in Liquid Ammonia Joseph M. Griffin, John H. Atherton and Michael I. Page* IPOS, The Page Laboratories, Department of Chemical and Biological Sciences, The University of Huddersfield, Queensgate, Huddersfield, HD1 3DH, United Kingdom Contents Page 1. Ostwald’s dilution law for weak electrolytes 2 2. Kohlrausch’s law for strong electrolytes 4 3. Observed pseudo-first-order rate constants for the ammonolysis of propargyl benzoate as a function of perfluorononanamide concentration 6 1 1. Ostwald’s dilution law for weak electrolytes: Attempts were made to fit the liquid ammonia data to Ostwald’s dilution law: 1 1 ΛΛc = ∘ + ∘ ͦ ΛΛ ΛΛ ͅΏ(ΛΛ) Where: ͦ ͯͥ ΛΛ = Molar conductivity (Sm mol ) ∘ ͦ ͯͥ ΛΛ = Molar conductivity at infinite dilution (Sm mol ) ͅΏ = Acid dissociation constant c = Concentration of electrolyte (M) In water a plot cΛm against 1/Λm gives a straight line for a weak electrolyte such as acetic acid: 1.0E-04 8.0E-05 -3 6.0E-05 dm 2 Sm 4.0E-05 m Λ c 2.0E-05 0.0E+00 0 1000 2000 3000 1/Λ (mol S -1 m-2) m 2 But for liquid ammonia, this relationship is not observed for a simple salt, NH 4Cl, and ionic surfactants: NH 4Cl in liquid ammonia: 5.0E-04 4.0E-04 -3 3.0E-04 dm 2 Sm m m 2.0E-04 Λ c 1.0E-04 0.0E+00 0 50 100 150 200 250 1/Λ (mol S -1 m-2) m Perfluorooctanoic acid in liquid ammonia: 3.0E-04 2.5E-04 -3 2.0E-04 dm 2 1.5E-04 Sm m m Λ c 1.0E-04 5.0E-05 0.0E+00 0 20 40 60 80 100 120 140 -1 -2 1/Λ m (mol S m ) 3 2.