Synthesizing Realistic Facial Expressions from Photographs Z
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

3D Visualization of Weather Radar Data Examensarbete Utfört I Datorgrafik Av
3D Visualization of Weather Radar Data Examensarbete utfört i datorgrafik av Aron Ernvik lith-isy-ex-3252-2002 januari 2002 3D Visualization of Weather Radar Data Thesis project in computer graphics at Linköping University by Aron Ernvik lith-isy-ex-3252-2002 Examiner: Ingemar Ragnemalm Linköping, January 2002 Avdelning, Institution Datum Division, Department Date 2002-01-15 Institutionen för Systemteknik 581 83 LINKÖPING Språk Rapporttyp ISBN Language Report category Svenska/Swedish Licentiatavhandling ISRN LITH-ISY-EX-3252-2002 X Engelska/English X Examensarbete C-uppsats Serietitel och serienummer ISSN D-uppsats Title of series, numbering Övrig rapport ____ URL för elektronisk version http://www.ep.liu.se/exjobb/isy/2002/3252/ Titel Tredimensionell visualisering av väderradardata Title 3D visualization of weather radar data Författare Aron Ernvik Author Sammanfattning Abstract There are 12 weather radars operated jointly by SMHI and the Swedish Armed Forces in Sweden. Data from them are used for short term forecasting and analysis. The traditional way of viewing data from the radars is in 2D images, even though 3D polar volumes are delivered from the radars. The purpose of this work is to develop an application for 3D viewing of weather radar data. There are basically three approaches to visualization of volumetric data, such as radar data: slicing with cross-sectional planes, surface extraction, and volume rendering. The application developed during this project supports variations on all three approaches. Different objects, e.g. horizontal and vertical planes, isosurfaces, or volume rendering objects, can be added to a 3D scene and viewed simultaneously from any angle. Parameters of the objects can be set using a graphical user interface and a few different plots can be generated. -

Opengl 4.0 Shading Language Cookbook
OpenGL 4.0 Shading Language Cookbook Over 60 highly focused, practical recipes to maximize your use of the OpenGL Shading Language David Wolff BIRMINGHAM - MUMBAI OpenGL 4.0 Shading Language Cookbook Copyright © 2011 Packt Publishing All rights reserved. No part of this book may be reproduced, stored in a retrieval system, or transmitted in any form or by any means, without the prior written permission of the publisher, except in the case of brief quotations embedded in critical articles or reviews. Every effort has been made in the preparation of this book to ensure the accuracy of the information presented. However, the information contained in this book is sold without warranty, either express or implied. Neither the author, nor Packt Publishing, and its dealers and distributors will be held liable for any damages caused or alleged to be caused directly or indirectly by this book. Packt Publishing has endeavored to provide trademark information about all of the companies and products mentioned in this book by the appropriate use of capitals. However, Packt Publishing cannot guarantee the accuracy of this information. First published: July 2011 Production Reference: 1180711 Published by Packt Publishing Ltd. 32 Lincoln Road Olton Birmingham, B27 6PA, UK. ISBN 978-1-849514-76-7 www.packtpub.com Cover Image by Fillipo ([email protected]) Credits Author Project Coordinator David Wolff Srimoyee Ghoshal Reviewers Proofreader Martin Christen Bernadette Watkins Nicolas Delalondre Indexer Markus Pabst Hemangini Bari Brandon Whitley Graphics Acquisition Editor Nilesh Mohite Usha Iyer Valentina J. D’silva Development Editor Production Coordinators Chris Rodrigues Kruthika Bangera Technical Editors Adline Swetha Jesuthas Kavita Iyer Cover Work Azharuddin Sheikh Kruthika Bangera Copy Editor Neha Shetty About the Author David Wolff is an associate professor in the Computer Science and Computer Engineering Department at Pacific Lutheran University (PLU). -

Phong Shading
Computer Graphics Shading Based on slides by Dianna Xu, Bryn Mawr College Image Synthesis and Shading Perception of 3D Objects • Displays almost always 2 dimensional. • Depth cues needed to restore the third dimension. • Need to portray planar, curved, textured, translucent, etc. surfaces. • Model light and shadow. Depth Cues Eliminate hidden parts (lines or surfaces) Front? “Wire-frame” Back? Convex? “Opaque Object” Concave? Why we need shading • Suppose we build a model of a sphere using many polygons and color it with glColor. We get something like • But we want Shading implies Curvature Shading Motivation • Originated in trying to give polygonal models the appearance of smooth curvature. • Numerous shading models – Quick and dirty – Physics-based – Specific techniques for particular effects – Non-photorealistic techniques (pen and ink, brushes, etching) Shading • Why does the image of a real sphere look like • Light-material interactions cause each point to have a different color or shade • Need to consider – Light sources – Material properties – Location of viewer – Surface orientation Wireframe: Color, no Substance Substance but no Surfaces Why the Surface Normal is Important Scattering • Light strikes A – Some scattered – Some absorbed • Some of scattered light strikes B – Some scattered – Some absorbed • Some of this scattered light strikes A and so on Rendering Equation • The infinite scattering and absorption of light can be described by the rendering equation – Cannot be solved in general – Ray tracing is a special case for -
Scan Conversion & Shading
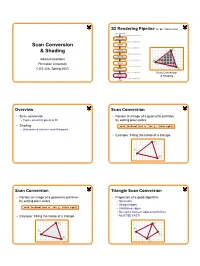
3D Rendering Pipeline (for direct illumination) 3D Primitives 3D Modeling Coordinates Modeling TransformationTransformation 3D World Coordinates Scan Conversion LightingLighting 3D World Coordinates ViewingViewing P1 & Shading TransformationTransformation 3D Camera Coordinates ProjectionProjection TransformationTransformation Adam Finkelstein 2D Screen Coordinates P2 Princeton University Clipping 2D Screen Coordinates ViewportViewport COS 426, Spring 2003 TransformationTransformation P3 2D Image Coordinates Scan Conversion ScanScan Conversion & Shading 2D Image Coordinates Image Overview Scan Conversion • Scan conversion • Render an image of a geometric primitive o Figure out which pixels to fill by setting pixel colors • Shading void SetPixel(int x, int y, Color rgba) o Determine a color for each filled pixel • Example: Filling the inside of a triangle P1 P2 P3 Scan Conversion Triangle Scan Conversion • Render an image of a geometric primitive • Properties of a good algorithm by setting pixel colors o Symmetric o Straight edges void SetPixel(int x, int y, Color rgba) o Antialiased edges o No cracks between adjacent primitives • Example: Filling the inside of a triangle o MUST BE FAST! P1 P1 P2 P2 P4 P3 P3 1 Triangle Scan Conversion Simple Algorithm • Properties of a good algorithm • Color all pixels inside triangle Symmetric o void ScanTriangle(Triangle T, Color rgba){ o Straight edges for each pixel P at (x,y){ Antialiased edges if (Inside(T, P)) o SetPixel(x, y, rgba); o No cracks between adjacent primitives } } o MUST BE FAST! P P1 -

Evaluation of Image Quality Using Neural Networks
R. CANT et al: EVALUATION OF IMAGE QUALITY EVALUATION OF IMAGE QUALITY USING NEURAL NETWORKS R.J. CANT AND A.R. COOK Simulation and Modelling Group, Department of Computing, The Nottingham Trent University, Burton Street, Nottingham NG1 4BU, UK. Tel: +44-115-848 2613. Fax: +44-115-9486518. E-mail: [email protected]. ABSTRACT correspondence between human and neural network seems to depend on the level of expertise of the human subject. We discuss the use of neural networks as an evaluation tool for the graphical algorithms to be used in training simulator visual systems. The neural network used is of a type developed by the authors and is The results of a number of trial evaluation studies are presented in described in detail in [Cant and Cook, 1995]. It is a three-layer, feed- summary form, including the ‘calibration’ exercises that have been forward network customised to allow both unsupervised competitive performed using human subjects. learning and supervised back-propagation training. It has been found that in some cases the results of competitive learning alone show a INTRODUCTION better correspondence with human performance than those of back- propagation. The problem here is that the back-propagation results are too good. Training simulators, such as those employed in vehicle and aircraft simulation, have been used for an ever-widening range of applications The following areas of investigation are presented here: resolution and in recent years. Visual displays form a major part of virtually all of sampling, shading algorithms, texture anti-aliasing techniques, and these systems, most of which are used to simulate normal optical views, model complexity. -

Cutting Planes and Beyond 1 Abstract 2 Introduction
Cutting Planes and Beyond Michael Clifton and Alex Pang Computer Information Sciences Board University of California Santa Cruz CA Abstract We present extensions to the traditional cutting plane that b ecome practical with the availability of virtual reality devices These extensions take advantage of the intuitive ease of use asso ciated with the cutting metaphor Using their hands as the cutting to ol users interact directly with the data to generate arbitrarily oriented planar surfaces linear surfaces and curved surfaces We nd that this typ e of interaction is particularly suited for exploratory scientic visualization where features need to b e quickly identied and precise p ositioning is not required We also do cument our investigation on other intuitive metaphors for use with scientic visualization Keywords curves cutting planes exploratory visualization scientic visualization direct manipulation Intro duction As a visualization to ol virtual reality has shown promise in giving users a less inhibited metho d of observing and interacting with data By placing users in the same environment as the data a b etter sense of shap e motion and spatial relationship can b e conveyed Instead of a static view users are able to determine what they see by navigating the data environment just as they would in a real world environment However in the real world we are not just passive observers When examining and learning ab out a new ob ject we have the ability to manipulate b oth the ob ject itself and our surroundings In some cases the ability -

To Do Outline Phong Illumination Model Idea of Phong Illumination Phong Formula
To Do Foundations of Computer Graphics (Spring 2010) . Work on HW4 milestone CS 184, Lecture 18: Shading & Texture Mapping . Prepare for final push on HW 4, HW 5 http://inst.eecs.berkeley.edu/~cs184 Many slides from Greg Humphreys, UVA and Rosalee Wolfe, DePaul tutorial teaching texture mapping visually Chapter 11 in text book covers some portions Outline Phong Illumination Model . Brief discussion on Phong illumination model . Specular or glossy materials: highlights and Gouraud, Phong shading . Polished floors, glossy paint, whiteboards . For plastics highlight is color of light source (not object) . Texture Mapping (bulk of lecture) . For metals, highlight depends on surface color . Really, (blurred) reflections of light source These are key components of shading Roughness Idea of Phong Illumination Phong Formula . Find a simple way to create highlights that are view- I ()RE p dependent and happen at about the right place R . Not physically based -L . Use dot product (cosine) of eye and reflection of E light direction about surface normal . Alternatively, dot product of half angle and normal . Raise cosine lobe to some power to control sharpness or roughness R ? R LLNN 2( ) 1 Alternative: Half-Angle (Blinn-Phong) Flat vs. Gouraud Shading I ()NH p N H glShadeModel(GL_FLAT) glShadeModel(GL_SMOOTH) Flat - Determine that each face has a single normal, and color the entire face a single value, based on that normal. In practice, both diffuse and specular Gouraud – Determine the color at each vertex, using the normal at components for most materials that vertex, and interpolate linearly for pixels between vertex locations. Gouraud Shading – Details Gouraud and Errors I1221()()yys Iyy s Ia yy12 . -

Flat Shading
Shading Reading: Angel Ch.6 What is “Shading”? So far we have built 3D models with polygons and rendered them so that each polygon has a uniform colour: - results in a ‘flat’ 2D appearance rather than 3D - implicitly assumed that the surface is lit such that to the viewer it appears uniform ‘Shading’ gives the surface its 3D appearance - under natural illumination surfaces give a variation in colour ‘shading’ across the surface - the amount of reflected light varies depends on: • the angle between the surface and the viewer • angle between the illumination source and surface • surface material properties (colour/roughness…) Shading is essential to generate realistic images of 3D scenes Realistic Shading The goal is to render scenes that appear as realistic as photographs of real scenes This requires simulation of the physical processes of image formation - accurate modeling of physics results in highly realistic images - accurate modeling is computationally expensive (not real-time) - to achieve a real-time graphics pipeline performance we must compromise between physical accuracy and computational cost To model shading requires: (1) Model of light source (2) Model of surface reflection Physically accurate modelling of shading requires a global analysis of the scene and illumination to account for surface reflection between surfaces/shadowing/ transparency etc. Fast shading calculation considers only local analysis based on: - material properties/surface geometry/light source position & properties Physics of Image Formation Consider the -

Real Time Lighting Tutorial
Tutorial 11: Real-Time Lighting A Summary The graphical applications you have been making so far have been very basic, with only texture maps to add realisim. Lighting effects have long been used to enhance the realism in games, and the following two tutorials will show you how to perform such lighting calculations in your shaders. New Concepts Vertex Normals, Normal Matrix, Flat Shading, Gourard Shading, Blinn-Phong Shading, Specularity, Lambert's Cosine Law Normals In order to be able to simulate the effects of light bouncing off the surfaces of the meshes in our games, we must first be able to determine the direction the surfaces are facing in. We do this using the normal of each surface. This is a normalised direction vector, pointing away from the surface, like so: Like everything else related to geometry rendering, normals are vertex attributes, and so are interpolated in the vertex shader, forming a surface normal for each fragment in the scene. 1 Calculating Normals Nearly all of the geometry you'll render on screen is made up of triangles, and it is fortunately very easy to calculate the surface normal of a triangle. The cross product of two vectors a and b produces a vector that is orthogonal to both a and b, ideal to use as a surface normal: cross(V ector3a; V ector3b) = V ector3(aybz − azby; azbx − axbz; axby − aybx) But which two vectors will result in the correct normal for a triangle? Simple - we pick one of the triangle's vertices, and the two direction vectors that point towards the other two triangle vertices can be used to generate the normal for a triangle by cross product. -

Shading & Texturing
Shading & Texturing Overview Scan conversion Figure out which pixels to draw/fill Shading Determine a color for each filled pixel Texture Mapping Describe shading variation within polygon interiors Shading How do we choose a color for each filled pixel? Each illumination calculation for a ray from the eyepoint through the view plane provides a radiance sample How do we choose where to place samples? How do we filter samples to reconstruct image? Emphasis on methods that can be implemented in hardware Ray Casting Simplest shading approach is to perform independent lighting calculation for every pixel When is this unnecessary? I I K I (K (N L )I K (V R )n I ) E A AL i D i i S i i Polygon Shading Can take advantage of spatial coherence Illumination calculations for pixels covered by same primitive are related to each other Algorithms: Flat Shading Gouraud Shading Phong Shading Flat Shading What if a faceted object is illuminated only by directional light sources and is either diffuse or viewed from infinitely far away Flat Shading One illumination calculation per polygon Assign all pixels inside each polygon the same color N Flat Shading Objects look like they are composed of polygons OK for polyhedral objects Not so good for ones with smooth surfaces Gouraud Shading What if smooth surface is represented by polygonal mesh with a normal at each vertex? I I K I (K (N L )I K (V R )n I ) E A AL i D i i S i i Gouraud Shading Step 1: One lighting calculation per vertex Assign pixels inside polygon by interpolating -

Professional Papervision3d
Professional Papervision3D Part I: Getting Started Chapter 1: Understanding Flash3D ..................................................................3 Chapter 2: Getting Started With Papervision3D .............................................33 Chapter 3: Rezzing Primitives........................................................................75 Chapter 4: Adding Materials ...................................................................... 127 Part II: Working with Models and Data Chapter 5: Creating 3D Models .................................................................. 173 Chapter 6: Working with Particle Systems ..................................................221 Chapter 7: Geocoding, XML, and Databases ............................................... 253 Chapter 8: Gliding on AIR........................................................................... 285 Part III: Building Games and Websites Chapter 9: Incorporating 3D Physics .......................................................... 321 Chapter 10: Building 3D Games for Wii .......................................................365 Chapter 11: Integrating the Flash Media Server ..........................................417 Chapter 12: Developing 3D Websites ......................................................... 459 Part IV: Extending PV3D and Beyond Chapter 13: Making 3D Movies ..................................................................491 Chapter 14: Taking Virtual Tours ................................................................ 521 Chapter 15: Adding -

Direct Volume Rendering with Shading Via Three-Dimensional
Direct Volume Rendering with Shading via Three-Dimensional Textures Allen Van Gelder Kwansik Kim University of California, Santa Cruz Abstract comfortable stereographic viewing,do not degrade the performance. A new and easy-to-implement method for direct volume rendering A stereo interface has been implemented. that uses 3D texture maps for acceleration, and incorporates Voltx is robust in the sense that it is able to produce images directional lighting, is described. The implementation, called of good quality even though the transfer function has high Voltx, produces high-quality images at nearly interactive speeds on frequencies or discontinuities. Also, rotations of the volume do workstations with hardware support for three-dimensional texture not introduce artifacts, and perspective projections do not degrade maps. Previously reported methods did not incorporate a light the performance. All of these problems were reported for LL by model, and did not address issues of multiple texture maps for Lacroute and Levoy [LL94]. Their paper suggests ways to get large volumes. Our research shows that these extensions impact around some of the problems. performance by about a factor of ten. Voltx supports orthographic, Some limitations of Voltx are the restriction to rectilinear perspective, and stereo views. This paper describes the theory and volumes, the need to rede®ne 3D texture maps wheneverthe volume implementation of this technique, and compares it to the shear-warp is viewed from a new rotation, and the fact that color, not data, is factorization approach. loaded into texture memory. The ®rst limitation may be inherent A rectilinear data set is converted into a three-dimensional texture in the method.