Continuous Functions
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Section 8.8: Improper Integrals
Section 8.8: Improper Integrals One of the main applications of integrals is to compute the areas under curves, as you know. A geometric question. But there are some geometric questions which we do not yet know how to do by calculus, even though they appear to have the same form. Consider the curve y = 1=x2. We can ask, what is the area of the region under the curve and right of the line x = 1? We have no reason to believe this area is finite, but let's ask. Now no integral will compute this{we have to integrate over a bounded interval. Nonetheless, we don't want to throw up our hands. So note that b 2 b Z (1=x )dx = ( 1=x) 1 = 1 1=b: 1 − j − In other words, as b gets larger and larger, the area under the curve and above [1; b] gets larger and larger; but note that it gets closer and closer to 1. Thus, our intuition tells us that the area of the region we're interested in is exactly 1. More formally: lim 1 1=b = 1: b − !1 We can rewrite that as b 2 lim Z (1=x )dx: b !1 1 Indeed, in general, if we want to compute the area under y = f(x) and right of the line x = a, we are computing b lim Z f(x)dx: b !1 a ASK: Does this limit always exist? Give some situations where it does not exist. They'll give something that blows up. -

Notes on Calculus II Integral Calculus Miguel A. Lerma
Notes on Calculus II Integral Calculus Miguel A. Lerma November 22, 2002 Contents Introduction 5 Chapter 1. Integrals 6 1.1. Areas and Distances. The Definite Integral 6 1.2. The Evaluation Theorem 11 1.3. The Fundamental Theorem of Calculus 14 1.4. The Substitution Rule 16 1.5. Integration by Parts 21 1.6. Trigonometric Integrals and Trigonometric Substitutions 26 1.7. Partial Fractions 32 1.8. Integration using Tables and CAS 39 1.9. Numerical Integration 41 1.10. Improper Integrals 46 Chapter 2. Applications of Integration 50 2.1. More about Areas 50 2.2. Volumes 52 2.3. Arc Length, Parametric Curves 57 2.4. Average Value of a Function (Mean Value Theorem) 61 2.5. Applications to Physics and Engineering 63 2.6. Probability 69 Chapter 3. Differential Equations 74 3.1. Differential Equations and Separable Equations 74 3.2. Directional Fields and Euler’s Method 78 3.3. Exponential Growth and Decay 80 Chapter 4. Infinite Sequences and Series 83 4.1. Sequences 83 4.2. Series 88 4.3. The Integral and Comparison Tests 92 4.4. Other Convergence Tests 96 4.5. Power Series 98 4.6. Representation of Functions as Power Series 100 4.7. Taylor and MacLaurin Series 103 3 CONTENTS 4 4.8. Applications of Taylor Polynomials 109 Appendix A. Hyperbolic Functions 113 A.1. Hyperbolic Functions 113 Appendix B. Various Formulas 118 B.1. Summation Formulas 118 Appendix C. Table of Integrals 119 Introduction These notes are intended to be a summary of the main ideas in course MATH 214-2: Integral Calculus. -

Two Fundamental Theorems About the Definite Integral
Two Fundamental Theorems about the Definite Integral These lecture notes develop the theorem Stewart calls The Fundamental Theorem of Calculus in section 5.3. The approach I use is slightly different than that used by Stewart, but is based on the same fundamental ideas. 1 The definite integral Recall that the expression b f(x) dx ∫a is called the definite integral of f(x) over the interval [a,b] and stands for the area underneath the curve y = f(x) over the interval [a,b] (with the understanding that areas above the x-axis are considered positive and the areas beneath the axis are considered negative). In today's lecture I am going to prove an important connection between the definite integral and the derivative and use that connection to compute the definite integral. The result that I am eventually going to prove sits at the end of a chain of earlier definitions and intermediate results. 2 Some important facts about continuous functions The first intermediate result we are going to have to prove along the way depends on some definitions and theorems concerning continuous functions. Here are those definitions and theorems. The definition of continuity A function f(x) is continuous at a point x = a if the following hold 1. f(a) exists 2. lim f(x) exists xœa 3. lim f(x) = f(a) xœa 1 A function f(x) is continuous in an interval [a,b] if it is continuous at every point in that interval. The extreme value theorem Let f(x) be a continuous function in an interval [a,b]. -
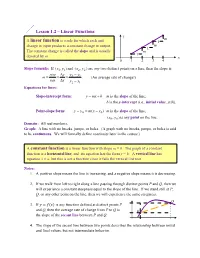
Lesson 1.2 – Linear Functions Y M a Linear Function Is a Rule for Which Each Unit 1 Change in Input Produces a Constant Change in Output
Lesson 1.2 – Linear Functions y m A linear function is a rule for which each unit 1 change in input produces a constant change in output. m 1 The constant change is called the slope and is usually m 1 denoted by m. x 0 1 2 3 4 Slope formula: If (x1, y1)and (x2 , y2 ) are any two distinct points on a line, then the slope is rise y y y m 2 1 . (An average rate of change!) run x x x 2 1 Equations for lines: Slope-intercept form: y mx b m is the slope of the line; b is the y-intercept (i.e., initial value, y(0)). Point-slope form: y y0 m(x x0 ) m is the slope of the line; (x0, y0 ) is any point on the line. Domain: All real numbers. Graph: A line with no breaks, jumps, or holes. (A graph with no breaks, jumps, or holes is said to be continuous. We will formally define continuity later in the course.) A constant function is a linear function with slope m = 0. The graph of a constant function is a horizontal line, and its equation has the form y = b. A vertical line has equation x = a, but this is not a function since it fails the vertical line test. Notes: 1. A positive slope means the line is increasing, and a negative slope means it is decreasing. 2. If we walk from left to right along a line passing through distinct points P and Q, then we will experience a constant steepness equal to the slope of the line. -

Lecture 13 Gradient Methods for Constrained Optimization
Lecture 13 Gradient Methods for Constrained Optimization October 16, 2008 Lecture 13 Outline • Gradient Projection Algorithm • Convergence Rate Convex Optimization 1 Lecture 13 Constrained Minimization minimize f(x) subject x ∈ X • Assumption 1: • The function f is convex and continuously differentiable over Rn • The set X is closed and convex ∗ • The optimal value f = infx∈Rn f(x) is finite • Gradient projection algorithm xk+1 = PX[xk − αk∇f(xk)] starting with x0 ∈ X. Convex Optimization 2 Lecture 13 Bounded Gradients Theorem 1 Let Assumption 1 hold, and suppose that the gradients are uniformly bounded over the set X. Then, the projection gradient method generates the sequence {xk} ⊂ X such that • When the constant stepsize αk ≡ α is used, we have 2 ∗ αL lim inf f(xk) ≤ f + k→∞ 2 P • When diminishing stepsize is used with k αk = +∞, we have ∗ lim inf f(xk) = f . k→∞ Proof: We use projection properties and the line of analysis similar to that of unconstrained method. HWK 6 Convex Optimization 3 Lecture 13 Lipschitz Gradients • Lipschitz Gradient Lemma For a differentiable convex function f with Lipschitz gradients, we have for all x, y ∈ Rn, 1 k∇f(x) − ∇f(y)k2 ≤ (∇f(x) − ∇f(y))T (x − y), L where L is a Lipschitz constant. • Theorem 2 Let Assumption 1 hold, and assume that the gradients of f are Lipschitz continuous over X. Suppose that the optimal solution ∗ set X is not empty. Then, for a constant stepsize αk ≡ α with 0 2 < α < L converges to an optimal point, i.e., ∗ ∗ ∗ lim kxk − x k = 0 for some x ∈ X . -

Calculus Terminology
AP Calculus BC Calculus Terminology Absolute Convergence Asymptote Continued Sum Absolute Maximum Average Rate of Change Continuous Function Absolute Minimum Average Value of a Function Continuously Differentiable Function Absolutely Convergent Axis of Rotation Converge Acceleration Boundary Value Problem Converge Absolutely Alternating Series Bounded Function Converge Conditionally Alternating Series Remainder Bounded Sequence Convergence Tests Alternating Series Test Bounds of Integration Convergent Sequence Analytic Methods Calculus Convergent Series Annulus Cartesian Form Critical Number Antiderivative of a Function Cavalieri’s Principle Critical Point Approximation by Differentials Center of Mass Formula Critical Value Arc Length of a Curve Centroid Curly d Area below a Curve Chain Rule Curve Area between Curves Comparison Test Curve Sketching Area of an Ellipse Concave Cusp Area of a Parabolic Segment Concave Down Cylindrical Shell Method Area under a Curve Concave Up Decreasing Function Area Using Parametric Equations Conditional Convergence Definite Integral Area Using Polar Coordinates Constant Term Definite Integral Rules Degenerate Divergent Series Function Operations Del Operator e Fundamental Theorem of Calculus Deleted Neighborhood Ellipsoid GLB Derivative End Behavior Global Maximum Derivative of a Power Series Essential Discontinuity Global Minimum Derivative Rules Explicit Differentiation Golden Spiral Difference Quotient Explicit Function Graphic Methods Differentiable Exponential Decay Greatest Lower Bound Differential -

The Infinite and Contradiction: a History of Mathematical Physics By
The infinite and contradiction: A history of mathematical physics by dialectical approach Ichiro Ueki January 18, 2021 Abstract The following hypothesis is proposed: \In mathematics, the contradiction involved in the de- velopment of human knowledge is included in the form of the infinite.” To prove this hypothesis, the author tries to find what sorts of the infinite in mathematics were used to represent the con- tradictions involved in some revolutions in mathematical physics, and concludes \the contradiction involved in mathematical description of motion was represented with the infinite within recursive (computable) set level by early Newtonian mechanics; and then the contradiction to describe discon- tinuous phenomena with continuous functions and contradictions about \ether" were represented with the infinite higher than the recursive set level, namely of arithmetical set level in second or- der arithmetic (ordinary mathematics), by mechanics of continuous bodies and field theory; and subsequently the contradiction appeared in macroscopic physics applied to microscopic phenomena were represented with the further higher infinite in third or higher order arithmetic (set-theoretic mathematics), by quantum mechanics". 1 Introduction Contradictions found in set theory from the end of the 19th century to the beginning of the 20th, gave a shock called \a crisis of mathematics" to the world of mathematicians. One of the contradictions was reported by B. Russel: \Let w be the class [set]1 of all classes which are not members of themselves. Then whatever class x may be, 'x is a w' is equivalent to 'x is not an x'. Hence, giving to x the value w, 'w is a w' is equivalent to 'w is not a w'."[52] Russel described the crisis in 1959: I was led to this contradiction by Cantor's proof that there is no greatest cardinal number. -

9 Power and Polynomial Functions
Arkansas Tech University MATH 2243: Business Calculus Dr. Marcel B. Finan 9 Power and Polynomial Functions A function f(x) is a power function of x if there is a constant k such that f(x) = kxn If n > 0, then we say that f(x) is proportional to the nth power of x: If n < 0 then f(x) is said to be inversely proportional to the nth power of x. We call k the constant of proportionality. Example 9.1 (a) The strength, S, of a beam is proportional to the square of its thickness, h: Write a formula for S in terms of h: (b) The gravitational force, F; between two bodies is inversely proportional to the square of the distance d between them. Write a formula for F in terms of d: Solution. 2 k (a) S = kh ; where k > 0: (b) F = d2 ; k > 0: A power function f(x) = kxn , with n a positive integer, is called a mono- mial function. A polynomial function is a sum of several monomial func- tions. Typically, a polynomial function is a function of the form n n−1 f(x) = anx + an−1x + ··· + a1x + a0; an 6= 0 where an; an−1; ··· ; a1; a0 are all real numbers, called the coefficients of f(x): The number n is a non-negative integer. It is called the degree of the polynomial. A polynomial of degree zero is just a constant function. A polynomial of degree one is a linear function, of degree two a quadratic function, etc. The number an is called the leading coefficient and a0 is called the constant term. -

Convergence Rates for Deterministic and Stochastic Subgradient
Convergence Rates for Deterministic and Stochastic Subgradient Methods Without Lipschitz Continuity Benjamin Grimmer∗ Abstract We extend the classic convergence rate theory for subgradient methods to apply to non-Lipschitz functions. For the deterministic projected subgradient method, we present a global O(1/√T ) convergence rate for any convex function which is locally Lipschitz around its minimizers. This approach is based on Shor’s classic subgradient analysis and implies generalizations of the standard convergence rates for gradient descent on functions with Lipschitz or H¨older continuous gradients. Further, we show a O(1/√T ) convergence rate for the stochastic projected subgradient method on convex functions with at most quadratic growth, which improves to O(1/T ) under either strong convexity or a weaker quadratic lower bound condition. 1 Introduction We consider the nonsmooth, convex optimization problem given by min f(x) x∈Q for some lower semicontinuous convex function f : Rd R and closed convex feasible → ∪{∞} region Q. We assume Q lies in the domain of f and that this problem has a nonempty set of minimizers X∗ (with minimum value denoted by f ∗). Further, we assume orthogonal projection onto Q is computationally tractable (which we denote by PQ( )). arXiv:1712.04104v3 [math.OC] 26 Feb 2018 Since f may be nondifferentiable, we weaken the notion of gradients to· subgradients. The set of all subgradients at some x Q (referred to as the subdifferential) is denoted by ∈ ∂f(x)= g Rd y Rd f(y) f(x)+ gT (y x) . { ∈ | ∀ ∈ ≥ − } We consider solving this problem via a (potentially stochastic) projected subgradient method. -

Polynomials.Pdf
POLYNOMIALS James T. Smith San Francisco State University For any real coefficients a0,a1,...,an with n $ 0 and an =' 0, the function p defined by setting n p(x) = a0 + a1 x + AAA + an x for all real x is called a real polynomial of degree n. Often, we write n = degree p and call an its leading coefficient. The constant function with value zero is regarded as a real polynomial of degree –1. For each n the set of all polynomials with degree # n is closed under addition, subtraction, and multiplication by scalars. The algebra of polynomials of degree # 0 —the constant functions—is the same as that of real num- bers, and you need not distinguish between those concepts. Polynomials of degrees 1 and 2 are called linear and quadratic. Polynomial multiplication Suppose f and g are nonzero polynomials of degrees m and n: m f (x) = a0 + a1 x + AAA + am x & am =' 0, n g(x) = b0 + b1 x + AAA + bn x & bn =' 0. Their product fg is a nonzero polynomial of degree m + n: m+n f (x) g(x) = a 0 b 0 + AAA + a m bn x & a m bn =' 0. From this you can deduce the cancellation law: if f, g, and h are polynomials, f =' 0, and fg = f h, then g = h. For then you have 0 = fg – f h = f ( g – h), hence g – h = 0. Note the analogy between this wording of the cancellation law and the corresponding fact about multiplication of numbers. One of the most useful results about integer multiplication is the unique factoriza- tion theorem: for every integer f > 1 there exist primes p1 ,..., pm and integers e1 em e1 ,...,em > 0 such that f = pp1 " m ; the set consisting of all pairs <pk , ek > is unique. -

Mean Value, Taylor, and All That
Mean Value, Taylor, and all that Ambar N. Sengupta Louisiana State University November 2009 Careful: Not proofread! Derivative Recall the definition of the derivative of a function f at a point p: f (w) − f (p) f 0(p) = lim (1) w!p w − p Derivative Thus, to say that f 0(p) = 3 means that if we take any neighborhood U of 3, say the interval (1; 5), then the ratio f (w) − f (p) w − p falls inside U when w is close enough to p, i.e. in some neighborhood of p. (Of course, we can’t let w be equal to p, because of the w − p in the denominator.) In particular, f (w) − f (p) > 0 if w is close enough to p, but 6= p. w − p Derivative So if f 0(p) = 3 then the ratio f (w) − f (p) w − p lies in (1; 5) when w is close enough to p, i.e. in some neighborhood of p, but not equal to p. Derivative So if f 0(p) = 3 then the ratio f (w) − f (p) w − p lies in (1; 5) when w is close enough to p, i.e. in some neighborhood of p, but not equal to p. In particular, f (w) − f (p) > 0 if w is close enough to p, but 6= p. w − p • when w > p, but near p, the value f (w) is > f (p). • when w < p, but near p, the value f (w) is < f (p). Derivative From f 0(p) = 3 we found that f (w) − f (p) > 0 if w is close enough to p, but 6= p. -

MATH 162: Calculus II Differentiation
MATH 162: Calculus II Framework for Mon., Jan. 29 Review of Differentiation and Integration Differentiation Definition of derivative f 0(x): f(x + h) − f(x) f(y) − f(x) lim or lim . h→0 h y→x y − x Differentiation rules: 1. Sum/Difference rule: If f, g are differentiable at x0, then 0 0 0 (f ± g) (x0) = f (x0) ± g (x0). 2. Product rule: If f, g are differentiable at x0, then 0 0 0 (fg) (x0) = f (x0)g(x0) + f(x0)g (x0). 3. Quotient rule: If f, g are differentiable at x0, and g(x0) 6= 0, then 0 0 0 f f (x0)g(x0) − f(x0)g (x0) (x0) = 2 . g [g(x0)] 4. Chain rule: If g is differentiable at x0, and f is differentiable at g(x0), then 0 0 0 (f ◦ g) (x0) = f (g(x0))g (x0). This rule may also be expressed as dy dy du = . dx x=x0 du u=u(x0) dx x=x0 Implicit differentiation is a consequence of the chain rule. For instance, if y is really dependent upon x (i.e., y = y(x)), and if u = y3, then d du du dy d (y3) = = = (y3)y0(x) = 3y2y0. dx dx dy dx dy Practice: Find d x d √ d , (x2 y), and [y cos(xy)]. dx y dx dx MATH 162—Framework for Mon., Jan. 29 Review of Differentiation and Integration Integration The definite integral • the area problem • Riemann sums • definition Fundamental Theorem of Calculus: R x I: Suppose f is continuous on [a, b].