Dynamics of Online Social Networks Cascading Phenomena and Collapse
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

An Exploratory Study of Global and Local Discourses on Social Media Regulation
Global Media Journal German Edition From the field An Exploratory Study of Global and Local Discourses on Social Media Regulation Andrej Školkay1 Abstract: This is a study of suggested approaches to social media regulation based on an explora- tory methodological approach. Its first aim is to provide an overview of the global and local debates and the main arguments and concerns, and second, to systematise this in order to construct taxon- omies. Despite its methodological limitations, the study provides new insights into this very rele- vant global and local policy debate. We found that there are trends in regulatory policymaking to- wards both innovative and radical approaches but also towards approaches of copying broadcast media regulation to the sphere of social media. In contrast, traditional self- and co-regulatory ap- proaches seem to have been, by and large, abandoned as the preferred regulatory approaches. The study discusses these regulatory approaches as presented in global and selected local, mostly Euro- pean and US discourses in three analytical groups based on the intensity of suggested regulatory intervention. Keywords: social media, regulation, hate speech, fake news, EU, USA, media policy, platforms Author information: Dr. Andrej Školkay is director of research at the School of Communication and Media, Bratislava, Slovakia. He has published widely on media and politics, especially on political communication, but also on ethics, media regulation, populism, and media law in Slovakia and abroad. His most recent book is Media Law in Slovakia (Kluwer Publishers, 2016). Dr. Školkay has been a leader of national research teams in the H2020 Projects COMPACT (CSA - 2017-2020), DEMOS (RIA - 2018-2021), FP7 Projects MEDIADEM (2010-2013) and ANTICORRP (2013-2017), as well as Media Plurality Monitor (2015). -

Minutes from City Commission Minutes From
DUNEDIN, FLORIDA MINUTES OF THE CITY COMMISSION WORK SESSION MARCH 17, 2020 9:00A.M. -12:30 P.M. Present: City Commission: Mayor Julie Ward Bujalsk1, V1ce-Mayor Heather Gracy, Commissioners, Deborah Kynes and Jeff Gow Commissioner Maureen "Moe" Freaney (Via Conference Call) Also Present. City Manager Jennifer K Bramley, Deputy C1ty Manager Doug Hutchens, City Attorney Thomas J. Trask, City Clerk Rebecca Schlichter, Finance Director Les Tyler, Commumty Development Planner II Frances Sharp, Economic & Housing Development!CRA Director Robert lronsm1th, Assistant D1rector of Public Works & Utilities Paul Stanek, Community Relations .TV Production Specialist Just1n Catacchio, Information Technology Services Division D1rector Michael Nagy, Parks and Recreation Director Vince Gizzi, Parks & Recreation Administration Supenntendent Lame Sheets, Community Center Program Coordinator Jorie Peterson, Fire Chief Jeffrey Parks, Deputy Fire Chief Erich Thiemann, Fire Marshal M1ke Handoga, Library Director Phyllis Gorshe and approximately five people. CALL TO ORDER 1 Mayor Bujalski called the Work Session to order at 9:00 a.m. City Attorney Trask explained for any action to take place at the Commission level 1t requ1res all meetings to be held in the Sunshine. It is his understanding Commissioner Freaney has recently been on a cruise and has self-quarantined as a d1rect result of the Coronavirus pandemic and the emergency it creates, she is attending this Commission Meeting by way of aud1o. The Attorney General has opmed on th1s m 1992 that so long as there is a quorum physically present at the meeting and so long as an emergency exists a Commissioner can attend the meeting and part1c1pate m the meeting by phone. -

Image and Self-Representation
Veszelszki, Ágnes (ELTE) Image and Self-representation Giving people the power to share and make the world more open and connected.1 1. Introduction The involvement of image information is commonly said to be an accessory of digital change (see: Schlobinski 2009: 6). Visuality has a much more important role in our days than it had in the earlier periods of communication history. Just have a look at the graphical user interface of computer programmes, the layout of web pages, texts full of smileys and the torrent of pictures shared on social networking pages. This paradigm shift in the wake of the Gutenberg Galaxy is termed by Gottfried Boehm as the “Iconic Turn” (Boehm 1994). With the spread of visual communication technologies, visual communication itself is getting more and more common, too (Nyíri 2003: 273). In fact, some speak about the omnipresence of pictures (“Omnipräsenz der Bilder”; Maar 2006). Images are not under the control of consciousness, they bypass our minds and influence our thinking and emotions through their suggestive power (Giulani 2006: 185). Profile pictures on social networking websites fall into a peculiar category. It’s an open secret that our photos uploaded to such websites are not only viewed by our friends and family members but also by our present or future employer. A British survey, which was carried out by the People Search website, polled almost one thousand HR managers asking them if they inspected their employee-to-be’s photos shared on the internet before contracting them. One third of the British managers said that they regularly viewed their colleagues’ photos and internet posts, and they found this method of gathering information quite important before hiring a new employee. -

Geographies of an Online Social Network
Geographies of an online social network Balázs Lengyel a,b, 1, Attila Varga c, Bence Ságvári a,d, Ákos Jakobi e, János Kertész f,g a International Business School Budapest, OSON Research Lab, Záhony utca 7, 1031 Budapest, Hungary b Hungarian Academy of Sciences, Centre for Economic and Regional Studies, Budaörsi út 45, 1112 Budapest, Hungary c The University of Arizona, School of Sociology, Tucson, AZ 85721-0027, USA d Hungarian Academy of Sciences, Centre for Social Sciences, Országház utca 30, 1014 Budapest, Hungary e Eötvös Loránd University, Department of Regional Science; Pázmány Péter sétány 1/C, 1117 Budapest, Hungary f Central European University, Centre for Network Science, Nádor utca 9, 1051 Budapest, Hungary g Budapest University of Technology and Economics, Institute of Physics, Budafoki út 8, 1111 Budapest, Hungary 1 Corresponding author: [email protected]. 1 Geographies of an online social network Abstract How is online social media activity structured in the geographical space? Recent studies have shown that in spite of earlier visions about the “death of distance”, physical proximity is still a major factor in social tie formation and maintenance in virtual social networks. Yet, it is unclear, what are the characteristics of the distance dependence in online social networks. In order to explore this issue the complete network of the former major Hungarian online social network is analyzed. We find that the distance dependence is weaker for the online social network ties than what was found earlier for phone communication networks. For a further analysis we introduced a coarser granularity: We identified the settlements with the nodes of a network and assigned two kinds of weights to the links between them. -

Ethnology of the Blackfeet. INSTITUTION Browning School District 9, Mont
DOCUMENT RESUME ED 060 971 RC 005 944 AUTHOR McLaughlin, G. R., Comp. TITLE Ethnology of the Blackfeet. INSTITUTION Browning School DiStrict 9, Mont. PUB DATE [7 NOTE 341p. EDRS PRICE MF-$0.65 HC-$13-16 DESCRIPTORS *American Indians; Anthologies; Anthropology; *Cultural Background; *Ethnic Studies; Ethnolcg ; *High School Students; History; *Instructional Materials; Mythology; Religion; Reservations (Indian); Sociology; Values IDENTIFIERS *Blackfeet ABSTRACT Compiled for use in Indian history courses at the high-school level, this document contains sections on thehistory, culture, religion, and myths and legends of theBlackfeet. A guide to the spoken Blackfeftt Indian language andexamples of the language with English translations are also provided, asis information on sign language and picture writing. The constitutionand by-laws for the Blackfeet Tribe, a glossary of terms, and abibliography of books, films, tapes, and maps are also included. (IS) U S DEPARTMENT OF HEALTH EDUCATION & WELFARE OFFICE OF EDUCATION THIS DOCUMENT HAS BEEN REPRO DUCED EXACTLY AS RECEIVED FROM THE PERSON OR ORGANIZATION ORIG INATING IT POINTS OF VIEW OR OPIN IONS STATED DO NOT NECESSARILY REPRESENT OFFICIAL OFFICE OF EOU CATION POSITION OR POLICY le TABLE OF CONTBTTS Introductio Acknowledgement-- Cover Page -- Pronunciation of Indian Names Chapter I - History A Generalized View The Early Hunters 7 8 The Foragers The Late Hunters - -------- ----- Culture of the Late Hunters - - - - ---------- --- ---- ---9 The plains Tribes -- ---- - ---- ------11 The BlaLkfeet -

Social Networking Service History
Social Networking Service A social networking service is an online service, platform, or site that focuses on building and reflecting of social networks or social relations among people, who, for example, share interests and/or activities. A social network service essentially consists of a representation of each user (often a profile), his/her social links, and a variety of additional services. Most social network services are web based and provide means for users to interact over the Internet, such as e-mail and instant messaging. Online community services are sometimes considered as a social network service, though in a broader sense, social network service usually means an individual-centered service whereas online community services are group-centered. Social networking sites allow users to share ideas, activities, events, and interests within their individual networks. The main types of social networking services are those which contain category places (such as former school year or classmates), means to connect with friends (usually with self- description pages) and a recommendation system linked to trust. Popular methods now combine many of these, with Facebook and Twitter widely used worldwide, Nexopia (mostly in Canada); Bebo, VKontakte, Hi5, Hyves (mostly in The Netherlands), Draugiem.lv (mostly in Latvia), StudiVZ (mostly in Germany), iWiW (mostly in Hungary), Tuenti (mostly in Spain), Nasza-Klasa (mostly in Poland), Decayenne, Tagged, XING, Badoo and Skyrock in parts of Europe; Orkut and Hi5 in South America and Central America; and Mixi, Multiply, Orkut, Wretch, renren and Cyworld in Asia and the Pacific Islands and LinkedIn and Orkut are very popular in India. -

Interim Response
Monday, June 1, 2020 +1:rrr·zrw FBI is doing a very good iob here toniaht at SIOC - very good 11:31 PM synch up with our team (b) ( 5) Thursday, June 4, 2020 +1:rrr·zrw I really appreciated your remarks today at the press conference. 4:34 PM Thank you. Me Thanks Seth. 4:34 PM Saturday, June 6, 2020 +1·s1r:rrr As you think about your remarks for tomorrow, I encourage you to 9:18AM Me Thanks you, Seth. 9:21 AM Sunday, June 7, 2020 +1 :rrr·zrw 11:01 AM That was great! DAG and Ijust watched. Page 5 00678-00010 Wednesday, March 18, 2020 +1 rWffll':'f!!T! ■ POTUS meeting on (b)(5}., (b)(5) scheduled for tom . 3:32 PM Do you want to come to DOJ first or go direct to WH at 4:00? Me I will probably come in. 3:32 PM +1 rWffll':'f!!T! ■ Roger. Let me know when at some point so I can alert folks. 3:33 PM Me I'll come in at 3:34 PM About 1pm +1 rWffll':'f!!T! ■ Sounds good. 3:37 PM Sunday, March 22, 2020 9:17 AM +1 ll?if?!'fW:Wf ■ And these are the talking points on it we have at the moment: 9:18AM Page 7 00678-00020 Tuesday, March 24, 2020 +1 rWffll':'f!!T! ■ 9:28AM +1 ll?if?!'fW:Wf ■ Here is the number (b) (6) , and then you have to enter 1:04 PM am as a participant code. +1 ll?if?!'fW:Wf ■ Azar direct cell is (b) (6) I'm still working on the email. -
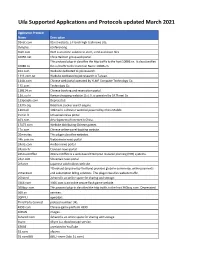
3000 Applications
Uila Supported Applications and Protocols updated March 2021 Application Protocol Name Description 01net.com 05001net plus website, is a Japanese a French embedded high-tech smartphonenews site. application dedicated to audio- 050 plus conferencing. 0zz0.com 0zz0 is an online solution to store, send and share files 10050.net China Railcom group web portal. This protocol plug-in classifies the http traffic to the host 10086.cn. It also classifies 10086.cn the ssl traffic to the Common Name 10086.cn. 104.com Web site dedicated to job research. 1111.com.tw Website dedicated to job research in Taiwan. 114la.com Chinese cloudweb portal storing operated system byof theYLMF 115 Computer website. TechnologyIt is operated Co. by YLMF Computer 115.com Technology Co. 118114.cn Chinese booking and reservation portal. 11st.co.kr ThisKorean protocol shopping plug-in website classifies 11st. the It ishttp operated traffic toby the SK hostPlanet 123people.com. Co. 123people.com Deprecated. 1337x.org Bittorrent tracker search engine 139mail 139mail is a chinese webmail powered by China Mobile. 15min.lt ChineseLithuanian web news portal portal 163. It is operated by NetEase, a company which pioneered the 163.com development of Internet in China. 17173.com Website distributing Chinese games. 17u.com 20Chinese minutes online is a travelfree, daily booking newspaper website. available in France, Spain and Switzerland. 20minutes This plugin classifies websites. 24h.com.vn Vietnamese news portal 24ora.com Aruban news portal 24sata.hr Croatian news portal 24SevenOffice 24SevenOffice is a web-based Enterprise resource planning (ERP) systems. 24ur.com Slovenian news portal 2ch.net Japanese adult videos web site 2Checkout (acquired by Verifone) provides global e-commerce, online payments 2Checkout and subscription billing solutions. -

Builsing CEE's Future Fabric
Outside in One new message Health check Intelligent life The rise and rise of public-to- Is social media really the Taking the temperature How Russia’s “innovation private equity deals saviour of business? of pharma in CEE city” will inspire the region Transform Issue 6/Autumn 2010 Insight for CEE’s business leaders Bridging the gap Special report: Building CEE’s future fabric Adviser of the Year to Private Equity in Central & Eastern Europe www.pwc.com/cee/private-equity unquote” has named PricewaterhouseCoopers For more information please contact: Adviser of the Year to the Private Equity CEE Private Equity Leader industry in Central & Eastern Europe. Mike Wilder Tel: +48 22 523 4413 The unquote” CEE Private Equity Awards [email protected] recognise excellence in the CEE private equity Czech Republic market. In a highly challenging environment over Miroslav Bratrych the past year, we were among a few select firms Tel: +420 251 15 2084 that still managed to achieve above-par [email protected] success. Poland Joanna Simonowicz PricewaterhouseCoopers helps more private Tel: +48 22 523 4213 equity houses to realise the unique investment [email protected] opportunities in Central & Eastern Europe than Russia any other adviser in the region. Jonathan Thornton Tel: +7 495 232 5711 [email protected] © 2010 PricewaterhouseCoopers. All rights reserved. “PricewaterhouseCoopers” refers to the network of member firms of PricewaterhouseCoopers International Limited, each of which is a separate and independent legal entity. FROM THE CEO Brave new world As trusted advisers to leading businesses across the globe, we at PwC often experience first hand the game- changing events of the corporate world. -

SOCIAL MEDIA MAP 2014 Evolving Landscape
A Snapshot of the SOCIAL MEDIA MAP 2014 Evolving Landscape SOCIAL NETWORKS PHOTO SHARING SOCIAL COMMERCE VIDEO SHARING CONTENT DISCOVERY facebook pinterest houzz youtube & CURATION google plus picasa groupon vimeo digg path tinypic google oers dailymotion INTERNATIONAL SOCIAL buzzfeed meetup snapchat saveology vevo NETWORKS squidoo tagged photobucket scoutmob vox vk addthis gather pingram livingsocial blip.tv badoo sharethis classmates pheed plumdistrict videolla odnoklassniki.ru reddit flickr polyvore vine skyrock blog lovin’ kaptur yipit ptch sina weibo fark fotolog gilt city telly PROFESSIONAL SOCIAL qzone stumbleupon imgur linkedin studivz diigo instagram scribd 51 SOCIAL GAMING dzone fotki SOCIAL Q&A docstoc iwiw.hu zynga google sites quora issuu hyves.nl the sims social individurls answers zimbra migente PRIVATE SOCIAL NETWORKS habbo contentgems stack exchange plaxo cyworld ning second life scoop.it yahoo! answers slideshare cloob yammer xbox live feedly wiki answers xing mixi.jp hall smallworlds trapit allexperts doximity renren convo imvu post planner gosoapbox naymz orkut salesforce chatter iflow PRODUCT/COMPANY answerbag protopage viadeo glassboard REVIEWS doc2doc swabr ask.com symbaloo MICROBLOGGING yelp communispace spring.me twitter angie's list blurtit E-COMMERCE PLATFORMS tumblr bizrate fluther shopify SOCIAL RECRUITING disqus epinions volution indeed plurk consumersearch WIKIS ecwild freelancer storify insiderpages wikipedia nexternal glassdoor PODCASTING consumerreports tv tropes graphite customer lobby wanelo elance LOCATION-BASED -

Facebook on Windows
Introduction to browser based Facebook Clarke Walker [email protected] Computer Learning Center of Ewing Welcome and Introductions Instructor Coach Students What operating system do you use? Do you have a Facebook account? What are your goals today? Course Specifics This course is an: Introduction This course is an introductory level course. Browser based Facebook can be accessed various ways. For this course we will be examining accessing Facebook using an Internet browser. Browsers like Internet Explorer, Firefox, Chrome and Safari. Desktop We will be using desktop Windows but the material should be suitable for any desktop environment. Course Purpose Purpose: Our goal is to make you comfortable with starting your journey with Face- book. What is Facebook Facebook.com is a social networking service. A social networking service is a platform to build social networks or social relations among people who, for example, share interests, activities, backgrounds, or real-life connections. A social network service consists of a representation of each user (often a profile), his/her social links, and a variety of additional services. Most social network services are web-based and provide means for users to in- teract over the Internet, such as e-mail and instant messaging. On- line community services are sometimes considered as a social net- work service, though in a broader sense, social network service usually means an individual-centered service whereas online com- munity services are group-centered. Social networking sites allow users to share ideas, pictures, posts, activities, events, and inter- ests with people in their network. What is Facebook Facebook.com is a social networking service. -

Social Network Services and Libraries
Original Research Article http://doi.org/10.18231/j.ijlsit.2019.003 Social network services and Libraries Somvir1*, Sudha Kaushik2 1,2Librarian, 1Ganga Institute of Technology and Management, 2P.D.M. University, Bahadurgarh, Haryana, Jhajjar, Haryana, India *Corresponding Author: Somvir Email: [email protected] Abstract Online Social Networks and Blogs are two leading web 2.0 technologies that can be adapted as a part of online services in the libraries. The history of social network service providers is discussed. The authors highlight the basic structure, additional features and the new emerging trends in the field of social networking services. In this paper author review the different impact on the society of the social network sites. Different types of domains are working for social networking. These networks can also be used for information distribution. The new generation users can get the library services at their own space and time by the libraries profile on these networks. To improve the status of Library and LIS professionals in the society in today’s busy digital era, social networking is one of the best media, because most of internet users are frequently using the social networking sites. And it is the best way of marketing of library services as well as strengthen the Library and LIS Profession and Professionals. A lot of libraries are using this for marketing of library services, promoting events, books reviews, users support, CAS, SDI, reference desk, library consortia etc. The merits and demerits of these social networking tools are also mentioned. Keywords: Social networking, Emerging trends, Social impact, Marketing of library services.